基于改進(jìn)螢火蟲算法的小波神經(jīng)網(wǎng)絡(luò)短期負(fù)荷預(yù)測(cè)方法*

劉 丹，張騰飛

(南京郵電大學(xué) 自動(dòng)化學(xué)院，江蘇 南京 210023)

?

基于改進(jìn)螢火蟲算法的小波神經(jīng)網(wǎng)絡(luò)短期負(fù)荷預(yù)測(cè)方法*

劉 丹，張騰飛

(南京郵電大學(xué) 自動(dòng)化學(xué)院，江蘇 南京 210023)

傳統(tǒng)的小波神經(jīng)網(wǎng)絡(luò)以梯度下降法訓(xùn)練網(wǎng)絡(luò)，而梯度下降法易導(dǎo)致網(wǎng)絡(luò)出現(xiàn)收斂早熟、陷入局部極小等問(wèn)題，影響網(wǎng)絡(luò)訓(xùn)練的精度。文章將螢火蟲算法用于訓(xùn)練小波神經(jīng)網(wǎng)絡(luò)，在全局內(nèi)搜尋網(wǎng)絡(luò)的最優(yōu)參數(shù)。為了提高螢火蟲算法參數(shù)尋優(yōu)的能力，在訓(xùn)練過(guò)程中自適應(yīng)調(diào)節(jié)γ值。同時(shí)利用高斯變異來(lái)提高螢火蟲個(gè)體的活性，在保證收斂速度的同時(shí)避免算法陷入局部極小。將優(yōu)化后的小波神經(jīng)網(wǎng)絡(luò)用于短期負(fù)荷預(yù)測(cè)，實(shí)驗(yàn)證明改進(jìn)后的預(yù)測(cè)模型非線性擬合能力較強(qiáng)、預(yù)測(cè)精度較高。

小波神經(jīng)網(wǎng)絡(luò)；螢火蟲算法；負(fù)荷預(yù)測(cè)；全局尋優(yōu)

0 引言

短期負(fù)荷預(yù)測(cè)主要是預(yù)報(bào)未來(lái)24小時(shí)至幾天內(nèi)的系統(tǒng)負(fù)荷[1]。精確的負(fù)荷預(yù)測(cè)有助于合理安排機(jī)組的檢修計(jì)劃以及規(guī)劃未來(lái)發(fā)電機(jī)組的安裝，對(duì)社會(huì)生活和經(jīng)濟(jì)發(fā)展意義重大。從經(jīng)典的單耗法、彈性系數(shù)法到當(dāng)前的灰色預(yù)測(cè)法、神經(jīng)網(wǎng)絡(luò)法等，負(fù)荷預(yù)測(cè)技術(shù)在不斷進(jìn)步。其中，神經(jīng)網(wǎng)絡(luò)和小波分析法的優(yōu)勢(shì)較為突出，兩者相結(jié)合得到的小波神經(jīng)網(wǎng)絡(luò)常用于負(fù)荷預(yù)測(cè)。但是小波神經(jīng)網(wǎng)絡(luò)訓(xùn)練常采用梯度下降法，造成網(wǎng)絡(luò)易陷入局部極小，收斂速度慢[2-3]。

螢火蟲算法(Firefly Algorithm，F(xiàn)A)是一種基于群體搜索的仿生智能優(yōu)化算法，算法在尋優(yōu)精度和收斂速度方面很有優(yōu)勢(shì)[4]。本文采用螢火蟲算法訓(xùn)練小波神經(jīng)網(wǎng)絡(luò)，在訓(xùn)練過(guò)程中適時(shí)調(diào)節(jié)其參數(shù)γ值使得算法在全局內(nèi)有較強(qiáng)的搜索能力。同時(shí)對(duì)最優(yōu)螢火蟲個(gè)體進(jìn)行高斯變異，有利于螢火蟲個(gè)體跳離局部極小，保證網(wǎng)絡(luò)的收斂速度。最后用改進(jìn)后的螢火蟲算法優(yōu)化小波網(wǎng)絡(luò)的所有參數(shù)并進(jìn)行短期負(fù)荷預(yù)測(cè)，實(shí)驗(yàn)結(jié)果表明所提出的預(yù)測(cè)模型具有更好的收斂速度和預(yù)測(cè)精度。

1 小波神經(jīng)網(wǎng)絡(luò)模型

小波神經(jīng)網(wǎng)絡(luò)通常使用小波或尺度函數(shù)作為網(wǎng)絡(luò)的激活函數(shù)，其網(wǎng)絡(luò)結(jié)構(gòu)如圖1所示。

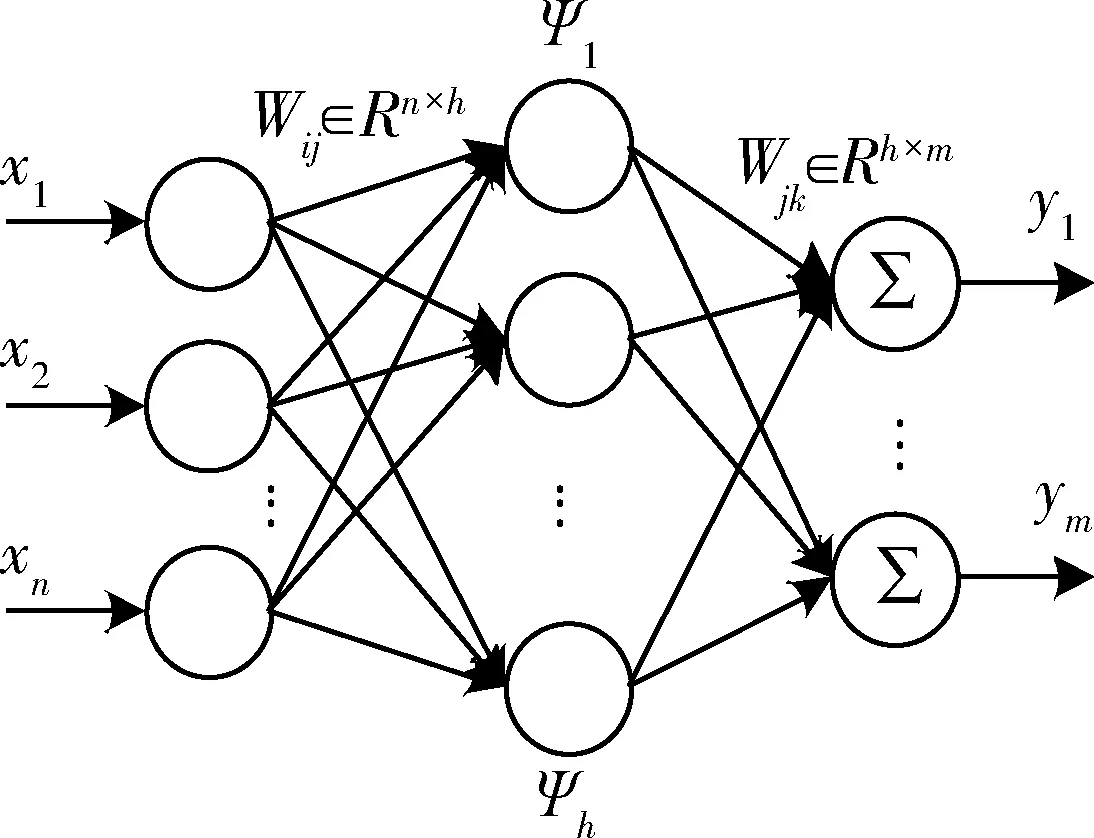
圖1 小波神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)

圖中X=(x1,x2,…,xn)為小波神經(jīng)網(wǎng)絡(luò)的輸入向量,Y=(y1,y2,…,ym)為網(wǎng)絡(luò)的輸出向量。隱含層共h個(gè)神經(jīng)元，其中Ψj為隱含層第j個(gè)神經(jīng)元的小波函數(shù)，其伸縮、平移系數(shù)分別為aj和bj。Wij為輸入層第i個(gè)神經(jīng)元與隱含層第j個(gè)神經(jīng)元之間的連接權(quán)值，Wjk為隱含層第j個(gè)神經(jīng)元與輸出層第k個(gè)神經(jīng)元的連接權(quán)值。其中隱層小波神經(jīng)元采用Mexican Hat小波函數(shù)，輸出層節(jié)點(diǎn)采用Sigmoid函數(shù)。小波神經(jīng)網(wǎng)絡(luò)隱含層第j(j=1,2,…,h)個(gè)小波神經(jīng)元輸入為：

(1)

隱含層第j個(gè)神經(jīng)元的輸出為：

(2)

輸出層第k(k=1,2,…,m)個(gè)神經(jīng)元的輸出為：

(3)

2 基于改進(jìn)螢火蟲算法的小波神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型

2.1 螢火蟲算法基本原理

螢火蟲算法中所有螢火蟲都具有一個(gè)由被優(yōu)化問(wèn)題決定的適應(yīng)度值。適應(yīng)度值越佳，螢火蟲亮度越強(qiáng)。隨著迭代過(guò)程的進(jìn)行，所有螢火蟲不斷向比自己更亮的螢火蟲靠近，最終大多數(shù)螢火蟲會(huì)聚集在最亮螢火蟲附近，最亮螢火蟲的位置就是問(wèn)題的最優(yōu)解[5]。

從數(shù)學(xué)角度對(duì)螢火蟲算法描述如下：

螢火蟲的相對(duì)熒光亮度：

I=I0×e-γrij

(4)

其中，I0為螢火蟲所處位置的熒光亮度；γ為光強(qiáng)吸收系數(shù)；rij為螢火蟲i與j之間的空間距離。

螢火蟲的吸引度為：

(5)

其中，β0表示最大吸引度因子，即最大熒光亮度處位置的吸引度大小。

螢火蟲i被螢火蟲j吸引移動(dòng)的位置更新公式：

xi(t+1)=xi+β×(xj-xi)+α×(rand-0.5)

(6)

其中，xi、xj分別為螢火蟲i和j所處的空間位置；α為步長(zhǎng)因子，取[0，1]上的常數(shù)；rand為[0，1]上服從均勻分布的隨機(jī)因子。

2.2 螢火蟲改進(jìn)算法

一般情況下，參數(shù)γ取1。當(dāng)求解空間較大時(shí)，螢火蟲之間的相對(duì)距離較大，式(5)中的rij會(huì)變大，β將趨向0。螢火蟲i則不會(huì)向較優(yōu)個(gè)體靠近，而是隨機(jī)更新位置。文獻(xiàn)[6]根據(jù)多次實(shí)驗(yàn)總結(jié)出：當(dāng)γr2在區(qū)間[0.04,4]時(shí)，e-γr2有較好的調(diào)節(jié)效果。

因此，當(dāng)群體距離較大時(shí)應(yīng)減小γ使γ0為0.04。當(dāng)螢火蟲群體距離較小時(shí)應(yīng)增大γ使得γ0為4。這樣保證e-γr2始終在特定范圍內(nèi)，從而保證螢火蟲群體間具有足夠吸引力，算法在全局內(nèi)有較強(qiáng)的搜索能力。

在傳統(tǒng)螢火蟲算法中，每一代最優(yōu)個(gè)體沒(méi)有作相應(yīng)處理，導(dǎo)致最優(yōu)個(gè)體進(jìn)化停滯，不利于算法的進(jìn)一步收斂。由文獻(xiàn)[7]可知，高斯變異具有較強(qiáng)的局部開發(fā)能力，因此采用高斯算子對(duì)最優(yōu)個(gè)體進(jìn)行變異，給每次迭代得到的最優(yōu)個(gè)體加上一個(gè)服從高斯分布的隨機(jī)擾動(dòng)項(xiàng)，如下：

(7)

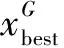
最后比較變異前后螢火蟲適應(yīng)度值的大小，取兩者中適應(yīng)度值較佳的個(gè)體為本次迭代的螢火蟲最優(yōu)個(gè)體xbest。

2.3 小波神經(jīng)網(wǎng)絡(luò)負(fù)荷預(yù)測(cè)模型

由于負(fù)荷工作日和休息日具有不同的周期性，需要分開建模。同時(shí)對(duì)短期負(fù)荷預(yù)測(cè)影響最大的就是溫度狀況[8]。因此預(yù)測(cè)某個(gè)工作日t時(shí)刻的負(fù)荷，小波網(wǎng)絡(luò)的輸入應(yīng)為預(yù)測(cè)日前一周t時(shí)刻、預(yù)測(cè)日前一日t-1時(shí)刻、預(yù)測(cè)日前一日t時(shí)刻、預(yù)測(cè)日t-2時(shí)刻、預(yù)測(cè)日t-1時(shí)刻的負(fù)荷和預(yù)測(cè)日前一周、預(yù)測(cè)日的平均溫度。輸出為預(yù)測(cè)日t時(shí)刻實(shí)際的負(fù)荷。

模型確定后，利用改進(jìn)的螢火蟲算法訓(xùn)練小波神經(jīng)網(wǎng)絡(luò)，將網(wǎng)絡(luò)的訓(xùn)練輸出負(fù)荷與實(shí)際負(fù)荷的誤差作為算法的適應(yīng)度值。具體步驟如下：

(1)根據(jù)學(xué)習(xí)樣本的輸入和輸出要求確定小波神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)。

(2)初始化螢火蟲種群，設(shè)定相應(yīng)的群體大小。種群中每個(gè)個(gè)體都包含了神經(jīng)網(wǎng)絡(luò)需要優(yōu)化的所有伸縮、平移系數(shù)以及連接權(quán)值。

(3)根據(jù)每個(gè)個(gè)體包含的網(wǎng)絡(luò)參數(shù)值計(jì)算對(duì)應(yīng)的適應(yīng)度值，其值越小，螢火蟲的亮度越大，其值越優(yōu)。

(4)根據(jù)改進(jìn)的螢火蟲算法迭代更新種群，搜尋最優(yōu)螢火蟲個(gè)體。

(5)將最優(yōu)個(gè)體中的參數(shù)值代入小波神經(jīng)網(wǎng)絡(luò)訓(xùn)練，并用測(cè)試數(shù)據(jù)進(jìn)行驗(yàn)證。

3 實(shí)驗(yàn)結(jié)果與分析

本文的訓(xùn)練樣本取自某地區(qū)5～7月份工作日24個(gè)時(shí)刻的實(shí)測(cè)數(shù)據(jù)，而測(cè)試數(shù)據(jù)為第二年6月份工作日24個(gè)時(shí)刻的實(shí)測(cè)數(shù)據(jù)。

為了驗(yàn)證改進(jìn)神經(jīng)網(wǎng)絡(luò)在預(yù)測(cè)方面的優(yōu)越性，將本文提出的預(yù)測(cè)模型(GFAWNN)與RBF神經(jīng)網(wǎng)絡(luò)、基于梯度下降法的小波神經(jīng)網(wǎng)絡(luò)(WNN)、基于螢火蟲算法的小波神經(jīng)網(wǎng)絡(luò)(FAWNN)進(jìn)行仿真結(jié)果對(duì)比。

觀察4種神經(jīng)網(wǎng)絡(luò)對(duì)第二年6月份所有工作日12：00這個(gè)時(shí)刻的負(fù)荷預(yù)測(cè)情況，如圖2所示。橫坐標(biāo)為30個(gè)測(cè)試樣本序列，縱坐標(biāo)為對(duì)應(yīng)樣本的負(fù)荷預(yù)測(cè)結(jié)果，黑色*線表示實(shí)際負(fù)荷值曲線。由圖可明顯看出，GFAWNN神經(jīng)網(wǎng)絡(luò)的擬合度最高，預(yù)測(cè)結(jié)果最佳，F(xiàn)AWNN網(wǎng)絡(luò)的預(yù)測(cè)效果次之，RBF預(yù)測(cè)效果最差。

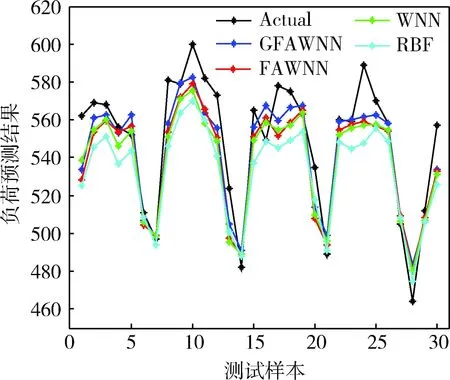
圖2 4種神經(jīng)網(wǎng)絡(luò)的短期負(fù)荷預(yù)測(cè)結(jié)果

具體預(yù)測(cè)結(jié)果的數(shù)據(jù)對(duì)比如表1所示。

表1 四種神經(jīng)網(wǎng)絡(luò)12:00

時(shí)刻預(yù)測(cè)結(jié)果

(%)

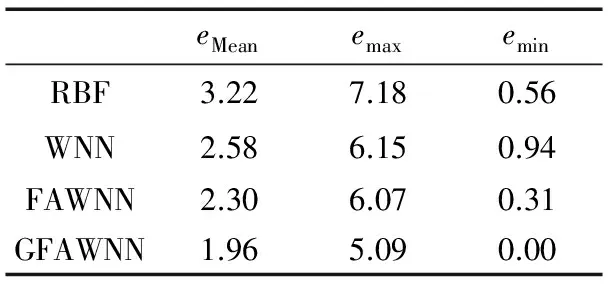
其中emax、emin、eMean分別表示測(cè)試樣本中最大的相對(duì)誤差、最小相對(duì)誤差和平均相對(duì)誤差。通過(guò)數(shù)據(jù)對(duì)比可知，改進(jìn)的GFAWNN網(wǎng)絡(luò)預(yù)測(cè)結(jié)果最佳，平均預(yù)測(cè)誤差和最大、最小預(yù)測(cè)誤差均最小。

4 結(jié)論

本文利用小波神經(jīng)網(wǎng)絡(luò)建立短期負(fù)荷預(yù)測(cè)模型，為了避免梯度下降法訓(xùn)練小波神經(jīng)網(wǎng)絡(luò)導(dǎo)致網(wǎng)絡(luò)陷入局部極小的問(wèn)題，本文用改進(jìn)的螢火蟲算法訓(xùn)練小波神經(jīng)網(wǎng)絡(luò)，確保螢火蟲個(gè)體始終保持活性并且螢火蟲個(gè)體之間具備足夠的吸引力以在全局范圍內(nèi)完成群體的迭代更新。迭代完成后的最優(yōu)個(gè)體即最優(yōu)解，是小波神經(jīng)網(wǎng)絡(luò)的最優(yōu)參數(shù)，根據(jù)最優(yōu)參數(shù)完成短期負(fù)荷預(yù)測(cè)。實(shí)驗(yàn)表明，在同等實(shí)驗(yàn)數(shù)據(jù)和實(shí)驗(yàn)條件下，優(yōu)化后的小波神經(jīng)網(wǎng)絡(luò)的預(yù)測(cè)精度較高。

[1] 牛東曉. 電力負(fù)荷預(yù)測(cè)技術(shù)及其應(yīng)用[M]. 北京：中國(guó)電力出版社, 2009.

[2] 余鳳, 徐曉鐘. 基于優(yōu)化小波BP神經(jīng)網(wǎng)絡(luò)的燃?xì)舛唐谪?fù)荷預(yù)測(cè)[J]. 計(jì)算機(jī)仿真, 2015, 32(1):372-376.

[3] 程聲烽, 程小華, 楊露. 基于改進(jìn)粒子群算法的小波神經(jīng)網(wǎng)絡(luò)在變壓器故障診斷中的應(yīng)用[J]. 電力系統(tǒng)保護(hù)與控制, 2014(19):37-42.

[4] 趙玉新. 新興元啟發(fā)式優(yōu)化方法[M].北京：科學(xué)出版社, 2013.

[5] Yang Xinshe. Firefly algorithm[M].Engineering,2010.

[6] 陸克中, 章哲慶, 孫俊. 保持個(gè)體活性的改進(jìn)FA算法[J]. 中國(guó)科學(xué)技術(shù)大學(xué)學(xué)報(bào), 2016(2):120-129.

[7] Liu Jiakun, Zhou Yongquan. Parallel glowworm optimization algorithm with master-slave structure[J]. Computer Engineering and Applications, 2012, 48(14):33-37.

[8] 賀蓉, 曾剛, 姚建剛,等. 天氣敏感型神經(jīng)網(wǎng)絡(luò)在地區(qū)電網(wǎng)短期負(fù)荷預(yù)測(cè)中的應(yīng)用[J]. 電力系統(tǒng)自動(dòng)化, 2001, 25(17):32-35.

Short-term load forecasting method of optimized wavelet neural network based on modified firefly algorithm

Liu Dan, Zhang Tengfei

(College of Automation, Nanjing University of Posts and Telecommunications, Nanjing 210023, China)

The traditional wavelet neural network is trained by the gradient descent algorithm, and the algorithm can easily lead to premature convergence and trap in local minimum, which affect the training accuracy of the network. In this paper, the firefly algorithm is used to train the wavelet neural network to search the optimal parameters of the network in the global. In order to improve the firefly algorithm’s ability of parameter optimization, the value ofγis adjusted adaptively in the training process. At the same time, Gauss variation is used to improve the activity of firefly individuals in order to ensure the convergence speed and avoid falling into local minimum. The optimized wavelet neural network is applied to short-term load forecasting, and the simulation results show that the improved prediction model has strong nonlinear fitting ability and high precision.

wavelet neural network; firefly algorithm; load forecasting; global optimization

國(guó)家自然科學(xué)基金項(xiàng)目(61105082)；江蘇省“青藍(lán)工程”基金(QL2016)；南京郵電大學(xué)“1311人才計(jì)劃”基金(NY2013)；江蘇省普通高校研究生科研創(chuàng)新計(jì)劃項(xiàng)目(SJLX15_0387)

TP391

A

10.19358/j.issn.1674- 7720.2016.23.016

劉丹，張騰飛. 基于改進(jìn)螢火蟲算法的小波神經(jīng)網(wǎng)絡(luò)短期負(fù)荷預(yù)測(cè)方法[J].微型機(jī)與應(yīng)用，2016,35(23)：56-58.

2016-08-15)

劉丹(1992-)，女，碩士研究生，主要研究方向：電力系統(tǒng)負(fù)荷預(yù)測(cè)。

張騰飛(1980-)，男，博士，副教授，碩士生導(dǎo)師，主要研究方向：智能信息處理、微電網(wǎng)運(yùn)行與控制等。