基于Kautz模型的永磁同步電動機調速系統電流預測控制
高旭東,許鳴珠,欒東雪
(石家莊鐵道大學,石家莊 050043)
?
基于Kautz模型的永磁同步電動機調速系統電流預測控制
高旭東,許鳴珠,欒東雪
(石家莊鐵道大學,石家莊 050043)
提出了一種基于Kautz模型的自適應增量式模型預測控制算法,并將該算法應用到基于DSP TMS280F2812的永磁同步電動機數字控制平臺上,實現了對永磁同步電動機電流的數字控制。根據數字控制平臺的局限性,作者對該算法進行了優化。大量實驗證明,提出的模型預測控制算法可以使永磁同步電動機電流控制系統具有較快的響應速度,較為平穩的運行狀態,較強的魯棒性,在電機控制領域具有較高的工程應用價值。
Kautz模型;模型預測控制;永磁同步電動機;電流控制;算法優化
0 引 言
永磁同步電動機(以下簡稱PMSM)的電流控制方法一般是采用控制器對電機的交、直軸電流分別進行控制,簡化了控制過程,提高了控制精度[1]。PMSM電流控制系統要求在滿足動態和靜態控制性能的同時,還要抑制非線性、參數時變等因素對系統的影響[2]。傳統的電流控制系統通常采用PID/PI控制,該方法原理上是一種線性調節器,靠目標與實際行為之間的誤差來決定控制策略,具有控制原理簡單、實現方便、控制參數彼此獨立、參數容易整定等優點[3-4]。但PID/PI控制器在應用中普遍存在噪聲和超調,很難同時保證響應的穩定性和快速性,在高性能控制場合存在一定的局限性。
模型預測控制(Model Predictive Control, MPC)是在20世紀70年代提出的,最初被用于復雜的工業控制領域。它是一種基于模型的控制算法,但是只對模型的功能有要求,對模型的形式沒有太多限制[5-6],利用具有預測功能的模型和當前系統狀態預測系統的未來狀態,在每個控制周期內利用最優控制方法根據系統的參數來對系統控制量輸入進行計算與優化,從而實現系統的快速、穩定控制[7]。文獻[8-9]介紹了基于Laguerre模型的預測控制算法,該系統對時延和模型的結構變化適應性較好,但是Laguerre模型是單極點網絡,能夠高效的逼近過阻尼系統,對于欠阻尼系統或特性變化較大的系統逼近效果較差[10-12]。而具有兩個極點的Kautz函數能夠有效地逼近控制系統模型[13],克服了Laguerre函數濾波網絡的局限性。本文利用截斷的Kautz函數模型[14]作為預測控制的函數模型,使用最優控制率對控制量進行優化,利用最小二乘法在線辨識模型參數,并根據硬件控制平臺芯片的特性以及控制效果的要求改進了預測控制算法,將位置式控制改為了增量式[15-16],降低系統運算量的同時也減小了系統誤差。通過大量實驗證明,基于Kautz模型的預測控制可以有效地解決了PID/PI控制器的局限性,實現對PMSM調速系統電流環的數字化控制。
1 Kautz函數模型
Kautz函數是平方可積函數空間上的一組正交基,濾波網絡擁有兩個極點,可以利用它來逼近欠阻尼系統或特性變化較大的情況,這種特性理論上完全適用于永磁同步電動機系統模型。文獻[10,17-18]詳細介紹了Kautz函數的定義以及網絡極點的取值以及截斷階次。將Kautz模型離散化以后可以表示為如下狀態方程的形式:
X(k+1)=A1X(k)+A2X(k-1)+BU(k)
y(k+1)=CX(k+1)
(1)
式中:U(k)=[u(k-1)u(k)]T;A1,A2,B是如下矩陣,其中的具體參數定義可參照文獻[11-12]。
由狀態空間方程可知方程狀態向量X(k+1)可以通過模型和系統輸入U(k)計算得到,則模型輸出y(k+1)可以由系數向量C和狀態向量X(k+1)獲得。向量C可以應用帶有遺忘因子的最小二乘辨識算法在線獲得。
(2)
式中:0<λ<1為遺忘因子。
2 基于Kautz模型的模型預測控制
基于Kautz函數逼近模型的模型預測控制算法主要分為預測模型、反饋矯正、滾動優化及參數辨識三部分,其控制結構如圖1所示。預測模型根據控制量狀態對系統輸出進行預測,并根據系統的反饋值和設定值進行滾動優化和參數辨識,實現了受控對象的最優控制。
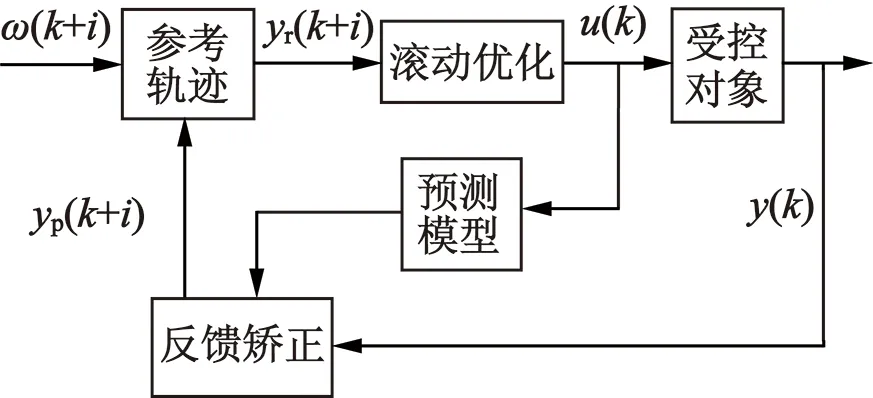
圖1 基于Kautz模型的模型預測控制結構框圖
考慮到本實驗平臺選用的DSP控制器處理數據的速度和能力,本著盡量減少運算量提高運算速度和控制精度的原則,將式(1)的狀態空間方程改為了增量型控制,將控制增量加入到預測模型中。則基于Kautz模型的增量型預測控制算法模型:
ΔX(k+1)=A1ΔX(k)+A2ΔX(k-1)+BΔU(k)
ym(k+1)=ym(k)+CΔX(k+1)
(3)
利用線性反饋預測理論[12],由式(3)可得未來k+i時刻的系統模型輸出:
ym(k+i)=ym(k)+CQaiΔX(k)+CQbiΔX(k-1)+
(4)
式中:參數Qai和Qbi表示下面的形式:
Qa1=A1;
Qa2=A1Qa1+A2;
Qa3=A1Qa2+A2Qa1;
…;
Qai=A1Qa(i-1)+A2Qa(i-2);
Qb1=A2;
Qb2=A1Qb1;
Qb3=A1Qb2+A2Qb1;
…;
Qbi=A1Qb(i-1)+A2Qb(i-2)
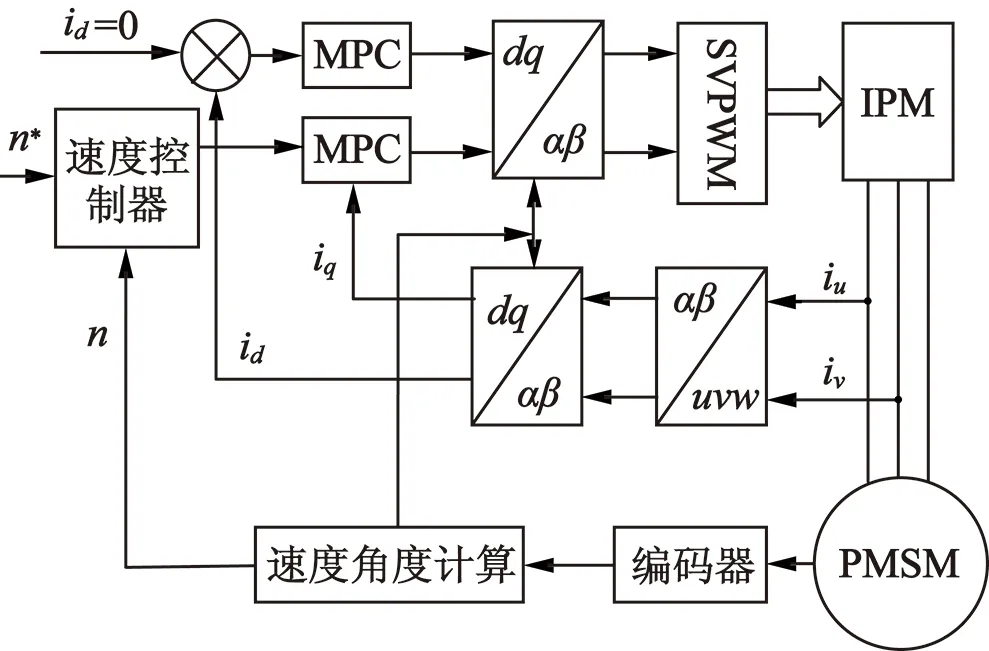
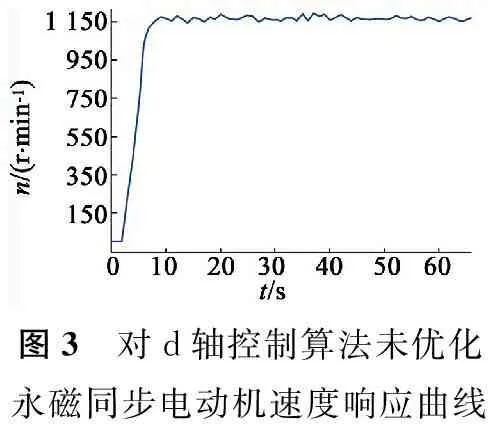
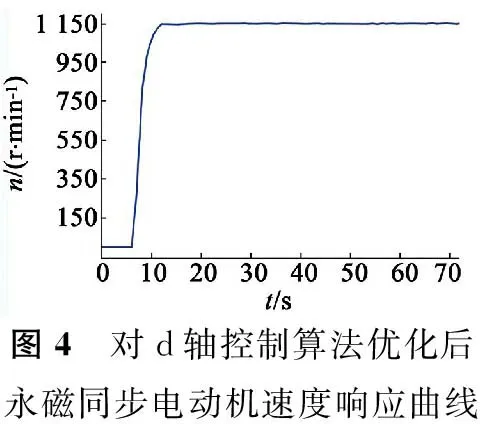
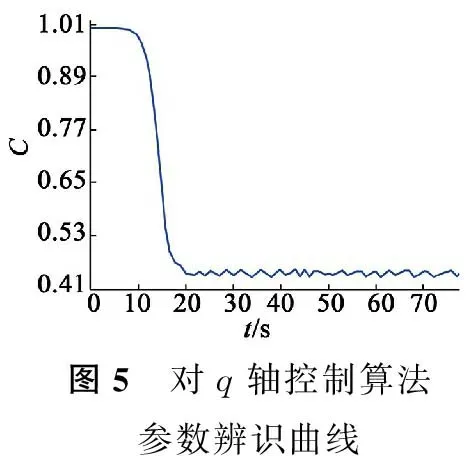
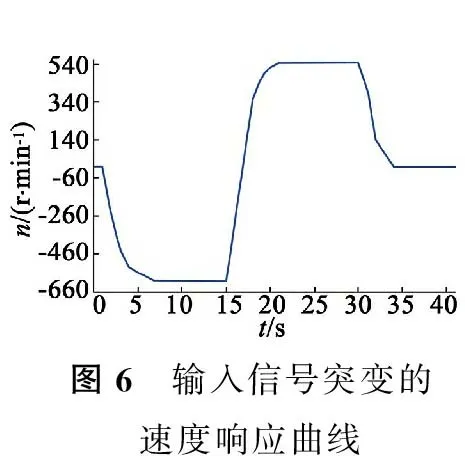
參數QjCi的取值規律如下:如果j=i,則QjCi=B2;如果j=i-1,則QjCi=A1QjC(i-1)+B1;如果j 將系統的預測控制增量方程寫為矩陣形式: GcΔu(k-1)+GU (5) 為了消除模型誤差以及實際過程中存在的干擾導致的輸出預測誤差,提高預測精度,本文采用反饋矯正來修正系統未來i時刻的預估值[9],即有: yp(k)=ym(k)+h[y(k)-ym(k)] (6) 式中:y(k)為k時刻系統的輸出;ym(k)為k時刻模型輸出;h為反饋增益值。 系統的參考軌跡取值為: yr(k+i)=αω(k)+(1-α)yp (7) 式中:ω(k)為系統設定值;α為柔化因子。 由二次型性能指標確定系統最優控制率: (8) 式中:Q,R分別為加系數權矩陣和誤差權系數矩陣,Q=diag(q1,…,qp),R=diag(r1,…,rm)。 (9) 式(9)中(GTQG+R)-1為一i×i維矩陣,可以一次計算出從k到k+i-1時刻的i個控制量,但在實際執行時,由于模型誤差、系統因自身特性以及外界因素的干擾等因素的影響,若按式(9)計算經過i步控制后可能會偏離參考軌跡較多[19]。同時該最優控制量的求解運算較為復雜,控制器硬件的計算能力也有限。為了能夠及時糾正誤差,減小控制器的運算負擔,對該最優控制算法進行改進。在應用中避免多維向量同時控制,盡量使用單輸入單輸出系統[16],即按式(9)算得控制量后,實際只執行當前一步,得出下一時刻控制增量Δu(k)。因此由式(9)得: Δu(k)=(1,0,…,0) (10) 從而得到k時刻系統實際控制量u(k)=u(k-1)+Δu(k),然后在下一周期繼續按式(10)遞推因此該方法被稱為“滾動優化”[7]。 在模型參數確定后,狀態向量X(k)可以由經過最優控制優化后的控制量輸入u(k)計算得到,因此模型輸出ym(k)與Kautz系數向量C有以下線性關系: ym(k)=CX(k) (11) 系數向量C可以通過帶遺忘因子的最小二乘法在線辨識獲得。 為了驗證本文所提預測控制算法對永磁同步電動機電流環控制的有效性,編寫相應程序將上述方法在永磁同步電動機控制系統上進行實驗。建立了以TI公司研發的TMS320F2812定點計算運動控制芯片為核心的永磁同步電動機數字伺服控制系統[20],其時鐘頻率為150 MHz,系統的控制周期為50 μs。驅動系統是由IGBT搭建的橋型電路,控制系統產生的SVPWM信號經過線性驅動后輸出給驅動系統,再由驅動系統將信號輸送給永磁同步電動機。采用的永磁同步電動機參數如下:200 W,36 V輸入,額定電流7.5 A,輸出轉矩0.637 N·m,磁極對數為4,轉子轉動慣量J=0.189×104 kg·m2線電感0.9 mH,線電阻0.33 Ω。永磁同步電動機采用的控制驅動方式為電壓空間矢量控制,控制器軟件設計采用的是C語言,所用的開發環境為CCS5.5,同時該開發環境可實時監測當前系統內各個變量的變化曲線,其程序結構控制方式如圖2所示。 圖2 永磁同步電動機程序結構控制方式 從控制意義上說,預測控制是一種實時的優化算法,它可以做到減小開關損耗、降低開關頻率、減小諧波損耗等優化目標[21]。對于目前的工業控制器來說,由于預測控制模型的數據變化動態范圍大,在線辨識運算要求的實時性較高,運算精度和速度都不能達到理想狀態。因此需要對模型預測的數據和結構進行優化。 4.1 控制算法的數據參數優化 本文使用的控制器為TI公司生產的定點運算控制器,由上文可知基于Kautz模型的預測控制的系數矩陣和控制量輸出均為浮點型數據,需將控制系統中的參數轉換為IQ整數格式進行運算。在實驗過程中監測的數據顯示,預測模型在進行計算尤其是進行參數辨識時數據動態范圍變化非常大,導致IQ格式數據精度不足或數據溢出。將所有數據改為浮點型運算,雖然導致運算周期變大,但運算精度能夠得到保證。 為了減輕DSP的運算負擔還將系統內的一些無需在線優化的參數做了離線計算,直接寫進程序中。在最優控制率計算中,計算結果只取所求矩陣的第一個元素,所以先在線下推導出求解第一個元素所需參數及其方程式,然后將該式直接寫入程序中,將大規模的矩陣運算轉變為多項式計算提高了程序運行的效率。 在實驗初期考慮到DSP數據的存儲量和運算能力,為了滿足系統高速實時控制的要求,提前計算出控制系統模型系數A1,A2,B,C,程序中直接使用固定常數。同時對控制系統進行3步預測控制,通過多步預測結果來彌補因系統模型系數降階固化產生的誤差。經過實驗,該優化方法大大提高了運算速度,在控制精度上也能夠滿足要求。 4.2 控制算法的結構優化 預測控制模型在初始啟動時,由于模型沒有經過辨識,誤差較大,造成輸出的控制量出現超調,導致永磁同步電動機出現運行卡頓、堵轉甚至過載的狀態,容易產生事故。因此需要對目前控制算法的控制方式進行優化。 ud(k)=Δud(k) (12) 由于d軸的數量級也會影響到控制量的在線優化,導致辨識誤差巨大。考慮到Kautz函數模型也較為龐大,在DSP中計算會影響到控制系統的實時性,所以將對d軸的模型預測控制系統參數改為了定值計算。即對d軸的預測控制系數C不進行在線辨識,而是通過實驗監測確定d軸C的一個取值范圍,直接將C設置為該范圍內的某個定值。而對于q軸的控制則按照前文所述算法模型進行預測控制,不做結構上的改變。 經過實驗驗證將算法優化后既減輕了DSP的運算負擔,又提高了整套系統的運算速度,d軸電流的控制精度也未受到影響。 本文利用基于Kautz模型的增量式模型預測控制算法對用于控制永磁同步電動機的電流,實現電機的快速啟動平穩運行。首先設定Kautz函數模型ξ=0.66+0.48i,設定q軸預測控制參數反饋增益h=0.9,柔化因子α=0.8,遺忘因子λ=0.99,系統參數C初值為1;d軸預測控制參數反饋增益h=0.9,柔化因子α=0.8,系統參數C定值為0.3。 為了驗證本文所提基于Kautz函數模型的預測控制對電機電流的控制效果,首先對比d軸在使用在線辨識和優化后使用固定值計算的控制效果,在給定系統一個1 150 r/min的階躍輸入信號后,圖3和圖4分別是對d軸控制算法優化前和優化后的輸出響應曲線。兩圖對比可知,當d軸不做優化,對系統參數做實時辨識的時候由于辨識誤差較大,DSP因在線辨識實時性變差最終導致電機運行不穩定,速度波動較大。當對d軸作了優化后,減小了DSP的運算量以及運算誤差,電機響應迅速平穩。對于q軸的控制,其系統參數需要進行在線辨識,為了觀察在線辨識的效果,作者在對d軸優化后,輸入階躍信號的同時對q軸模型預測控制系統的參數C變化進行了監控,如圖5所示,可觀察到系統參數辨識響應迅速,且在電機穩態運行時參數波動范圍小,呈現一定的周期性變化。 為了驗證永磁同步電動機面臨速度突變時系統的響應狀態,在靜止狀態給系統輸入一個反向600 r/min階躍信號,等待電機運行穩定后,再給系統一個正向600 r/min的輸入信號,最后等待電機運行平穩后再讓電機停止運行。系統轉速響應曲線如圖6所示。從圖中可以看出,模型預測控制的速度響應柔和、穩定、無超調量,并且響應時間也在系統響應允許的范圍內。在穩態運行時,系統速度穩定,抖動很小。 圖3 對d軸控制算法未優化永磁同步電動機速度響應曲線 圖4 對d軸控制算法優化后永磁同步電動機速度響應曲線 圖5 對q軸控制算法參數辨識曲線圖 圖6 輸入信號突變的速度響應曲線 本文將所提的基于Kautz模型的增量式模型預測控制算法應用于永磁同步電動機數字調速系統的電流控制中。針對實驗系統硬件特性對模型算法進行了優化,實驗證明DSP系統完全可以在規定的時間內將控制量計算輸出,實現了永磁同步電動機的高性能控制。本文所提控制算法不需要知道控制系統的具體模型,通過帶有遺忘因子的最小二乘法在線辨識控制系統參數,提高了該控制算法的適用范圍。基于Kautz模型的預測控制計算量較大,應用起來較為復雜,對硬件系統要求高,所以該算法可應用于一些系統性能要求高、投資大的場合,具有較高的實際應用價值。 [1] 牛里,楊明,劉可述,等.永磁同步電機電流預測控制算法[J].中國電機工程學報,2012,32(6):131-137. [2] 袁登科,陶生桂.交流永磁電機變頻調速系統[M].北京:機械工業出版社,2011. [3] 趙景波.MATLAB控制系統仿真與設計[M].北京:機械工業出版社,2010. [4] 孟芳芳,邵雪卷.基于DSP感應電機預測函數控制數字實現[J].微電機,2014,47(11):38-41. [5] 丁寶蒼.預測控制的理論與方法[M].北京:機械工業出版社,2008. [6] 席裕庚.預測控制[M].北京:國防工業出版社,1993. [7] 鄭澤東,陳寧寧,李永東.基于模型預測控制的異步電機弱磁控制新方法[J].電工技術學報,2014,29(3):33-40. [8] 李嗣福,劉勇.一種基于Laguerre函數模型的預測控制算法[J].中國科技大學學報,1999,29(3):281-288. [9] 吳麗娟,張寧,謝元旦.基于Laguerre級數模型的自適應動態矩陣控制[J].控制與決策,1997,12(1):37-42. [10]WAHLBERGB.SystemidentificationusingKautzmodels[J].IEEETransactionsonAutomaticControl,1994,39(6):1276-1282. [11] 許鳴珠,劉賀平,李曉理,等.基于KAUTZ模型的預測控制仿真研究[J].系統仿真學報,2007,19(15):3481-3484. [12] 許鳴珠,劉賀平,李曉理,等.基于KAUTZ模型的預測函數控制及其穩定條件[J].北京科技大學學報,2007,29(11):1171-1176. [13]TANGUYN,MORVANR,VILBEP,etal.PertinentchoiceofparametersfordiscreteKautzapproximation[J].IEEETransactionsonAutomaticControl,2002,47(5):783-787. [14]DENBRINKERAC,BENDERSFPA,OLIVEIRAESTAM.OptimalityconditionsfortruncatedKautzseries[J].IEEETransactionsonCircuitsandSystems,1996,43(2):117-122. [15] 姚偉,孫海順,文勁宇,等.基于Laguerre模型的過熱汽溫自適應預測PI控制系統[J].中國電機工程學報,2012,32(5):119-125. [16] 鄭澤東,王奎,李永東,等.采用模型預測控制的交流電機電流控制器[J].電工技術學報,2013,28(11):118-123. [17]MBAREKA,MESSAOUDH,FAVIRG.RoubustpredictivecontrolusingKautzmodel[C]//Proceedingsofthe2003 10thIEEEInternationalConferenceonElectronics,Circuits,andSystems,2003:184-187. [18]MORVANR,TANGUYN,VILBEP.PertinentparametersforKautzapproximation[J].ElectronicsLetters(S0013-5194),2000,36(8):769-771. [19] 舒迪前.預測控制系統及其應用[M].北京:機械工業出版社,1996. [20] 紀科輝,沈建新.采用擾動轉矩觀測器的低速電機伺服系統[J].中國電機工程學報,2012,32(15):100-106. [21] 李永東.交流電機數字控制系統[M].2版.北京:機械工業出版社,2014. Current Predictive Control of PMSM Speed Control System Based on Kautz Model GAOXu-dong,XUMing-zhu,LUANDong-xue (Shijiazhuang Tiedao University, Shijiazhuang 050043,China) An adaptive incremental model predictive control algorithm based on Kautz model was proposed.And the algorithm was applied to the digital control platform of permanent magnet synchronous motor based on TMS280F2812 DSP, and the digital control of permanent magnet synchronous motor current was realized.According to the limitation of the digital control platform, the optimization to the algorithm was carried on.After a large number of experimental studies show that the model prediction control algorithm proposed in this paper can make the permanent magnet synchronous motor current control system has fast response speed, stable running, strong robustness, and has higher engineering application value. Kautz model; model predictive control (MPC); PMSM; current control; algorithm optimization 2015-12-07 國家自然科學基金面上項目(11372198);河北省教育廳科學技術重點項目(Z9900451) TM351 A 1004-7018(2016)09-0078-05 高旭東(1990-),男,碩士研究生,研究方向為永磁同步電機調速系統設計、機電系統控制及自動化。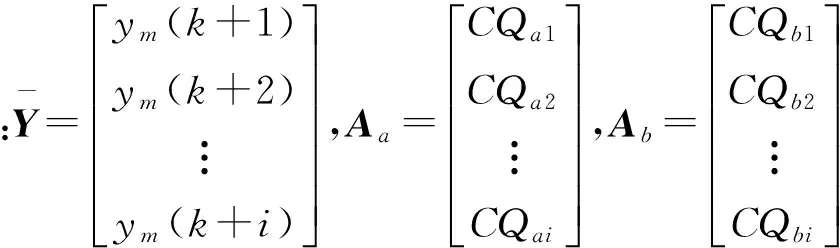

3 實驗平臺描述
4 基于實驗平臺的算法優化
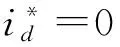
5 實驗分析對比
6 結 語

