動態光散射顆粒分布軟測量

田慧欣，彭 曉，朱新軍，孟 博

(1.天津工業大學 電氣工程與自動化學院，天津 300387；2.天津工業大學 電工電能新技術天津重點實驗室，天津 300387)

?

動態光散射顆粒分布軟測量

田慧欣*，彭 曉，朱新軍，孟 博

(1.天津工業大學 電氣工程與自動化學院，天津 300387；2.天津工業大學 電工電能新技術天津重點實驗室，天津 300387)

考慮傳統動態光散射顆粒粒度分布測量用的反演算法復雜、精度不夠、抗噪能力差， 本文基于大數據思想，提出了一種動態光散射顆粒分布軟測量方法。該方法通過調節顆粒粒度分布形狀參數獲得大量自相關函數及其對應顆粒分布的數據；使用這些數據對子學習機進行訓練。最后，針對訓練數據維數較高的特點對傳統Bagging算法進行改進，并利用改進的Bagging集成算法集成子學習機以提高軟測量模型的精度及泛化能力。通過模擬單峰數據和對300 nm標準粒徑進行軟測量開展了驗證實驗。結果表明，該方法能夠較好地測量出不同動態光散射顆粒分布的峰值及分布寬度，模擬單峰數據測量峰值精度可達1 nm，300 nm和503 nm，標準粒徑測量精度分別可達3 nm和4 nm，優于一般的反演算法。該軟測量方法為動態光散射顆粒分布測量開辟了新的途徑。

動態光散射；顆粒分布測量；軟測量；Bagging算法

1 引 言

亞微米顆粒以及納米顆粒在電、磁、光、熱、聲等各個方面都有其特殊性。隨著新材料工業生產的迅猛發展，納米顆粒由于具有表面效應和宏觀量子隧道等特點，其應用也日益增多[1-2]。此外，在動態的乳膠聚合過程中以及對DNA、細胞等特性研究中，納米顆粒的自身粒徑也會給實驗結果帶來較大影響[3]。通常用來表征納米顆粒性能的參數是粒度的大小及其粒度分布。對同質納米而言，不同的顆粒大小或是不同的顆粒分布都將影響到其特異性能[4]。因此，顆粒粒度及其分布的精準測量對于實際應用具有重要意義。

動態光散射技術是測量亞微米顆粒及納米顆粒粒度分布的主要測量技術。該技術采用密封測量的方式，不會破壞和干擾樣品的原有狀態，具有快速、便捷、可靠以及非侵入性等特點，在生物、化學和高分子材料等領域應用廣泛[5]。動態光散射技術一般通過散射光相關函數反演求解的方法來獲取顆粒粒度分布。在反演求解第一類Fredholm積分方程過程中，相關函數的測量需在無噪聲的環境下進行，在數據的運算中也應盡量避免舍入誤差的存在。但求解此類積分方程屬于一個不適定病態數學問題，數據中一個微小的擾動都極有可能產生巨大誤差，從而無法得到準確的顆粒粒度分布，使測量失去意義。因此，找尋最接近于真實粒度分布的反演算法是動態光散射技術中的重難點問題。針對上述問題，近些年來學者們提出了多種反演算法，其中被廣泛使用的有累積法、指數法和非負約束最小二乘法，但這些方法對寬峰數據的分布測量效果較差，而CONTIN以及貝葉斯算法[6-9]等對不同顆粒的測量效果不同，算法穩定性有待提高。為了提高反演算法的精度，王靜雅等結合Tikhonov正則化與瀑布型多重網格技術將原反演問題分解到多尺度網格空間，以降低求解難度[10]，曹麗霞等改進Chahine算法以提高反演結果的平滑性及穩定性[11]。另一方面，一些研究者通過分析光學相關譜、散射光譜估計等理論，并與光學系統、光電探測器等硬件測量技術相結合，完成對動態光散射顆粒分布的測量[12-13]。大多數反演算法都需要大量先驗知識來確定相關的參數，因此人工干預較多，存在抗噪能力差，測量精度低等不足。使用硬件設備雖然測量精度高，但儀器價格昂貴。針對已有測量方法的不足，本文將軟測量概念引入動態光散射顆粒分布測量中，提出一種基于改進Bagging的人工智能集成方法，從大量顆粒分布與相關函數的數據中獲取信息，建立顆粒分布軟測量模型，巧妙地回避了求解Fredholm積分方程這一難題，有效地克服了傳統方法需要大量先驗知識、抗噪能力差的不足，為動態光散射技術測量顆粒分布提供了新的可靠途徑。

2 改進Bagging的顆粒分布軟測量

2.1 動態光散射顆粒分布軟測量模型的建立

對隨機的散射光信號進行相關運算并作歸一化處理，可以得到歸一化的散射光強自相關函數g(2)(τ)，它與歸一化的電場自相關函數g(1)(τ)的關系為：

(1)

式中：τ是延遲時間，A是實驗基線，β是相干因子。

對于多分散顆粒系，歸一化的電場自相關函數的分布積分為：

(2)

在求解方程(2)得到G(Γ)后，通過衰減線寬—平移擴散系數—顆粒粒徑換算后，可求得顆粒粒徑的分布G(d)。式(2)為第一類Fredholm積分方程，而且在g(1)(τ)中不可避免地存在著噪聲，在此情況下求解顆粒粒徑分布屬于病態問題，解通常會發生嚴重偏離，甚至無法求解[14-16]。而如果已知G(Γ)，則可以很容易地求得g(1)(τ)，因此可以考慮利用這一特性獲得分布函數及自相關函數的大量數據，再使用人工智能方法對這些數據進行學習，并建立顆粒粒徑分布函數的軟測量模型，從而實現對顆粒分布的測量，如圖1所示。

圖1 基于Bagging的顆粒分布軟測量結構圖

Fig.1 Structure diagram of soft measurement of particle distribution based on Bagging

2.2 基于改進Bagging的顆粒分布軟測量集成算法

作為一種新的機器學習方式，集成學習的測量精度較傳統單一學習算法高。其基本思想是將多個精度較低的弱學習機集成，得到一個較強的學習機[17]。Bagging集成算法首先通過bootstrap，即有放回式的抽樣方法，得到相應數量的子訓練集，然后使用子訓練集對弱學習機進行訓練，最后將訓練弱學習機得到的結果進行集成得到強學習機，并輸出最終結果。在訓練過程中，各子數據集相互獨立，測量子函數并行生成，因此，集成后的最終模型精度以及泛化性能均得到了很大的提高[18]。

改進后用于顆粒分布軟測量的Bagging集成方法結構圖如圖2所示。

圖2 基于Bagging的集成軟測量模型結構圖

Fig.2 Structure diagram of integrated soft measurement model based on Bagging

輸入：

(1)數據集Data樣本數量為m：

其中y=y1，y2，…，yR。

(2)確定子學習機算法。

(3)確定子學習機個數T以及子訓練集的大小L。

(4)設定閾值參數φ=(φ1，φ2，…，φR)(φ>0)。

循環：t=1，2，3，…，T

(1)采用bootstrap抽樣方法抽取L個數據組成的訓練子集St。

(3)

(4)

(5)計算權重因子：

(5)

輸出：

(6)

較傳統的反演推導算法而言，使用軟測量方法獲取動態光散射顆粒分布的精度較高，操作簡單，只需在實驗訓練過程中調整閾值參數以獲取準確的模型，無需繁復的先驗背景知識以及復雜的數學推導過程，為研究動態光散射顆粒分布提供了另一種可能。

3 實 驗

3.1 測試數據測量實驗

在用已知G(Γ)反推求解g(1)(τ)的過程中，通過改變100～800 nm單峰顆粒Johnson’sSB參數u與σ，獲取實驗所需175種顆粒粒度分布數據用于訓練模型，其中u∈(0.8，3)，σ∈(1.8，6.8)，數據噪聲水平為105。訓練數據的輸入為200維，輸出為70維。測試數據分為5組，其參數如表1所示。

表1 測試數據對應參數表

均方根誤差RMSE的計算公式如式(7)所示：

(7)

實驗采用三層的BP(Back Propagation)神經網絡作為子學習機，子學習機個數為40，子訓練集大小為100。建立好軟測量模型后，使用5組測試數據進行實驗仿真。1、2、3組數據加入的噪聲水平相同，峰值不同；3、4、5組數據峰值相同加入的噪聲水平不同。噪聲水平的值越大說明該數據噪聲越小。5組數據的峰值、寬度分布及均方根誤差如表2所示，測量分布圖如圖3、圖4所示。

(a)第1組參數測量結果(u=1.5，σ=6.8)

(b)第2組參數測量結果(u=3，σ=2.6)

(c)第3組參數測量結果(u=1.5，σ=2.6)

(a)第3組參數測量結果(noise factor=1×105)

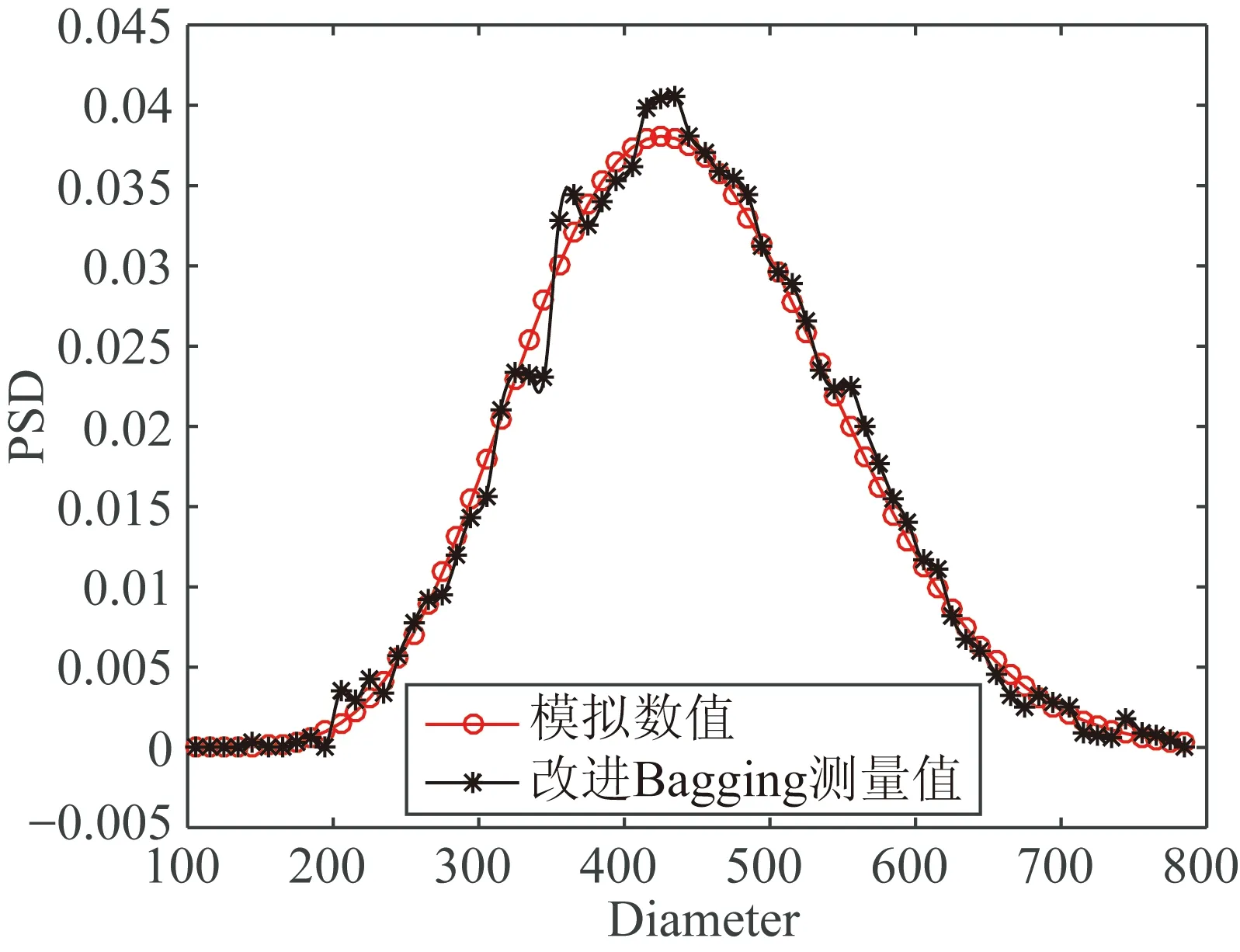
(b)第4組參數測量結果(noise factor=1×1010)

(c)第5組參數測量結果(noise factor=1×1015)

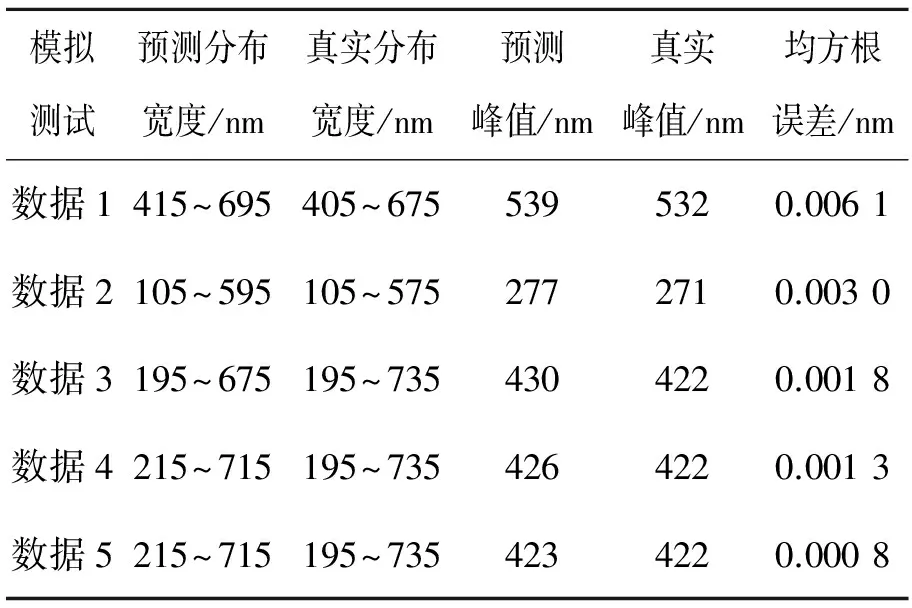
模擬測試預測分布寬度/nm真實分布寬度/nm預測峰值/nm真實峰值/nm均方根誤差/nm數據1415～695405～6755395320．0061數據2105～595105～5752772710．0030數據3195～675195～7354304220．0018數據4215～715195～7354264220．0013數據5215～715195～7354234220．0008

實驗結果表明，軟測量方法獲得的顆粒分布精度較高且抗噪性能良好。針對不同的動態光散射顆粒分布，測量總體效果較好，分布寬度的預測值與真實值大致相同，峰值誤差較小，精度可達到8 nm。在加入噪聲后，軟測量建模算法的誤差增大，但隨著噪聲的增加，誤差增長幅度較小，有一定的抗噪性能。

3.2 真實數據測量實驗

300 nm與503 nm標準顆粒采用MilliPore Milli-Q/ Milli-Rho系統去離子蒸餾水稀釋，稀釋后的300 nm(3 300 A)顆粒濃度為3.0×10-4wt%，503 nm(3 500 A)顆粒濃度為2.0×10-4wt%。樣品池溫度控制在25 ℃，Ar+激光器的激光功率為50 mW，將通道BI-2030AT 72相關器測量的粒徑作為標準粒徑用于數據的對比。對于300 nm標準粒徑，相關器測量值為324 nm±2 nm，對于503 nm標準粒徑，相關器測量值520 nm±4 nm。

實驗分別使用改進Bagging的軟測量方法與基于二階光強相關函數的改進反演算法[2]對300 nm 與503 nm標準顆粒數據進行分布測量，其中反演算法采用約束Tikhonov正則化，參數選取為固定值0.005。圖5為兩種算法得到的300 nm顆粒與503 nm顆粒分布圖。

(a) 300 nm顆粒反演結果與軟測量結果對比圖

(b) 503 nm顆粒反演結果與軟測量結果對比圖

圖5表明，軟測量方法得到的300 nm標準顆粒峰值為303 nm，精度為3 nm；503 nm標準顆粒峰值為507 nm，精度為4 nm。而反演算法得到的300 nm標準顆粒峰值為295 nm，精度為5 nm；503 nm標準顆粒峰值為513 nm，精度為10 nm。較真實的標準顆粒而言，軟測量方法精度較高，而且軟測量得到的分布寬度比反演算法得到的分布寬度窄，較為穩定。

4 結 論

本文根據動態散射光顆粒的特點，與軟測量技術相結合，提出了改進Bagging的高維度軟測量方法。首先通過反求解的方法求解第一類Fredholm積分方程獲得大量不同的動態光散射顆粒分布數據。然后用所獲取的數據訓練子學習機。最后將子學習機集成為最終的軟測量模型并使用測試數據進行檢驗。實驗結果表明，對于模擬數據，該軟測量方法的峰值精度最高可達1 nm，對于真實數據精度最高可達3 nm，精度優于反演算法。本文所研究的軟測量技術為動態光散射顆粒分布的測量提供了新的可靠途徑。

[1] 王雅靜，鄭剛，申晉，等. 用于動態光散射顆粒測量的改進雙指數算法[J].中國激光，2009，36(s2)：173-177. WANG Y J， ZHENG G， SHEN J，etal.. Improving double exponential algorithm for particle sizing in dynamic light scattering [J].ChineseJournalofLasers， 2009，36(s2)：173-177.(in Chinese)

[2] ZHU X， SHEN J， WANG Y，etal.. The reconstruction of particle size distributions from dynamic light scattering data using particle swarm optimization techniques with different objective functions [J].Optics&LaserTechnology， 2011， 43(43)：1128-1137.

[3]SCHURTENBERGER P， SCHEFFOLD F， SHALKEVICH A，etal.. PCS particle sizing in turbid suspensions： scope and Limitations [J].ModelingAnalysis&SimulationofComputers&TelecommunicationSystems，mascots.ie， 2004， 21(1)：28-46.

[4] SHI W， SONG J， ZHU X，etal.. Design of weighing transmitter in corn yield measurement system [C]ProceedingsoftheFirstElectricInformationandControlEngineering，Wuhan，P.R.China：ICEICE， 2011：324-327.

[5] MORRISON I D， GRABOWSKI E F， HERB C A. Improved techniques for particle size determination by quasi-elastic light scattering [J].Langmuir， 2002， 1(4)：496-501.

[6] PROVENCHER S W. A constrained regularization method for inverting data represented by linear algebraic or integral equations [J].ComputerPhysicsCommunications， 1982， 27(3)：213-227.

[7] CLEMENTI L A， VEGA J R， GUGLIOTTA L M，etal.. A Bayesian inversion method for estimating the particle size distribution of latexes from multiangle dynamic light scattering measurements [J].Chemometrics&IntelligentLaboratorySystems， 2011， 107(1)：165-173.

[8] ZHU X， SHEN J， THOMAS J C. Analysis of noisy dynamic light scattering data using constrained regularization techniques [J].AppliedOptics， 2012， 51(31)：7537-7548.

[9] LIU X Y， SHEN J， THOMAS J C，etal.. Multiangle dynamic light scattering analysis using angular intensity weighting determined by iterative recursion [J].AppliedOptics， 2012， 51(7)：846-854.

[10] 王雅靜，申晉，鄭剛，等.Tikhonov正則化與多重網格技術相結合的動態光散射反演[J].光學 精密工程，2012，22(5)：963-971. WANG Y J， SHENG G， ZHEN G，etal.. Invertion of dynamic light scattering combining Tikhonov regularization with multi-grid technique [J].Opt.PrecisionEng.，2012，22(5)：963-971.(in Chinese)

[11] 曹麗霞，趙軍，孔明，等 基于改進的Chahine迭代算法的粒徑分布反演[J]. 紅外與激光工程，2015，44(9)：2837-2843. CAO L X， ZHAO J， KONG M，etal.. Inversion of particle size distribution based on improved Chahine algorithm [J].InfraredandLaserEngineering， 2015，44(9)：2837-2843.(in Chinese)

[12] 楊暉，鄭剛，張仁杰. 用動態光散射時間相干度法測量納米顆粒粒徑[J]. 光學 精密工程，2011，19(7)：1546-1551. YANG H， ZHENG G， ZHANG R J. Measurement of nanoparticle sizes by variance of temporal coherence of dynamic light scattering [J].Opt.PrecisionEng.， 2011，19(7)：1546-1551.(in Chinese)

[13] 楊暉，鄭剛，王雅靜. 用動態光散射現代譜估計法測量納米顆粒[J]. 光學 精密工程，2010，18(9)：1996-2001. YANG H， ZHENG G， WANG Y J. Measurement of nano-particles by dynamic light scattering based on spectral estimation [J].Opt.PrecisionEng.， 2010，18(9)：1996-2001.(in Chinese)

[14] GAO S， SHEN J， THOMAS J C，etal.. Effect of scattering angle error on particle size determination by multiangle dynamic light scattering [J].AppliedOptics， 2015， 54(10)：2824-2831.

[15] KIM J， AHN S， LEE H，etal.. Estimation of particle size distribution using photon autocorrelation function from dynamic light scattering considering unknown baseline[J].OpticsLetters， 2013， 38(11)：1757-1759.

[16] ClEMENTI L A， VEGA J R， GUGLIOTTA L M. Particle size distribution of multimodal polymer dispersions by multiangle dynamic light scattering. solution of the inverse problem on the basis of a genetic algorithm [J].Particle&ParticleSystemsCharacterization， 2012， 27(5-6)：146-157.

[17] TIAN H X， MAO Z Z， WANG A. A new incremental learning modeling method based on multiple models for temperature prediction of molten steel in LF[J].IsijInternational， 2009， 49(1)：58-63.

[18] TIAN H X， MAO Z Z， WANG Y. Hybrid modeling of molten steel temperature prediction in LF[J].IsijInternational， 2008， 48(1)：58-62.

田慧欣(1978-)，女，遼寧撫順人，副教授，2005年、2009年于東北大學分別獲得碩士、博士學位，主要從事人工智能軟測量及應用研究。E-mail： tianhuixin@tjpu.edu.cn

彭 曉(1992-)，女，湖北孝感人，碩士研究生，主要研究方向為人工智能軟測量方法及光干涉測量的研究。E-mail： 853050658@qq.com

(版權所有 未經許可 不得轉載)

Soft sensing of particle size distribution in dynamic light scattering measurement

TIAN Hui-xin*， PENG Xiao， ZHU Xin-jun， MENG Bo

(1. School of Electrical Engineering & Automatic，TianjinPolytechnicUniversity，Tianjin300387，China；2.KeyLaboratoryofAdvancedElectricalEngineeringandEnergyTechnologyinTianjin，TianjinPolytechnicUniversity，Tianjin300387，China)

As the traditional inversion algorithms for particle size distribution measurement by dynamic light scattering show complex computation， lower accuracy and poorer anti-noise capacity， this paper proposes a soft sensing method for particle size distribution based on improved Bagging algorithm by using idea big data. The data of autocorrelation function and particle sizing distribution were obtained by changing the parameters of particle distribution shape. Then the learning machines were trained by the data. Finally， the traditional Bagging algorithm was improved on the basis of the character of high dimensional data. The improved Bagging strategy was used to aggregate the machines for bettering the model accuracy and its generalization performance. A validation experiment was performed by simulating the single peak data and soft sensing for the standard particles with a diameter of 300 nm. Experiment results demonstrate that the proposed method predicts the peak position and the width of particle sizing distribution accurately， and the best accuracy of peak position measurement is 1 nm. Meanwhile， the accuracies for standard particles with diameters of 300 nm and 503 nm are 3 nm and 4 nm， respectively. The proposed method provides a new way for the particle size distribution measurement in dynamic light scattering.

dynamic light scattering； particle size distribution measurement； soft sensing； Bagging algorithm

2016-07-02；

2016-09-01.

國家自然科學基金資助項目(No.61403277；No.71602143)

1004-924X(2016)11-2814-07

TP301；TB92

A

10.3788/OPE.20162411.2814

*Correspondingauthor，E-mail：tianhuixin@tjpu.edu.cn