任意載彈模式俯仰系統重力矩算法研究

方 航,黃朝學,王敏毅

(中國船舶重工集團公司第710研究所,湖北宜昌 443003)

?

任意載彈模式俯仰系統重力矩算法研究

方 航,黃朝學,王敏毅

(中國船舶重工集團公司第710研究所,湖北宜昌 443003)

為實時解算某型火箭發射裝置俯仰系統重力矩,基于質點系等效質心原理推導出任意載彈模式下重力矩算法模型,采用Matlab編程實現算法并同Pro/E測量計算實際值對比分析。仿真結果表明,該算法滿足任意載彈模式下重力矩實時解算要求并達到較高精度,有效解決當前采用Pro/E軟件測量并計算重力矩方法工作量大且通用性差等缺點,極大的提高研究效率。

任意載彈模式;火箭發射裝置;重力矩;軟件算法

0 引言

俯仰系統重力矩大小與載彈模式參數相關,包括高低射角、剩余載彈量、彈種及彈位。當前重力矩主要由平衡機[1]平衡,為設計其結構[2-3]參數,需要獲取重力矩負載值作為設計目標,采用Pro/E軟件測量俯仰系統重心位置并計算重力矩負載值不僅工作量大且載彈模式改變時需要重新測量計算。

為實時自動解算重力矩負載,必須建立俯仰系統在任意載彈模式下的重力矩算法模型。同當前使用Pro/E軟件測量計算固定載彈模式下重力矩方法相比,本算法根據相關傳感器采樣獲取的參數實時解算俯仰系統在任意載彈模式下的重力矩負載,允許工程技術人員實時簡便獲取俯仰系統的重力矩大小值,極大的減少工作量。

1 重力矩模型算法原理

基于引言分析,假設高低角為θ、剩余載彈量為n、火箭彈種類為s、剩余載彈量分布位置編號為p,重力矩為MG,則必然存在以下函數關系:

MG=f(θ,n,s,p)

(1)

如圖1所示俯仰系統由多個質量體組成,包括發射架、火箭彈及附屬組部件,各質量體自身質心位置已知。假設系統中有N個質量體,質量均集中于質心處,第i個質量體在全局坐標系中的質心坐標為(xi,yi,zi),其質量為mi,該系統的等效質心記作(xe,ye,ze),根據文獻[4]可知系統等效質心滿足以下約束條件:

(2)

(3)

(4)

暫且忽略不計。

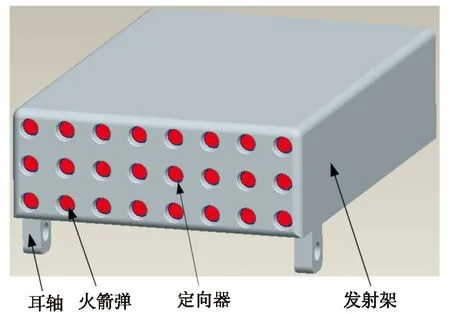
圖1 俯仰系統基本組成

2 重力矩模型函數建立

2.1 火箭彈等效質心向量模型

假設以發射架左下角端點建立全局坐標系O0(x0,y0,z0),第i根發射管內火箭彈尾部端面中心建立局部坐標系Oi(xi,yi,zi)并以平行于炮管z0方向為zi軸、平行于x0方向為xi軸、平行于y0方向為yi軸,詳見圖2、圖3所示。在局部坐標系Oi下火箭彈質心記作Gi(xGi,yGi,zGi),x0方向相鄰兩發射管中心間距為W,y0方向相鄰發射管中心間距為H,根據文獻[5]求O0坐標系下第i根發射管火箭彈質心向量滿足:

O0Gi=(x1+nW+xGi)i+

(y1-mH+yGi)j+(z1+zGi)k

(5)

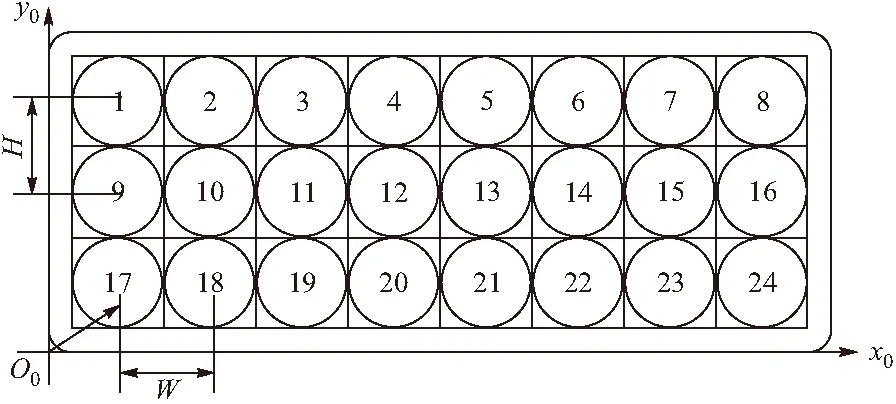
圖2 俯仰系統發射管位置編號及全局坐標系

圖3 火箭彈1質心及其局部坐標系

假設24根發射管位置視作3行8列矩陣,起始下標均記0,以此類推任意炮管位置編號i記作pi[m][n],建立位置編號pi和對應的數組元素行坐標m、列坐標n之間的函數關系,方便編程及軟件實時解算。經理論分析并歸納函數關系如下:

pi=8m+n+1

(6)

定義取整符號[A],表示對數據A舍去小數部分取整數部分,將取整符號用于本模型得:

(7)

(8)

推導出火箭彈全局質心計算公式為:

(9)

2.2 俯仰系統重心坐標計算

假設該火箭發射裝置配裝彈藥為A、B型彈，質量記作mA、mB,某次作戰剩余A、B型彈數量為NA、NB枚,第i枚A型彈位置編號為pAi、A型彈在O0坐標系下的質心等效坐標為(XGAi,YGAi,ZGAi),第j枚B型彈位置編號為pBj、B型彈在O0坐標系下的質心坐標為(XGBj,YGBj,ZGBj),A型彈局部質心坐標為(aA,bA,cA),B型彈局部質心坐標為(aB,bB,cB),發射架質量為mf、質心全局坐標為(Xf,Yf,Zf),俯仰系統等效重心坐標記作Oe(Xe,Ye,Ze),i、j為下標索引。依據文獻[5],發射裝置俯仰系統等效重心坐標計算公式推導如下:

(10)

(11)

(12)

(13)

(14)

(15)

(16)

ZGAi=z1+cA

(17)

ZGBj=z1+cB

(18)

式中0≤NA+NB≤N且為正整數。

2.3 俯仰系統重力矩模型函數

據文獻[4],為求解模型函數方便,以兩耳軸端面中心點連線中點為原點建立坐標系Or,以耳軸中心線為x軸,平行發射管軸向方向為z軸,垂直x軸、z軸的第三方向為y軸。

OrOe=OrO0+O0Oe

(19)

式中O0Oe為俯仰系統等效質心向量,假設OrO0=-d1i-d2j-d3k,綜合式(10)～式(19)可得:

OrOe=(Xe-d1)i+(Ye-d2)j+(Ze-d3)k

(20)

(21)

MG=(mf+NAmA+NBmB)·

(22)

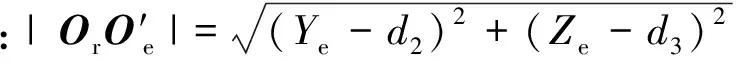
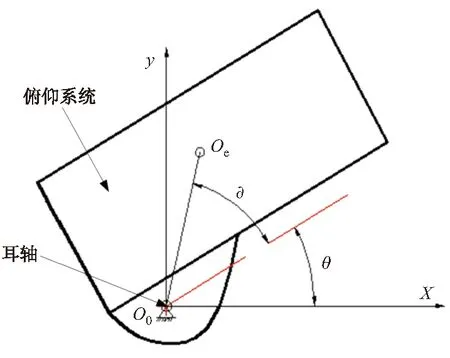
圖4 俯仰系統重力矩參數示意圖

3 算法實現及仿真計算

3.1 Matlab算法實現

根據重力矩算法編制用戶界面GUI如圖5所示,算法的Matlab實現代碼作為GUI中的控件回調函數。為確保輸入A和B兩種彈藥的位置編號出現重復,軟件特設計彈位免重報警功能,如果軟件檢測到手動輸入位置編號重復,則彈位免重報警燈亮(紅色),提示用戶查檢。確認參數無誤,單擊計算按鈕,則該載彈模式下重力矩大小值將顯示在結果欄。

3.2 算法仿真計算

為檢驗該算法正確性及實用性,使用Pro/E軟件測量俯仰系統在不同載彈模式下的重心位置,將計算的實際重力矩值同本算法計算的理論結果對比分析。由于俯仰系統載彈模式種類眾多,不可能驗證所有的工況,特任意選擇兩種工況作為評估該算法正確性的依據。

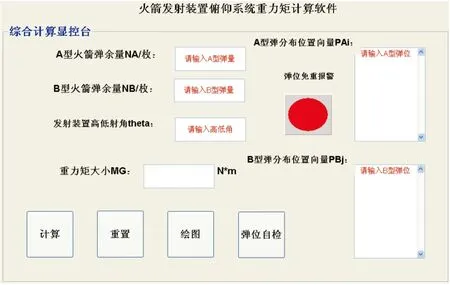
圖5 俯仰系統重力矩計算軟件GUI

工況1:假定發射管初始配裝A型彈24管,高低角θ=0°,每次發射一枚,發射順序為1,2,3,…,24,理論重力矩記作MGL、實際重力矩記作MGS,工況1的仿真結果如圖6～圖7所示。

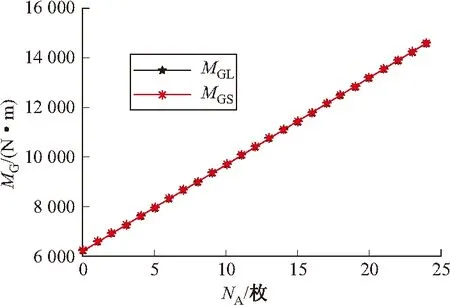
圖6 理論與實際重力矩結果對比

圖7 重力矩絕對誤差Ea與相對誤差Er

結果分析:曲線表明,實際重力矩結果與理論重力矩結果基本吻合(見圖6),最大絕對誤差Ea,max=0.144 4N·m、最大相對誤差Er,max=9.89×10-6<0.1%,工況1下該算法計算結果正確且精度較高,存在極小的誤差原因在于載彈模式參數獲取存在誤差,對理論結果有直接影響。

工況2:假設發射裝置初始配裝24枚彈藥,見表1。

因戰術需要發射裝置在θ=18°時發射B1、B2、B3共3枚B型彈;

θ=20°時發射B4、B5、B6、B7、 B8共5

枚B型彈;θ=22°時發射B9、B10、B11、B12共4枚B型彈;θ=25°時發射A1、A2、A3、A4、A5、A6共6枚A型彈;θ=35°時發射A7、A8、A9、A10、A11、A12共6枚A型彈,工況2的仿真結果如圖8～圖9所示。

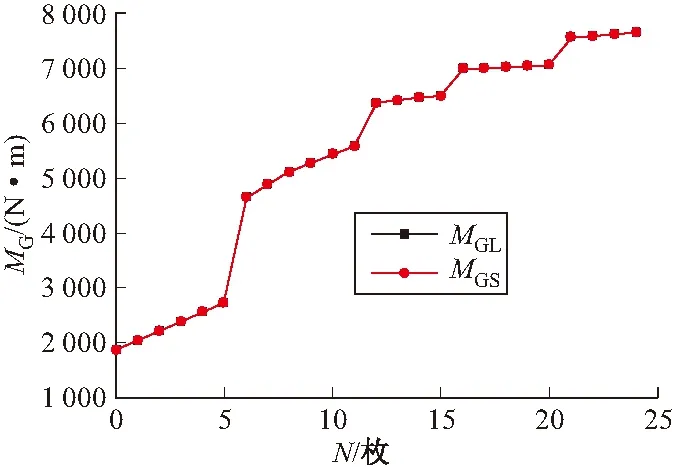
圖8 理論與實際結果對比

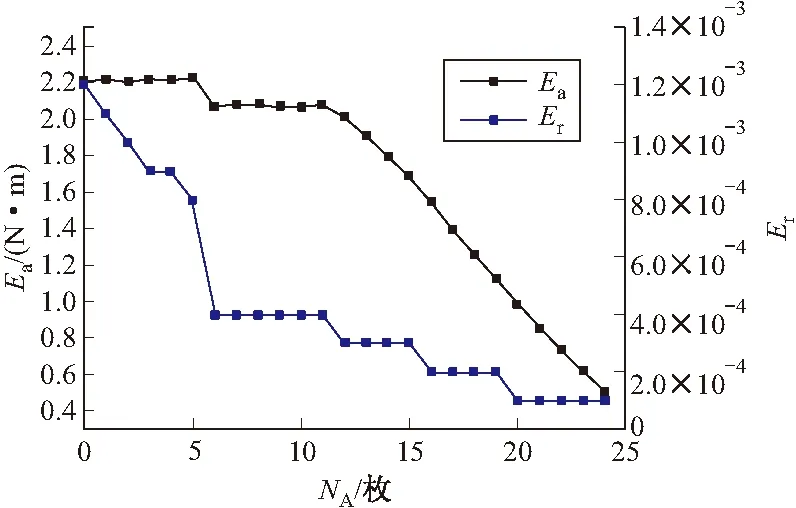
圖9 重力矩絕對誤差Ea與相對誤差Er

結果分析:曲線表明,在不同發射角下俯仰系統載彈模式改變時實際重力矩和理論重力矩大小基本一致,最大絕對誤差Ea,max=2.228 2N·m、最大相對誤差Er,max=0.12%<0.5%,滿足精度要求。

4 結論

文中以多管火箭炮武器系統為研究對象,為實時解算俯仰系統重力矩負載值,首先基于質點系等效質心原理推導出任意載彈模式下重力矩算法并采用Matlab編程實現,仿真結果表明:該算法精度高通用性好,解決了傳統研究中,使用Pro/E軟件測量俯仰系統裝配體重心位置,再計算重力矩中工作量大且通用性簡便性實時性差等不足。該算法可用于自適應重力矩平衡裝置控制系統負載解算單元,對后續俯仰系統自適應平衡裝置的研制有積極輔助意義。

[1] 原星武. 某自行導彈防空系統炮塔重力矩平衡技術 [C]∥第九屆全國雷達學術年會論文集, 2003: 976-978.

[2] 張鵬, 范樹遷, 石明全. 某扭桿式雙向平衡機設計及試驗分析 [J]. 機械設計與制造, 2011(2): 11-13.

[3] 黃朝學. 某扭桿式雙向平衡機的設計及疲勞壽命分析 [J]. 機械設計, 2010, 27(9): 72-75.

[4] 哈爾濱工業大學理論力學教研室. 理論力學 [M]. 7版. 北京: 高等教育出版社, 2009: 28-58.

[5] 同濟大學數學系. 高等數學 [M]. 6版. 北京: 高等教育出版社, 2007: 272-282.

[6] 鄭文緯, 吳克堅. 機械原理 [M]. 7版. 北京: 高等教育出版社, 1997: 69-76.

[7] 程永強, 韓勇. 某型導彈發射裝置平衡機的改裝設計 [J]. 軍事裝備測控技術, 2014, 22(5): 1469-1471.

[8] 方航, 王敏毅, 黃朝學. 某火箭彈發射裝置自適應平衡機原理方案研究 [J]. 艦船電子工程, 2015, 35(9): 51-55.

版 權 聲 明

凡稿件被本刊錄用，即視為作者同意將該論文的復制權、發行權、信息網絡傳播權、翻譯權、匯編權等權利在全世界范圍內轉讓給本刊。本刊已許可中文科技期刊數據庫(維普)、萬方數據數字化期刊群和中國知網(中國學術期刊(光盤版)電子雜志社)在其各自的系列數據庫產品中以數字化方式復制、匯編、發行及在信息網絡傳播本刊全文。作者著作權使用費和稿酬一并支付(即包括印刷版、光盤版和網絡版各種使用方式的報酬)。如作者對本聲明持有異議，請在投稿時說明。

本刊編輯部

Study on Gravity Moment Algorithm of Pitch System in Any Loading Mode

FANGHang,HUANGChaoxue,WANGMinyi

(No.710ResearchInstitute,CSIC,HubeiYichang443003,China)

Inordertocalculateloadofgravitymomentofacertaintypeofrocketlauncherinrealtime,basedontheprincipleofequivalentmasscenterofmassofaparticlesystem,themodelfunctionofgravitymomentinanyloadmodewasdeducedandprogrammedwithMatlab,andcomparedwithactualresultsmeasuredandcalculatedbyPro/Esoftware.Simulationresultsshowthatthiskindofalgorithmcansatisfyreal-timesolutionofgravitymomentinanyloadmode,settleseffectivelycurrentuseofPro/Esoftwaretomeasureandcalculategravitymomentmethodwhichhasseriesofshortcomingslikealargeamountofworkandpoorgenerality,whichcangreatlyimproveresearchefficiency.

arbitraryloadingpattern;rocketlauncher;gravitymoment;softwarealgorithm

2015-11-16

方航(1991-),男,湖北黃岡人,碩士研究生,主要研究:動力學與控制、嵌入式系統軟硬件設計。

TJ

A