幾何學概率的無線傳感器網絡能耗估計模型*

王昌征， 毛劍琳， 付麗霞， 郭 寧， 曲蔚賢

(昆明理工大學 信息工程與自動化學院，云南 昆明 650500)

?

幾何學概率的無線傳感器網絡能耗估計模型*

王昌征， 毛劍琳， 付麗霞， 郭 寧， 曲蔚賢

(昆明理工大學 信息工程與自動化學院，云南 昆明 650500)

針對無線傳感器網絡能耗這一問題，提出了一種基于幾何學概率的能耗估計模型。以節點的狀態轉換為基礎，建立了基于半Markov鏈的節點能耗模型，并引入概率分布函數的概念。從傳感器節點隨機分布出發，假定節點之間可以相互通信，分別對在單個正六邊形和相鄰兩個正六邊形內的節點隨機分布進行研究，推導得出能耗估計模型。仿真結果表明:該模型可以實現網絡能耗的準確估計。

無線傳感器網絡； 幾何學概率； 半Markov鏈； 概率分布函數； 能耗估計模型

0 引 言

隨著傳感技術、通信技術和計算機技術的飛速發展，無線傳感器網絡(wireless sensor networks,WSNs)日益受到國內外的高度重視[1]。WSNs和傳統的無線網絡有著很大的區別，傳感器節點體積較小[2]，自身裝載的能源也比較有限。此外，大多數WSNs節點一旦布置好就不會輕易的移動，因此,傳感器節點基本無法通過更換電池的形式來補充新的能源。大規模傳感器節點的部署是大勢所趨。因此，大規模傳感器網絡的能耗估計就顯得越來越重要，但是大規模WSNs的能耗估計存在較大的難度。通過一種簡易的方法對大規模傳感器網絡能耗進行估計，就顯得尤為重要。

在以前的研究中，已經有大量關于能耗估計的研究。文獻[3]提出了一種基于Markov鏈的休眠調度的能耗模型，文獻[4]考慮節點的發送和接收狀態建立能耗模型。文獻[5]考慮節點狀態的轉換，提出了基于半Markov鏈的WSNs能耗模型。文獻[6～9]通過研究表明，在正六邊形的幾何模型下對WSNs性能進行分析比在正方形和長方形的幾何模型下研究更加接近真實的情況。本文通過正六邊形幾何模型作為研究區域的方法，考慮節點的狀態，提出了一種能耗估計模型。模型的提出為大規模WSNs能耗的預測與估計提供了理論依據。

1 理論準備

文獻[10]給出了節點距離分布的概率分布函數的定義，推導得出了在單個正六邊形和相鄰兩個正六邊形的幾何模型下，節點距離分布的概率分布函數FD(d)和FTD(d)。

在WSNs通信的過程中，節點通信有一定的范圍。為了分析方便，假設節點的通信方式為任意節點可以通信。通過Matlab 2012a，在邊長L的單個正六邊形和兩個相鄰正六邊形中隨機撒點，通過蒙特卡羅的方法模擬結果，得到節點距離概率分布的擬合函數，如表1所示。

表1 概率分布擬合函數

圖1、圖2為任意節點通信情況在單個正六邊形和兩個相鄰正六邊形模型下撒點10 000個的概率分布函數的仿真結果。仿真結果證明了理論的正確性，節點距離分布的概率分布函數與實際的節點分布情況近乎一致。

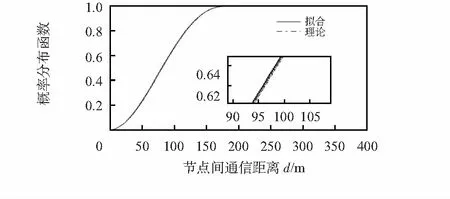
圖1 單個正六邊形概率分布函數Fig 1 Probability distribution function in single regular hexagon

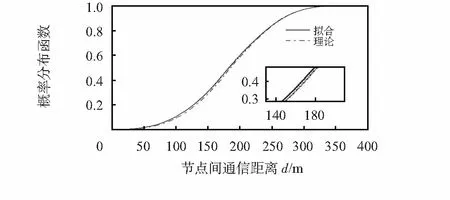
圖2 兩個相鄰正六邊形概率分布函數Fig 2 Probability distribution function in twoadjacent regular hexagon

2 能耗估計模型

為了研究方便，本文對能耗問題的研究設定如下：考慮節點分布區域邊界為單個正六邊形和兩個相鄰的正六邊形，節點通信方式為節點間相互通信。在此基礎上根據半Markov鏈的節點能耗模型，引入上文提到的節點分布的概率分布函數。推導出能耗估計模型，對能耗進行估計。能耗估計模型的建立為估算大規模網絡能耗提供了理論和現實依據。

2.1 基于半Markov鏈的節點能耗模型

在WSNs中，通信模塊共有發送態(transmission status,T)、接收態(receiving status,R)、空閑態(free status,F)、睡眠態(sleeping status,S)4種不同的狀態。4種狀態下節點消耗能量是不同的。在一定的時間范圍內節點的狀態切換是隨機的。這種概率的隨機性，正好滿足半Markov鏈的條件，因此本文引入半Markov鏈來建立節點的能耗模型。如圖3所示，為節點的4種狀態的轉換圖。通過該轉換圖，可以看出，4種狀態相互轉換的具體關系。這里規定P(i)為傳感器節點在狀態i下的概率。

圖3 傳感器節點狀態轉換圖Fig 3 State transition diagram of sensor node

根據圖3的狀態轉移的描述，可以用狀態轉移矩陣來描述這個轉移的過程。設P為狀態轉移矩陣，得出WSNs中節點狀態的轉移矩陣P的表達式為

(1)

由于傳感器節點在睡眠狀態，不可能直接變為接收和發送狀態，以此概率P(S|T)和P(S|R)為0。在轉換時間t=nT內，傳感器節點經歷了n次轉換，在n→∞時，無線傳感器網絡的狀態轉移概率為

(2)

式中P1,1,P2,2,P3,3,P4,4為節點在S態、T態、R態和F態4種狀態下的穩態概率,且規定節點在這4種狀態下消耗的能耗功率為PS，PT，PR和PF。那么可以求得在t=nT時間內的傳感器節點能耗功率為

(3)

文獻[11]指出，這4種狀態的功耗比約為2 000∶400∶400∶1，所以,要降低網絡的能耗，其關鍵就是使得盡可能多的節點處于睡眠狀態。本文首先考慮節點處于發送信息狀態(其余狀態可依據比例求得)，且其數學模型選用文獻[11]的網絡通信能量模型

ET=(α+βdm)·L

(4)

式中ET為節點發送信息所需的能量；L為所發數據的長度；d為節點之間的通信距離；m為信號的消減因子；α為傳輸一比特信息所需的能量 (包括啟動時消耗的能量)；β為傳輸過程中單位能量的損耗。

將式(4)兩邊同除以時間t，則有

PT=(α+βdm)·v

(5)

式中PT為能耗功率，J/s；v為數據傳輸速率，即無線信號比特率。式(5)中各參數值由具體的應用來確定，在簡化分析時,可以取典型值。一般取值如下α=50 nJ/bit，β=0.001 3 pJ/bit/m4，m=4，v=10 kB/s。

又根據式(3)和式(5)，可以求得在t=nT時間內的傳感器節點能耗功率為

P=t×(5×10-4P1,1PT+P2,2PT+0.2P3,3PT+0.2P4,4PT)

=t×(5×10-4P1,1+P2,2+0.2P3,3+0.2P4,4)×(α+

βdm)·v

(6)

2.2 能耗估計函數

節點的模擬能耗概率分布函數，以節點的距離為研究對象，得到一個能耗估計函數，以此來估計無線傳感器網絡的能耗。為了研究方便，定義如下：

定義1 能耗估計函數估計的能耗為：在節點都可以相互通信條件下，節點的總能耗。

定義2 節點距離的數學期望近似等于節點平均距離。

對概率分布函數FD(d)和FTD(d)求導可以得到概率密度函數fD(d)和fTD(d),則在單個正六邊和兩個相鄰正六邊形內隨機播撒N個節點，節點距離的數學期望為

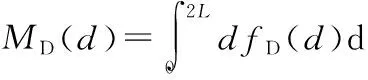
(7)

(8)

根據上述式(7)、式(8)，可以得到N個節點的所有分布距離和的近似公式，如式(9)和式(10)所示

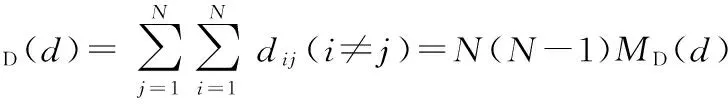
≈N(N-1)×0.826 254 277 5L

(9)

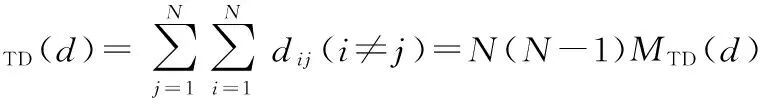
≈N(N-1)×1.858 336 696 6L

(10)

由此，可以推導出能耗估計函數得到函數的定義，如下：

定義4 設在單個正六邊形或者兩個相鄰正六邊形區域Ω中，隨機撒點N個。任意節點可以相互通信，那么通過節點距離的期望來估計所有節點產生總能耗的函數為能耗估計函數，計算公式如下所示

P～D(d)=t×(5×10-4P1,1PT+P2,2PT+0.2P3,3PT+

0.2P4,4PT)

=t×(5×10-4P1,1+P2,2+0.2P3,3+0.2P4,4)×

(α+β(d～D(d))m)·v

(11)

P～TD(d)=t×(5×10-4P1,1PT+P2,2PT+0.2P3,3PT+

0.2P4,4PT)

=t×(5×10-4P1,1+P2,2+0.2P3,3+0.2P4,4)×

(α+β(d～TD(d))m)·v

(12)

式(11)為單個正六邊形內能耗估計函數；式(12)為單個正六邊形內能耗估計函數。上述公式可以快速、準確的估計無線傳感器網絡的總能耗。

這里通過仿真證明該模型的準確性，為此定義一個誤差公式，如式(13)和式(14)所示，通過誤差值的大小來證明能耗估計模型的準確性

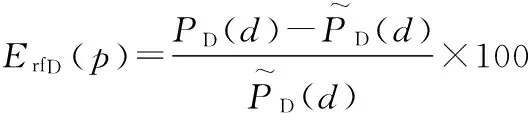
(13)

(14)

式中PD(d)為單個正六邊形內實際總能耗，ErfD(p)為誤差；PTD(d)為兩個相鄰正六邊形內實際總能耗，ErfTD(p)為誤差。

3 仿真驗證與分析

3.1 仿真驗證

假設各個傳感器節點處于相互通信狀態，在Matlab R2012a中，根據式(11)和式(12)，對能耗估計模型進行仿真，網絡能耗仿真參數如表2所示。

在邊長L=100 m的單個正六邊形內和相鄰兩個正六邊形內，在時間t=200 s，通過模特卡羅法對能耗估計函數對實際情況進行擬合，圖4、圖5為能耗估計函數以及擬合圖。而且取節點個數N為3 000個，取t為200,400,600,800,1 000 s時，在邊長L=100 m的單個正六邊和兩個相鄰正六邊形內，求出仿真的網絡擬合總能耗、能耗估計值和誤差值。進一步證明能耗估計模型的正確性，網絡能耗對比如表3所示。

表2 網絡能耗仿真參數

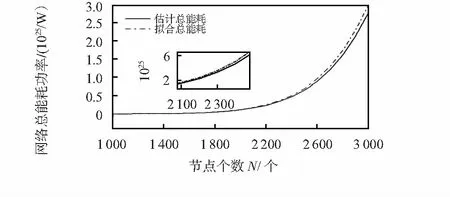
圖4 單個正六邊形能耗估計函數Fig 4 Energy consumption estimation function in singleregular hexagon

圖5 兩個相鄰正六邊形能耗估計函數Fig 5 Energy consumption estimation function in two adjacent regular hexagon

參數t=200st=400st=600st=800st=1000sPD(d)2.7864×10265.5743×10268.3602×10261.1151×10271.3942×1027P～D(d)2.7800×10265.5600×10268.3400×10261.1120×10271.3900×1027PTD(d)7.1117×10271.4224×10282.1336×10282.8448×10283.5560×1028P～TD(d)7.0844×10271.4169×10282.1253×10282.8338×10283.5422×1028ErfD(p)%0.2360.2570.2420.2790.300ErfTD(p)%0.3840.3850.3910.3880.389

3.2 仿真結果分析

從圖4、圖5的能耗估計函數的仿真圖可以看出，除少數變化比較大的點以外，能耗估計模型非常接近擬合能耗函數，證明了能耗估計模型的準確性。從表3實際的參數值可以看出,能耗估計值與擬合值之間的誤差小于1 %，這也進一步證明了能耗估計模型的準確性。由此，可以有效估計WSNs的總能耗。

4 結束語

本文在研究了單個正六邊形和相鄰兩個正六邊形內網絡能耗與節點間距離的關系。本文先對Zhuang和Pan的距離分布函數的基礎上利用蒙特卡洛法驗證了節點距離概率分布函數的正確性，然后根據半Markov鏈的節點能耗模型，引入節點距離概率分布函數，推導出了能耗估計函數。然后利用Matlab 2012a仿真得出了估計能耗估計函數與擬合能耗的仿真圖，給出了節點數N為3 000個，取t為200,400,600,800,1 000 s時，在邊長L=100 m的單個正六邊和兩個相鄰正六邊形內，求出網絡擬合的總能耗、能耗估計值和誤差值,證明了能耗估計模型的有效性。該模型的提出為WSNs能耗的分析，為WSNs的節點配置提供了依據。在后繼的工作中，將基于幾何學概率進一步研究大規模WSNs的干擾和容量等問題。

[1] 謝和平,周海鷹,左德承，等.無線傳感器網絡能量優化與建模技術綜述[J].計算機科學,2012,39(10):15-20,25.

[2] 陳 英,舒 堅,陳宇斌,等.無線傳感器網絡技術研究[J].傳感器與微系統,2007,26(10):1-4，8.

[3] Shi Z S,Wang C F,Zheng P,et al.An energy consumption prediction model based on GSPN for wireless sensor networks[C]∥2012 the Fourth International Conference on Computational and Information Sciences,Chongqing,China:IEEE,2010:1001-1004.

[4] 王淑華,陳國定,趙國炳.一種無線傳感器網絡能耗模型及有效性分析[J].計算機應用與軟件,2011,28(2):215-217.

[5] 魏 銳,藺 莉.基于半馬爾科夫鏈的無線網絡能耗模型的研究[J].電子技術應用,2015,41(4):112-115.

[6] Zhuang Y,Pan J,Cai L.Minimizing energy consumption with probabilistic distance models in wireless sensor networks[C]∥The 29th IEEE International Conference on Computer Communications,San Diego,CA,USA:IEEE,2010:2453-2461.

[7] Zhuang Y,Luo Y,Pan J,et al.A geometric probability model for capacity analysis and interference estimation in wireless mobile cellular systems[C]∥The 54th Global Telecommunications Conference,Houston,USA:IEEE,2011:1-6.

[8] Baltzis K B.A geometric method for computing the nodal distance distribution in mobile networks[J].Progress in Electromagnetics Research,2011,114:159-175.

[9] Baltzis K B.Analytical and closed-form expressions for the distribution of path loss in hexagonal cellular networks[J].Wireless Personal Communications,2010,60(4):599-610.

[10] Zhuang Y,Pan J.A geometrical probability approach to location-critical network performance metrics[C]∥IEEE International Conference on Computer Communications,Munich,Germany:IEEE,2012:1817-1825.

[11] 胡風華.基于節點均勻分布的無線傳感器網絡能耗研究[D].淮南:安徽理工大學,2013.

毛劍琳，通訊作者，E—mail:km_mjl@aliyun.com。

Energy consumption estimation model for WSNs based on geometrical probability*

WANG Chang-zheng, MAO Jian-lin, FU Li-xa, GUO Ning, QU Wei-xian

(Faculty of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China)

Aiming at problem of energy consumption in wireless sensor networks(WSNs),propose an energy consumption estimation model based on geometric probability approach.This model establishes a model for node energy consumption based on semi-Markov chain on the basis of conversion of node state, and introduce the concept of probability distribution function.Start from random distribution of sensor nodes,assume that nodes can communicate with each other and research on random distribution of nodes in single regular hexagon and two adjacent hexagonals.Derive and obtain energy consumption estimation model.Simulation results shows that the proposed model can achieve accurate estimation of energy consumption of WSNs.

wireless sensor networks(WSNs); geometrical probability; semi-Markov chain; probability distribution function; energy consumption estimation model

10.13873/J.1000—9787(2016)12—0037—04

2016—02—24

國家自然科學基金資助項目(61163051); 云南省應用基礎研究基金資助項目(2009ZC050M)

TP 393

A

1000—9787(2016)12—0037—04

王昌征(1990-)，男，山東青島人，碩士研究生，主要研究方向為無線傳感器網絡覆蓋。