約束非線性系統穩定經濟模型預測控制

何德峰

約束非線性系統穩定經濟模型預測控制

何德峰1

考慮約束非線性系統,提出一種新的具有穩定性保證的經濟模型預測控制(Economic model predictive control, EMPC)策略.由于經濟性能指標的非凸性和非正定性,引入關于經濟最優平衡點的正定輔助函數.利用輔助函數的最優值函數定義原始EMPC優化問題的穩定性約束.應用終端約束集、終端代價函數和局部控制器三要素,建立閉環系統關于經濟最優平衡點的漸近穩定性和漸近平均性能.進一步,結合多目標理想點概念,將提出的控制策略用于多個經濟性能指標的優化控制,得到穩定多目標EMPC策略.最后,以連續攪拌反應器為例,比較仿真結果驗證本文策略的有效性.

模型預測控制,非線性系統,經濟優化,穩定性,多目標控制

近年來,經濟模型預測控制(Economic model predictive control,EMPC)在學術界和工業界受到了廣泛關注[1?15].EMPC的一個顯著優點是將過程實時控制與經濟性能優化集成在一個最優控制的框架內設計[1?2].不同于傳統MPC(Model predictive control)需要預先設定目標值為前提(故也稱為目標跟蹤型MPC)[1],EMPC原則上并不需要這樣一個前提[2].由于這類MPC性能函數通常與過程的經濟(環保)性能相關,故統稱為經濟MPC.但該“經濟”并不特指某個經濟性能,而泛指一類非正定和(或)非凸的任意性能函數.盡管如此,經濟MPC和傳統MPC的實施機理一樣,即都采用滾動時域方式實現系統的閉環狀態(或輸出)反饋控制[1?3],但直接優化經濟性能計算控制量給EMPC帶來更復雜的穩定性問題[1,16].

常規EMPC穩定性需引入強對偶性或耗散性假設,并附加罰函數將經濟性能函數轉換為正定性能函數,再結合終端等式或不等式約束,建立EMPC的遞推可行性和閉環穩定性[4?8,16?17].由于系統與性能函數不一定滿足正則性(Regulation)條件[6],約束非線性系統通常不滿足對偶性與耗散性假設[4].進一步,由于附加項通常是平衡點偏差的函數,將改變原經濟性能的最優路徑,影響原始經濟性能,特別是終端等式約束加重了EMPC在線優化的計算量,同時會減小EMPC的吸引域.針對終端約束對經濟性能的影響,文獻[18]應用耗散性和能控性假設建立了無終端約束EMPC穩定性,但要求預測時域足夠大,而這將增加EMPC在線優化的計算量.基于能控性假設和切換控制思想,文獻[19]提出了基于Lyapunov函數的穩定EMPC策略,但為保證閉環系統的穩定性和漸近平均性能,需要在線求解三個非線性最優控制問題[20],增加了EMPC運行的復雜性.現有研究結果表明, EMPC的經濟性能與穩定性存在一定的矛盾[7,16].如何在優化經濟性能的同時確保閉環系統的穩定性是EMPC研究的一個關鍵問題.

另一方面,在工業過程經濟目標優化操作中,通常存在多個相互矛盾的性能指標[21?22],且這些性能指標具有不同的物理含義.因為加權函數法使用簡單,在控制實踐中,通常被用來近似處理多目標優化控制問題.但各目標加權系數的選擇與整定需要通過大量的離線實驗完成,特別是在系統約束和目標函數非凸的情況下,權值選擇與整定會異常困難[22?23].近年來,提出了一些新的多目標優化MPC設計,如基于穩態目標規劃計算的雙層多目標MPC[23]、參數規劃多目標線性MPC[24]、混合邏輯整數規劃多目標MPC[25?27]、考慮性能指標優先級要求的多目標MPC[28?30]以及基于多目標理想點跟蹤的多目標MPC[31?32]等.由于理想點跟蹤多目標MPC策略不需要人為選擇各性能的加權系數,在不需要系統先驗知識的條件下能自動處理各個性能指標的沖突性,成為目前廣受關注的一種多目標MPC策略.但在理想點跟蹤多目標MPC中,由于性能指標相互沖突,折中性能函數在穩態平衡點不為零,即折中性能函數不是穩態平衡點的正定函數,對應的控制器通常不穩定,因此可看作是一類特殊的EMPC問題,可采用EMPC方法建立理想點跟蹤多目標MPC的閉環穩定性.

本文考慮具有狀態和控制約束的非線性系統,提出一種新的具有遞推可行性和穩定性保證的EMPC策略.通過離線計算經濟性能指標的最優平衡點,引入關于該點偏差的正定輔助函數.利用輔助函數的最優值函數定義原始EMPC優化問題的一個穩定性約束.再應用終端約束集、終端代價函數和局部控制器等三要素[3],建立閉環系統關于經濟最優平衡點的漸近穩定性和漸近平均性能.與現有穩定EMPC策略相比,本文的一個主要創新點是EMPC的遞推可行性和漸近穩定性與非線性系統的強對偶性、耗散性條件無關,從而簡化EMPC策略的設計.進一步，結合多目標理想點法[31],將上述結果推廣至多個經濟性能指標的優化控制問題,提出一種新的具有穩定性保證的理想點跟蹤多目標EMPC策略.最后以連續攪拌反應器多目標控制為例,對比仿真驗證本文結果的有效性.

符號說明:集合R≥0和I≥0分別表示非負實數集和非負整數集.Ia:b={i∈I≥0:a≤i≤b},其中a∈I≥0和b∈I≥0.符號uk表示k∈I時刻的一個信號序列,系統在k∈I≥0時刻的狀態為系統在零時刻的狀態.給定一個向量符號T表示的轉置,表示的p范數,表示在第k時刻對

未來第k+i時刻的預測變量.

1 問題描述

考慮離散時間非線性系統

考慮經濟性能函數Le:X×U→R.該函數關于連續且有界,但可能是非凸的且對于任意不一定是正定的.由文獻[16]可知,極小化這類性能函數的控制律不一定保證閉環系統漸近穩定,甚至出現震蕩和周期響應.盡管周期響應適用一些間歇工業過程,但大部分連續工業過程要求閉環系統是漸近穩定的.本文目標是設計一個經濟最優狀態反饋控制律使閉環系統能漸近穩定于最優經濟平衡點同時滿足系統狀態和控制約束(2),以及漸近平均性能條件

2 穩定經濟預測控制

2.1 預測控制器

令N∈I≥1為預測時域,定義k時刻的N步預測控制序列和對應預測狀態序列給定緊集XT?X,如果uk滿足?i∈I0:N?1,以及和則該控制序列稱為系統(1)的一個可行預測控制序列.

考慮系統(1)的一個可行預測控制序列uk及其對應的預測狀態序列xk,定義如下目標函數:

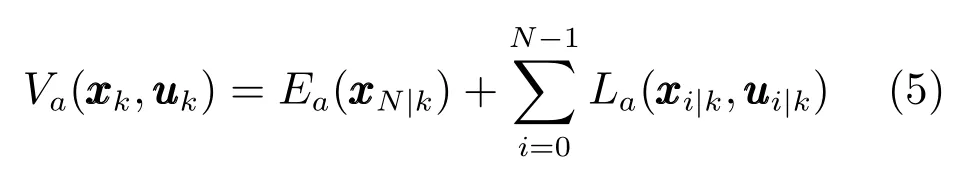
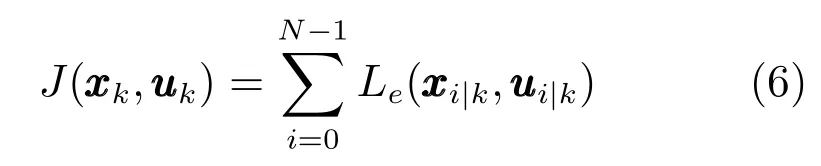
為計算EMPC控制律,在每個時刻求解如下有限時域最優控制問題

如果優化問題(7)在k時刻是可行的,則根據滾動時域控制原理,定義經濟預測控制律如下:

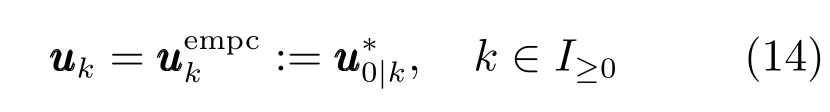
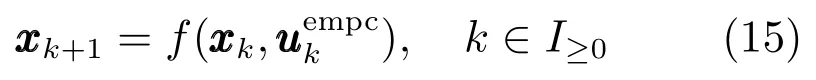
本文將證明值函數(9)是系統(15)的Lyapunov函數,建立閉環系統關于的漸近穩定性結論.

算法1.(EMPC算法)

2.2 穩定性與平均性能

顯然,XN滿足XT?XN?X,且XN?XN+1.

定理1.如果假設1和2成立,則對于任意給定α≥0,優化問題(7)在XN內具有遞推可行性,進而XN是閉環系統(15)的一個不變集.

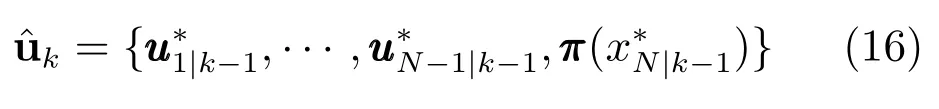
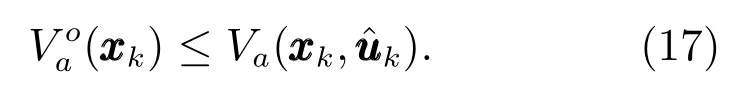
進一步考慮控制序列(16),可得:

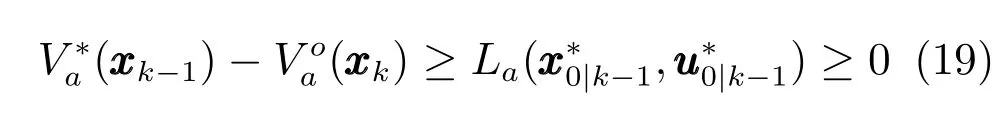
定理2.如果假設1和2成立,且優化問題(7)在初始時刻存在可行解.給定α∈[0,1),則是閉環系統(15)在XN內的漸近穩定平衡點,且XN是閉環系統的一個吸引域.

證明.任意給定α∈[0,1),由于優化問題(7)在初始時刻是可行的.根據定理1可知,該優化問題在任意k時刻存在可行解.

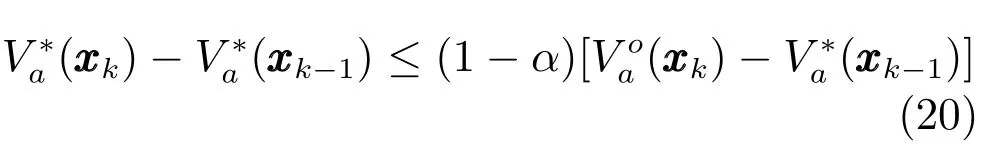
考慮假設1和2,將式(19)代入不等式(20)并整理得:

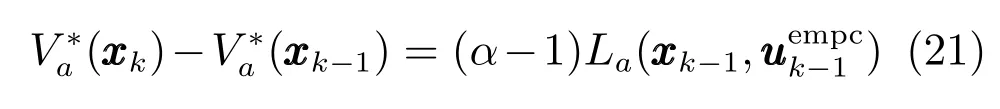
注3. 由定理2證明過程可知,閉環系統(15)的穩定性是通過不等式(7e)建立的,即利用(Ea,XT,π)滿足假設1和2,使函數(9)成為閉環系統的Lyapunov函數,因此式(7e)是一類基于Lyapunov函數的穩定性約束.在常規的基于Lyapunov函數MPC策略[1,38]中,性能函數是關于平衡點偏差的正定函數,故Lyapunov穩定性約束是通過強制一個已知的正定函數的導數小于零構造的,而本文采用MPC的三要素原理建立閉環系統的Lyapunov函數,因此是兩種不同的穩定性約束條件.其次,經濟優化問題(7)的最優解并不能保證是優化問題(8)的最優解,而通常只是一個可行解;同理,盡管是優化問題(8)的最優解,但只是優化問題(7)的一個可行解.盡管如此,結合定理1和MPC三要素原理可得,由最優解定義的滾動時域控制器同樣能保證的漸近穩定性,且XN是對應閉環系統的一個吸引域.最后,控制序列(16)只是優化問題(8)的一個可行序列,但不一定是優化問題(7)的可行序列,因為不等式(17)使得序列(16)不一定滿足約束(7e).

定理3.如果假設1和2成立,且優化問題(7)在初始時刻存在可行解.如果給定α∈[0,1),則閉環系統(15)在吸引域XN內滿足漸近平均性能(3).

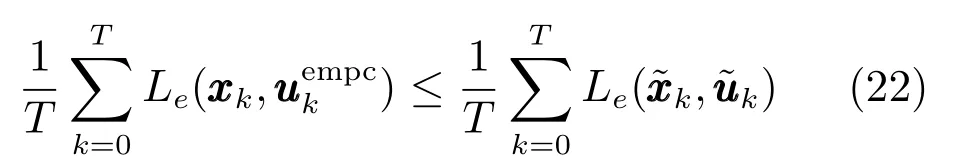
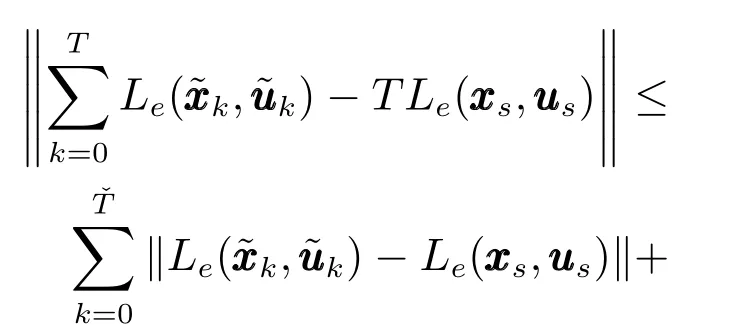
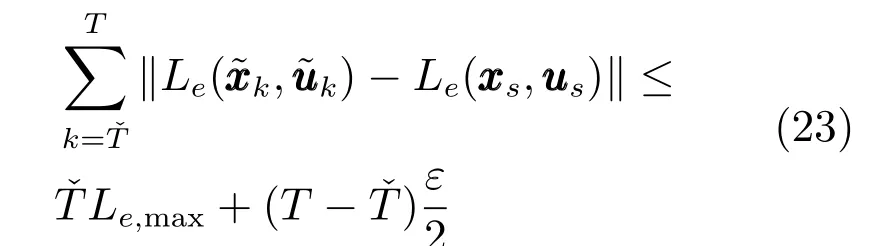
即任意充分小ε＞0,總存在一個有限時間T?,當T＞T?時,式(24)成立.從而由極限理論可知,

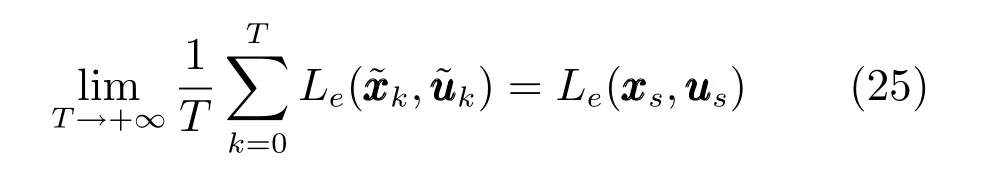
結合式(25),對式(22)兩邊同時取極限,可得:

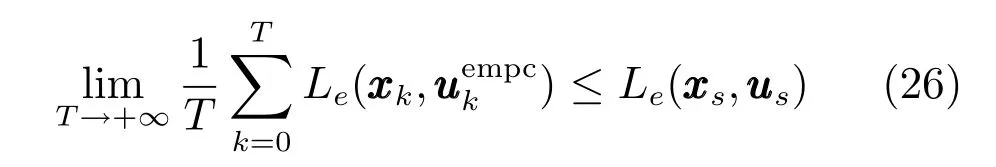
即閉環系統(15)在XN內具有漸近平均性能. □

注 4.閉環系統的漸近平均性能(26)是建立在無窮時間域上的結果,因此,在任意一個有限時間區間的平均性能值不一定小于穩態經濟性能

3 一類多目標經濟預測控制

上述穩定EMPC策略可以推廣應用到多經濟目標優化控制問題.本節結合多目標理想點概念[39],給出一種穩定多目標EMPC策略.

3.1 多目標理想點

考慮l∈I≥2個連續且有界的性能函數Lj: X×U → R,j∈I1:l.令為函數向量.在多目標優化問題中,這些性能函數可能相互沖突,此時不存在唯一的最優解同時極小化各個性能函數j∈I1:l.通常采用Pareto最優解定義多目標優化問題的有效解,但Pareto最優解通常不唯一(甚至無窮多個),并在目標空間Rl形成一個Pareto面(Pareto front)[39].因此,文獻[28–30]等對具有優先級排序的多目標優化控制問題,采用字典序多目標優化方法設計多目標MPC控制器;而文獻[31–32]等對一類沖突但無排序要求的多目標優化控制問題,提出了理想點跟蹤多目標MPC控制器設計等.

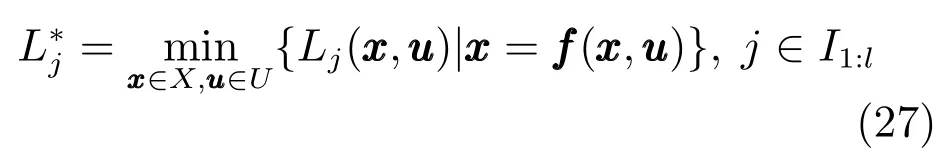
其中,向量p范數‖·‖p定義了目標空間中性能值到理想點L?的距離.則本節的目的是設計一個多目標狀態反饋控制器使閉環系統在約束(2)作用下能漸近穩定于Pareto解同時極小化一組性能函數為此,結合算法1和多目標理想點法,設計一種理想點跟蹤多目標優化經濟模型預測控制器.

3.2 多目標EMPC

下面給出多目標EMPC控制律(30)的實施步驟.

算法2.(多目標EMPC算法)

1)系統在吸引域XN內漸近穩定于

2)系統在XN內滿足如下性能:

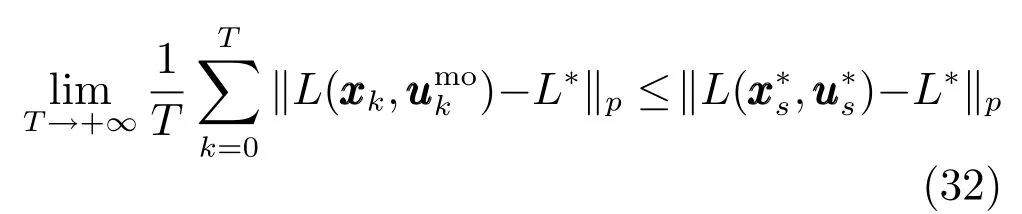
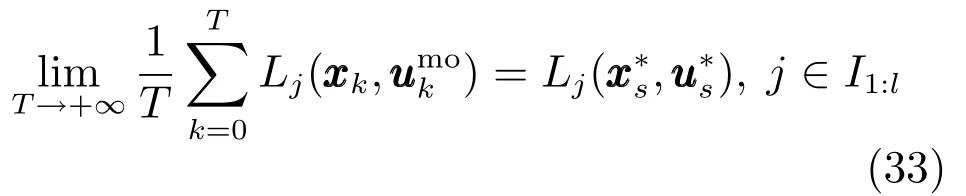
證明.考慮性能函數(29),并利用定理1～3的結果直接得到定理4. □

4 實例仿真

考慮二元物系聚合過程連續攪拌釜反應器[38],其動態聚合過程可描述為

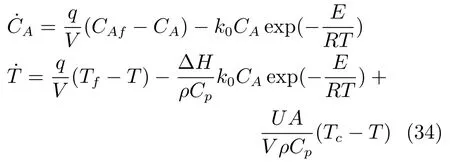
其中,CA、T和Tc分別為反應物濃度(mol/L)、反應器溫度(K)和冷卻劑溫度(K),模型參數為q=100 L/min,CAf=1 mol/L,UA=5×104J/min·K,ρ=1000 g/L,Cp=0.239 J/g·K, E/R=8750 K,k0=7.2×1010min?1,V=100 L,Tf=350 K,△H=?5×104J/mol.定義狀態變量和控制變量u=Tc,及狀態和控制約束

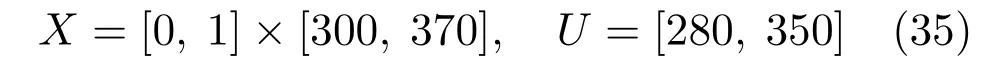
我們用多目標優化控制結果驗證本文結果的有效性.

在聚合反應過程中,通常希望增強聚合反應速率以提高生產效率,即極小化性能函數

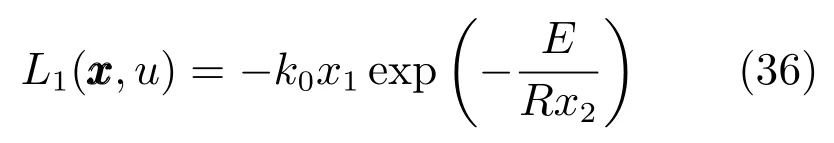
同時希望降低能源消耗,采用極小化性能函數

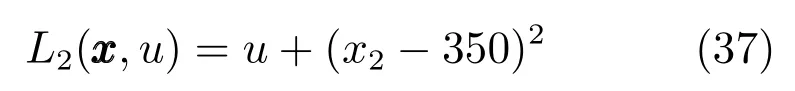
表示降低能源消耗.因此,一個理想的聚合反應過程控制器應該同時滿足上述兩個性能要求.

選擇向量2-范數,定義折中經濟性能函數

可以驗證,三要素(40)滿足假設1和2.

在仿真中,采用歐拉差分法離散系統(34),取采樣周期為0.1 min,預測步長N為7,仿真總步長為30.采用MatLab 2007的fmincon函數優化計算最優控制問題(7)和(8).下面,先驗證本文結果的正確性,再與文獻[6]等提出的EMPC策略、常規目標跟蹤型MPC策略做比較以驗證本文結果的優越性.

4.1 仿真實驗一

選取系統初始狀態(0.7 mol/L,320 K),運行算法2,仿真結果如圖1所示.其中,實線為α=0的仿真結果;虛線為α=0.3的仿真結果;點劃線為α=0.7的仿真結果;點線為α=0.99的仿真結果.需要指出的是:為了更清楚地顯示值函數在不同α取值時的差異,圖1右下子圖的時間坐標截取為前20步.由圖1可知,對于系數α∈[0,1),值函數都是單調遞減的.因此,由算法2產生的多目標EMPC及其閉環系統漸近穩定于Pareto最優穩態解且在所有時刻滿足狀態和控制約束(35).

盡管對系數α∈[0,1),閉環系統漸近穩定,但不同值對應的閉環系統的動態響應和經濟性能是不一樣的,圖2給出了上述取值時的性能實時曲線.分析圖1和2可知,α取值越小,值函數下降越快,閉環系統趨于最優平衡點的時間越短,但經濟性能可能會下降,如圖2左子圖實線所示.反之亦然,如對應α=0.99的點線所示,盡管在30步仿真時間內,閉環系統還沒有收斂至平衡點,但它的性能指標L1可以達到更小的值.因此,設計者可以通過調整α取值對閉環系統的收斂速度和經濟性能進行權衡,從而提高經濟預測控制器應用的靈活性.

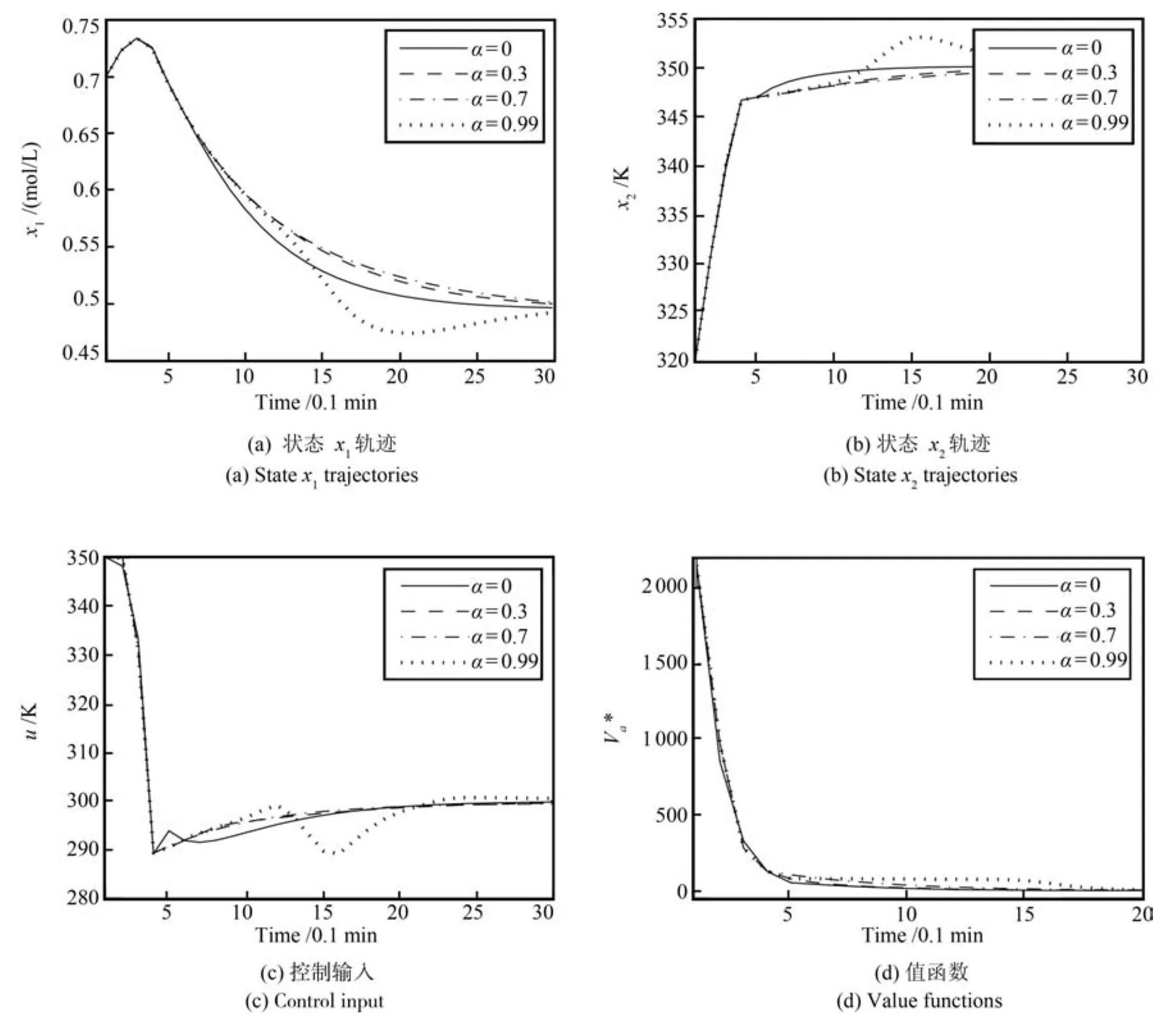
圖1 狀態軌跡、控制輸入和值函數曲線Fig.1 Profiles of states,control and value functions

4.2 仿真實驗二

為驗證本文控制策略的優越性,對比文獻[6]等提出耗散EMPC策略(簡記為D-EMPC)和目標跟蹤MPC策略(簡記為T-MPC).由于T-MPC策略的性能函數總是設定值偏差的正定函數[1?2],因此在該次實驗中,令正定函數(39)為T-MPC策略的性能函數.考慮初始狀態(0.7 mol/L,320 K),圖3給出了本文策略和其余兩種策略在相同仿真環境下的控制結果.其中,實線表示本文策略(α=0.2)對應結果;點線表示D-MPC策略對應結果;虛線表示T-MPC策略對應結果;右下子圖符號“*”表示性能理想點,“o”表示最優平衡點對應的經濟性能.

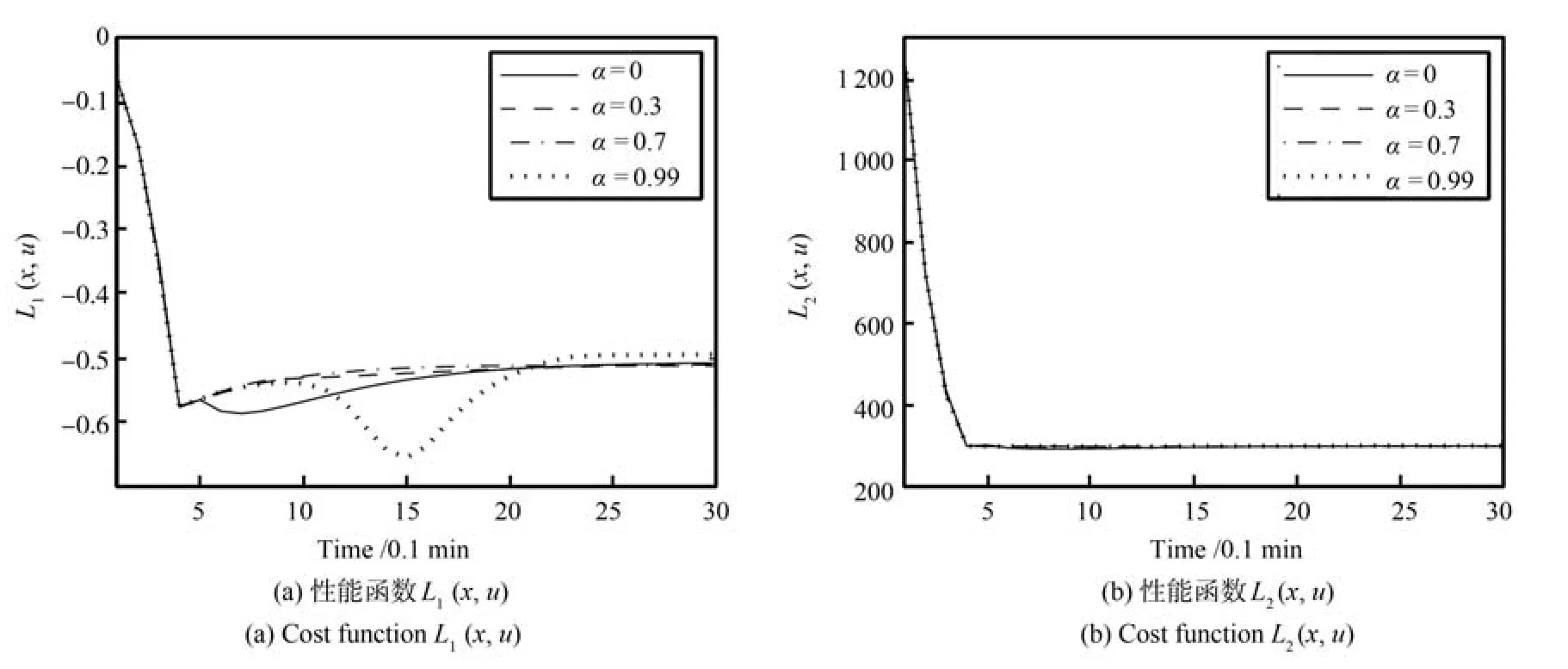
圖2 性能函數實時曲線Fig.2 Real-time profiles of cost functions

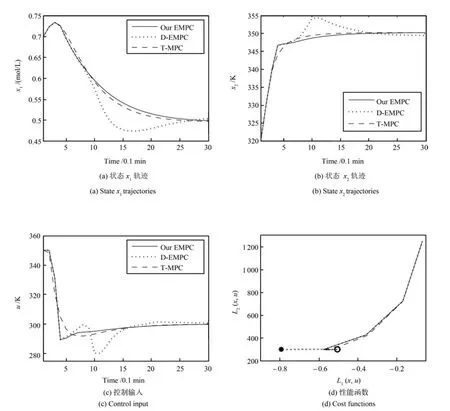
圖3 狀態軌跡、控制輸入和性能函數相位曲線Fig.3 Profiles of states,control,and cost functions

由圖3分析可知,本文策略和T-MPC策略對應的閉環系統漸近收斂至而D-MPC策略對應的閉環系統在暫態響應過程中出現震蕩現象(如控制輸入u),同時存在穩態誤差(如反應器溫度x2),這主要是因為D-EMPC策略要求被控系統和經濟性能函數滿足嚴格耗散性條件.但對于非線性系統,嚴格耗散性條件很難成立[5],如本例中的聚合過程(34)和經濟性能(38)不滿足嚴格耗散性條件,從而D-EMPC策略不能保證閉環系統收斂至對應的性能相位曲線也不能收斂至最優平衡點對應的經濟性能“o”,如圖3右下子圖點線所示.另一方面,盡管本文策略和T-MPC策略的閉環系統都收斂至但收斂路徑不一樣.如果以進入穩態解±5%為界,那么本文策略對應閉環系統的收斂過渡時間小于T-MPC策略閉環系統的收斂過渡時間,從而加快閉環系統的過渡響應過程.

令Av{L1}和Av{L2}分別表示性能函數(36)和(37)的漸近平均性能,則進一步比較三種策略取得的漸近平均性能.取足夠大的仿真時間步長100,圖4和表1分別給出了三種策略關于性能函數(36)和(37)的瞬時性能和漸近平均性能.圖4中實線為本文策略對應的結果;點線為D-MPC策略對應的結果;虛線表示T-MPC策略對應結果.由圖4分析可知,對于本文策略和T-MPC策略取得的平均性能較優于D-MPC策略;對于三種策略取得的平均性能較為接近.進一步,以D-MPC策略取得的漸近平均性能值作為參考基準,對于本文策略和T-MPC策略分別增效1.52%和1.69%;對于本文策略和T-MPC策略分別增效0.34%和0.27%.綜合圖3和4和表1結果,驗證了本文策略在性能優化方面的優越性.

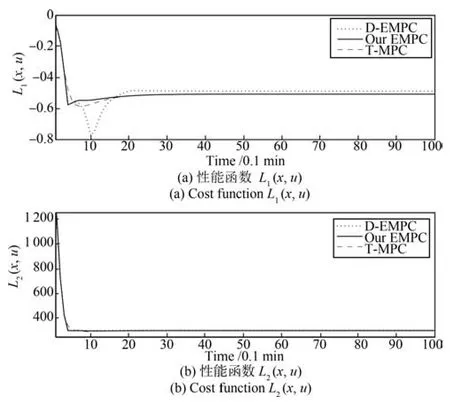
圖4 性能函數的瞬時值曲線Fig.4 Real-time value profiles of cost functions

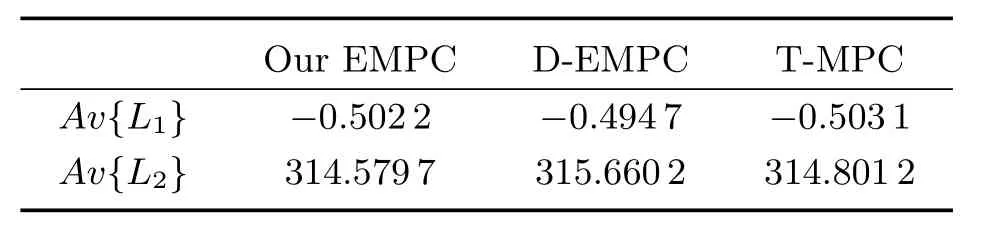
表1 漸近平均性能Table 1 Asymptotic average performance

5 結語

本文針對約束非線性系統,提出了一種新的穩定經濟MPC策略.通過引入關于經濟最優平衡點的輔助正定函數,并利用輔助函數的最優值函數定義原始EMPC優化問題的一類穩定性約束.應用常規MPC的終端約束集、終端代價函數和局部控制器三要素方法,建立了閉環系統關于經濟最優平衡點漸近穩定性和漸近平均性能的充分條件.結合多目標理想點法,將提出EMPC策略推廣至多經濟目標函數優化控制問題.建立了多目標EMPC策略的漸近穩定性充分條件.通過對連續攪拌反應器多目標優化控制的對比研究,驗證了本文結果的有效性.

1 Ellis M,Durand H,Christofides P D.A tutorial review of economic model predictive control methods.Journal of Process Control,2014,24(8):1156?1178

2 Tran T,Ling K V,Maciejowski J M.Economic model predictive control—a review.In:Proceedings of the 31st International Symposium on Automation and Robotics in Construction.Sydney,Australia:IAARC,2014.35?42

3 Mayne D Q.Model predictive control:recent developments and future promise.Automatica,2014,50(12):2967?2986

4 Angeli D,Amrit R,Rawlings J B.On average performance and stability of economic model predictive control. IEEE Transactions on Automatic Control,2012,57(7): 1615?1626

5 Diehl M,Amrit R,Rawlings J B.A Lyapunov function for economic optimizing model predictive control.IEEE Transactions on Automatic Control,2011,56(3):703?707

6 Amrit R,Rawlings J B,Angeli D.Economic optimization using model predictive control with a terminal cost.Annual Reviews in Control,2011,35(2):178?186

7 Fagiano L,Teel A R.Generalized terminal state constraint for model predictive control.Automatica,2013,49(9): 2622?2631

8 Ferramosca A,Limon D,Camacho E F.Economic MPC fora changing economiccriterion forlinearsystems. IEEE Transactions on Automatic Control,2014,59(10): 2657?2667

9 Huang R,Harinath E,Biegler L T.Lyapunov stability of economically oriented NMPC for cyclic processes.Journal of Process Control,2011,21(4):501?509

10 Chu B,Duncan S,Papachristodoulou A,Hepburn C.Using economic model predictive control to design sustainable policies for mitigating climate change.In:Proceedings of the 51st IEEE Conference on Decision and Control.Maui, HI:IEEE,2012.406?411

11 Hovgaard T G,Larsen L F S,J?rgensen J B.Flexible and cost efficient power consumption using economic MPC a supermarket refrigeration benchmark.In:Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference.Orlando,FL:IEEE,2011. 848?854

12 Ma W J,Gupta V.Desynchronization of thermally-coupled first-order systems using economic model predictive control. In:Proceedings of the 51st IEEE Conference on Decision and Control.Maui,HI:IEEE,2012.278?283

13 Lao L F,Ellis M,Christofides P D.Economic model predictive control of parabolic PDE systems:addressing state estimation and computational efficiency.Journal of Process Control,2014,24(4):448?462

14 Lao L F,Ellis M,Christofides P D.Smart manufacturing: handling preventive actuator maintenance and economics using model predictive control.AIChE Journal,2014,60(6): 2179?2196

15 Lao L F,Ellis M,Christofides P D.Economic model predictive control of transport-reaction processes.Industrial& Engineering Chemistry Research,2014,53(18):7382?7396

17 Rawlings J B,Angeli D,Bates C N.Fundamentals of economic model predictive control.In:Proceedings of the 51st IEEE Conference on Decision and Control.Maui,HI:IEEE, 2012.3851?3861

19 Heidarinejad M,Liu J F,Christofides P D.Economic model predictive control of nonlinear process systems using Lyapunov techniques.AIChE Journal,2012,58(3):855?870

20 Ellis M,Christofides P D.On finite-time and infinite-time cost improvement of economic model predictive control for nonlinear systems.Automatica,2014,50(10):2561?2569

21 Maree J P,Imsland L.On multi-objective economic predictive control of cyclic process operation.Journal of Process Control,2014,24(8):1328?1336

22 Vallerio M,van Impe J,Logist F.Tuning of NMPC controllers via multi-objective optimisation.Computers and Chemical Engineering,2014,61(11):38?50

23 Pan Hong-Guang,Gao Hai-Nan,Sun Yao,Zhang Ying, Ding Bao-Cang.The algorithm and software implementation for double-layered model predictive control based on multi-priority rank steady-state optimization.Acta Automatica Sinica,2014,40(3):405?414 (潘紅光,高海南,孫耀,張英,丁寶蒼.基于多優先級穩態優化的雙層結構預測控制算法及軟件實現.自動化學報,2014,40(3): 405?414)

24 Bemporad A,de la Pea D M.Multiobjective model predictive control.Automatica,2009,45(12):2823?2830

25 Zou Tao,Wang Xi,Li Shao-Yuan.Multi-model predictive control for nonlinear systems based on mixed logic.Acta Automatica Sinica,2007,33(2):188?192 (鄒濤,王昕,李少遠.基于混合邏輯的非線性系統多模型預測控制.自動化學報,2007,33(2):188?192)

26 Wang H Y,Huang D X,Jin Y H.A hybrid model predictive control for handling infeasibility and constraint prioritization.Chinese Journal of Chemical Engineering,2005,13(2): 211?217

27 Tyler M L,Morari M.Propositional logic in control and monitoring problems.Automatica,1999,35(4):565?582

28 He De-Feng,Song Xiu-Lan,Huang Hua.Stabilizing constrained model predictive control with prioritized multiobjectives.Control and Decision,2013,28(12):1831?1836 (何德峰,宋秀蘭,黃驊.優先級多目標穩定化約束模型預測控制.控制與決策,2013,28(12):1831?1836)

29 He D F,Wang L,Sun J.On stability of multiobjective NMPC with objective prioritization.Automatica,2015,57: 189?198

30 Ocampo-Martinez C,Ingimundarson A,Puig V,Quevedo J.Objective prioritization using lexicographic minimizers for MPC of sewer networks.IEEE Transactions on Control Systems Technology,2008,16(1):113?121

31 Zavala V M,Flores-Tlacuahuac A.Stability of multiobjective predictive control:a utopia-tracking approach.Automatica,2012,48(10):2627?2632

32 He D F,Wang L,Yu L.Multi-objective nonlinear predictive control of process systems:a dual-mode tracking control approach.Journal of Process Control,2015,25(3):142?151

34 Yu Shu-You,Chen Hong,Zhang Peng,Li Xue-Jun.An LMI optimization approach for enlarging the terminal region of MPC for nonlinear systems.Acta Automatica Sinica,2008, 34(7):798?804 (于樹友,陳虹,張鵬,李學軍.一種基于LMI的非線性模型預測控制終端域優化方法.自動化學報,2008,34(7):798?804)

35 He D F,Yu L,Song X L.Optimized-based stabilization of constrained nonlinear systems:a receding horizon approach. Asian Journal of Control,2014,16(6):1693?1701

36 Xi Yu-Geng,Li De-Wei.Fundamental philosophy and status of qualitative synthesis of model predictive control.Acta Automatica Sinica,2008,34(10):1225?1234 (席裕庚,李德偉.預測控制定性綜合理論的基本思路和研究現狀.自動化學報,2008,34(10):1225?1234)

37 He De-Feng,Ding Bao-Cang,Yu Shu-You.Review of fundamental properties and topics of model predictive control for nonlinear systems.Control Theory and Applications,2013, 30(3):273?287 (何德峰,丁寶蒼,于樹友.非線性系統模型預測控制若干基本特點與主題回顧.控制理論與應用,2013,30(3):273?287)

38 Mhaskar P,El-Farra N H,Christofides P D.Stabilization of nonlinear systems with state and control constraints using Lyapunov-based predictive control.System&Control Letters,2006,55(8):650?659

39 Xu Jiu-Ping,Li Jun.Multiple Objective Decision Making Theory and Methods.Beijing:Tsinghua University Press, 2005. (徐玖平,李軍.多目標決策的理論與方法.北京:清華大學出版社, 2005.)

何德峰 浙江工業大學信息工程學院教授.2008年獲得中國科學技術大學自動化系博士學位.主要研究方向為魯棒與預測控制.

E-mail:hdfzj@zjut.edu.cn

(HE De-Feng Professor at the College of Information Engineering,Zhejiang University of Technology.He received his Ph.D.degree from the Department of Automation,University of Science and Technology of China in 2008.His research interest covers robust and predictive control.)

Stabilizing Economic Model Predictive Control of Constrained Nonlinear Systems

HE De-Feng1

This paper proposes a novelty economic model predictive control(EMPC)scheme with guaranteed stability for constrained nonlinear systems.Some auxiliary positive-definite functions at economy optimal equilibrium points are introduced for economic performance functions that are generally non-convex and non-positive-definite.The optimal value function of the auxiliary function is used to define an adjustable stability constraint which is imposed on the original EMPC optimization problem.By the triplet of terminal constrained sets,terminal penalty functions and local controllers, it is proved that the closed-loop system is asymptotically stable at the economically optimal equilibrium point and has an asymptotic average performance.Moreover,the proposed EMPC scheme is extended to optimization control of multiple economic performance functions,together with the concept of multi-objective utopia points.Then a stabilizing multiobjective EMPC scheme is presented.Finally,the effectiveness of the obtained results is illustrated by a simulation example of a continuously stirred tank reactor.

Model predictive control(MPC),nonlinear systems,economic optimization,stability,multi-objective control Citation He De-Feng.Stabilizing economic model predictive control of constrained nonlinear systems.Acta Automatica Sinica,2016,42(11):1680?1690

何德峰.約束非線性系統穩定經濟模型預測控制.自動化學報,2016,42(11):1680?1690

2015-04-20 錄用日期2016-06-30

Manuscript received April 20,2015;accepted June 30,2016

國家自然科學基金(61374111),浙江省公益技術應用研究計劃項目(2015C31057)資助

Supported by National Natural Science Foundation of China (61374111),Public Welfare Technology Application Research Project of Zhejiang Province(2015C31057)

本文責任編委喬俊飛

Recommended by Associate Editor QIAO Jun-Fei

1.浙江工業大學信息工程學院杭州310023

1.College of Information Engineering,Zhejiang University of Technology,Hangzhou 310023

DOI 10.16383/j.aas.2016.c150234