隨機地震作用下三維桁架結構拓撲優化
洪 晨 李棟泓
(華南理工大學土木與交通學院,廣東 廣州 510640)
?
隨機地震作用下三維桁架結構拓撲優化
洪 晨 李棟泓
(華南理工大學土木與交通學院,廣東 廣州 510640)
建立了以結構體積最小為目標、指定節點響應方差為約束的優化模型,采用時域顯式法分析了隨機地震作用下結構響應及其靈敏度,并結合全局收斂的移動漸進線法(GCMMA)求解了結構拓撲優化問題,最后通過三維桁架結構數值算例驗證了該拓撲優化的可行性。
拓撲優化,三維桁架結構,時域顯式法,隨機地震作用
0 引言
結構拓撲優化在結構設計中具有良好的實用性,已經成為當今結構優化設計領域中的一個研究熱點。目前,結構拓撲優化研究大多集中在靜力領域,動力學拓撲優化的研究成果相對較少;而在實際工程中,結構不僅承受靜荷載,而且還受到地震、氣流等產生的隨機動力作用的影響。因此,開展隨機荷載作用下的結構拓撲優化研究具有重要的工程應用價值。
近年來,蘇成,徐瑞[1]從時域角度出發,提出了非平穩隨機振動分析的時域顯式法,該方法在大型復雜結構分析過程中表現出良好的計算效率[2]。Z.Q.Hu,C.Su等[3]采用直接微分法求解靈敏度方程,提出了非平穩隨機振動靈敏度分析的時域顯式法。
因此,本文建立以結構隨機響應為約束、結構體積最小為目標的優化模型,并采用上述時域顯式法分析結構隨機響應及其靈敏度,最后結合全局收斂的移動漸近線法(GCMMA)[4]求解結構拓撲優化問題。
1 優化模型的建立及求解
以結構體積最小為優化目標,指定節點位移方差最大值不超過預定限值為約束條件,分別以桿件截面面積及節點坐標為設計變量,則其優化模型可以表達為如下形式:
(1)
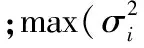
2 結構動力響應及其靈敏度分析
2.1 動力響應分析的時域顯式法
考慮n維自由度的線性結構系統,地震作用下的動力學方程可以表示為:
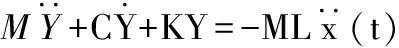
(2)
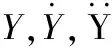
由文獻[1]可得,當系統初始狀態V0為零向量時,第i時刻結構系統狀態Vi在時域內可顯式表達為:
Vi=BiRi
(3)
其中,
(4)

在分析過程中,通常并不需要求解所有響應向量,從而第i時刻結構某自由度的響應方差可表示為:
cov(vi,vi)=φBicov(Ri,Ri)(φBi)T
(5)
其中,φ為某自由度響應的定位向量,其元素由0和1組成。
2.2 動力響應靈敏度分析的時域顯式法
基于以上動力響應時域顯式表達的基本思路,同理可得動力響應靈敏度的時域顯式表達。設θ代表線性結構的某設計變量,動力學方程式兩端對θ求偏導,且假設地震加速度與設計變量無關,整理可得:
(6)
對比上式發現,兩式僅荷載項不同,因此,當系統初始狀態靈敏度?V0/?θ為零向量時,由文獻[3]可得第i時刻結構響應靈敏度的時域顯式表達為:
(7)
其中,
(8)
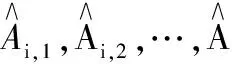
(9)
將公式整理可得第i時刻結構某自由度響應方差靈敏度的計算表達式:
(10)
3 數值算例
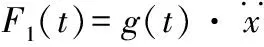
g(t)=δ(e-β1t-eβ2t)
(11)
(12)
其中,ωg為地基土卓越頻率,取14 rad/s;ζg為地基土阻尼比,取0.6;S0為地面水平運動加速度的譜強度因子,均取0.05 m2/s3,Δt為計算時間步長,取0.05 s。
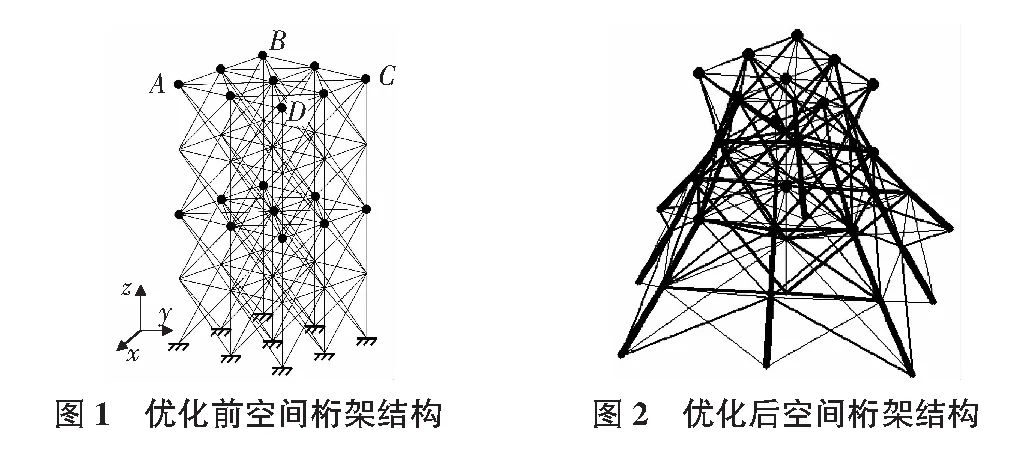
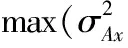

表1 優化前后結構的位移方差及總體積

參數σ2Axmax/m2σ2Aymax/m2總體積/m3優化前6.06×10-106.06×10-10242.4優化后4.91×10-114.91×10-11164.3
4 結語
本文建立以結構隨機響應為約束、結構體積最小為目標的優化模型,采用時域顯式法求解結構隨機響應及其靈敏度,并結合全局收斂的移動漸近線法(GCMMA)求解優化問題,通過數值算例驗證該方法可以很好的推廣到空間桁架結構的隨機動力拓撲優化問題中。從上述的圖表中可得,空間桁架結構在滿足位移方差約束的條件下,結構材料總用量得到了節省,優化后的結構拓撲布局較為合理,對工程結構的優化設計具有一定的指導意義。
[1] 蘇 成,徐 瑞.非平穩隨機激勵下結構隨機振動時域分析法[J].工程力學,2010,27(12):77-83.
[2] 蘇 成,徐 瑞,劉小璐,等.大跨度空間結構抗震分析的非平穩隨機振動時域顯式法[J].建筑結構學報,2011,32(11):169-176.
[3] Z.Q.Hu,C.Su,T.C.Chen,et al.An explicit time-domain approach for sensitivity analysis of non-stationary random vibration problems[J].Journal of Sound and Vibration,2016(382):122-139.
[4] K.Svanberg.A class of globally convergent optimization methods based on conservative convex separable approximations[J].SIAM J.Optim,2002(12):555-573.
[5] Cacciola P,Colajanni P,Muscolino G.A modal approach for the evaluation of the response sensitivity of structural systems subjected to non-stationary random Processes[J].Computer Methods in Applied Mechanics and Engineering,2005(194):4344-4361.
Topology optimization of 3D truss structures under random seismic excitations
Hong Chen Li Donghong
(SchoolofCivilEngineeringandTransportation,SouthChinaUniversityofTechnology,Guangzhou510640,China)
The optimization model of 3D truss structures is formulated by taking volume minimization with displacement constraints. Then, the time-domain explicit method is applied to solve the stochastic response and the sensitivity with respect to the design parameters, and combined with the Global Converged Method of Moving Asymptotes(GCMMA) to solve the topology optimization problem. Finally, the numerical example illustrates the computational efficiency of the proposed topology optimization.
topology optimization, 3D truss structures, time-domain explicit method, random seismic excitations
1009-6825(2016)30-0055-02
2016-08-16
洪 晨(1991- ),男,在讀碩士; 李棟泓(1990- ),男,在讀碩士
TU311
A

