灰度變換下圖像Harris角點特征點匹配算法性能分析

盧達龍，翁秀玲，吳 煒，王云峰

(廈門大學 信息科學與技術學院，福建 廈門 361005)

灰度變換下圖像Harris角點特征點匹配算法性能分析

盧達龍，翁秀玲，吳 煒，王云峰

(廈門大學 信息科學與技術學院，福建 廈門 361005)

由于Harris角點理論上具有不隨光照條件改變而改變及旋轉不變性等優點，被廣泛應用于計算機視覺系統中。但實際應用中拍照光線的變化往往會引起圖像的灰度失真，本文對Harris角點提取和SAD、SSD、NCC三種匹配算法在灰度變換下的性能進行了分析。分析結果表明，Harris角點提取具有較好的光照條件魯棒性；而NCC是三種匹配算中灰度變換影響最小的。

圖像匹配；特征點；角點；灰度變換

本文著錄格式：盧達龍，翁秀玲，吳煒，等. 灰度變換下圖像Harris角點特征點匹配算法性能分析[J]. 軟件，2016，37（11）：19-22

0 引言

圖像匹配就是把具有同一場景的兩幅或多幅圖像在空間上對準，進而確定它們之間變換關系的過程，是三維重建的關鍵技術，是計算機視覺的核心問題?，F有的匹配算法[1]分為基于灰度相關的匹配算法、基于相位相關的匹配算法及基于特征相關的匹配算法。所謂特征點指的是滿足一定特征條件的特征區域的位置，能夠反映圖像的某種穩定結構，可以體現圖像的本質特性。由于特征點只占圖像像素的小部分，所以基于特征的圖像匹配算法大大減小了參與匹配的信息量，容易實現圖像的實時匹配，是目前計算機視覺的研究熱點之一。

已有提取圖像特征點的算法很多，包括Moravec算法、Forstner算法、SURF算法、SIFT算法、Harris角點算法等。在各種各樣的圖像特征點中，Harris角點理論上具有不隨光照條件改變而改變及旋轉不變性等優點[2]，利于圖像的可靠匹配。Harris角點在目標識別、目標跟蹤、運動估計、三維場景重構、圖像配準等計算機視覺領域有著非常重要的作用。

實際應用中拍照光線的變化往往會引起圖像的灰度失真[3]，因此光照魯棒性也是衡量一個特征點匹配過程的指標之一。本文將在當前計算機視覺研究領域應用最廣的圖像集上進行基于Harris角點的絕對誤差和測度SAD（Sum of absolute differences）、

不相似測度SSD（Sum of square differences）、相似測度NCC（Normalized Cross Correlation）等匹配算法在灰度變換下的性能分析。

1 Harris角點提取算法

Harris角點[4-7]檢測法是一種基于圖像灰度的檢測方法，是由Harris和Stephens提出的，主要是通過計算每個像素鄰域的灰度變化矩陣來檢測角點，定義矩陣C為：

式中，xI為x方向的梯度，yI為y方向的梯度。設α、β為矩陣C的特征值，當α、β都很小時，檢測到的點是平坦區域點；當α、β之間只有一個較大而另一個較小時，檢測到的點為邊緣點；當α、β都較大時，提示沿著任意方向移動，圖像的灰度都將導致明顯的變化，表示檢測到的點是角點。

為了便于提取Harris角點，根據式（2）與式（3）所示矩陣C的行列式()DetC與跡()TrC定義Harris角點的響應函數M如式（4）所示。

式（4）中k值Harris推薦為0.04。當M值大于一定的閾值，并且在周圍8個方向上取到局部極大值時，才判定該點是角點。閾值一般取決于圖像的清晰度以及角點強弱等因素，當圖像較清晰、角點特征較強時，閾值一般取大一些；當圖像較模糊、角點特征較弱時，閾值一般取小一些。

2 灰度變化下特征點匹配算法分析

2.1 基于Harris角點的匹配算法

由于Harris角點提取算法簡單易行，提取特征點穩定，因此很多基于Harris角點的匹配算法被提出。其中，SAD匹配算法、SSD匹配算法、NCC匹配算法是應為最為廣泛的三種。SAD、SSD、NCC算法簡單、速度快，能夠滿足低標準應用的需求，但是算法包含的約束條件不全面(如缺少色彩約束、視覺梯度約束等)，匹配結果噪聲大，對閉塞區域、視差不連續區域和低紋理區域不能兼顧，無法達到高匹配準確率。目前，三種算法通常被用作初始匹配代價函數，很多優秀算法是在此基礎上增加約束條件實現改進與完善。

SAD匹配算法計算參考窗口和目標窗口范圍內所有像素的灰度絕對差的總和，對于以待匹配點為中心的參考窗口，所有目標窗口中唯有以匹配點為中心的目標窗口具有SAD的最小值，SAD值越小表示相似性越高。

設匹配圖的待匹配特點為P（x,y），以此點為中心，取邊長分別2m+1、2n+1的矩形參考窗口；設目標圖中某任一特征點為P′（x′,y′），以此點為中心，取邊長分別2m1+、2n1+的矩形目標窗口，則二者灰度絕對差的總和表達形式如式（5）所示：

圖對應點處的灰度值。如果P（x,y）與P′（x′,y′）為一對匹配點，根據光一致性原理，其SAD值應比較小，并且小于一個判斷閾值。故SAD匹配過程即為選定一個待匹配點后，遍歷目標圖中所有特征點，計算SAD值；如果最小SSD值小于判斷閾值，則最小SAD值對應的目標點即為匹配點。

SSD與SAD類似，是將求灰度差的和改成求灰度差平方的和。即P（x,y）與P′（x′,y′）的SSD值如式（6）所示：

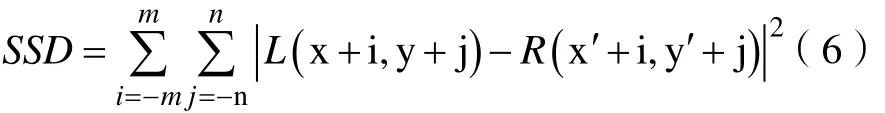
同樣遍歷目標圖中所有特征點，計算SSD值，如最小SSD值小于判斷閾值，則最小SSD值對應的目標點即為匹配點。

歸一化互相關NCC技術是一種相對來說抗噪聲能力強、匹配準確的匹配算法。圖像匹配實際上是比較兩幅圖像的相似性。把圖像展開為向量，就可以歸結為比較兩個向量的相似性。根據向量點乘的定義

式中θ為兩個向量的夾角，若相似，則它們的方向相同，其夾角為0，因此，可以根據cosθ的值來判斷兩個向量的相似性。把其推廣到以待匹配點P（x,y）為中心的參考窗口與以目標點P′（x′,y′）為中心的目標窗口中，則NCC可表示為：

2.2 灰度變化對角點提取的影響分析

在計算機視覺系統中，由于自然環境的影響，連續的兩種圖片可能是在不同的光照條件下拍攝的。由于光照條件可能會引起圖像灰度失真，因此本文首先對Harris角點提取算法在灰度變換下的性能進行分析。

分析基于特征點重復率標準[8]。特征點重復率定于如式（9）所示：

論文首先提取圖1所示計算機視覺領域使用最廣的四幅圖像的Harris角點特征點。

圖1 標準原始圖像

圖2 灰度亮度變換對Harris角點提取的影響

圖3 灰度對比度變換對Harris角點提取的影響

然后分別對圖1進行灰度亮度變換和灰度對比度變換，對變換后的圖像進行Harris角點特征點提取，并計算其與原圖像的重復率?；叶攘炼茸儞Q對重復率的影響曲線如圖2所示；灰度對比度變換對重復率的影響如圖3所示。

綜上，在圖像進行灰度變換后，Harris算法仍然能檢測出大部分原圖上的角點。特別是灰度的亮度變換在很大范圍內對Harris角點提取基本上沒有影響?；叶葘Ρ榷茸兓瘜arris角點提取的影響較大，gamma偏離1越遠，重復率越低。由于光照條件主要會引起灰度的亮度變換，因此，Harris角點提取具有較好的光照條件魯棒性。在光照條件變化比較大的應用場景，應該選取較小閾值進行Harris角點提取，以至于計算機視覺連續拍攝的序列圖片

中可以提取出足夠多的匹配角點，進行圖片配準。

2.3 灰度變化對匹配算法的影響分析

對圖1所示四幅圖像進行灰度亮度變換，然后進行原圖與變換后圖像基于Harris角點的SAD匹配、SSD匹配、NCC匹配，正確匹配率曲線如圖4所示。所謂正確匹配率曲線指的是得到的匹配數占原圖角點比例。試驗結果顯示灰度亮度變換在很大范圍對NCC算法沒有影響。

圖4 灰度亮度變換對匹配的影響

對圖1所示四副圖像進行灰度對比度變換，然后進行原圖與變換后圖像基于Harris角點的SAD匹配、SSD匹配、NCC匹配，正確匹配率曲線如圖5所示。由于灰度對比度對Harris角點提取影響比較大，故正確匹配率比較小。但將圖5與圖3對比，可以看出灰度對比度變換下，NCC的正確匹配率曲線與角點重復率曲線接近，因此可認為灰度對比度對NCC匹配幾乎沒有影響。綜合灰度亮度變換下的匹配結果，可以得出灰度變換對NCC的影響最小，進而NCC具有較好的光照條件魯棒性。

3 結束語

本文進行了Harris角點提取和SAD、SSD、NCC三種匹配算法在灰度變換下的性能進行了分析。試驗結果表明，灰度的亮度變換在很大范圍內對Harris角點提取基本上沒有影響，而灰度對比度變化對Harris角點提取的影響較大，gamma偏離1越遠，重復率越低。由于光照條件主要會引起灰度的亮度變換，因此，Harris角點提取具有較好的光照條件魯棒性；在光照條件變化比較大的應用場景，應該選取較小閾值進行Harris角點提取，以至于計算機視覺連續拍攝的序列圖片中可以提取出足夠多的匹配角點，進行圖片配準。對于匹配算法而言，NCC匹配算法對灰度變換最不敏感，具有一定的光照魯棒性。

圖5 灰度對比度變換對匹配的影響

[1] 謝萍, 鄒崢嶸, 肖奇. 基于Harris角點和SIFT特征的近景影像匹配[J]. 測繪科學, 2012, 37(4): 107-110.

[2] 張勇, 余建平, 孫軍偉, 金鐵. 基于Harris角點匹配算法研究[J]. 計算機與現代化, 2011, 195: 78-81.

[3] 王紅梅, 張科, 李言俊. 圖像匹配研究進展[J]. 計算機工程與應用, 2004, 19: 42-44.

[4] 鐘濤, 張建國, 左俊彥. 基于Harris角點檢測的圖像配準新算法[J]. 醫學影像工程學, 2016, 10:785-789.

[5] 陳夢婷, 閆冬梅, 王剛. 基于Harris 角點和SIFT 描述符的高分辨率遙感影像匹配算法[J]. 中國圖象圖形學報, 2012, 17(11): 1453-1459.

[6] 龔平, 劉相濱, 周鵬. 一種改進的Harris角點檢測算法[J].計算機工程與應用, 2010, 46(11): 173-175.

[7] Bellavia F, Tegolo D, Valenti C,Improving harris corner selection strategy[J]. IEEE Xplore, 2011, 5(2): 87-96.

[8] 張春美, 龔志輝, 黃艷. 幾種特征點提取算法的性能評估及改進[J]. 測繪科學技術學報, 2008, 25(3): 231-234.

Performance Evaluation of Image Feature Point Matching Based on Harris Corner

LU Da-long, WENG Xiu-ling, WU Wei, WANG Yun-feng
(School of information science and engineering, Xiamen University, Xiamen Fujian 361005, China)

When the images are taken with the variance in light rays and the angle transformation, The Harris corners of these images are not change. So The Harris corners are extensively applied in Computer vision system. However, the gray of images is usually not true if the images are photoed with the variance in light rays. The performance of Harris corner, SAD, SSD and NCC is evaluated. The evaluation result shows that the Harris corners are robust to variance in light rays and the NCC is least affected by gray transformation.

Image matching; Feature points; Corner; Gray transformation

TP391

A

10.3969/j.issn.1003-6970.2016.11.005

國家自然科學基金資助項目(61274133)

盧達龍(1991-)，男，碩士，主要研究方向：數字集成電路設計及SLAM系統軟硬件設計。

王云峰，博士，副教授，主要研究方向：數字集成電路設計及SLAM系統軟硬件設計。