輕質物體模型特性在高考解題中的應用
王高生
(淮南市第二中學 安徽 淮南 232000)
?
輕質物體模型特性在高考解題中的應用
王高生
(淮南市第二中學 安徽 淮南 232000)
由于輕質物體自身沒有質量,所以根據牛頓第二定律:F合=ma,由于m=0,故F合=0.即:輕質物體在任何情況下所受的合力必須為零.而其加速度a可以為任意值,在極短的時間內,其速度變化可以無窮大,故其速度可以突變.
高中物理 輕質物體 牛頓第二定律 速度突變
高中物理中有很多理想化的模型,其中輕質物體是最常見也是應用最多的一種模型,很多同學都知道所謂輕質物體就是物體的質量忽略不計,但是對其受力和運動特性卻沒有研究和重視,而其受力及運動特性往往在高考解題中充當了突破口的作用,充分認識了輕質物體的力學性質,往往可以取得意想不到的效果.
(1)輕質物體的受力特征
根據牛頓第二定律:F合=ma,當物體的質量m=0時,F合=0.即:輕質物體在任何情況下所受的合力必須為零.即使其隨其他物體一起加速減速的時候其所受合力還是為零.
(2)輕質物體的運動特性
由于輕質物體自身沒有質量,所以根據牛頓第二定律:F合=ma,其加速度a可以為任意值,在一個瞬間其速度就可以突變.實際解題中,其往往都是與其他物體接觸,即其與其他物體一起運動,故其運動狀態往往與其一起運動的物體相同,根據其他物體的運動需求而變化.
為了更好地說明輕質物體模型的力學特征在解題中充當突破口的作用,我們選取兩道在高考中得分率較低的兩道典型題來加以說明.
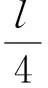
(1)若彈簧的勁度系數為κ,求輕桿開始移動時,彈簧的壓縮量x;
(2)求為使裝置安全工作,允許該小車撞擊的最大速度vmax;

圖1
分析:本題是一道關于彈簧能量問題的一個典型例題,問題的關鍵在于分析清楚彈簧的初末狀態,第一次小車接觸彈簧前,彈簧處于原長,而小車接觸彈簧后壓縮彈簧,當彈簧的彈力達到了輕桿的最大摩擦力f時,輕桿開始運動,之后彈簧的形變量會不會改變?
如果對于輕質物體的受力及運動特性沒有清楚的認識,就極有可能認為:此時小車的速度大于輕桿的速度,彈簧還會繼續發生一定的形變,直到兩物體小車與輕桿速度相同.這樣這道題就陷入了誤區,也就不可能正確的求解了.
其實根據輕質物體的受力特性:F合=0,可知:彈簧的彈力必須始終等于輕桿所受的摩擦力,即:F彈=f,彈簧彈力不變形變量不變.至于輕桿比小車速度慢的問題,由于輕桿作為輕質物體,根據輕質物體運動特性,速度可以突變成與小車的速度相等,所以小車與輕桿間距離可以保持不變進一步支持了彈簧的彈力不變形變量不變的結論.
同樣的道理,第二次小車以最大速度接近彈簧,彈簧的初末狀態與第一次完全相同.故:有兩次小車接近過程中彈簧的初末狀態相同,彈簧彈力做功完全相同.
解:(1)由于輕桿所受彈力等于摩擦力,且當摩擦力等于其最大靜摩擦力時桿才會動.故

(2)第一次接近,由動能定理可知

同理小車第二次接近過程中可列
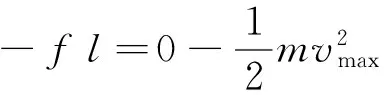
聯立可得
【例2】(2011年高考江蘇卷第9題)如圖2所示,傾角為θ的等腰三角形斜面固定在水平面上,一足夠長的輕質綢帶跨過斜面的頂端鋪放在斜面的兩側,綢帶與斜面間無摩擦.現將質量分別為M,m(M>m)的小物塊同時輕放在斜面兩側的綢帶上.兩物塊與綢帶間的動摩擦因數相等,且最大靜摩擦力與滑動摩擦力大小相等.在θ角取不同值的情況下,下列說法正確的有
A.兩物塊所受摩擦力的大小總是相等
B.兩物塊不可能同時相對綢帶靜止
C.M不可能相對綢帶發生滑動
D.m不可能相對斜面向上滑動

圖2
解析:很多學生而言這道題無從下手,原因是兩個物體,相互制約,很難找到突破口,而如果我們抓住綢帶這一輕質物體的受力與運動特征,就可以迎刃而解.
首先從受力角度分析:由于綢帶是輕質物體,所以所受合力必須為零,因此m與M所受的摩擦力必須等大且相互抵消.故選項A正確.
如果m與M都與綢帶出現相對靜止,則都是靜摩擦力且大小相等,而M與m由于下滑分力不相等,故不可能同時靜止,應該是M與m一起運動,由于M下滑力大,故M向下加速,m向上加速,即
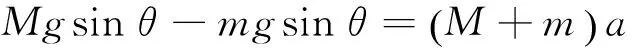
且f靜-mgsin θ=ma 滿足兩個條件的靜摩擦力即可.故可能出現這種情況,所以選項B錯誤.
假設如果M出現相對滑動,綢帶受到的其摩擦力為μMgcos θ,此時無論m與絲綢相對靜止,其與綢帶間為靜摩擦,由于
f靜≤μmgcos θ<μMgcos θ
故兩個物體給綢帶的摩擦力不可能相等,綢帶所受合力不為零,不符合輕質物體特征.所以假設不成立,即M與綢帶不可能出現相對滑動.得出選項C正確.
在選項B中我們已經證明m與M相對絲綢靜止時,m應向上運動.所以選項D錯誤.
小結:可見,如果把握住了輕質物體的受力及運動特性,可以幫助我們分析其他物體的運動和受力特征,助推解題思路的形成,有利于防止學生在解決常規問題時形成的思維定勢,突破學生思維障礙,從而快速做出正確判斷,事半功倍.
1 于春梅,李東方.輕質物體的受力特點.中學物理高中版,2000
2015-12-08)

