挖掘機(jī)動(dòng)力總成懸置系統(tǒng)隔振分析及優(yōu)化

邢樹(shù)鑫,俞松松,李 武

(廣西柳工機(jī)械股份有限公司 廣西柳州 545007)

?

挖掘機(jī)動(dòng)力總成懸置系統(tǒng)隔振分析及優(yōu)化

邢樹(shù)鑫,俞松松,李 武

(廣西柳工機(jī)械股份有限公司 廣西柳州 545007)

針對(duì)某型挖掘機(jī)怠速工況下出現(xiàn)動(dòng)力總成晃動(dòng)較大的現(xiàn)象,建立了動(dòng)力總成懸置系統(tǒng)動(dòng)力學(xué)模型.運(yùn)用能量解耦方法,以懸置系統(tǒng)的動(dòng)剛度為設(shè)計(jì)變量,以懸置系統(tǒng)的模態(tài)頻率為約束條件,以主要激勵(lì)方向的解耦率為優(yōu)化目標(biāo),對(duì)動(dòng)力總成懸置系統(tǒng)進(jìn)行了優(yōu)化.優(yōu)化后系統(tǒng)的關(guān)鍵方向解耦率最大提高了20.2%.分別對(duì)優(yōu)化前后的懸置系統(tǒng)進(jìn)行了振動(dòng)測(cè)試,結(jié)果顯示優(yōu)化后懸置系統(tǒng)的隔振性能有了明顯提高.

動(dòng)力總成懸置系統(tǒng); 振動(dòng); 能量解耦; MATLAB

XING Shu-xin,YU Song-song,LI Wu

(Guangxi Liugong Machinery Co.,Ltd.,Liuzhou 545007,China)

挖掘機(jī)動(dòng)力總成通過(guò)懸置系統(tǒng)與回轉(zhuǎn)平臺(tái)連接,懸置系統(tǒng)性能設(shè)計(jì)的好壞直接影響到動(dòng)力總成振動(dòng)向整機(jī)的傳遞,進(jìn)而影響整機(jī)的操作舒適性.本文針對(duì)某型挖掘機(jī)在測(cè)試過(guò)程中出現(xiàn)怠速工況下振動(dòng)較大這一問(wèn)題,建立了挖掘機(jī)動(dòng)力總成懸置系統(tǒng)的動(dòng)力學(xué)模型,以懸置系統(tǒng)動(dòng)剛度為設(shè)計(jì)變量,以主要激勵(lì)方向的解耦率為優(yōu)化目標(biāo),采用二次規(guī)劃法對(duì)懸置系統(tǒng)的動(dòng)剛度進(jìn)行優(yōu)化,從而改善了該挖掘機(jī)怠速工況下動(dòng)力總成懸置系統(tǒng)的隔振性能.最后,通過(guò)試驗(yàn)驗(yàn)證了優(yōu)化設(shè)計(jì)結(jié)果的正確性.

1 懸置系統(tǒng)的能量解耦法

挖掘機(jī)動(dòng)力總成懸置系統(tǒng)主要由風(fēng)扇、發(fā)動(dòng)機(jī)、減震器、消音器和液壓泵等部件組成,動(dòng)力總成懸置系統(tǒng)如圖1所示.在進(jìn)行動(dòng)力總成懸置系統(tǒng)建模時(shí),一般假定回轉(zhuǎn)平臺(tái)是剛性的,并將動(dòng)力總成懸置系統(tǒng)簡(jiǎn)化為空間六自由度振動(dòng)系統(tǒng).

圖1中坐標(biāo)系為動(dòng)力總成質(zhì)心坐標(biāo)系,動(dòng)力總成質(zhì)心為坐標(biāo)系的原點(diǎn)O,x軸平行于發(fā)動(dòng)機(jī)曲軸并指向風(fēng)扇側(cè),z軸垂直向上,y軸按右手法則確定.由于減震器的阻尼不大,并且其主要作用是降低共振峰值,因此在分析系統(tǒng)自由振動(dòng)時(shí)忽略阻尼,則系統(tǒng)的振動(dòng)微分方程為

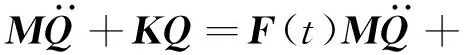
zKQ=F(t)

(1)

式中:M為系統(tǒng)的質(zhì)量矩陣;K為系統(tǒng)的剛度

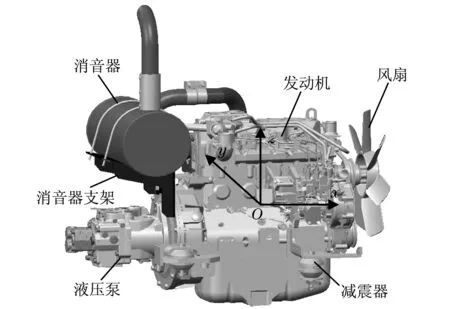
圖1 動(dòng)力總成懸置系統(tǒng)模型

矩陣;Q為廣義坐標(biāo)列向量;F(t)為系統(tǒng)所受的激振力.

對(duì)于固有頻率的求解一般采用矩陣迭代法,但是通常動(dòng)力總成懸置系統(tǒng)的6個(gè)自由度的振動(dòng)是耦合的,沿懸置系統(tǒng)廣義坐標(biāo)的任意一個(gè)激勵(lì)都將激起系統(tǒng)的多個(gè)模態(tài),導(dǎo)致發(fā)動(dòng)機(jī)的振幅加大,由于懸置系統(tǒng)經(jīng)常存在某些振動(dòng)模態(tài)的耦合,導(dǎo)致隔振效果的下降.因此,在設(shè)計(jì)懸置系統(tǒng)時(shí),應(yīng)盡量使其具有較高的振動(dòng)解耦程度,通常采用能量解耦法[1-2],其計(jì)算方法如下:

根據(jù)式(1)可以求出動(dòng)力總成在各階主振動(dòng)時(shí)的能量分布,將它寫(xiě)成矩陣形式,并定義為能量分布矩陣.當(dāng)動(dòng)力總成以第j階固有頻率振動(dòng)時(shí),此矩陣的第k行l(wèi)列元素為

(2)

式中:φj為Φ的第j個(gè)列向量,即系統(tǒng)的第j階主振型;(φj)k及(φj)l分別為φj的第k 及第l個(gè)元素;mkl為系統(tǒng)質(zhì)量矩陣的第k行l(wèi)列元素;ωj為系統(tǒng)的第j階固有頻率;k,l,j =1,2,…,6.當(dāng)系統(tǒng)以第j階固有頻率振動(dòng)時(shí),第k個(gè)廣義坐標(biāo)所占的能量百分比為

×100%

(3)

式中:Pkj為系統(tǒng)在作第j階固有頻率振動(dòng)時(shí),振動(dòng)占優(yōu)方向所占的振動(dòng)能量百分比,此值越大系統(tǒng)的解耦程度越高.

2 懸置系統(tǒng)優(yōu)化設(shè)計(jì)

2.1 激勵(lì)頻率

該動(dòng)力總成采用四缸、四沖程柴油機(jī),其工作轉(zhuǎn)速范圍為900～2 100 r·min-1,則發(fā)動(dòng)機(jī)的激勵(lì)頻率為

fi=n i /60

式中fi為發(fā)動(dòng)機(jī)的激勵(lì)頻率;n為發(fā)動(dòng)機(jī)轉(zhuǎn)速;i為激勵(lì)頻率的階次,i=1,2,3,…….對(duì)于四缸四沖程發(fā)動(dòng)機(jī),其主要激勵(lì)為二階不平衡慣性力[3],則對(duì)應(yīng)的激勵(lì)頻率范圍為30～70 Hz.因此,要想避免共振,動(dòng)力總成懸置系統(tǒng)的固有頻率就不能落在這個(gè)頻率范圍內(nèi).

2.2 解耦分析

動(dòng)力總成質(zhì)量為339.4 kg,共布置有4個(gè)橡膠懸置點(diǎn),各懸置點(diǎn)平置布置,布置方式如圖1所示,動(dòng)力總成懸置系統(tǒng)各項(xiàng)參數(shù)如表1～3所示.

表1 優(yōu)化前懸置系統(tǒng)各向動(dòng)剛度

表2 懸置系統(tǒng)位置參數(shù)

表3 動(dòng)力總成慣性張量(單位：kg·m2)

根據(jù)能量解耦理論,應(yīng)用MATLAB軟件編制程序?qū)υ摍C(jī)動(dòng)力總成懸置系統(tǒng)進(jìn)行性能分析.將上表1～3中的各項(xiàng)參數(shù)代入程序進(jìn)行計(jì)算,可得系統(tǒng)固有特性,如表4所示.

由表4可以看出,該動(dòng)力總成懸置系統(tǒng)的減振性能有以下特點(diǎn):

(1) 懸置系統(tǒng)的模態(tài)頻率范圍為11.48～28.66 Hz,同發(fā)動(dòng)機(jī)的激勵(lì)頻率極為接近,在怠速情況下無(wú)法保證減振性能,易發(fā)生共振.樣機(jī)在怠速時(shí)的共振現(xiàn)象也驗(yàn)證了該結(jié)論的正確性.

(2) 從解耦率來(lái)看,除第3,5階模態(tài)能量解耦程度較高之外,其他各階模態(tài)能量解耦程度均較低,易引發(fā)模態(tài)振動(dòng)耦合,從而削弱減振性能.

2.3 優(yōu)化設(shè)計(jì)

由于四缸機(jī)的2階慣性力和轉(zhuǎn)矩是懸置系統(tǒng)的主要激振力,所以?xún)?yōu)化分析時(shí),主要考慮增大沿z方向和繞x軸的能量解耦情況.對(duì)應(yīng)于能量分布矩陣,即要使P33,P44達(dá)到最大值,寫(xiě)成目標(biāo)函數(shù)形式為

(4)

表4 原動(dòng)力總成懸置系統(tǒng)的固有頻率和能量分布

要提高懸置系統(tǒng)某個(gè)方向上的解耦程度,可以通過(guò)改變懸置的位置、傾角以及剛度等方法來(lái)達(dá)到.但是由于受到整機(jī)空間的限制,懸置位置和支撐角度難以改變.因此,懸置系統(tǒng)的設(shè)計(jì)變量選擇為:左右減震器z方向的拉壓剛度和x，y方向的剪切剛度.在設(shè)計(jì)變量的范圍選擇方面,綜合考慮動(dòng)反力和動(dòng)力總成懸置系統(tǒng)位移兩個(gè)因素[4],取剛度系數(shù)上、下限為300～1 300 N·mm-1.同時(shí),針對(duì)該動(dòng)力總成懸置系統(tǒng)在怠速時(shí)的共振現(xiàn)象對(duì)于該系統(tǒng)的模態(tài)頻率也應(yīng)進(jìn)行限制.根據(jù)發(fā)動(dòng)機(jī)相關(guān)參數(shù)以及隔振理論[5]系統(tǒng)的固有頻率范圍應(yīng)設(shè)為5～22 Hz.

由于目標(biāo)函數(shù)和約束條件都是含有自變量的非線性函數(shù),因此使用序列二次規(guī)劃法編制程序進(jìn)行優(yōu)化求解.優(yōu)化后各懸置剛度如表5所示.

表5 優(yōu)化后懸置系統(tǒng)各向動(dòng)剛度

應(yīng)用優(yōu)化后的減震器參數(shù)進(jìn)行能量分布計(jì)算,結(jié)果如表6所示,從中可以看出:

(1) 優(yōu)化后動(dòng)力總成懸置系統(tǒng)的模態(tài)頻率范圍為9.09～21.65 Hz,較優(yōu)化前降低24.5%,有效避開(kāi)了發(fā)動(dòng)機(jī)的激勵(lì)頻率.

(2) 對(duì)比分析表4與表6可以發(fā)現(xiàn),除繞z軸方向以外,該懸置系統(tǒng)模態(tài)能量解耦狀況總體上獲得了一定程度的提高,尤其是繞x軸方向的解耦提高程度最大,由優(yōu)化前的72.57%提高到87.2%,提高幅度達(dá)20.2%.

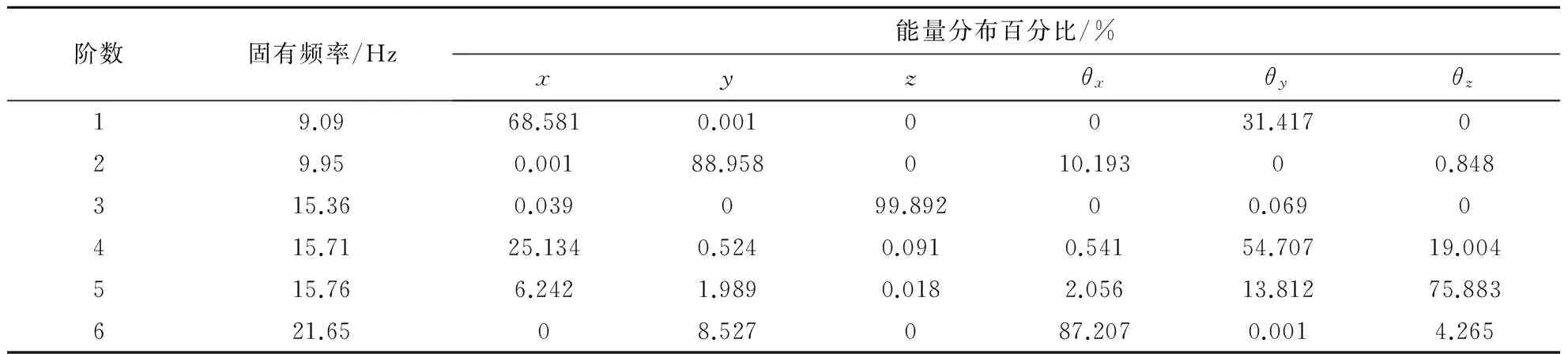
表6 優(yōu)化后動(dòng)力總成懸置系統(tǒng)的固有頻率和能量分布

3 試驗(yàn)驗(yàn)證

3.1 懸置系統(tǒng)振動(dòng)測(cè)試

為驗(yàn)證懸置系統(tǒng)的優(yōu)化計(jì)算結(jié)果,分別對(duì)優(yōu)化前后的動(dòng)力總成懸置系統(tǒng)進(jìn)行振動(dòng)測(cè)試.在4個(gè)動(dòng)力總成減震器支座上各布置一個(gè)3向加速度傳感器,4個(gè)回轉(zhuǎn)平臺(tái)減震器支座上各布置一個(gè)3向加速度傳感器,共計(jì)8個(gè)加速度傳感器.振動(dòng)傳感器采用美國(guó)PCB公司的三軸向加速度傳感器,數(shù)據(jù)采集使用LMS動(dòng)態(tài)數(shù)據(jù)采集儀,測(cè)試由發(fā)動(dòng)機(jī)最低轉(zhuǎn)速開(kāi)始,逐步升高至最高轉(zhuǎn)速,中間分別對(duì)多個(gè)檔位進(jìn)行對(duì)比.

3.2 結(jié)果分析

振動(dòng)傳遞率[6]是衡量懸置系統(tǒng)匹配效果的重要指標(biāo),一般用分貝的形式表達(dá)為

(5)

式中:ad為發(fā)動(dòng)機(jī)的振動(dòng)加速度;aj為回轉(zhuǎn)平臺(tái)的振動(dòng)加速度,一般要求傳遞率高于20 dB.分析過(guò)程中,使用LMS Test.Lab數(shù)據(jù)處理軟件對(duì)測(cè)試數(shù)據(jù)進(jìn)行處理,得到各測(cè)試點(diǎn)的振動(dòng)加速度均方根值.各懸置點(diǎn)的振動(dòng)傳遞率如圖2所示.

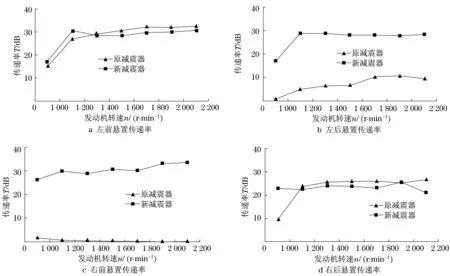
圖2 優(yōu)化前后各懸置點(diǎn)Z向傳遞率

Fig.2 Transmissibility of mounts on Z direction before and after optimization

由圖2可以看出,改進(jìn)前左后、右前懸置點(diǎn)的傳遞率較低分別為10,0 dB,沒(méi)有起到較好的隔振作用.改進(jìn)后除怠速情況,各懸置點(diǎn)的傳遞率均在30 dB左右,起到了較好的隔振作用.怠速情況下未出現(xiàn)動(dòng)力總成共振現(xiàn)象,改進(jìn)有效.

4 總結(jié)

本文結(jié)合多自由度系統(tǒng)振動(dòng)解耦和固有頻率匹配理論,開(kāi)發(fā)了用于挖掘機(jī)動(dòng)力總成懸置系統(tǒng)性能分析和優(yōu)化設(shè)計(jì)的程序.對(duì)某型挖掘機(jī)的動(dòng)力總成懸置系統(tǒng)進(jìn)行了減振性能分析和優(yōu)化設(shè)計(jì).經(jīng)試驗(yàn)驗(yàn)證,優(yōu)化后懸置系統(tǒng)怠速工況下的傳遞率大幅提高,解決了該挖掘機(jī)動(dòng)力總成怠速時(shí)的共振問(wèn)題.

[1] 李立波.發(fā)動(dòng)機(jī)懸置優(yōu)化計(jì)算 [J].合肥工業(yè)大學(xué)學(xué)報(bào),2007,30(12):86-89.

LI Libo.Engine suspenion optimization[J].Journal of Hefei University of Technology,2007,30(12):86-89.

[2] 趙彤航.CA1261汽車(chē)發(fā)動(dòng)機(jī)懸置系統(tǒng)隔振的研究[D].長(zhǎng)春:吉林大學(xué),2002.

ZHAO Tonghang.Study on vibration isolation of engine mounting system of CA1261 vehicle[D].Changchun:Jilin University,2002.

[3] 陳劍,徐陳夏.發(fā)動(dòng)機(jī)懸置系統(tǒng)優(yōu)化設(shè)計(jì)及其可靠性分析[J].汽車(chē)工程,2009,31 (3):234-238

CHEN Jian,XU Chenxia.Optimization design and reliability analysis of engine mount system[J].Automotive Engineering,2009,31 (3):234-238.

[4] 莊偉超,王良模,殷召平,等.基于遺傳算法的混合動(dòng)力汽車(chē)動(dòng)力總成懸置系統(tǒng)的優(yōu)化設(shè)計(jì)研究 [J].振動(dòng)與沖擊,2015,34(8):209-213.

ZHUANG Weichao,WANG Liangmo,YIN Zhaoping,et al.Optimization design for powertrain mounting system of a hybrid electric vehicle via genetic algorithm [J].Journal of Vibration and Shock,2015,34(8):209-213.

[5] 薛華,劉志強(qiáng),劉巖,等.基于MATLAB的動(dòng)力總成懸置系統(tǒng)解耦優(yōu)化[J].噪聲與振動(dòng)控制,2015,35(2):65-68.

XUE Hua,LIU Zhiqiang,LIU Yan,et al.Decoupling and optimal design of a powertrain mount system based on MATLAB[J].Noise and Vibration Control,2015,35(2):65-68.

[6] 運(yùn)偉國(guó),王邵斌,楊少華.重型汽車(chē)動(dòng)力總成懸置NVH性能研究[J].噪聲與振動(dòng)控制,2014,34(5):99-101.

YUN Weiguo,WANG Shaobin,YANG Shaohua.NVH performance study of a heavy-duty truck's power train mount[J].Noise and Vibration Control,2015,35(2):65-68.

Vibrationisolation analysis and optimization of excavatorpowertrain mounting system

A new developed excavator appears obvious shaking under the idle condition,based on this condition built a 6-degree-of-freedom model of power train mounting system.Based on the principle of energy decoupling,take the dynamic stiffness of absorber as variables,modal frequency as constraint condition and energy decoupling on key direction as the objective functions optimize design the power train mounting system.After optimization energy decoupling on key direction was maximum increased 20.2%.Tested before and after optimization,according to the results after optimization the isolation was improved.

powertrain mounting system; vibration; energy decoupling; Matlab

國(guó)家“八六三”高技術(shù)計(jì)劃資助項(xiàng)目(2014AA041502)

邢樹(shù)鑫(1982-),男,高級(jí)工程師。E-mial：xingsx@liugong.com

U 461.1

A

1672-5581(2016)01-0017-04