一種LCCL濾波器及其在半橋電力有源濾波器中的應用

方旌揚 肖國春 鄭力夫 鄭家祿

?

一種LCCL濾波器及其在半橋電力有源濾波器中的應用

方旌揚 肖國春 鄭力夫 鄭家祿

（西安交通大學電氣工程學院 西安 710049）

提出一種新型高階電力濾波器，將其命名為LCCL濾波器。與傳統的LCL濾波器相比，LCCL濾波器通過在網側電感支路并聯一個小電容，使網側電感與并聯電容在開關頻率處發生并聯諧振。諧振使LCCL濾波器網側支路在開關頻率處呈現無窮大的阻抗，相比LCL濾波器可以更好地抑制開關頻率附近電網電流紋波，減小電網電流THD。與LLCL濾波器相比，LCCL濾波器具有較好的抑制參數變化的能力，在考慮電網內阻抗時，擁有更好的高頻紋波抑制性能。同時，可以更容易地進行基于電容電流反饋有源阻尼的控制器設計。LCCL濾波器作為電壓源型逆變器（VSI）與電網的接口，可應用于PWM整流器、有源電力濾波器（APF）和通用電能質量控制器（UPQC）等多種場合。通過以半橋APF為例，討論了LCCL濾波器的參數選擇方法和控制器設計。最后，通過仿真和實驗驗證了LCCL濾波器的可行性。

LCCL濾波器 LLCL濾波器 LCL濾波器 半橋電力有源濾波器 并聯諧振

0 引言

近年來，可再生能源分布式發電的發展使電壓源型逆變器（Voltage Source Inverter, VSI）得到了廣泛的應用[1-6]。隨著人們生產生活對電能質量要求的不斷提高，旨在消除諧波電流問題的有源電力濾波器（Active Power Filter, APF）[7,8]及綜合解決電能質量問題的通用電能質量控制器（Unified Power Quality Controller, UPQC）[9]也受到越來越多的關注。在這些裝置中，電網和變流器之間都需要接入無源濾波器作為兩者的接口來抑制PWM技術帶來的開關紋波。

傳統的無源濾波器采用單電感。為了減小電感成本和體積，同時提升濾波器對于高頻紋波的抑制性能，LCL濾波器越來越多的被采用[10-17]。LCL濾波器存在諧振問題。解決諧振問題的方法大致分為兩種：①加入電阻進行無源阻尼[5,6,15]；②利用控制算法進行有源阻尼[2-4,7-14,17]。相比而言，有源阻尼不需要額外電阻，可以減小裝置成本、功耗和體積，因此得到越來越多的應用。有源阻尼的實現方法很多，包括有電容電流進行反饋控制[2-4,8-10,13]、電感電流加權控制[11]、利用現代控制理論進行極點配置[12]以及通過逆變器側電流進行反饋控制[17-20]。在諸多方法中，反饋電容電流實現簡便，物理意義清晰，因而得到廣泛應用。

文獻[5]提出一種LLCL型濾波器，該濾波器通過在LCL濾波器電容支路串聯小電感實現電容支路在開關頻率處的串聯諧振，從而更好地抑制開關頻率附近紋波進入電網。在文獻[6]中，串聯諧振的支路數進一步增加，其目的是增加多個高頻紋波抑制頻率點，然而系統參數設計過程復雜。應用于并網逆變器時，LLCL濾波器實現了網側電感量的減小和濾波性能的提升。受LLCL濾波器的啟發，本文提出一種LCCL濾波器，該濾波器具有與LLCL濾波器相同的優點。除此以外，與LLCL濾波器相比，LCCL濾波器具有更好地抑制參數變化的能力，在考慮電網內阻抗時擁有更強的高頻紋波抑制性能。同時，可以更合理地進行基于電容電流反饋有源阻尼的控制器設計。

本文介紹了LCCL濾波器的原理，重點分析所提出的LCCL濾波器相比LCL濾波器和LLCL濾波器的優勢。并以半橋APF為例，進行參數選取和基于該參數下的控制器設計，參數選擇和控制器設計方法不僅限于某一個特定的應用場合，只要是并網逆變器均可采用。最后，通過仿真和實驗驗證了LCCL濾波器的可行性。

1 LCCL濾波器理論分析

1.1 LCL濾波器和LLCL濾波器

單相VSI等效電路的LCL濾波器原理如圖1所示。圖1中，是逆變器側電感，g是網側電感，是濾波電容，i是逆變器輸出電壓，s是電網電壓。LCL濾波器的主要目的是抑制開關動作所產生的逆變器側電壓i中的高頻分量對電網電流g的影響。

圖1 LCL濾波器原理

逆變器側輸出電壓到網側電流傳遞函數為

逆變器側輸出電壓到逆變電流傳遞函數為

（2）

基于LLCL濾波器的VSI在LCL濾波器的電容支路加入一個小電感f，構成串聯諧振支路，則LLCL濾波器原理如圖2所示。

圖2 LLCL濾波器原理

LLCL濾波器的原理[5]為單相VSI輸出的諧波電流頻譜主要集中在開關頻率處。因此，網側電感和濾波電容的設計主要針對開關頻率處紋波的抑制。通過在電容支路引入一個電感，實現開關頻率處的串聯諧振，達到開關頻率處陷波的作用。因此，網側電感設計僅需考慮開關頻率倍頻處的紋波抑制。

LLCL濾波器逆變側輸出電壓到網側電流的傳遞函數為

逆變側輸出電壓到逆變電流的傳遞函數為

（4）

LCL濾波器和LLCL濾波器伯德圖對比如圖3所示。LCL濾波器參數見表1系統主電路參數。LLCL濾波器在LCL濾波器參數基礎上增加0.1mH串聯電感f。圖3a是逆變側輸出電壓到逆變側電流傳遞函數伯德圖對比，由圖3可見兩者基本重合。

表1 系統主電路參數

Tab.1 Main circuit parameters of the system

（a）逆變電壓到逆變電流

（b）逆變電壓到網側電流

圖3 LCL濾波器與LLCL濾波器伯德圖對比（=1mF，=g=3mH，f=0.1mH）

Fig.3 Comparison of Bode plots between LCL filter and LLCL filter (=1mF，=g=3mH，f=0.1mH)

圖3b是逆變側輸出電壓到網側電流傳遞函數的伯德圖對比。可以看出LLCL濾波器在開關頻率處增益非常低，從而很好地實現開關頻率處的紋波抑制。在低頻區域兩者頻率特性基本重合，因此可以簡化LLCL濾波器參數選擇和基于無源阻尼的控制器設計。在高頻區，LLCL濾波器以-20dB/dec的斜率衰減，其衰減速率較LCL濾波器的-60dB/dec小。因此，在保持逆變電流與LCL濾波器基本相同的情況下，LLCL濾波器網側電流開關頻率附近紋波含量大大減小。

1.2 LCCL濾波器原理

LCCL濾波器的想法源于LLCL濾波器。為了實現開關頻率附近紋波電流流入電容支路，除了可以利用串聯諧振原理，使電容支路阻抗在開關頻率處為零，也可以利用并聯諧振原理，使網側電感支路在開關頻率處阻抗無窮大。圖4為LCCL濾波器原理。

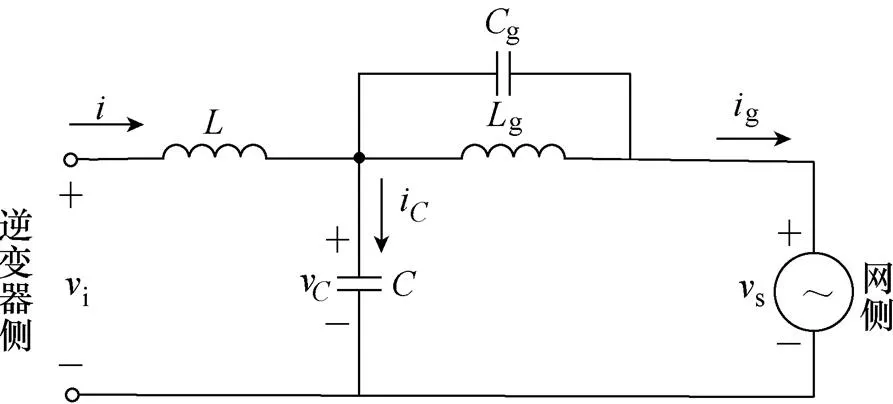
圖4 LCCL濾波器原理

設計LCCL濾波器使網側電感g和網側電容g在開關頻率處實現并聯諧振，支路阻抗為無窮大，從而阻止開關頻率附近紋波電流進入電網。逆變器側輸出電壓到網側電流的傳遞函數為

逆變器側輸出電壓到逆變電流的傳遞函數為

（6）

2 LCCL與LCL、LLCL濾波器的對比

圖5為LCCL與LCL、LLCL濾波器伯德圖對比。LCCL濾波器參數見表1。

（a）LCCL與LCL

（b）LCCL與LLCL圖5 LCCL與LCL、LLCL濾波器伯德圖對比（=1mF，=g=3mH，g=37.5nF）

Fig.5 Comparison of Bode plots among LCCL filter, LCL filter and LLCL filter (=1mF，=g=3mH，g=37.5nF)

由圖5a可見，LCCL濾波器擁有很強的開關頻率處紋波抑制能力。高頻區域具有-20dB/dec幅頻衰減斜率，低頻響應與LCL濾波器重合。因此，便于仿照LCL濾波器進行參數選擇和控制器設計。根據圖5b，LCCL濾波器和LLCL濾波器伯德圖基本重合。由于具有與LLCL濾波器相同的頻率特性，LCCL濾波器也具有LLCL濾波器的優點。

2.1 濾波器參數變化分析對比

當網側支路并聯電容g在0.95～1.05倍額定值之間變化時，LCCL濾波時逆變器側電壓到網側電流傳遞函數，即g變化時LCCL伯德圖如圖6所示。由圖6可見，電容值的波動對于LCCL濾波器的諧振頻率（4 110Hz）影響較小（4 060Hz），同時在開關頻率處濾波器保持高紋波抑制能力（-103dB）。

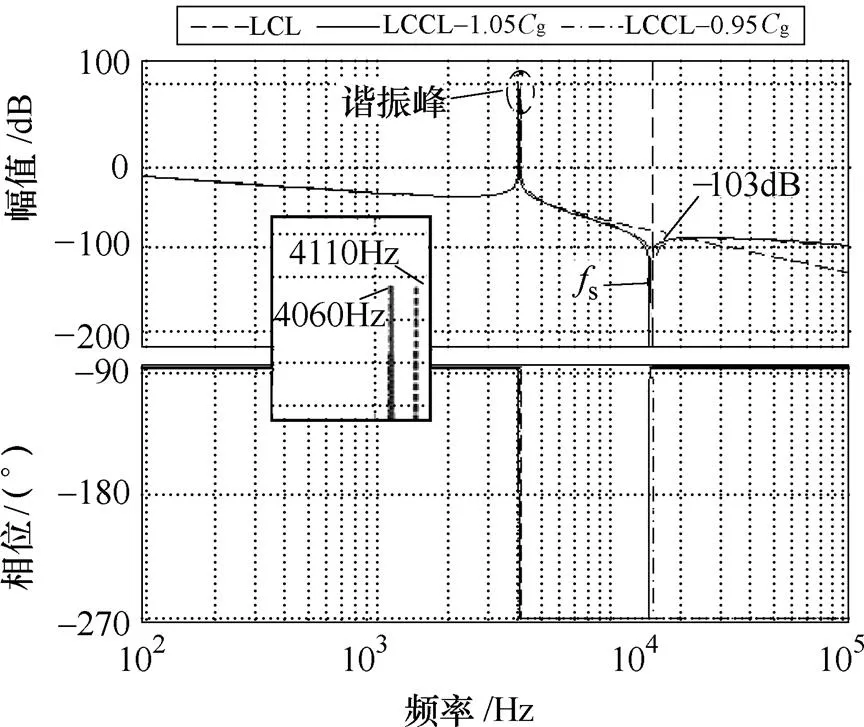
圖6 Cg變化時LCCL伯德圖（C=1mF, L=Lg=3mH, Cg=(0.95～10.5)×37.5nF）

在實際工程應用中，較電容而言，電感的取值具有更大的變化。當加入的串聯電感在0.9～1.1倍額定值f之間變化時，LLCL濾波時逆變器側電壓到網側電流傳遞函數，即f變化時LLCL伯德圖如圖7所示。由圖7可知，電感f的變化導致了諧振峰頻率的變化（3.9kHz）。電感量增大時，LLCL濾波器陷波頻率將會降低。隨著陷波頻率的變化，LLCL濾波器在開關頻率處的紋波抑制能力減弱（-93dB）。此外，濾波器參數變化對于低頻特性影響較小。

圖7 Lf變化時LLCL伯德圖（C=1mF, L=Lg=3mH, Lf=(0.90～1.10)×0.1mH）

2.2 考慮電網內阻抗LCCL濾波器的魯棒性分析

在實際應用中，需要考慮電網內阻抗。考慮電網內阻抗LCCL濾波器原理如圖8所示。

只考慮電網內電感時，逆變側輸出電壓到電網電流的傳遞函數如式（7）所示。考慮電網內電感LCCL濾波器伯德圖如圖9所示。圖9中，電網電感s=0.3mH。

圖9 考慮電網內電感LCCL濾波器伯德圖（C=1mF, L=Lg=3mH, Cg=37.5nF）

由圖9可以看出，考慮電網內電感時濾波器階數增高為5階，同時出現新的諧振峰。雖然諧振峰的頻率在開關頻率的3倍以上（50kHz），但是高頻諧振峰會對系統穩定性產生影響。諧振峰過后幅頻特性斜率變為-60dB/dec。可見，電網內電感對于LCCL濾波器抑制更高頻率（s＞70kHz）噪聲有利。

在實際電網中，除了存在內電感外，也包含內電阻。電網內電阻可以對高頻諧振峰帶來阻尼作用。在考慮電網內電阻時，式（7）的傳遞函數變為式（8）的形式。考慮電網內阻抗LCCL濾波器伯德圖如圖10所示，圖10a電網內電阻s=0.1W。由圖10可見，濾波器可以實現良好的高頻諧振抑制效果（-35dB以下）；由圖10b可見，即使電網內電阻只有0.05W，也不會影響系統的穩定性（-25dB以下）。同時，電網內阻抗的加入不會影響LCCL濾波器開關頻率處紋波抑制能力。

圖11為電網內電感變化時LCCL濾波器伯德圖。由圖11可見，電網內電感變化時，LCCL濾波器對開關頻率處具有高紋波抑制能力。隨著電網內電感的增大，高頻諧振峰前移。此時，LCCL濾波器具有更接近LCL濾波器的高頻紋波抑制能力（＞3s）。

（a）Rs=0.1W （b）Rs=0.05Ω

圖11 電網內電感變化時LCCL濾波器伯德圖（C=1mF, L=Lg=3mH, Cg=37.5nF, Rs=0.3W）

實際設計中需要避免高頻諧振峰頻率與開關頻率倍數相重合。圖11中，s=1.2mH時高頻諧振峰頻率接近2s。為避免這種情況出現，在電網內電感已知的前提下，可以在設計時根據伯德圖調整參數，避免這種情況的出現，從而保證LCCL濾波器高頻紋波抑制能力。

2.3 基于電容電流反饋有源阻尼控制算法的對比

基于電容電流反饋有源阻尼的LCCL濾波器控制結構如圖12所示。圖12中，ref()為參考電流，g()為網側電流，G()為電流環控制器，H1為電容電流反饋系數，H2為網側電流反饋系數，PWM為逆變器放大倍數。

為分析簡便，令PWM=1。結合圖8和文獻[4]的分析思路，逆變器輸出電壓i()中包含基波、低次諧波電壓分量和開關倍頻附近紋波電壓分量。由于控制器帶寬小于諧振峰頻率，所以考慮系統對于諧振峰附近頻率處阻尼特性時且當電容電流反饋系數H1=0，逆變器輸出電壓i()可以忽略不計。令電容電壓為v()，此時網側電流為

H1≠0時，i()=-H1i()。網側電流為

（10）

這相當于給電容支路并聯一個電阻，電阻值為

對于圖2中的LLCL濾波器，采用同樣的分析思路，令vf()為諧振峰附近頻率處串聯電感上的電壓，電容電流反饋系數H1=0時，網側電流為

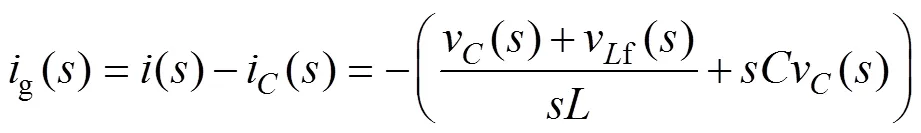
當H1≠0時，網側電流變為

（13）

因此，LLCL濾波器應用電容電流反饋有源阻尼控制算法時其等效并聯阻抗大小為

（14）

可見，LLCL濾波器采用電容電流反饋有源阻尼時相當于給電容支路并聯了一個頻變電阻。在H1=15時，LCCL濾波器和LLCL濾波器采用電容電流反饋有源阻尼時其等效電阻伯德圖如圖13所示。

圖13 等效電阻伯德圖（C=1mF, L=Lg=3mH, Cg=37.5nF, Lf=0.1mH, Hi1=15）

在電路參數給定的情況下，LCCL具有恒定的阻尼電阻。LLCL的電阻阻值隨著頻率的變化逐漸由正電阻變為負電阻。在高頻負電阻區域，隨著頻率的增大，電阻阻值絕對值增長很快。由于阻尼電阻與電容支路并聯，電阻增大減弱了阻尼效果，這一點對高諧振峰頻率控制器的設計不利。

令LCCL濾波器等效并聯電阻為，其逆變器側輸出電壓到電網電流傳遞函數變為

LLCL濾波器等效并聯電阻為′，則其逆變器側輸出電壓到電網電流傳遞函數為

（16）

考慮一種情況：g=1mH，g=112.5nF，H1=15，其他參數保持不變見表1。由式（11）和式（14）可知，在諧振頻率處等效電阻200W，等效并聯電阻′=-600W。

圖14為電容電流反饋有源阻尼時LCCL濾波器與LLCL濾波器伯德圖對比。由圖14可見，在諧振峰頻率處，LCCL濾波器的阻尼效果（-26.5dB）明顯優于LLCL濾波器（-15.5dB）。

圖14 電容電流反饋有源阻尼時LCCL濾波器與LLCL濾波器伯德圖對比（C=1mF, L=Lg=3mH, Cg=112.5nF, Lf=0.1mH）

3 仿真和實驗

為驗證LCCL濾波器的可行性，本文以半橋APF為例進行濾波器參數選擇和控制器設計。由圖5b可知，LCCL濾波器和LLCL濾波器擁有同樣開關頻率處紋波抑制能力和基本重合的伯德圖。因此LCCL濾波器可以完全借鑒LLCL濾波器的參數設計思路來實現減小網側電感量的目的。與文獻[5]設計過程不同之處在于：①需要選擇網側并聯電容與網側電感諧振；②不需要串聯電感加入濾波電容支路；③可以采用基于電容電流反饋有源阻尼的方法進行控制器設計。

半橋APF系統結構如圖15所示。由圖15可知，半橋APF包含兩個直流側電容1、2和兩個開關管VT1、VT2（IGBT）。LCCL濾波器將APF與電網相連接，通過控制APF注入電網非線性負載消耗的諧波電流分量，實現電網電流波形的正弦化。系統主電路參數見表1。

圖15 半橋APF系統結構

3.1 濾波器參數選擇和控制器設計

（1）總電感量g。LCCL濾波器參數選取需要滿足低次諧波電流跟蹤控制要求和高頻紋波電流抑制要求，同時濾波器損耗和無功損耗盡可能小。在低頻區域，濾波器可以等效為單電感g進行設 計[16]。本文選擇總電感量g6mH。

（2）濾波電容。電容產生的無功功率損耗不超過系統額定功率的5%[15]，則

（3）電感分配g、。為了實現較低的諧振頻率，從而更好地衰減高頻紋波，將兩個電感和g取為同等大小[8]，g3mH。

（4）諧振頻率res。為了適用于電容電流反饋有源阻尼的控制方法，避免因參數變化引起的諧振峰偏移導致系統不穩定[2]，保證系統的控制能力。諧振頻率設定為

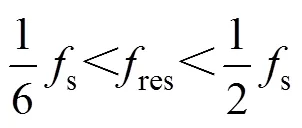
最終選擇，1mF，保證諧振頻率res=4 109Hz。

（5）網側并聯電容g。g的選取需要使網側支路發生并聯諧振，滿足

式中，代入s=15kHz，得到g=37.5nF。

由圖5a可知，LCCL濾波器位于開關頻率處的諧振只產生陷波特性。除此以外，開關頻率比諧振峰頻率大很多（s＞3r），故小電容g的加入不影響系統控制器帶寬和有源阻尼的效果。進行基于電容電流反饋有源阻尼的控制器設計，仍然按照LCL濾波器的設計思路。考慮延時，半橋APF電流環域控制結構如圖16所示。圖16中，ref()是參考電流的變換，G()是電流環數字控制器，-1是采樣和計算帶來的延時，ZOH是輸出延時（用零階保持器代替）。

系統控制參數見表2[13]。表2中，P為電流環控制器，c為系統帶寬。

圖16 半橋APF電流環z域控制結構

表2 系統控制參數

Tab.2 Control parameters of the system

電流環開環伯德圖如圖17所示，滿足基波處高增益30dB、系統帶寬1 250Hz（補償25次及以下諧波）、相位裕度42.6°、幅值裕度GM1＞3dB和GM2＜-3dB的要求。

圖17 電流環開環伯德圖

電壓控制外環設計基于將電流內環等效為一個一階慣性環節，慣性時間常數為i1/c。半橋APF電壓環控制結構如圖18所示。通過鎖相電網電壓得到基波正弦、余弦信號。諧波提取采用正弦、余弦三角函數法[18]。直流側上下橋臂電壓和參考指令減去直流側實際電壓之和得到直流電壓和的偏差，該偏差經過PI調節器控制疊加到有功功率電流指令上。同時取直流側上、下橋臂電壓差經比例控制疊加到電流參考指令上從而實現直流側均壓控制。PI控制器和比例控制器參數設計結果為，=0.2，=0.15，=0.1。

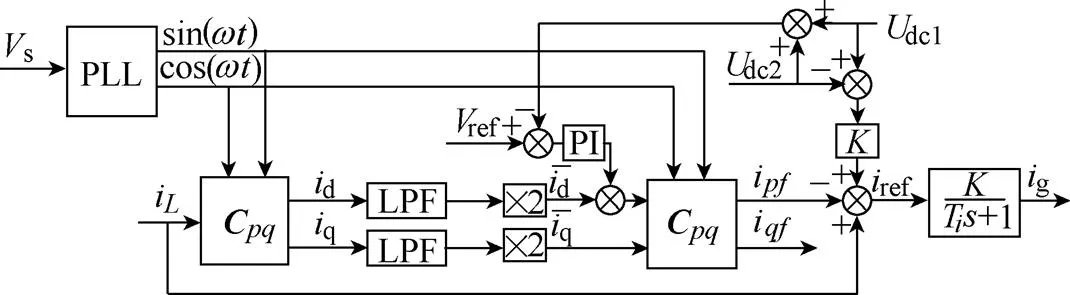
圖18 半橋APF電壓環控制結構

3.2 仿真

搭建基于Matlab/Simulink的仿真模型。系統主電路參數見表1，控制器參數見表2。負載采用不可控整流橋接電容性負載模擬開關電源類電源。補償前的負載電流仿真波形如圖19所示。負載電流總諧波畸變率（Total Harmonic Distortion, THD）如圖20所示，補償前電網電流THD=22.53%。采用LCL濾波器，并使用基于電容電流反饋有源阻尼技術的控制器進行諧波補償，LCL濾波器補償后電網電流仿真波形如圖21所示。LCL濾波器補償器補償后電網電流THD如圖22所示，補償后電網電流THD= 4.14%。由圖22可見，在開關頻率附近（300次諧波）存在較高的開關紋波。

圖19 負載電流仿真波形

圖20 負載電流THD

圖22 LCL濾波器補償后電網電流THD

采用LLCL濾波器代替LCL濾波器，除增加0.1mH串聯電感f外保持濾波器參數和控制參數不變，LLCL濾波器補償后電網電流仿真波形如圖23所示。其THD如圖24所示，補償后電網電流THD= 3.91%。

圖23 LLCL濾波器補償后電網電流仿真波形

圖24 LLCL濾波器補償后電網電流THD

可見，LLCL濾波器可以很好地抑制開關頻率附近的紋波，補償后電網電流THD有所下降。然而，基于1.3節分析可知，對于LLCL濾波器，電容電流反饋產生的阻尼效果會隨著頻率的增高而變差。因此，基于電容電流反饋有源阻尼的LLCL濾波器設計過程需要考慮更多的因素。由圖24發現在二倍開關頻率附近出現了開關動作帶來的高頻紋波。

采用LCCL濾波器結合電容電流反饋有源阻尼技術，LCCL濾波器補償后電網電流仿真波形如圖25所示。其THD如圖26所示，補償后電網電流THD=3.38%。

圖25 LCCL濾波器補償后電網電流仿真波形

圖26 LCCL濾波器補償后電網電流THD

相比LCL濾波器，LCCL濾波器開關頻率處紋波抑制能力明顯增強，然而二倍開關頻率處紋波電流有所增大。LCCL濾波器補償后，電網電流THD是最低的。

并聯電容g在1±20%發生變化時LCCL濾波器補償后電網電流THD如圖27所示。由圖27可見，由于諧振頻率的變化，濾波后電網電流出現開關次紋波，但LCCL濾波器開關頻率處紋波抑制能力仍然強于LCL濾波器。由此可見，LCCL濾波器具有較好的魯棒性。

（a）1.2g

（b）0.8g

圖27g(1±20%)時LCCL濾波器補償后電網電流THD

Fig.27 THD of source current compensated by LCCL filter withg(1±20%)

考慮電網內阻抗（0.3mH電感+0.1W電阻），LCCL濾波器補償后電網電流THD如圖28所示。由圖28可見，電網內阻抗并不影響LCCL濾波器開關附近紋波的濾波性能。

圖28 考慮電網內阻抗LCCL濾波器補償后電網電流THD

3.3 實驗結果

搭建以DSP（TMS320F28335）為控制器的實驗平臺，控制器參數見表2。電源電壓和負載電流實驗波形及負載電流THD如圖29所示。負載電流THD=32.7%。

采用LCL濾波器和電容電流反饋有源阻尼的控制方法，LCL濾波后電源電壓和電網電流實驗波形及電網電流THD如圖30所示。電網電流THD=3.1%。進一步測量電網電流開關頻率處紋波電流，大小為0.05A。

（a）電源電壓和負載電流實驗波形

（b）負載電流THD

圖29 電源電壓和負載電流實驗波形及負載電流THD

Fig.29 Experimental waveforms of source voltage and load current and THD of load current

（a）電源電壓和電網電流實驗波形

（b）電網電流THD

圖30 LCL濾波后電源電壓和電網電流實驗波形及電網電流THD

Fig.30 Experimental waveforms of source voltage and source current and THD of source current compensated by LCL filter

采用LCCL濾波器和電容電流反饋有源阻尼控制方法，LCCL濾波后電源電壓和電網電流實驗波形及電網電流THD如圖31所示。補償后電網電流THD=2.4%。進一步測量電網電流開關頻率處紋波電流，大小為0.01A。

（a）電源電壓和電網電流實驗波形

（b）電網電流THD

圖31 LCCL濾波后電源電壓和電網電流實驗波形及電網電流THD

Fig.31 Experimental waveforms of source voltage and source current and THD of source current compensated by LCCL filter

綜上，LCCL濾波器實現了開關頻率附近紋波抑制良好，減小了補償后電網電流THD。仿真和實驗結果表明LCCL濾波器是可行的，而且性能較LCL濾波器更為優越。

4 結論

本文提出一種高階LCCL濾波器，在對其原理進行分析的基礎上，論述了LCCL濾波器的優勢。

相比傳統的LCL濾波器，LCCL濾波器通過增加一個小電容與網側電感并聯形成開關頻率處的并聯諧振，從而增強開關頻率附近紋波抑制能力，減小電網電流THD。相比LLCL濾波器，LCCL濾波器擁有較好的魯棒性，考慮電網內阻抗時具有更強的高頻紋波抑制能力。同時，可以合理地進行基于電容電流反饋有源阻尼控制算法的控制器設計。本文以半橋APF為例給出了濾波器參數選擇方法和控制器設計結果。最后，通過仿真和實驗驗證了LCCL濾波器的可行性。

參考文獻：

[1] 邱曉明, 王明渝, 胡文翠, 等. LLCL濾波的單相光伏并網逆變器控制技術研究[J]. 電力系統保護與控制, 2013, 41(10): 74-79.

Qiu Xiaoming, Wang Mingyu, Hu Wencui, et al. LLCL filter based single-phase photovoltaic grid- connected inverter control strategy[J]. Power System Protection and Control, 2013, 41(10): 74-79.

[2] Pan D, Ruan X, Bao C, et al. Capacitor-current- feedback active damping with reduced computation delay for improving robustness of LCL-type grid- connected inverter[J]. IEEE Transactions on Power Electronics, 2014, 29(7): 3414-3427.

[3] Bao C, Ruan X, Wang X, et al. Step-by-step controller design for LCL-type grid-connected inverter with capacitor-current-feedback active- damping[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1239-1253.

[4] He J, Li J. Generalized closed-loop control schemes with embedded virtual impedances for voltage source converters with LC or LCL filters[J]. IEEE Transa- ctions on Power Electronics, 2012, 27(4): 1850-1861.

[5] Wu W, He Y, Blaabjerg F. An LLCL power filter for single-phase grid-tied inverter[J]. IEEE Transactions on Power Electronics, 2012, 27(2): 782-789.

[6] Xu J, Yang J, Ye J, et al. An LTCL filter for three- phase grid-connected converters[J]. IEEE Transa- ctions on Power Electronics, 2014, 29(8): 4322-4338.

[7] Liu Q, Peng L, Kang Y, et al. A novel design and optimization method of an LCL filter for a shunt active power filter[J]. IEEE Transactions on Indu- strial Electronics, 2014, 61(8): 4000-4010.

[8] Tang Y, Loh P, Wang P, et al. Generalized design of high performance shunt active power filter with output LCL filter[J]. IEEE Transactions on Industrial Electronics, 2012, 59(3): 1443-1452.

[9] Khadkikar V. Enhancing electric power quality using UPQC: a comprehensive overview[J]. IEEE Transa- ctions on Power Electronics, 2012, 27(5): 2284-2297.

[10] 伍小杰, 孫蔚, 戴鵬, 等. 一種虛擬電阻并聯電容有源阻尼法[J]. 電工技術學報, 2010, 25(10): 122-128.

Wu Xiaojie, Sun Wei, Dai Peng, et al. An active damping method of virtual resistor in parallel with capacitor[J]. Transactions of China Electrotechnical Society, 2010, 25(10): 122-128.

[11] He N, Xu D, Zhu Y, et al. Weighted average current control in a three-phase grid inverter with an LCL filter[J]. IEEE Transactions on Power Electronics, 2013, 28(6): 2785-2797.

[12] 李賓, 姚文熙, 杭麗君等. 基于狀態觀測器的LCL濾波器型并網逆變器狀態反饋最優化設計[J]. 電工技術學報, 2014, 29(6): 80-90.

Li Bin, Yao Wenxi, Hang Lijun, et al. Optimized design of state variable feedback of grid-connected inverter with LCL-filter based on state observer[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 80-90.

[13] Bao C, Ruan X, Wang X, et al. Design of injected grid current regulator and capacitor-current-feedback active-damping for LCL-type grid-connected inver- ter[C]//IEEE Conference on Energy Conversion Con- gress and Exposition, Raleigh, NC, 2012: 579-586.

[14] 武健, 馬驍, 侯睿, 等. 基于遺傳算法的有源濾波器LCL輸出濾波器優化設計[J]. 電工技術學報, 2011, 26(5): 159-177.

Wu Jian, Ma Xiao, Hou Rui, et al. Optimization of APF LCL output filter based on genetic algorithm[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 159-177.

[15] Liserre M, Blaabjerg F, Hansen S. Design and control of an LCL-filter based active rectifier[J]. IEEE Transactions on Industry Applications, 2005, 41(2): 1281-1291.

[16] 張興, 張崇巍. PWM整流器及其控制[M]. 北京: 機械工業出版社, 2012.

[17] 闞加榮, 謝少軍, 姚志壘, 等. LCL濾波并網逆變器的進網電流相位矯正技術[J]. 電力系統自動化, 2012, 36(14): 166-171.

Kan Jiarong, Xie Shaojun, Yao Zhilei, et al. A phase correction technique for grid side current of grid- connected inverter with LCL filter[J]. Automation of Electric Power Systems, 2012, 36(14): 166-171.

[18] 何益宏. 通用電能質量控制器檢測和控制方法的研究[D]. 西安: 西安交通大學, 2003.

[19] 侯睿, 武健, 徐殿國. 并聯有源濾波器LCL濾波器特性分析及設計方法[J]. 電工技術學報, 2014, 29(10): 191-198.

Hou Rui, Wu Jian, Xu Dianguo. Characteristics and design methods of LCL filter in shunt active power filter[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 191-198.

[20] 莊超, 葉永強, 趙強松, 等. 基于分裂電容法的LCL并網逆變器控制策略分析與改進[J]. 電工技術學報, 2015, 30(16): 83-93.

Zhuang Chao, Ye Yongqiang, Zhao Qiangsong, et al. Analysis and improvement of the control strategy of LCL grid-connected inverter based on split- capacitor[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 83-93.

An LCCL Filter for a Half-Bridge Active Power Filter

（School of Electrical Engineering Xi’an Jiaotong University Xi’an 710049 China）

In this paper, a novel high order power filter is proposed, named the LCCL filter. Compared with the traditional LCL filter, the LCCL filter composes a parallel resonant branch loop at the switching frequency by paralleling a small capacitor with the line side inductor. The parallel resonance enables the line side branch loop to exhibit infinite impedance at the switching frequency. Particularly, it can attenuate the switching frequency current ripple components much better than the LCL filter, thus decreases THD in source current. Compared with the LLCL filter, the LCCL filter performs well considering the case where parameters are not fixed and exhibits better attenuation ability in the high frequency domain when the source impedance is considered. Besides, a capacitor current feedback based active damping controller is easy to design on the LCCL filter. As an interface between voltage source inverter (VSI) and the grid, the LCCL filter can be applied to the PWM rectifier, active power filter (APF), and unified power quality controller (UPQC). A half-bridge APF is taken as an example in this paper to discuss the parameter selection method and the controller design method based on the LCCL filter. At last, simulation and experimental results validate the feasibility of the proposed LCCL filter.

LCCL filter, LLCL filter, LCL filter, half-bridge active power filter, parallel resonance

TM46

國家自然科學基金資助項目（51277146）。

2014-09-17 改稿日期 2015-01-16

方旌揚 男，1992年生，碩士研究生，研究方向為電能質量分析及其控制。E-mail: 437214193@qq.com（通信作者）

肖國春 男，1965年生，教授，博士生導師，研究方向為電能質量分析與控制技術，電力電子系統的建模、仿真與控制，分布式發電技術，電力電子裝置設計及應用。E-mail: xgc@mail.xjtu.edu.cn