標準BP神經網絡算法和附加動量法在沉降監測中的應用研究

李波,柳華橋,戴鑫,賈志強

(天津市測繪院,天津 300381)

標準BP神經網絡算法和附加動量法在沉降監測中的應用研究

李波1?,柳華橋2,戴鑫3,賈志強4

(天津市測繪院,天津 300381)

在沉降監測工程實踐中,由于采用的預測方法和項目沉降趨勢的不同,預測結果的精度會有差異。而隨著應用的不斷深入,對現有算法進行改進以發揮算法的優勢,成為目前預測算法研究的主流。在本文的研究中,編程實現了標準BP神經網絡算法和附加動量法。通過研究學習率對標準BP神經網絡算法的影響,確定學習率的大小。然后,研究了動量項對附加動量法收斂速度的影響,確定了動量項的取值。最后,對兩種算法的穩定性和算法的效率以及預測精度等方面進行比較,探究兩種算法的特點。

沉降監測;BP神經網絡;附加動量法

1　引 言

人工神經網絡是目前在變形監測領域廣泛使用的預測方法。這種算法的優點是,對于復雜的非線性系統,能進行很好逼近,獲得較高的擬合精度和預測精度。人工神經網絡中使用最多的是BP神經網絡。因為BP神經網絡對變形的內部機制沒有要求,可以在不清楚變形機制的情況下進行變形預測,使得這種方法得到了大量的研究和應用。

BP神經網絡也有很多缺點,主要表現在:誤差下降過程中,容易陷入局部極小值;誤差收斂速度慢,耗時較長;發現變形機制的泛化能力一般;構建BP神經網絡沒有統一的原則[1]。本文在實現標準BP神經網絡和附加動量的BP神經網絡算法的基礎上,對兩種算法的穩定性和算法的效率以及對樣本數據的預測精度等方面進行比較,得出有指導意義的結論,指導工程實踐。

2　人工神經網絡算法

2．1人工神經網絡算法簡介

人工神經網絡算法模仿大腦神經元對刺激的應激機制,一般由3層組成:輸入層、隱層、輸出層。輸入信號由輸入層向隱層傳輸,經過隱層激活函數的作用,輸出到輸出層,再次經過激活函數的作用,得出網絡的輸出。通過正向學習獲得的誤差,利用梯度下降法進行反向傳播,調整神經元之間的權值和閾值,使得輸出的誤差項達到要求,如圖1所示。

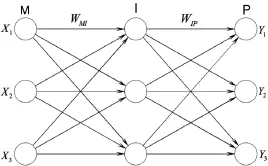
圖1　BP神經網絡結構示意圖

2．2標準BP神經網絡算法

設輸入層的輸入信號個數有M個,隱層有I個節點,輸出層有P個節點。輸入層的輸入用XM表示,輸入層和隱層之間的權值用WMI表示,隱層和輸出層之間的權值用WIP表示。輸出層的輸出用YP表示。在樣本的學習過程中,各層的輸入和輸出由下式計算:

那么,輸出層第p個神經元的學習誤差為:

2．3 附加動量的BP神經網絡

所謂附加動量法是將權值調整量加上部分的上次權值調整量,作為一個整體,當作這次學習的權值調整量,這也是附加動量法和標準BP算法的區別所在。權值調整的公式如下所示:

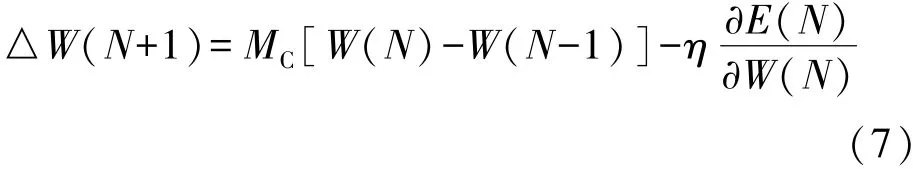
在上式中,MC表示加入的動量系數,N為訓練的次數。

由上式可知,MC=0時,本次學習的權值調整量是按照梯度下降法確定。當網絡的訓練權值接近誤差曲面的局部極小值時,局部梯度值變得很小。加入動量項可以避免陷入局部極小值的可能。

3　兩種算法的比較與分析

3．1數據準備和網絡結構設計

本文的樣本數據采用天津市某高架橋橋墩沉降監測數據,通過傳統水準測量的方法獲得,樣本共有24期。前20期為訓練樣本,后4期為預測樣本。本文采用的樣本數據如表1所示:

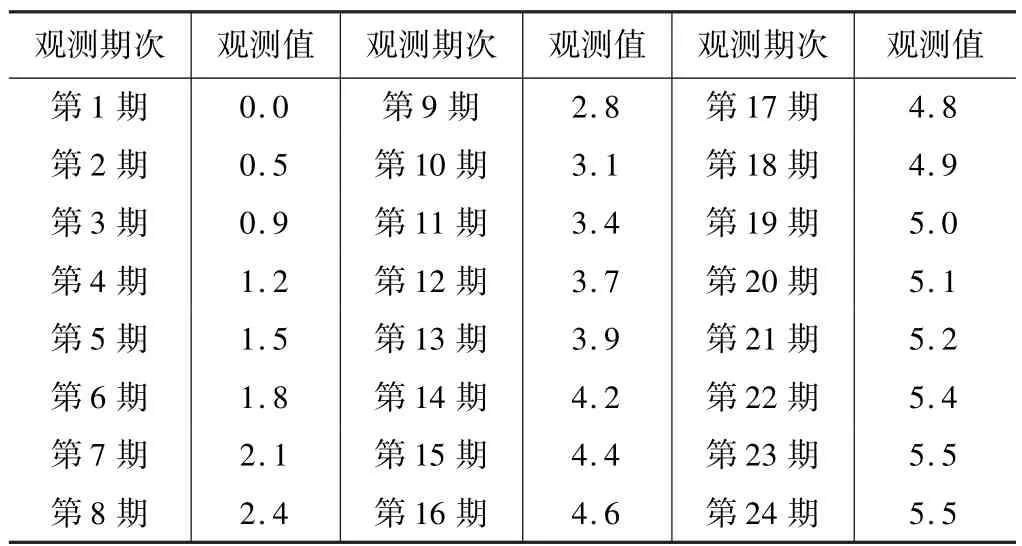
樣本數據　表1

根據沉降數據的特征,將BP神經網絡輸入層和輸出層的神經元數量均設置為1個,分別對應觀測期數和沉降值。

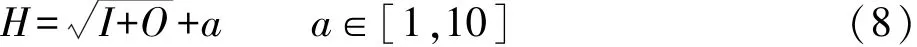
由上述隱層節點數量的經驗公式,將本文的隱層設計為單層,隱層節點數為4個。

3．2學習率對標準BP算法收斂速度的影響

權值的調整量是學習率和局部梯度的內積,因此學習率的大小直接影響權值調整量的多少。作者選取了5組學習率,分別是:0．10、0．25、0．40、0．55、0．70、0．85。針對每個學習率取值,刨除陷入局部極小值的情況,記錄20次成功計算的迭代次數。實驗結果如圖2所示:

從圖2可以得出,對于本文中所采取的數據而言,學習率較小時,迭代次數較多;隨著學習率的增加,迭代次數減少。學習率取0．55時,迭代次數已經基本接近最小值。而當學習率取0．7以及0．85時,迭代次數并沒有顯著增加。但是當學習率取0．7以及0．85時, BP神經網絡的陷入局部極小值以及發生震蕩的次數明顯增加。因此,對于本文中的樣本數據,在后面的計算中,作者采用的學習率為0．55。

3．3算法的收斂速度比較

在本節中,作者采用算法的計算耗時作為評價算法收斂速度的指標。根據前面實驗結果,學習率選取為0．55。根據樣本數據計算時的收斂情況,動量系數取0．05。通過程序中內置的計時模塊,輸出每次計算的耗時,時間均四舍五入后取整到秒。使用的計算機為Dell M4800,處理器為i7-4810MQ,頻率為2．80 GHZ,內存為8 G。作者分別進行了20次實驗,計算結果如表2所示:

兩種算法的耗時(單位/s)　表2

將表2以折線圖的形式表示,如圖3所示:

從圖3可以看出,標準BP算法比附加動量算法的收斂速度快。但是在程序的實際計算過程中,標準BP算法陷入局部極小值的可能性很大,影響了算法的實用性。附加動量法相比標準BP算法,雖然收斂速度慢,但是避免了陷入局部極小值的情況,算法實用性更強。

圖3　兩種算法的收斂速度比較

3．4算法的穩定性比較

算法的穩定性是對每次計算耗時差異的量化指標。若算法每次計算的耗時差異較大,則這種算法的穩定性不高。否則,算法的穩定性就高。

在本節中,算法的穩定性使用下式計算:

上式中,N為計算的次數,XI是每次計算的耗時,為20次計算的平均耗時。根據表2中的實驗數據,計算兩種算法的穩定性。結果如表3所示:

兩種算法的穩定性　表3

由表3可知,標準BP神經網絡算法每次計算的耗時差異較小,算法穩定性較強。而附加動量法穩定性較差。但是,附加動量法避免了陷入局部極小的可能。

3．5算法的預測精度比較

利用本文采用的訓練樣本數據對預測樣本數據進行預測。利用預測樣本的殘差的平方和來評價算法的預測精度。實驗結果如表4所示:

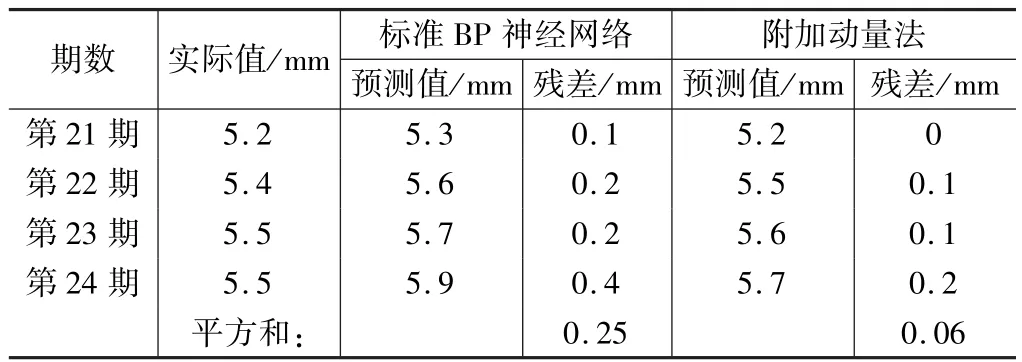
兩種算法的預測精度比較　表4

根據表格中的統計數據,用折線圖的形式表達,如圖4所示:

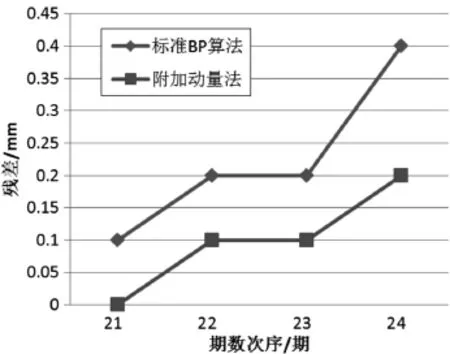
圖4　兩種算法的預測精度比較

表4中的預測值均取20次實驗的結果得平均值。我們可以看出,標準BP算法預測值殘差的平方和為0．25 mm2,附加動量法為0．06 mm2,附加動量法的預測精度優于標準BP算法。因此,對于本文采用的樣本數據而言,附加動量法的預測精度更好一些。

4　結 語

(1)對于本文采用的樣本數據而言,學習率較小時,BP神經網絡的迭代次數較多;隨著學習率的增加,迭代次數減少。學習率取0．55時,迭代次數已經基本接近最小值。而當學習率取0．7以及0．85時,迭代次數并沒有顯著增加。但是當學習率取0．7以及0．85時,BP神經網絡的陷入局部極小值以及發生震蕩的次數明顯增加。

(2)標準BP算法比附加動量算法的收斂速度快。但算法陷入局部極小值的可能性很大,影響了算法的實用性。附加動量的BP算法收斂速度慢,但是避免了陷入局部極小值的情況。

(3)標準BP算法每次計算的耗時差異較小,算法穩定性較強。而附加動量法穩定性較差,但避免了陷入局部極小的可能。

(4)對于本文采用的訓練樣本而言,附加動量法的預測精度優于標準BP算法。

[1] Berman O,Krass D,Drezner Z,The Gradual Covering Decay Location Problem on a Network[J]．European Journal of Operational Research,2003,151(3):474～480．

[2] 高穎,張雙杰,王麗娟等．對改進的自適應BP算法中參數研究[J]．合肥工業大學學報·自然科學版,2006,29(3):281～299．

[3] 黃世震,林淑玲．基于GSA-BP神經網絡的壓力傳感器溫度補償[J]．電子器件,2013,36(5):680～684．

[4] 候福均,吳祈宗．基于遺傳算法和模擬退火算法優化神經網絡的鐵路營業里程預測[J]．北京理工大學學報, 2004,24(3):247～250．

[5] Ding Shifei,Su Chunyang．An Optimizing BP Neural Network Algorithm Based on Genetic Algorithm[J]．Spring, 011,36:153～162．

[6] 王英,曹軍,孫麗萍．基于SAGA優化BP神經網絡的木材含水率預測[J]．控制理論與應用,2013,32(1):4～13．

[7] 董鵬,羅朝暉,伍潔等．BP神經網絡的遺傳模擬退火算法動態選址仿真[J]．火力與指揮控制,2012,37(12):27～30．

Research on Application of Standard BP Neural Network Algorithm and Back-propagation With Momentum in the Practice of Engineering Settlement Monitoring

Li Bo1,Liu Huaqiao2,Dai Xin3,Jia Zhiqiang4

(Tianjin Institude of Surveying and Mapping,Tianjin 300381,China)

In the practice of engineering settlement monitoring,according to the difference of forecast methods and characteristics of the settlement trend,the accuracy of the prediction results will be different．With the deepening application,improving available algorithms to make the advantages of each algorithm a difference,has become the mainstream of research．In this paper,author implemented the standard BP neural network algorithm and back-propagation with momentum．By researching the effect of different learning rates for the standard BP neural network algorithm to determine the size of the learning rate．Then,author studied the effect of momentum on convergence speed of back-propagation with momentum,to determine the value of momentum．Finally,comparing the stability and efficiency of algorithms and forecast accuracy to explore the characteristics of the two algorithms．

settlement monitoring;BP neural network;back-propagation with momentum

1672-8262(2016)01-145-04

P258

B

?2015—12—07

李波(1989—),男,碩士,助理工程師,主要從事工程測量等技術工作。