基于狄洛尼三角網的等高線及挖填方分析研究

周浩,蔡歡

(天津市測繪院,天津 300381)

基于狄洛尼三角網的等高線及挖填方分析研究

周浩?,蔡歡

(天津市測繪院,天津 300381)

基于對外業測量數據三維表達的目的,采用改進的逐點插入法構建狄洛尼(Delaunay)三角網,并結合Auto-CAD Civil 3D進行測量數據三維展示,實現了三維環境中等高線的繪制以及挖填方土方量的計算,可以較好擬合地形等高線起伏,直觀分析挖填方的位置和土方量,使AutoCAD的應用由傳統的二維模式向三維模式轉變。

狄洛尼三角網;等高線;土方計算

1　引 言

數字地形模型(DTM)是對地表形態及屬性信息的數學表達,包含空間坐標屬性及地形屬性特征。當其地形屬性為高程值時,又被稱為數字高程模型(DEM)。DTM主要有三種模型:等高線模型、規則格網模型和不規則三角網模型。等高線模型能比較直接地反映地形地貌,但不適合進行坡度計算、挖填方計算等地學計算。規則格網模型在GIS應用中很有利,但其數據量大,且需要分布較為規則的高程點數據的特點,難以表達復雜地形地貌。在大比例尺地形圖的生產中,傳統野外測量方法獲取到的高程信息大多是不規則的離散點,一般采用不規則三角網(TIN)來表示其地形地貌變化[1]。在所有三角網生成方法中,狄洛尼三角剖分不僅能保證三角網的唯一性,而且能盡可能地避免狹長三角形的出現,是生成TIN的最好方法。

狄洛尼三角網具有以下三個性質:

(1)空外接圓性質:三角網中每個三角形的外接圓都不包含點集中的其余點。

(2)最大最小角度性質:在所有可能生成的三角網中,各三角形最小角之和最大。

(3)唯一性:無論從何點開始構造三角網,最終生成的狄洛尼三角網相同。

2　逐點插入法構造狄洛尼三角網

2．1狄洛尼三角網生成算法

狄洛尼三角網生成算法主要包括三類:逐點插入算法、三角網生長算法、分割合并算法。經試驗發現:分割合并算法對復雜分布的離散點處理效果不理想,當相鄰子三角網的形狀都很不規則時,合并后的三角網極有可能出現不合理的凹陷部分。三角網生長算法則需要對每個新生成的三角形的三條邊分別進行循環擴展,同時剔除重復三角形,直到沒有新的三角形生成[2]。該方法算法簡單,但是算法效率極低。所以本文采用改進后的逐點插入法來生成狄洛尼三角網,其算法思想是:

(1)剔除重復點。

(2)生成一個包含所有離散點的超級三角形。

(3)循環點集中的每個點:求出當前離散點落在哪些已有三角形的外接圓內,獲取在這些三角形中只出現過一次的邊,將這些邊與當前點組成新的三角形,并刪除受影響的三角形。

(4)將包含超級三角形頂點的三角形刪除。

2．2三角形類

三角形類的主要作用包括:存儲該三角形的三個頂點坐標;判斷一個點是否是該三角形頂點;計算三角形面積、重心、外接圓圓心及半徑。

2．3三角形邊類

三角形邊類的主要作用是存儲邊的兩個頂點以及判斷兩條邊是否重合。

3　狄洛尼三角網的應用

傳統的二維平面對地形地貌的表現能力不足,體現為美觀性和易讀性較差。不規則三角網模型(TIN)的結構邏輯性強,數據量適中,利于進行坡度、坡向分析以及挖填方等地學計算。因此本文采用AutoCAD Civil 3D作為底層平臺,實現基于狄洛尼三角網的等高線繪制和挖填方計算兩個方面的應用。

3．1繪制等高線

等高線用來展示地形地貌特征。在三角網中通過內插方式生成等高線,以三維的方式繪制地表等高線分布,可以直觀的表現地面的起伏狀況,流程如下:

(1)遍歷三角網中的每一個三角形,根據當前高程CurElev和三角形頂點坐標,計算三角形三邊上的等值點。如果該三角形邊上等值點的數量大于1個,則將這些等值點放入一個點集合CurPoints,再將這個點集合放入點集合鏈表AllPoints中。

(2)如果AllPoints中點集合總數大于0,則從All-Points中取出第一個點集合,作為新等高線的點集合LinePoints,否則退出。

(3)遍歷AllPoints中的點集合,將點集合中的點和LinePoints中的第一個點或最后一個點做比較。如果相等,則將點集合中的其他點加入LinePoints頭部或者尾部,并將點集合從AllPoints中移除。

(4)當AllPoints點集合中的所有點都不與Line-Points中第一個點或最后一個點相等時,表明當前等高線已經生成完畢。返回執行第2步直至AllPoints遍歷完畢。

(5)利用AutoCAD Civil 3D將LinePoints點集合進行繪制,生成三維等高線圖,如圖1所示。

圖1　三維等高線圖

3．2DTM法挖填方計算

在建設施工項目中土方量計算是一項十分重要工作,關系到項目各方的切身利益。區域內挖填方的計算方法包括等高線法、DTM法、斷面法以及方格網法,每種方法有不同的使用范圍[3]。DTM法挖填方計算的原理是三角棱柱體積法,通過計算范圍線內每個三角形區域的挖填方量,最終得到整個區域的挖填方總量[4]。計算流程如下:

(1)根據高程點集和選取的閉合范圍線,得到計算區域的三角網。通過構造狄洛尼三角網得出需要計算的三角形。

(2)計算每個三角形的挖填方量。根據三角形挖填高度的不同,其挖填方計算方式分為兩種:全挖或全填或有挖有填。

3．2．1全挖/全填

此時挖填部分是一個標準的三角棱柱體,如圖2所示,其體積計算公式:

式中:S為三角形在XY平面上的投影面積,利用海倫公式計算;H1、H2、H3是三角形各頂點的挖填高度(取絕對值)。3．2．2 有挖有填

圖2　全挖或全填

零線將三角形分成兩個部分,根據零線與三角形的相交關系,存在兩種分割情況:①零線經過三角線的一個頂點,與對邊相交,形成兩個底面為三角形的錐體;②零線與三角形兩條邊內部相交,分別計算錐體和楔體的體積。零線與三角形兩條邊內部相交,形成一個底面為三角形的錐體和一個底面為四邊形的楔體。

①零線經過三角形的一個頂點,形成的兩個底面為三角形的錐體,可以看做是兩個三棱錐,如圖3所示,其體積計算公式:

式中:S是錐體在XY平面的投影面積;H3是錐體頂點的挖填高度(取絕對值)。

錐體部分的體積計算公式:

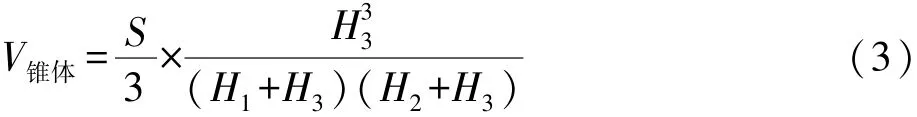
式中:S為三角形在XY平面的投影面積;H1、H2、H3為三角形各頂點的挖填高度(取絕對值),其中H3為錐體頂點的挖填高度,如圖4所示。

楔體部分的體積計算公式:

圖4　錐體和楔

利用AutoCAD Civil 3D搭建操作視圖窗口,支持不同數據來源的原始地形數據和設計面數據,數據計算入口界面和計算結果顯示界面分別如圖5、圖6所示:

圖5　土方計算數據入口

圖6　土方計算結果

4　結 論

利用改進后的逐點插入法生成狄洛尼三角網,并結合具有三維顯示引擎的AutoCAD Civil 3D,對外業測量數據進行三維展示,通過等高線構成算法和DTM挖填方算法,實現三維環境中的等高線生成和土方量計算,以可旋轉、可漫游的方式對數據進行立體展示,從而更真實地表達外業實測地貌形狀,更直觀地分析挖方、填方的剖面構成,更準確地計算挖填方土方量。

[1] 劉永和,王燕萍,齊永安．一種簡單快速的Delaunay三角網逐塊生成算法[J]．測繪科學,2008(6):133～135．

[2] 許麗敏,薛安．基于Delaunay三角網與Voronoi圖聯合提取等高線骨架的地形重建算法研究[J]．北京大學學報, 2009(4):647～652．

[3] 林偉明,林青海．南方CASS成圖軟件中三角網對工程量計算的探討[J]．四川水力發電,2012(6):92～94．

[4] 關金華,趙遠方,胡金陽等．基于TIN的工程土方量計算[J]．礦山測量,2011(6):69～72．

[5] 徐朱,方強,翟輝．基于TIN的土石方計算研究[J]．江蘇科技信息,2014(13):39～41．

The Analysis of Contour and Earthwork Calculation Based on Delaunay Triangulation

Zhou Hao,Cai Huan

(Tianjin Institute of Surveying and Mapping,Tianjin 300381,China)

For the purposes of displaying External measurement data in three-dimensional model,the author used the improved method of inserting point by point to build the Delaunay triangulation,combined with AutoCAD Civil 3D,so it can draw contours and calculate the cut and fill earthwork square in three dimensional environment,this can better fit the terrain contour movements,can visually analyze the location and earthwork of excavation and filling side,in short,it changes the use of AutoCAD applications from the traditional two-dimensional model to three-dimensional model．

delaunay triangulation;contour;earthwork calculation

1672-8262(2016)01-110-04

P208．1,P209

B

?2015—12—23

周浩(1988—),男,工程師,研究方向:地理信息系統。

天津市國土資源和房屋管理局科研項目(津國土房科驗字[2015]第022號)