基于三種重力場模型在區域大地水準面中的應用

張國清,譚文輝,賈旸

基于三種重力場模型在區域大地水準面中的應用

張國清?,譚文輝,賈旸

在傳統大地水準面精化中,因高精度、高分辨率的DEM數據與重力異常數據獲取困難,從而無法顧及地形及重力數據對大地水準面的影響,導致大地水準面的精度無法滿足要求。針對上述問題,本文探討了利用SRTM地形數據代替所需的高精度、高分辨率DEM地形數據,在我國數據空白區域,試驗了不同分辨率的SRTM地形數據對區域大地水準面精化的影響,并在SRTM數據基礎上顧及EGM96、EGM2008、Eigen-5C三種地球重力場模型,完成小區域大地水準面精化的實驗,分析了大地水準面受SRTM數據影響的程度和規律。

大地水準面;重力場模型;SRTM;地形影響

1　引 言

國內外許多文獻都研究過試圖在無重力數據、無地形數據的地區,通過運用連續的數學曲面模型、基于地球重力場模型的“移去——恢復”方法或是基于地形改正的擬合方法來精化大地水準面,試驗結果表明上述方法在平原地區能得出滿意的結果,但在山區、丘陵、高原地區大地水準面精度卻不能滿足要求。主要原因體現在前兩種方法僅顧及到大地水準面差距的中長波分量,而忽略了受地形與重力影響的短波分量;而后一種方法雖顧及到受地形影響的短波分量,但在全國多數地區因缺乏高精度、高分辨率的DEM地形數據,從而得不到推廣[1]。目前為了顧及大地水準面精化中地形與重力數據對高程異常中的影響,通常利用組合法1(GPS/水準+地球重力場模型+地形DEM)和組合法2(GPS/水準+地球重力場模型+地形DEM+地面重力異常)計算大地水準面差距或高程異常的精確值[2]。但針對我國多數地區地形數據較少且分布很不均勻的現狀,本文旨在無地形數據的區域利用航天飛機雷達地形測繪數據(SRTM)代替大地水準面精化中所需的DEM數據,分析SRTM地形數據對精化大地水準面所產生的影響。

本文主要考察在區域大地水準面精化范圍內應用SRTM數據代替該地區實際的DEM數據,主要是考慮到:首先SRTM數據本身帶有誤差,對范圍較大的大地水準面精化中帶入何種誤差暫不明確,其次是范圍適中的區域內,大地水準面差距的變化比較平滑,地形所引起的短波影響相對更突出,方便對比。文中首先介紹了兩種高程異常的分解方式;其次,基于實例把顧及SRTM數據的兩種方法精化結果進行對比,得出一些有意義的結論。

2　地形起伏影響的數學模型及實驗方法

大地水準面精化中顧及地形影響的短波分量影響的關鍵是把高程異常分解為較為光滑的中長波項和局部地形起伏引起的短波項組成[2,3]:

式中,ξ0為高程異常的中長波項;ξTC為高程異常的短波項。第二項由地形起伏引起的,故在平坦地區, ξTC較小;而在山區地帶,ξTC影響較大。

基于該理論,如果能求解ξTC,并在ξ中將ξTC扣除,則可近似認為ξ0=ξ-ξTC為較為光滑的幾何曲面,再利用測區中已知GPS水準點確定一個ξ0的曲面函數,再次利用該模型確定其他待求點的ξ0值。利用式(1)便可以求得ξ。該方法也就是地形起伏的影響“移去—恢復”的過程。

設測區有一參考面Hr,則高出或者低于Hr的地形對P點的引力位為

式中,G為萬有引力常數;ρ為地球平均質量密度, H為數字地面模型格網點高程;Hr參考面高程。

由地形起伏引起的高程異常ξT為:

式中,γ為計算點的正常重力值。

為了便于積分運算,對式(2)展開:

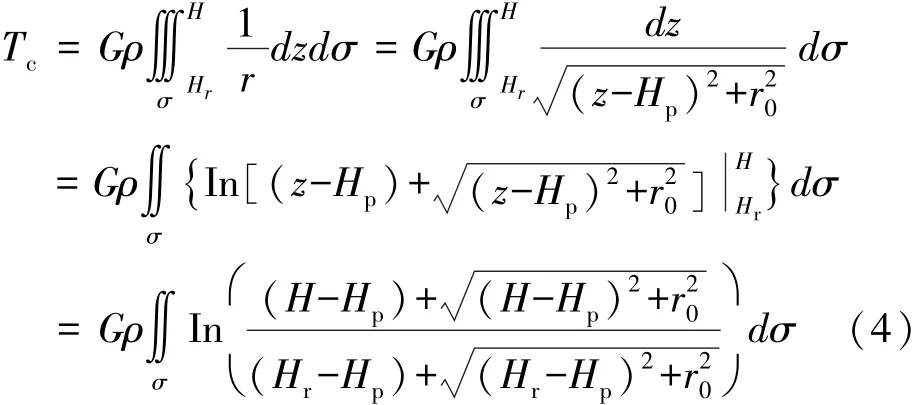
為了便于研究SRTM數據的可靠性,本文中把高程異常值按兩種不同的方式進行分解:

(1)ξ=ξ0+ξTC,ξ0為高程異常的中長波項,ξTC為因地形起伏影響所致的高程異常短波項。

(2)ξ=ξGM+ξTC+ξr,ξGM為有地球重力場模型計算的大地水準面差距,ξTC為地形起伏影響的短波項,ξr為殘差高程異常。其中方法1僅顧及了地形的影響,而方法2在方法1的基礎上顧及了EGM96, EGM2008,Eigen-5C三種地球重力場模型對高程異常中長波分量的影響。

3　算例計算及結果評估

文中實驗計算區域選擇遼寧省某地級市部分區域,該區域面積為3 550 km2,該區域的平均高程在105 m左右,地形起伏略大,主要以山地與平原為主,區域內共有15個GPS水準點,且15個GPS水準點的高程異常值基本都保持在慮8 m～12 m之間,變化稍大。此外從國際科學數據服務平臺上分別獲取該實驗區域分辨率為30″×30″、1′×1′的SRTM地形數據[4,5]。

3．1實驗思路

實驗思路按照第2節的兩種高程異常分解方法先分解,再分別計算各分量值:

(1)首先計算15個GPS水準點的地形改正值ξTC,利用已知點真實高程異常減去地形改正值得到高程異常的中長波項ξ0,由于除去地形改正后的高程異常的中長波項ξ0比較平滑,因此再以作為已知值,再利用神經網絡方法擬合未知點值[6]。

(2)首先計算15個GPS水準點的地形改正值ξTC;其次,利用三種地球重力場模型計算15個GPS水準點的模型大地水準面差距;最后,已知點真實高程異常減去地形改正值和模型大地水準面差距值ξGM,ξr往往比較平滑,再以其作為已知值,利用神經網絡等方法擬合未知點值[6]。

3．2地形影響值及各分量值計算

對15個GPS水準點地形影響值的計算,我們選擇利用該實驗區的1′和30″SRTM數據按照式(4)完成,計算時參考高程面選擇為該區域的平均高程面即109 m的高程面。

15個GPS水準點地形改正值ξTC和分解方法1中場波項ξ0的數據統計/m表1

表1為按照思路1計算GPS水準點的各部分分量,從地形改正值的統計結果分析:(1)實驗區的GPS水準點受地形影響較明顯,地形改正絕對值最大的能達到37 cm,最小的也有2．3 cm;(2)對比1′與30″DEM對15個GPS水準點的地形改正值,變化值最大僅為1．5 cm,變化最小值為4 mm。說明分辨率的變化對計算值的影響僅為厘米級。觀察GPS水準點剔除地形改正值過后1′和30″中長波項的結果,首先無論最大值或最小值都較已知高程異常值有所變化,變化區間都減小了;其次從標準標準偏差值來看,中長波項ξ0的偏差值較已知高程異常值要小的多,說明剔除地形改正值后的中長波項ξ0相對真實高程異常值要平滑的多。

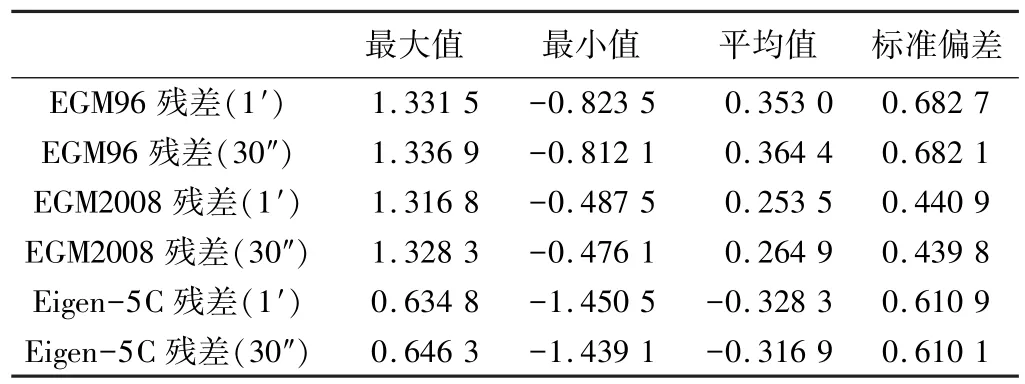
15個GPS水準點基于三種重力場模型的殘差高程異常值ξr的數據統計/m表2

表2為按照思路2基于EGM96、EGM2008、Eigen-5C三種地球重力場的殘差高程異常值的計算值,從統計結果分析:基于EGM2008模型的殘差值和標準偏差值較EGM96、Eigen-5C模型的殘差值和平均值要小很多,說明基于EGM2008模型的殘差值相對要平滑很多。

3．3“擬合—恢復”過程

“擬合—恢復”過程:即把平滑后的中長波項或者殘差值作為已知點數據,從中選取學習訓練樣本,運用BP神經網絡模型訓練,預測未知點的中長波項和殘差值,再逆向加上地形改正值和模型大地水準面差距值計算未知點高程異常,并與未知點的真實高程異常值比較,觀察擬合偏差值大小。

方案一:按思路1的模式分解高程異常,從統計的中長波項中選擇6個點作為學習樣本,其他9個點作為檢核數據。對15個GPS水準點的標準偏差值進行排序,均勻選擇不同階段偏差值的6個點作為學習樣本點。中間層設定為從6～26的偶數值,網絡目標為0．000 1。分別采用擬牛頓算法(trainbfg)、動量及自適應lr的梯度下降訓練法(traingdx)、Levenberg-Marquardt訓練法(trainlm)進行網絡訓練[7]。

從方案一的統計結果圖分析,僅顧及地形改正的GPS高程神經網絡擬合方法擬合精度不理想,從結果中分析,基于trainlm函數的擬合值要略高于traingdx函數和trainbfg函數的擬合值,平均能達到20 cm～30 cm的精度,而且根據9個未知點的擬合統計值如圖1,traindx函數的擬合與真實值最為接近;但其他兩種函數的擬合精度要略低些,在個別點擬合誤差較大。

圖1　方案1中基于神經網絡3類函數的高程異常擬合值

方案二:按思路2的模式分解高程異常,從統計的殘差高程異常中選擇6個點作為學習樣本,其他9個點作為檢核數據。學習樣本點的選擇方法也采用均勻選取方法。中間層設定為從6～26的偶數值,網絡目標為0．000 1。分別采用擬牛頓算法(trainbfg)、動量及自適應lr的梯度下降訓練法(traingdx)、Levenberg-Marquardt訓練法(trainlm)進行網絡訓練[7]。

圖2　方案2中基于EGM96模型神經網絡3類函數的高程異常擬合值

圖3　方案2中基于EGM2008模型神經網絡3類函數的高程異常擬合值

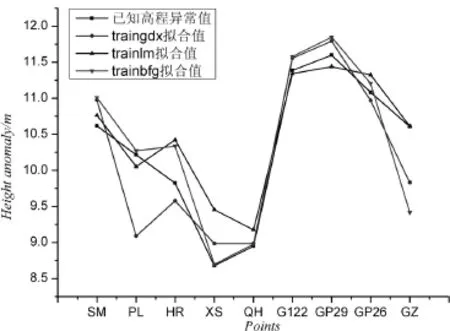
圖4　方案2中基于Eigen-5C模型神經網絡3類函數的高程異常擬合值

根據方案2基于3種地球重力場模型的實驗計算結果對比方案1,從整體觀察,方案2的擬合效果要明顯好于方案1?；贓GM96和EGM2008模型的三種函數的擬合精度大致相當,都能15 cm左右,而基于Eigeng-5C模型的三類函數的擬合值精度要低,平均在15 cm～20 cm左右。這說明融合重力場模型和地形改正的高程異常擬合方法比僅融合地形改正的高程異常擬合方法要好,主要原因是針對鞍山實驗區,由于地形起伏變化略大,重力場信息和地形起伏信息一樣對大地水準面差距和高程異常的求解都有著很重要的影響,不能忽視?；贓GM96、EGM2008、Eigen5-C三種模型平均的精度差分別能達到10 cm、6 cm、10 cm～15 cm;而且兩類比較結果說明,在實驗區, EGM2008重力場模型比其他兩種模型擬合精度更高,更適合實驗區的工程需要[8]。

4　總 結

在區域大地水準面精化實驗中,用SRTM數據代替實驗區域高精度的DEM,并剔除地形影響所致的短波項,能有效的改變高程異常的平滑度。方法1中把高程異常分解成中長波項和地形影響短波項,剔除短波項過后,中長波項雖然比已知高程異常原始值要平滑,檢核點的擬合精度卻偏大,只能達到20 cm左右。方法2中把高程異常值分解成模型大地水準面差距和地形影響短波項,最終檢核點的擬合精度較僅顧及地形改正項的實驗結果要好,而且基于EGM2008模型的擬合結果最優。實驗結果證實了EGM2008模型的精度較高,而且在山地、丘陵等地勢較復雜地區,考慮地球重力場模型計算的中長波項能取得更好的結果。

[1] 趙建虎,劉經南．顧及非格網數據考慮地形改正的GPS水準高程擬合[J]．武漢測繪科技大學學報,1999,24 (4):346～350．

[2] 羅志才,陳永奇,寧津生．地形對確定高精度局部大地水準面的影響[J]．武漢大學學報,2003,28(3):340～344．

[3] 張同剛,岑敏儀,馮義從等．地形起伏對GPS工程控制網高程異常的影響[J]．鐵道學報,2005,27(1):79～83．

[4] Yang Z J,Chen Y Q．Determination of the Hong Kong Gravimetric Geoid[J]．Survey Review,2001,36(279):27～34．

[5] Corchete V,Chourak M,Khattach D．The high-resolution Gravimetric Geoid of Lberia:IGG2005[J]．Geophysical Journal International．2005,162:676～684．

[6] 林淼,朱建軍,楊經豪等．地球重力位模型確定局部大地水準面起伏的比較研究[J]．武漢大學學報·信息科學版,2009,34(10):1194～1198．

[7] 閻平凡,張長水．人工神經網絡與模擬進化計算[M]．北京:清華大學出版社,2000,5～6．

[8] 羅佳,施闖,鄒賢才等．現有SST重力場模型的比較研究[J]．武漢大學學報·信息科學版,2006,31(7):594～595．

(貴陽市測繪院,貴州貴陽 550002)

Application of Regional Geoid Based on Three Types Gravity Field Model

Zhang Guoqing,Tan Wenhui,Jia Yang
(Guiyang Surveying and Mapping Institute,Guiyang 550002,China)

During traditional geoid refining,considering the difficult of the many areas that have not enough highprecision and high-resolution DEM and gravity anomaly,so the precision of geoid can’t meet the requrirement．Aiming at the above problems,this thesis using SRTM in instead of required high-precision and high-resolution DEM,having tested relevance with different DEM resolution in data blank areas,then have completing the experiment of regional geoid with EGM96、EGM2008、Eigen-5C,and have analysising the law of geoid based on SRTM．Some conclusions of this paper are very significant to study influence of GPS height transformation and geoid refining which areas without data．

geoid;gravity fieid model;SRTM;topographic effect

1672-8262(2016)01-16-04

P223

A

?2015—12—07

張國清(1985—),男,碩士,助理工程師,研究方向:大地水準面精化。