計及LVRT撬棒電路的雙饋感應風電機組動態等值

朱婷涵，李生虎，馬燕如，鮑正杰

（合肥工業大學電氣與自動化工程學院，合肥 230009）

計及LVRT撬棒電路的雙饋感應風電機組動態等值

朱婷涵，李生虎，馬燕如，鮑正杰

（合肥工業大學電氣與自動化工程學院，合肥 230009）

低電壓穿越LVRT（low-voltage ride-through）的同時電機結構發生變化，機組差異使撬棒動作不一致，給傳統等值方法帶來難度，且效果不佳。考慮到風電場對大電網的影響主要關注其出口動態特性，為改善計及LVRT時風電場的等值效果，從其出口特性著手，忽略內部結構，等效整個風電場。通過Prony算法分析風電場出口電壓、電流的振蕩模式，定義表征各模式影響程度的能量比，以此為依據提取主要模式等效風電場出口特性，并與依據模式的幅值和衰減因子提取的主要模式對比，前者提取的主要模式更為精確，且減小了對模型階數的要求。仿真結果表明該算法得到的等值模型在計及LVRT時是合理有效的。

雙饋感應電機；動態等值；Prony算法；低電壓穿越；振蕩模式；能量比；出口特性

隨著大規模風電接入電網，風力發電對電力系統安全穩定運行的影響日益顯著[1-4]。動態仿真時如果對每臺風力發電機都進行詳細建模，整個風電場將是一個高階模型，計算速度和內存壓力將很大。因此，風力發電機動態等值建模的迫切性日益凸顯[5-8]。

目前，風電場的等值方法主要有：容量加權等值[5]、優化算法等值[6-7]、在線系統辨識[8-9]等。文獻[10]依據尾流效應影響對風電場進行區域劃分，將風力發電機組合并簡化，建立風電場整體簡化模型；文獻[11]基于跌落電壓下定子瞬時電流的數學表達方式，提出了一種基于最小二乘法的雙饋感應電機參數辨識方法；文獻[12]通過各參數的軌跡靈敏度和相位判斷其可辨性，并設計了基于蟻群算法的雙饋感應電機參數辨識方法。

電網發生故障時，撬棒投入前后雙饋感應電機DFIG（doubly-fed induction generator）結構發生變化[13-15]。文獻[10]考慮了風速的影響，但忽略了機組間其他差異對撬棒動作的影響，此時按尾流效應劃分，會影響等值精度；文獻[11]適用于單臺DFIG，對于多臺電機，由于網側變流器無功補償電流的影響，并且電機結構變化不同步，不宜用類似的數學表達式表示出口電流；文獻[12]不需要具體數學表達式，等值結果不受撬棒動作的影響，但蟻群算法依賴參數的設置，收斂速度慢且容易陷入局部最優，因此其等值精度會受到蟻群算法的制約。上述等值算法都側重于風電場內部參數的等值，考慮低電壓穿越LVRT（low-voltage ride-through）時精確等值風電場內部參數有較大的難度，而分析風電場特性時，往往關注的是其對外部電網的影響。

Prony算法是一種常用的信號處理方法，可以直接得到采樣數據的振蕩特性，相比頻域響應方法計算量大為減少，近年來在電力系統中得到了廣泛應用[16]。文獻[17]利用Prony算法分析傳遞函數的留數和特征根，設計PSS（power system stabilizer）參數；文獻[18]用于分析電力系統的低頻振蕩模式，研究系統穩定性；文獻[19]將其應用于電力系統模型的辨識。

本文將Prony算法用于風電場外部特性等值，提取出口電壓、電流的主要振蕩模式，將其線性組合，擬合風電場出口電壓、電流，并建立節點模型，等效整個風電場。根據幅值和衰減因子、模式的能量比，分別提取主要模式。前者計算量小、速度快，但該方法有一定主觀性，可能遺漏較為重要的模式；后者能直觀地反映各模式的重要程度，設置能量閾值確定主要模式數，濾除Prony階數選擇不準確引入的雜散模式。同時，劃分等值區間盡可能減小每個區間外界對系統的影響。

1 Prony算法介紹

1.1 Prony算法

Prony算法用一組指數項的線性組合來擬合采樣數據，從而得到信號幅值Ai、頻率fi、衰減因子σi和初相角ψi等信息。對于測量數據y（1），y（2），…，y（N），其擬合表達式為

式中：p為擬合模型的階數；Bi、Zi為包含信號振蕩特征的復數，表示為

式中：Δt為采樣時間間隔。

Prony算法通過最小二乘法估算信號各模式的振蕩特征，令誤差平方和最小，得到Ai、ψi、σi、fi等參數。誤差平方和表達式為

定義信噪比SNR（signal noise ratio）檢驗Prony算法擬合效果，SNR越大誤差越小。

SNR的計算公式為

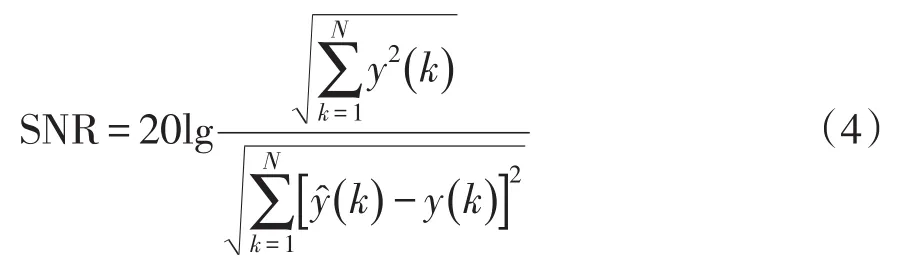
1.2 電力系統模型的特點

電力系統的模型可以用一般形式的微分-代數方程組表示，即

式中：x為微分方程組中描述系統動態特性的狀態變量；y為代數方程組中系統運行參量。

系統線性化模型為

式中：矩陣A、B、C、D為包含函數f和g關于狀態變量x和輸入量y的偏導數。

將式（6）做Laplace變換，整理得

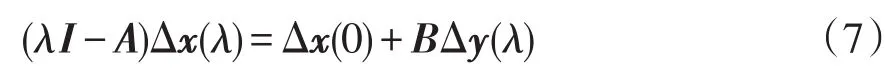
式中：x（0）為狀態變量初值；λi為矩陣A的第i個特征值，可以表示為

特征值反映了系統動態特性，而這部分信息已經包含在Prony算法表達式的Zi中。電力系統是一個非線性的動態模型，Prony算法通過線性方程組求解非線性問題，因此利用Prony算法將系統輸出的信號分解為指數項的組合，可以得到系統的動態特性。

2 計及LVRT風電場出口特性等值

風電場出口故障時，為了保持風電機組并網運行，轉子側并聯撬棒電路是電網故障時DFIG常用的低電壓穿越措施，此時DFIG以異步電機的狀態運行。

低電壓穿越過程中，風電場中各機組撬棒不同步投切，導致風電場中同時存在雙饋感應電機和異步電機，等值風電場內部電機參數難度較大。其次，分析風電場對電力系統影響，關注的是其出口動態特性。因此，可以忽略風電場內部的具體結構，將其整體等值為系統的一個節點，只關注其出口電壓和電流的動態特性。

Prony算法分析風電場出口電壓和電流的振蕩模式，從中選擇主要振蕩模式，將其線性組合，得到電壓、電流動態過程的數學表達式，表示整個風電場出口特性，為風電場并網、保護整定等提供依據。

2.1 采樣區間的劃分

Prony算法要求在采樣區間內的系統是一個不受外界影響的自由振蕩系統，從而得到各模式的振蕩特性。

低電壓故障過程中，風電場中由于各臺機組間的差異，撬棒動作特性不同。若不劃分區間，則擬合的振蕩特性必然受撬棒投切的影響，出現較大誤差。因此在利用Prony算法進行振蕩模式分析前，需要對采樣數據劃分區間。

故障起始/結束、撬棒投入/切出是仿真過程中的擾動點，依據這幾個點對采樣區間進行劃分，盡可能保證在該段采樣區間振蕩模式的一致性，分段進行Prony分析。考慮到時間間隔太短、采樣點過少不利于振蕩模式的分析，以每個采樣區間內采樣點不少于20為其劃分依據。

2.2 基于幅值、衰減因子的主要振蕩模式選擇

通過Prony算法分析參數的振蕩模式，模式的幅值決定模式起始振蕩的幅度，衰減因子決定模式衰減至0的快慢，它們是影響振蕩的關鍵因素。若模式i的幅值|Ai|相較采樣起始點幅值|A0|很小，即使其衰減因子絕對值|σi|很小，由于起始振蕩幅度太小，對于擬合參數影響不大；衰減因子絕對值|σi|很大時，相對于參數整體而言，該模式很快就衰減為0，因此|σi|很大的模式對擬合參數影響不大。本文設定若模式i的Ai和σi同時滿足判據

判據1 |Ai|≥0.05|A0|

判據2 |σi|≤min（|σ1|，|σ2|，…，|σp|）+10

則將模式i視為主要振蕩模式。

2.3 基于能量比的主要振蕩模式選擇

Prony算法可以將風電場LVRT過程中出口電壓、電流分解為多個指數項的線性組合，每個指數項代表一種振蕩模式，定義第i個振蕩模式的能量Ei為該指數項與x軸包圍區域的面積，則有

各模式對應的能量一定程度上反映了該模式對采樣信號的影響，定義能量比ξi表征其影響程度，表達式為

模型階數的準確選擇較難，即使能掌握系統的準確階數，當模型中存在相同模態時，也會由于存在項的合并導致階數選擇不準確。通過Prony分解得到的振蕩模式中往往存在雜散模式，這些雜散模式對于擬合風電場出口電流、電壓沒有意義。此外部分模式對電壓、電流特性的影響較小，用所有模式的組合表示動態特性，導致模型過于復雜，而等值效果的改善作用并不明顯。

本文通過設定能量閾值選擇對信號的組成有較大影響的模式，即主要振蕩模式，從而實現較少的模式組合等值風電場動態特性。能量閾值的設定取決于對等值模型精度的要求，同時兼顧等值模型的表達式復雜程度，本文設定能量閾值ζ為0.98，通過仿真驗證，其能較好地兼顧上述要求。此外，從能量的角度選取主要振蕩模式減小了對于模型階數p準確性的要求。

對于第K個采樣區間主要振蕩模式選擇的流程如圖1所示。選擇能量比較大的hK個振蕩模式線性組合并轉換為連續函數，即可得到等值風電場電壓或電流，即

式中：m為區間數；hK為區間K的主要模式數；TSK、TEK分別為區間K的起點、終點。

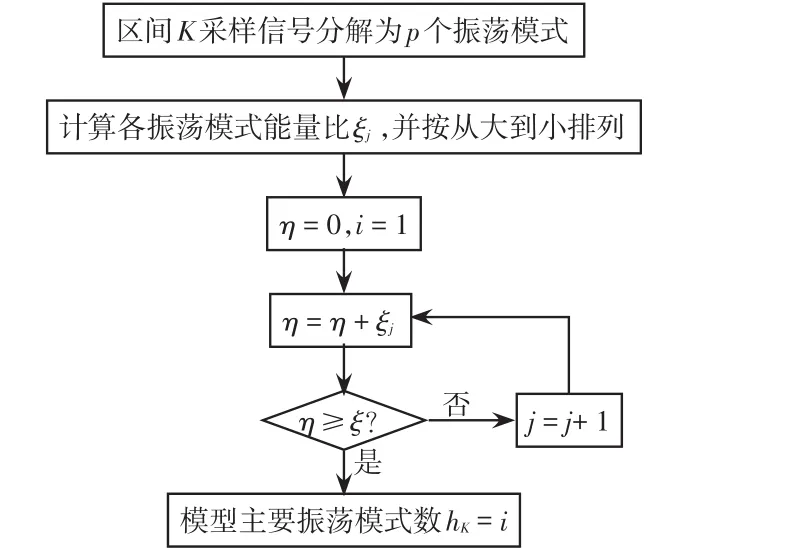
圖1 主要振蕩模式選擇流程Fig.1 Process of major oscillation mode selection

2.4 誤差定義

定義平均相對誤差d考察擬合值總體可信度，即

式中：xi、xit分別為等值前后的觀測量。

定義均方根誤差RMSE（root mean square error）衡量等值前后偏差，即

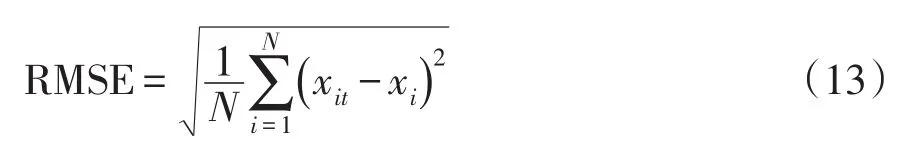
3 算例仿真

算例采用新英格蘭測試系統。風電場由1.5 MW和2 MW兩種型號DFIG各15臺組成。將風電場接入39節點測試系統中節點21，如圖2所示。在1 s時線路22-23發生三相短路，故障持續0.1 s，轉子電流Ir≥2.0 p.u.時撬棒投入，轉子電流Ir≤0.35 p.u.時撬棒切出。

圖2 含風電場的新英格蘭39節點系統Fig.2 New England 39-node system with wind farm

3.1 Prony采樣區間劃分

為研究采樣區間劃分對模型擬合精度的影響，采用不同的區間劃分方案如表1所示。方案1按故障前、故障中、故障后劃分；方案2在方案1的基礎上按撬棒切除時間細化區間。采樣時間間隔Δt= 0.005 s，風電場出口電流IG等值效果如圖3所示，等值誤差如表2所示。

由此可見方案2等值效果優于方案1，這是由于方案1的區間3中包含撬棒相繼切除的過程，系統振蕩模式發生變化，等值誤差較大，方案2通過細化采樣區間減小誤差。根據系統振蕩模式改變的時間點劃分區間能獲得更好的等值效果。

表1 區間劃分Tab.1 Division of section

圖3 不同區間劃分方案出口電流IG等值效果Fig.3 Equivalence effects on IGwith different ways of section division

表2 不同方案等值誤差Tab.2 Equivalence errors of different ways

3.2 基于能量比的主要振蕩模式選擇

選取1.525～3.000 s的風電場出口電流IG，該時間段內機組撬棒已經切除，驗證基于能量比的主要振蕩模式選擇方法可行性。

選取階數p為25和98，得到各振蕩模式的能量比如圖4所示。

圖4 各振蕩模式能量比Fig.4 Energy ratios in different oscillation modes

設定能量閾值0.98，選擇的主要振蕩模式如表3、表4所示。等值效果如圖5所示，誤差如表5所示。

表3 p=25時IG主要模式的振蕩特征參數Tab.3 Characteristic parameters of IGin major oscillation mode when p=25

表4 p=98時IG主要模式的振蕩特征參數Tab.4 Characteristic parameters of IGin major oscillation mode when p=98

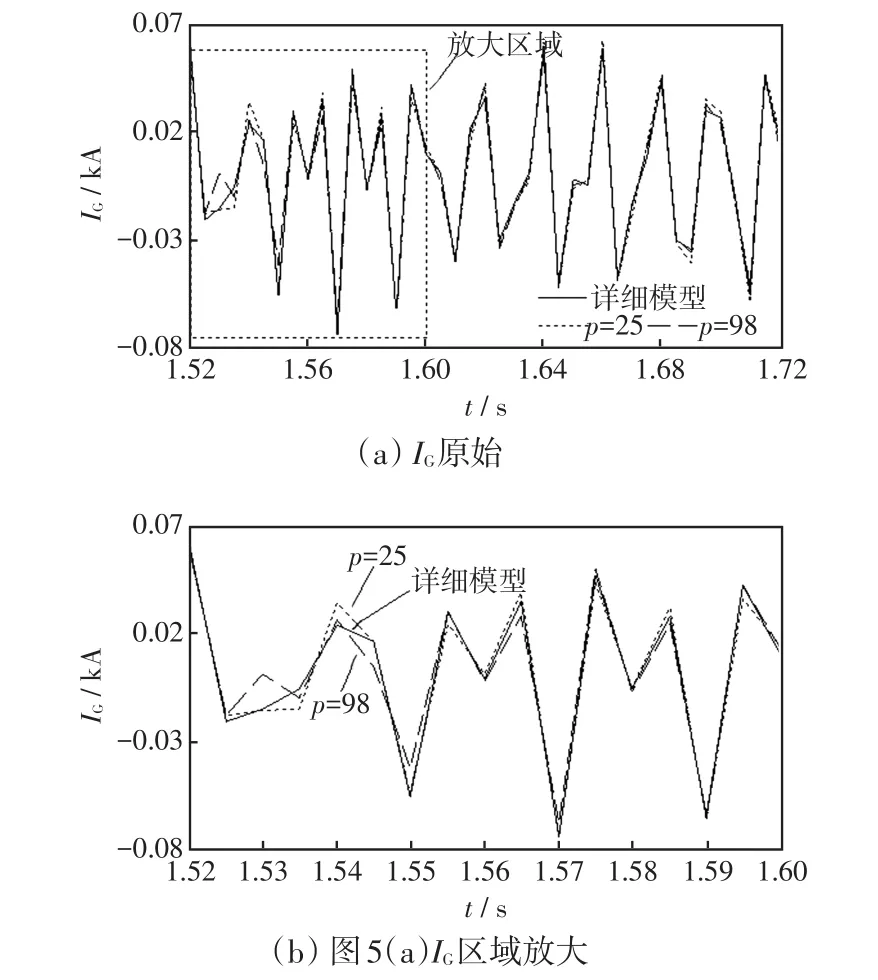
圖5 不同p時IG擬合效果Fig.5 Fitting effects on IGwith different p

表5 不同p等值誤差Tab.5 Error of equivalentce result with different p

由圖4可以看出，即使Prony仿真的階數p很大，占據總能量較多的只占其中一小部分模式，這些模式對參數擬合有較大貢獻，將其視為主要模式。其他模式的能量比ξi幾乎可以忽略不計，對參數擬合的貢獻不大，反而會增加等值模型的復雜度，將其視為雜散模式。

由表3、表4可以發現，盡管階數p不同，但選擇的主要振蕩模式都集中在50 Hz和100 Hz附近，且50 Hz模式能量明顯大于100 Hz。交流電網正常運行時，電網電流的主要分量是基頻交流分量。算例中選取的是故障切除后的電流，此時電網處于正常運行，根據模式能量比選取主要振蕩模式的頻率主要為50 Hz，證明Prony算法分解的結果是有效可信的，根據能量比選取主要振蕩模式是可行的。

由圖5和表5可知，利用能量比可以較為準確地選擇主要振蕩模式，較好地等值風電場出口電流，且在不同的階數p下都有較好的效果；同時，對階數選擇要求不高，降低了Prony算法的使用難度，適用性較好。

3.3 風電場出口特性等值

為驗證由節點模型代替原有風電場詳細模型的可行性，將其與容量加權等值算法的仿真結果進行對比。

方案1：利用容量加權法等值風電場內部參數，將風機群等值為1臺風機。

方案2：通過Prony算法得到風電場出口電流、電壓的振蕩特性參數，利用能量比ξi選取主要振蕩模式，將其線性組合后建立節點模型，代替風電場的詳細模型。

方案3：利用Prony算法得到風電場出口電流、電壓的振蕩特性參數，根據各模式的幅值和衰減因子確定主要模式，將其線性組合后建立節點模型，代替風電場的詳細模型。

方案2、方案3選取的主要模式如表6所示，3種方案的等值誤差如表7所示，方案2、方案3與方案1等值前后對比分別如圖6、圖7所示。

由仿真結果可知，采用Prony算法得到參數振蕩特征參數，利用能量比ξi或幅值、衰減因子篩選的主要振蕩模式都能較好地擬合風電場出口電流、電壓。對比兩者在采樣區間[1.005s，1.245s]內選取的主要模式，后者較前者少選一個模式9；在圖6、圖7中的1.1～1.2 s可以明顯看出，后者較前者誤差增大。利用振蕩模式的幅值和衰減因子的篩選過程簡單、快速，但主觀性較大，可能遺漏主要模式；而利用能量比雖然需要計算每個模式的能量比ξi，比前者運算量大，但其選擇結果較為精確。

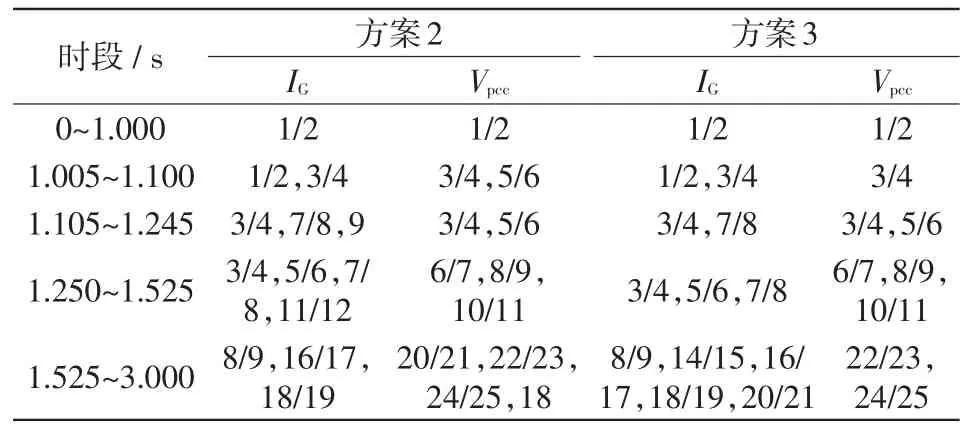
表6 模式選取Tab.6 Selection of mode

圖6 基于能量比的風電場并網點動態響應Fig.6 Dynamic response of wind farm at point of common coupling based on energy ratio

圖7 基于Ai和σi的風電場并網點動態響應Fig.7 Dynamic response of wind farm at point of common coupling based on Aiand σi

表7 3種方案的等值誤差Tab.7 Error of equivalence result with three ways

由Prony方法得到主要振蕩模式，建立節點模型，可等效代替風電場詳細模型。出口電流的等值效果明顯優于容量加權算法，出口電壓雖然存在等值誤差，但總體上能夠反映風電場的動態特性。

4 結論

（1）Prony算法能擬合風電場出口的電流、電壓，但為了保證擬合精度，選擇的階數較高，擬合的電流、電壓模型較復雜，可能引入大量雜散模式。

（2）由于機組間的差異，各臺機組撬棒動作不同步。通過合理劃分采樣區間，保證區間內的振蕩模式盡可能不發生變化，減小撬棒帶來的誤差。

（3）基于幅值和衰減因子的Prony等值算法分析各模式的振蕩特性，以Ai和σi為依據，快速選取對信號影響較大的分量，計算量較小。

（4）基于能量比的Prony等值算法通過分析各振蕩模式的能量比，設置能量閾值，濾除雜散模式，選擇主要振蕩模式，將其線性組合等值風電場出口電壓、電流，有較好的等值效果。同時該算法對Prony算法階數選擇的要求較低。

[1]郝正航，余貽鑫（Hao Zhenghang，Yu Yixin）.雙饋風力發電機組對電力系統穩定性影響（The influence of doublyfed induction generator on stability of power system）[J].電力系統保護與控制（Power System Protection and Con?trol），2011，39（3）：7-11，17．

[2]白鴻斌，王瑞紅（Bai Hongbin，Wang Ruihong）.風電場并網對電網電能質量的影響分析（Influence of the gridconnected wind farm on power quality）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2012，24（1）：120-124．

[3]李生虎，賈豫東，李少飛，等（Li Shenghu，Jia Yudong，Li Shaofei，et al）.定子暫態和運行區域對異步發電機穩定性影響（Influence of stator dynamics and operation zone on stability of induction generators）[J].電工技術學報（Transactions of China Electrotechnical Society），2011，26（S1）：285-291．

[4]盧錦玲，石少通，盧洋（Lu Jinling，Shi Shaotong，Lu Yang）.含大規模風電場的電網靜態電壓穩定性評估（Static voltage stability assessment on the grid with largescale wind farm connection）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2015，27（6）：73-80.

[5]Fernandez L M，Garcia C A，Saenz J R，et al.Equivalent models of wind farms by using aggregated wind turbines and equivalent winds[J].Energy Conversion and Manage?ment，2009，50（3）：691-704．

[6]劉力卿，余洋，王哲，等（Liu Liqing，Yu Yang，Wang Zhe， et al）.變速恒頻雙饋風電機組的動態等值方法（Dy?namic equivalence method of variable speed wind turbine with doubly-fed induction generators）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2012，24（2）：63-66，71．

[7]李輝，王荷生，史旭陽，等（Li Hui，Wang Hesheng，Shi Xuyang，et al）.基于遺傳算法的風電場等值模型的研究（Study on equivalent model of wind farms based on ge?netic algorithm）[J].電力系統保護與控制（Power System Protection and Control），2011，39（11）：1-8，16．

[8]Li Shenghu，Liu Zhengkai，Jia Yudong.Dynamic aggrega?tion of doubly-fed induction generators（DFIGs）for stabil?ity analysis of wind power systems[C]//IEEE Power and Energy Society General Meeting.Detroit，USA，2011．

[9]Thomsen S，Rothenhagen K，Fuchs F W.Online parame?ter identification methods for doubly fed induction genera?tors[C]//IEEE Power Electronics Specialists Conference.Rhodes，Greece，2008：2735-2741.

[10]黃梅，萬航羽（Huang Mei，Wan Hangyu）.在動態仿真中風電場模型的簡化（Simplification of wind farm model for dynamic simulation）[J].電工技術學報（Transactions of China Electrotechnical Society），2009，24（9）：147-152.

[11]張建華，辛付龍，陳星鶯，等（Zhang Jianhua，Xin Fulong，Chen Xingying，et al）.雙饋風力發電機三相短路狀態下的參數辨識（Parameter identification of DFIG with threephase short circuit）[J].電力自動化設備（Electric Power Automation Equipment），2012，32（6）：86-89．

[12]金宇清，趙澤，鞠平，等（Jin Yuqing，Zhao Ze，Ju Ping，et al）.雙饋感應風力發電機的參數辨識分析（Analysis on the identification of double fed induction generator）[J].高電壓技術（High Voltage Engineering），2011，37（7）：1700-1705．

[13]黎芹，張興，楊淑英，等（Li Qin，Zhang Xing，Yang Shuy?ing，et al）.雙饋風力發電機低電壓穿越轉子動態過程分析（Dynamic behaviour of DFIG rotor during low volt?age ride-through）[J].電力系統及其自動化學報（Pro?ceedings of the CSU-EPSA），2010，22（5）：19-24．

[14]朱曉東，石磊，陳寧，等（Zhu Xiaodong，Shi Lei，Chen Ning，et al）.考慮Crowbar阻值和退出時間的雙饋風電機組低電壓穿越（An analysis on low voltage ride through of wind turbine driven doubly fed induction gener?ator with different resistances and quitting time of crow?bar）[J].電力系統自動化（Automation of Electric Power Systems），2010，34（18）：84-89．

[15]Yao Jun，Li Hui，Chen Zhe，et al.Enhance control of a DFIG-based wind-power generation system with seriesgrid-side converter under unbalanced grid voltage condi?tions[J].IEEE Trans on Power Electronics，2013，28（7）：3167-3181．

[16]李生虎.風力電力系統分析[M].北京：科學出版社，2012．

[17]管秀鵬，程林，孫元章，等（Guan Xiupeng，Cheng Lin，Sun Yuanzhang，et al）.基于Prony方法的大型互聯電網PSS參數優化設計（PSS parameter optimization on largescare interconnection power grid based on Prony method）[J].電力系統自動化（Automation of Electric Power Sys?tems），2006，30（12）：7-11．

[18]馬艷峰，趙書強，劉森，等（Ma Yanfeng，Zhao Shuqiang，Liu Sen，et al）.基于改進多信號Prony算法的低頻振蕩在線辨識（Online identification of low-frequency oscilla?tions based on improved multi-signal Prony algorithm）[J].電網技術（Power System Technology），2007，31（15）：44-49，90．

[19]付偉，李興源，洪潮，等（Fu Wei，Li Xingyuan，Hong Chao，et al）.基于Prony辨識的附加最優次同步阻尼控制器設計（Design of optimal supplementary sub-synchro?nous damping controller based on Prony method）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2008，20（5）：10-15．

Dynamical Equivalence to DFIGs Considering LVRT Crowbar Circuit

ZHU Tinghan，LI Shenghu，MA Yanru，BAO Zhengjie
（School of Electrical Engineering and Automation，Hefei University of Technology，Hefei 230009，China）

The motor structure is changing when low voltage ride through（LVRT）occurs.The inconsistent crowbar ac?tion due to the difference between units brings difficulty to the traditional equivalence method，and its equivalence ef?fect is poor.The impact of wind farm on large power grid is mostly related to the dynamic characteristics of its export.In order to improve the equivalence considering LVRT，in this paper，an equivalent model of wind farm is established from the perspective of export characteristics while ignoring its internal structure.The oscillation modes of voltage and current at the wind farm export are analyzed using Prony algorithm.The major oscillation modes are selected to simulate export characteristics by defining the energy ratio，which represents the degree of influence.The effect is compared with that by analyzing amplitude and attenuation of oscillation modes，indicating that this method is more accurate and it re?duces the requirement of model order.The rationality and validity of the equivalent model is verified by simulation con?sidering LVRT.

doubly-fed induction generator（DFIG）；dynamical equivalence；Prony algorithm；low-voltage ride-through（LVRT）；oscillation mode；energy ratio；export characteristics

TM 614

A

1003-8930（2016）11-0025-07

10.3969/j.issn.1003-8930.2016.11.005

2014-08-20；

2016-04-15

國家自然科學基金資助項目（51277049）

朱婷涵（1990—），女，碩士研究生，研究方向為風電系統仿真與動態等值。Email：gracezth@yeah.net

李生虎（1974—），男，博士，教授，博士生導師，研究方向為電力系統規劃與可靠性、風電系統分析與控制、柔性輸電技術。Email：shenghuli@hfut.edu.cn

馬燕如（1990—），女，碩士研究生，研究方向為特高壓直流輸電系統概率仿真。Email：yanruma@mail.hfut.edu.cn