一類非線性高階q-對稱差分方程解的存在性
徐佳寧, 何延生
( 延邊大學 理學院,吉林 延吉 133002 )
摘 要:研究一類非線性高階q-對稱差分方程解的存在性,通過計算得出解的表達形式,利用Banach空間完全連續算子的不動點定理得出解的存在唯一性結果,應用Schaefer's不動點定理得出解的存在性。
?
一類非線性高階q-對稱差分方程解的存在性
徐佳寧, 何延生
( 延邊大學 理學院,吉林 延吉 133002 )
摘 要:研究一類非線性高階q-對稱差分方程解的存在性,通過計算得出解的表達形式,利用Banach空間完全連續算子的不動點定理得出解的存在唯一性結果,應用Schaefer's不動點定理得出解的存在性。
q-對稱差分方程; 解的唯一性; 不動點定理; 解的存在性
0 引言
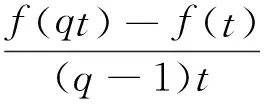
這里q是不等于1的常數,t≠0且f是一個實函數。如果f在t≠0時是可微的,則有

q-對稱微積分在很多領域已被證明實用,尤其在機械學[7-8]中 。近年來,關于q-量子微積分研究有很大進展,關于q-對稱微積分研究較少[9-10]。文獻[9]首先給出關于q-對稱微積分的一些定義;然后建立q-對稱變換問題的一個充分必要條件,即
文獻[10]研究一類二階q-對稱差分方程兩點邊值問題解的存在性,即
首先,利用Banach空間壓縮映像原理獲得解的存在唯一性結果;其次,在一定的邊界條件下,假設非線性項具有超線性和次線性,建立該問題存在正解的充分性條件。筆者研究非線性高階q-對稱差分方程問題,主要研究BVP(1)-(2),即
解的唯一性和存在性。
1 預備知識
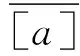
另記
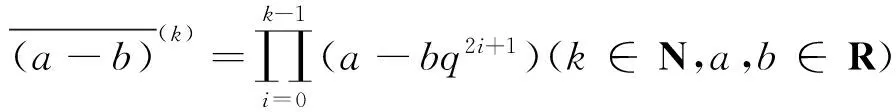
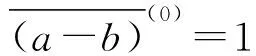
假設q∈(0,1),I是R的一個包含0的區間(有界或無界),表示Iq,即
定義1[10]假定f是一個定義在I上的實值函數,則f的q-對稱差分算子定義為
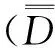
定義2[10]假定a,b∈I,且a 這里 且如果一致收斂于x=a和x=b,則f在[a,b]上是q-對稱可積的。 引理1[10]假設f是一個定義在I上的連續函數,且f在x=0處連續,則對于每一個x∈1,定義 顯然F在x=0處連續。 根據定義1,推出其計算公式。 引理3[10]多重q-對稱積分,即 等價于 這里 證明:利用數學歸納法證明。 當n=2時,有 由引理3得出 假設n=k時成立,當n=k+1時,有 引理4[9]Schaefer's不動點定理:假定C[a,b]是一個Banach空間,算子F:C([a,b],R)→C([a,b],R)是一個完全連續算子,如果集合 E={u=rFu:u∈E,0≤r≤1} 是有界的,則算子F在C([a,b],R)上至少有一個不動點。 建立BVP(1)-(2)問題的解 為得到問題BVP(1)-(2)的解,引入定理。 定理2 假設aq-n 的唯一解為 這里 且滿足條件 (5) 證明:由引理3、式(3)和式(4)知 引理5 對函數Bn(x)有B2k-1(a)=0,k=1,2,…,且當x∈[a,q-(n-2)a)時, 當x∈(q-(n-2)a,b]時 證明: 當x∈[a,q-(n-2)a)時, 當x∈(q-(n-2)a,b]時, 結論成立。 那么邊值問題有唯一的解。 這里 ρn=max{Bn(a),Bn(b),Bn(aq-(n-2))}。 證明:由定理2知問題BVP(1)-(2)有唯一解,可表示為 在C[a,b]定義算子,即 那么對任意的y,z∈C[a,b],有 當n=2k時, 當n=2k+1時, 定理4[9]假設 (1)函數f:[a,b]×R→R是連續的, (2)存在一個N,當N>0時,|f(x,u)|≤N,?x∈[a,b],u∈R, 則BVP(1)-(2)在[a,b]上至少有一個解。 證明:用Schaefer's不動點定理,分4步來證明。 第1步:F是連續的。 令{ym}是一個數列,且ym→y,那么對于任意的x∈[a,b],有 當n=2k時, 當n=2k+1時, 由f的連續性可知 即‖(Fym)(x)-(Fy)(x)‖∞→0。 第2步:F在[a,b]是有界集。 對于任意的η*>0,存在一個常數,即當 時,有‖F(y)‖∞≤。 由定理4得出,對于每一個x∈[a,b],即 第3步:令x1,x2∈[a,b],且x1 綜合步驟1—3可知算子F:C([a,b],R)→C([a,b],R)是完全連續的。 第4步:假設ε={y∈C([a,b],R):y=λF(y),0<λ<1}是有界的,取y∈ε,則y=λF(y),因此,對于每一個x∈[a,b],有 由定理4中條件(2)得對于任意的x∈[a,b],有 因此,對于每一個x∈[a,b],有 可以證明ε是有界的,由Schaefer's不動點定理得出F有一個解 。 研究一類非線性高階q-對稱差分方程解的問題,首先通過計算得出解的表達形式;然后建立Banach空間和完全連續算子F,利用不動點定理得到解的唯一性;最后利用Schaefer's不動點定理證明解的存在性。 [1] Page D N. Information in black hole radiation [J]. Physical Review letters,1993,71(23):3743-3746. [2] Donam Y.q-deformed conformal quantum mechanics [J]. Physical Review D, 2000,62(9):276-284. [3] Jordan C. Calculus of finite differences [M]. New York: Chelsea Publishing Company, 1950:141-145. [4] Ernst T. The different tongues ofq-calculus [J]. Proceedings of Estonian Academy of Sciences, 2008,57(2):81-99. [5] Koekoek R, Lesky P A. Hypergeometric orthogonal polynomials and theirq-Analogues [M]. Springer Berlin Heidelberg: American Mathematical Society, 2010:413-552. [6] Jackon F H.q-difference equations [J]. American Journal of Mathematics, 1910,32(4):305-314. [7] Lavagno A, Gervino G. Quantum mechanics inq-deformed calculus [J]. Journal of Physics Conference Series, 2009,174(1):223-239. [8] Jackson G H. On aq-definite integrals [J]. The Quarterly Journal of Pure and Applied Mathematics, 1910(41):193-203. [9] Brito D C A M C, Martins N. Theq-symmetric variational calculus [J]. Computers and Mathematics with Applications, 2012,64(7):2241-2250. [10] 徐佳寧,侯成敏.一類二階q-對稱差分方程兩點邊值問題解的存在性[J].延邊大學學報:自然科學版,2015,41(3):189-195. Xu Jianing, Hou Chengmin. Existence of solutions for a class ofq-symmetric difference equation two points boundary value problem [J]. Journal of Yanbian University: Natural Science, 2015,41(3):189-195. [11] 張瑜,侯成敏.帶有p-Laplacian算子的分數階多點邊值問題單調正解的存在性[J].東北石油大學學報,2014,38(6):116-125. Zhang Yu, Hou Chengmin. Existence of monotone positive solution for fractional multipoint boundary value problem withp-Laplacian operator [J]. Journal of Northeast Petroleum University, 2014,38(6):116-125. [12] Gasper G, Rahman M. Basic hypergeometric series [M]. Basic Hypergeometric Series: Cambrige University Press, 1990:175-203. [13] Hahn W. Lineare Geometrische Differencezengleichungen [J]. Ferschungszentrum Graz-Statistische Sektion, 1981(66):48-56. [14] Zhang Xinguang, Liu Lishan, Benchawan W, et al. The eigenvalue for a class of singular P-Laplacian fractional differential equations involving the Riemnn-Stieltjes integral boundary condition [J]. Applied Mathematics and Computation, 2014,235(4):412-422. [15] Benchohra M, Hamani S, Ntouyas S K. Boundary value problems for differential equitions with fractional order and nonlocal conditions [J]. Surveys in Mathematics and Its Applications, 2008,71(7-8):2391-2396. 2016-06-23;編輯:關開澄 國家自然科學基金項目(11161049) 徐佳寧(1992-),女,碩士研究生, 主要從事偏微分方程方面的研究。 何延生,E-mail:a13039337970@126.com O175.6 A 2095-4107(2016)05-0114-09 DOI 10.3969/j.issn.2095-4107.2016.05.014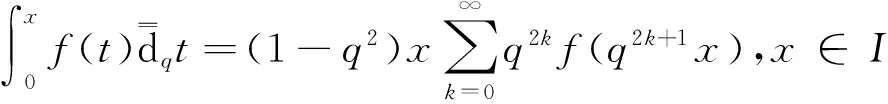
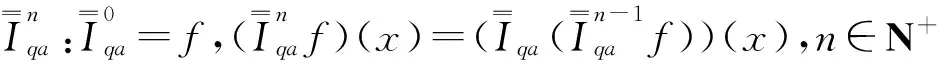
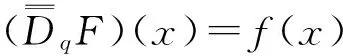
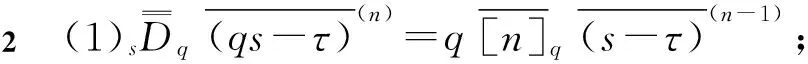
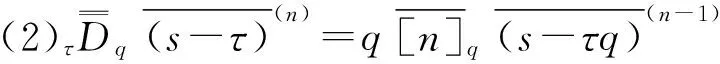
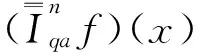
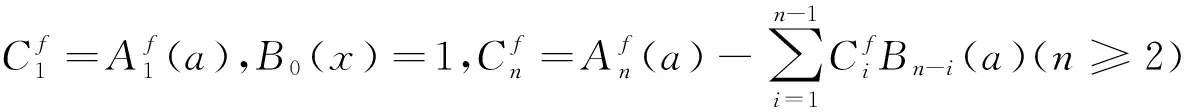
2 解的表達形式

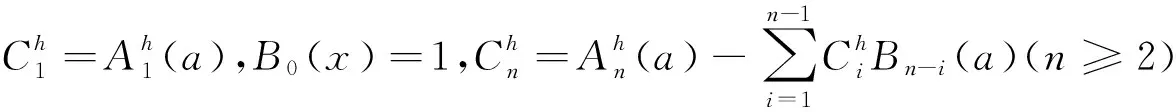
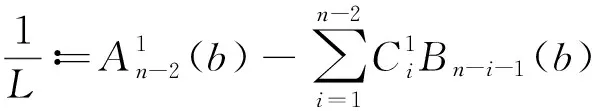
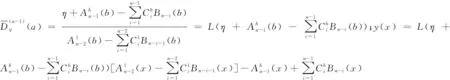
3 解的唯一性
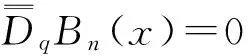
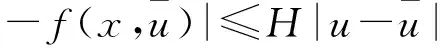
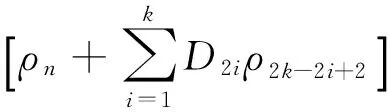
4 解的存在性

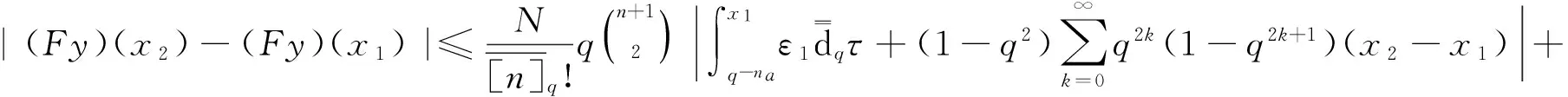
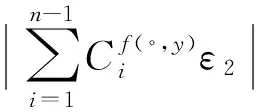
5 結束語

