基于MEMS的運動體姿態角度測量系統設計與實現

徐萬芝 高國偉 潘宏生 楊寰 毛瑞燕

1.北京信息科技大學傳感器重點實驗室，北京100192；

2.北京國科艦航傳感技術有限公司，北京 100101

3.北京機械設備研究所物資供應室，北京 100039

一、引言

隨著我國工業技術的不斷發展，姿態測量廣泛應用于各個領域中，無論是定位、定向，還是導航都離不開姿態測量。運動體姿態測量系統是提供運動體三軸的角速率、俯仰角和橫滾角信息的裝置，是運動體實現姿態控制的前提，它不僅可以為運動體姿態控制系統提供三維姿態信息，也可以為數據記錄器提供運動體的三維姿態信息以備事后分析。

隨著微電子技術的發展而出現的微電子機械系統（MEMS）具有尺寸小、重量輕、成本低、功耗小和動態范圍寬等優點，被廣泛應用于測量領域[1,2]。本文應用MEMS技術，設計出一種成本低、性能好、功耗低的運動體姿態測量系統，能較好的實現運動體姿態角度的測量。

二、系統總體設計

系統基本的結構框圖如圖1所示。 本文選用六軸運動處理組件，包含了三個單軸的加速度計和三個單軸的陀螺儀，加速度計測量運動體在坐標系統中獨立三軸的加速度信號，而陀螺儀檢測運動體相對于導航坐標系的角速度信號，從而測量運動體在三維空間中的角速度和加速度。本文的設計思路是通過慣性測量模塊測量運動體的加速度和角速度信號，再經微處理器模塊進行姿態解算，進而得出運動體的姿態信息，最后通過串口通信模塊將數據傳輸到上位機，得到實時且可視化的姿態信息。

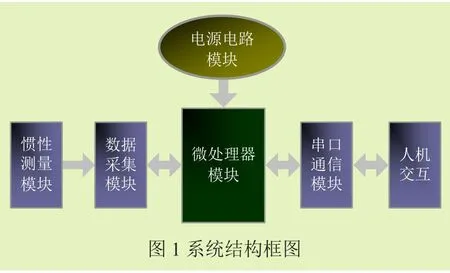
三、系統硬件設計

1、微處理器模塊

本系統微處理器模塊選用STM32F103C8T6，這是意法半導體公司 生 產 的ARM 32位 的Cortex?-M3 CPU，工作頻率最高可達72MHz，內置高速存儲器，擁有64K字節的閃存和20K字節的SRAM，豐富的增強I/O端口和聯接到兩條APB總線的外設，工作電壓范圍在2.0～3.6V，具有高速性、低成本、高性價比等優點。STM32F103C8T6的最小系統如圖2所示。

2、慣性測量模塊

慣性測量模塊是姿態測量系統的重要組成部分，本系統所選用的是硬件為MPU-6050模塊。MPU-6050是一個可直接使用的模塊，整合了MPU-6050芯片、供電電路及其端口電路，測量精準且性價比較高。MPU-6050芯片設有3個16位模擬-數字轉換器，用于數字化陀螺儀和加速度計輸出。用戶可對陀螺儀和加速度計進行編程控制，陀螺儀滿量程測量范圍為 ±250、±500、±1000與 ±2000°/s，加速度計滿量程測量范圍為±2g、±4g、±8g與±16g，對于快速和慢速運動可進行精確跟蹤。模塊實物及端口電路如圖3所示。

MPU-6050芯片是全球首例整合性六軸運動處理傳感器，它消除了組合陀螺儀與加速度計時存在軸間差的問題，使封裝空間得到了大量減少，消除了加速度計與陀螺儀的軸間敏感度，降低了人為設定產生的影響與傳感器的漂移。內含數字運動處理(DMP: Digital Motion Processing)引擎，可減少復雜的融合演算數據、傳感器同步化、姿勢感應等的負荷。MPU-6050芯片連接電路如圖4所示。

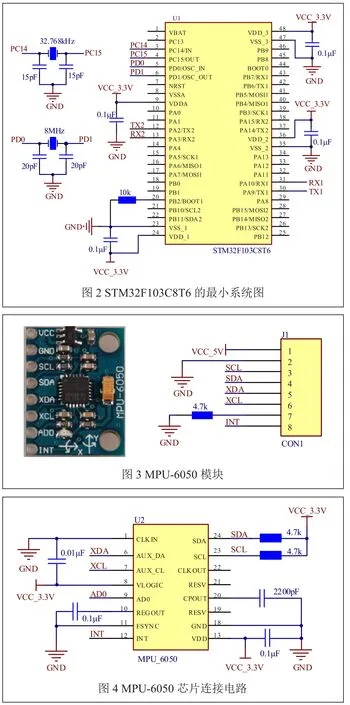
MPU-6050的供電電壓為3.3V，通過一個低壓差線性穩壓器供電，電路圖如圖5所示。

3、串口通信模塊

為了將計算得到的運動體姿態信息顯示出來，我們采用RS232 接口與PC機進行交互通信。一方面，PC機實時接收運動體的加速度和角速度等參數；另一方面，可通過PC機對測量系統的工作參數進行補償設置。STM32103C8T6的最高工作電壓3.6V，但與RS232的電壓標準本不匹配，故而本系統采用MAX3232 芯片來實現電平轉換。串行通信接口電路如圖6所示。

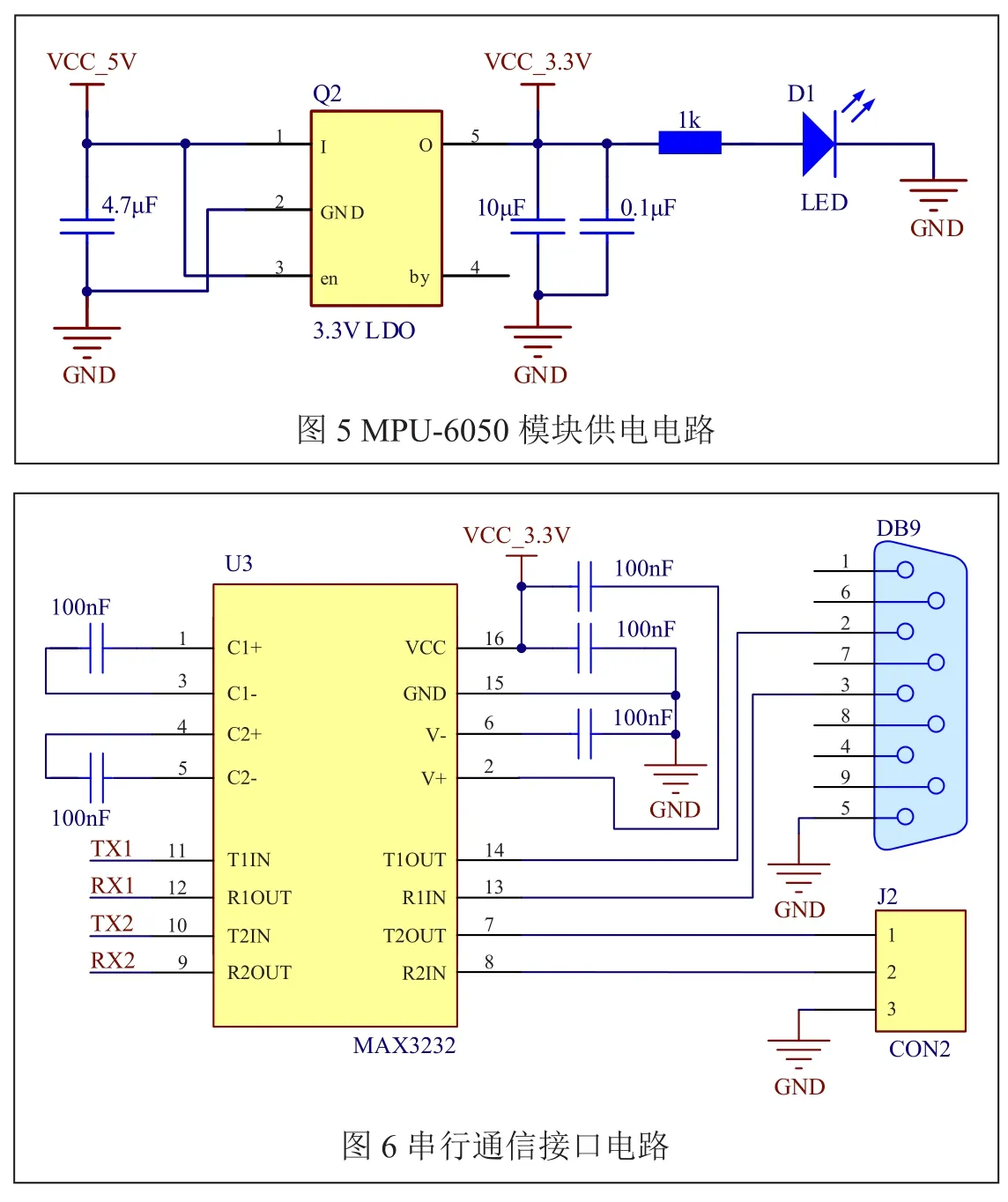
四、系統軟件設計

1、姿態解算原理

運動體的姿態解算算法是實現運動體姿態精確測量的核心技術之一。目前描述動態坐標系方位關系的方法有多種，主要分為三個類別：歐拉角法、方向余弦法、四元數法。其中，歐拉角法存在“奇點”現象，不能用于全姿態運動載體上，且實時計算較為困難。方向余弦法雖然避免了歐拉角法的“奇點”現象，但方程的計算量較大，使得工作效率降低[3]。相比于前兩類方法，四元數法能更加合理有效地描述載體的剛體空間運動，因此本系統選用四元數法進行姿態解算。

四元數微分方程的表達式為：

其中，Ωb—運動體坐標系相對地理坐標系的旋轉角速度的斜對稱矩陣。

式（1）可擴展為：

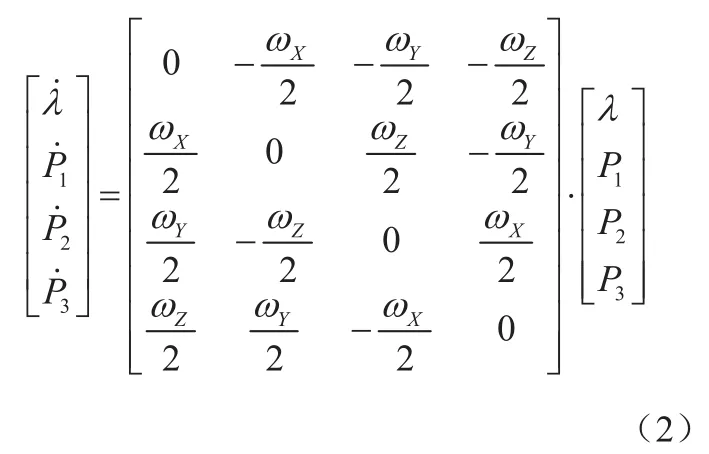
其中，λ、P1、P2、P3—四元數的四個元；

ω—運動載體坐標系相對參考坐標系的旋轉角速度，且有：

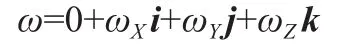
采用和矩陣微分方程式求解相似的方法，求得：

其中，I—單位四元數。

（3）式為四元數微分方程式的解， 且有：

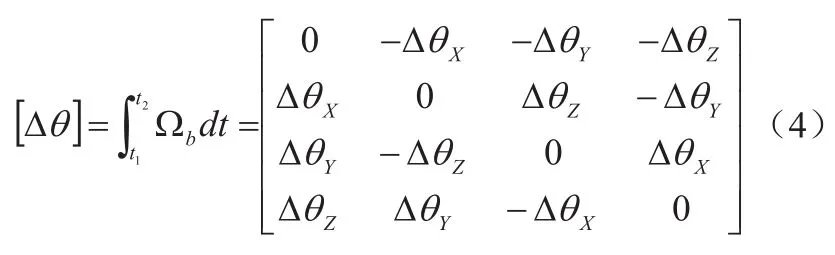
通過矩陣實時計算，由四元數可確定出運動體機體軸確定的坐標系M到導航坐標系E的坐標變換矩陣：

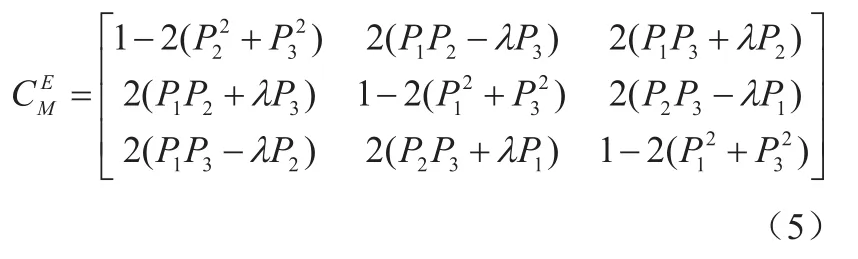
設運動體的航向角為Ψ，俯仰角為θ，橫滾角為γ，選取導航坐標系為地理坐標系，地理坐標系可由三次基本旋轉得到運動體的機體坐標系，其坐標變換矩陣為：

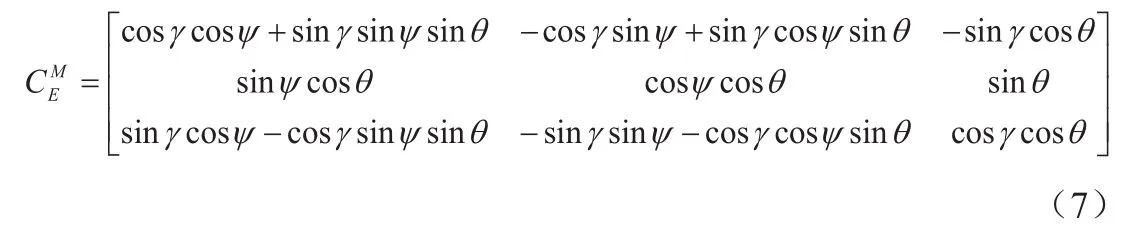
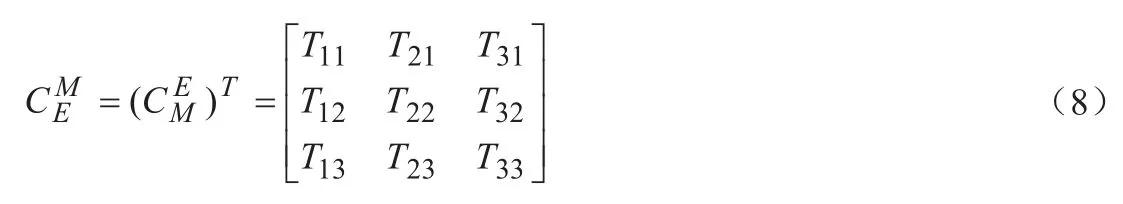
通過式（7）和式（8）可得：

通過上述分析可知：若表征坐標系變換的旋轉四元數以確定，則按式（6）可計算出姿態矩陣，再按式（9）即可確定出運動體的航向角、俯仰角和橫滾角[4～7]。

2、系統主程序設計

系統軟件設計的主程序流程圖如圖7所示。首先進行的是系統初始化，主要任務有確定運動體的初始信息，如初始位置、初始速度等；數學平臺的初始對準，以確定姿態矩陣的初始值；慣性器件的初始校準，對MPU-6050的各標度因數進行標定。然后進行姿態矩陣的更新計算，以提供運動體姿態以及計算姿態參數時的必要數據，這是算法中最重要的一部分。最后進行姿態計算，以獲取個姿態參數，并對獲得的參數進行提取驗證。

五、測試結果及分析

本系統的測試過程是通過SGT320E型三軸轉臺來完成的，如圖8所示，它是U—O—O結構，即臺體由U形外框、O形中框以及O形內框組成，三軸均可連續無限旋轉，既可單軸旋轉也可多軸旋轉，它可以精確地提供系統在工作期間可能經受的各種形式的角運動模式。當轉臺采用本機控制方式時，三軸均具有速率模式、位置模式和正弦擺動模式，通過串口仿真控制轉臺以設定的方式轉動，可為待測系統提供更為復雜的仿真測試環境。

本系統的測試方法為設定三軸轉臺的旋轉速率為10°/s和20°/s 對系統分別進行兩次測量，得到兩組測量數據，測量過程中各方向角單獨測量，其他方向角置零位。俯仰角和橫滾角的測量范圍都是-90°～+90°，每10°一測，航向角的測量范圍是0°～360°，每20°一測。經過測量得到俯仰角，橫滾角，航向角的測量數據，各角度誤差如圖9、圖10、圖11所示，其中測量數據中第一組轉臺旋轉速率為10°/s，第二組轉臺旋轉速率為 20°/s 。

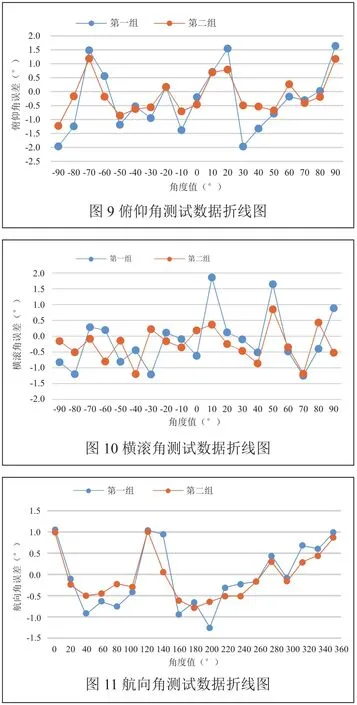
通過測量數據可知，系統俯仰角測量的角度誤差基本保持在±2°以內，橫滾角測量的角度誤差除個別點以外基本保持在±1.5°以內，航向角測量的角度誤差則較好地保持在±1.5°以內，且在轉臺不同的轉動速率下，轉動速率對系統的測量有一定影響，但測量誤差基本都保持在一定的誤差范圍內。可見，系統對運動體姿態角度的檢測具有較好的測量效果，系統設計可行。

六、結束語

本文應用慣性傳感器模塊MPU-6050，設計了一款高性價比、高穩定性、低功耗的運動體姿態角度測量系統，可實時測量顯示運動體各姿態角的角度。實驗結果顯示，該系統測量角度較為準確，在各姿態角的測量過程中，最大測量誤差不超過2°，且系統測量穩定性較高，達到了系統設計的測量目的。