隨機訪問網絡后退避機制的性能分析

步超倫，肖揚，葉通，吳鵬，張小建，吳軍民

（1.上海交通大學區域光纖通信網與新型光通信系統國家重點實驗室，上海200240；2.國網智能電網研究院，江蘇南京210003）

研究與開發

隨機訪問網絡后退避機制的性能分析

步超倫1，肖揚1，葉通1，吳鵬2，張小建2，吳軍民2

（1.上海交通大學區域光纖通信網與新型光通信系統國家重點實驗室，上海200240；2.國網智能電網研究院，江蘇南京210003）

無線局域網隨機訪問協議的性能分析是近年來的研究熱點，而現有的模型還未能對其后退避機制進行有效刻畫。基于一種兩階段的馬爾可夫模型，分析非飽和業務狀態下隨機訪問網絡的性能。首先，利用嵌入式馬爾可夫鏈描述每個站點隊頭分組的服務過程，引入虛擬服務時間的概念，即將傳輸成功之后的后退避也看成隊頭分組服務時間的一部分，從而得到隊頭分組的虛擬服務時間分布。然后，將每個用戶隊列看成一個Geo/G/1系統，求得非飽和業務狀態下系統吞吐量、時延等參數的閉合解表達式以及系統的穩定區間。仿真結果驗證了模型的準確性。本文所提模型將對今后研究無線局域網的分布式協調功能（DCF）協議打下基礎。

隨機訪問網絡；后退避；性能分析；馬爾可夫鏈

1 引言

近年來，人們對移動通信以及帶寬的要求越來越高，無線局域網絡的應用越來越廣泛。無線信道的隨機訪問協議是無線局域網的核心協議，其中較常見的隨機訪問協議有Aloha協議及其變種載波偵聽多路訪問（CSMA）協議和分布式協調功能（DCF）協議等。

隨機訪問網絡協議的一個突出問題是信道的捕獲效應，即信道被同一站點持續占用，而其他站點則一直處在退避重傳的過程中無法成功發送數據，從而帶來節點間的不公平性。為了解決這一問題，業界引入了“后退避”機制，即在數據分組發送成功之后，站點進行一段隨機退避，以便釋放信道，從而避免信道被某個站點持續占用。

過去的十幾年里，許多學者對基于后退避機制的隨機訪問協議進行了分析，然而大多數分析都是基于飽和業務假設。所謂飽和業務情形，就是指各站點在發送成功數據分組后，緩存隊列中一定有數據在等待發送。在該情形下，當數據分組到達隊列時，站點要么在忙于發送數據分組，要么在進行“后退避”。Bianchi［1］提出了一種二維的馬爾可夫鏈模型來刻畫數據分組過程，并對系統的吞吐量進行了分析。參考文獻［2-5］針對飽和業務情形下的隨機訪問協議系統進行了分析，然而他們都基于參考文獻［1］中飽和業務情形的假設。在實際系統中，網絡一般不會工作在飽和業務情形下，因為此時的網絡均處于非穩定狀態，數據時延性能得不到保障。研究非飽和業務情形下系統的性能具有十分重要的意義。

在非飽和業務情形下，數據分組到達隊列時看到的情形要比飽和業務復雜得多。當有新的數據分組到達站點時，該站點可能正在忙于發送隊頭分組，也可能正處于后退避狀態，還可能處于空閑狀態。目前，已經有一些文獻對非飽和業務情形下的隨機訪問網絡進行了分析。參考文獻［6］是基于參考文獻［7］的兩階段模型，分析了非飽和業務狀態下的DCF系統性能，但未考慮后退避機制。參考文獻［8，9］在參考文獻［1］的馬爾可夫鏈的基礎上，增加了站點空閑的狀態，并分析了非飽和業務狀態下系統的特性，但仍然沒有考慮后退避機制。Malone［10］則針對非飽和業務的特性，在馬爾可夫鏈［1］的基礎上增加了后退避狀態，然而在分析系統的吞吐量和時延時，涉及站點的空閑概率，而該概率本身又取決于系統的狀態，這就產生了記憶性，沒法求出各參數的封閉解析表達式。

為此，本文提出虛擬服務時間的概念，并基于一種兩階段模型［7］分析非飽和業務情況下的后退避的隨機訪問網絡性能。假設當共享媒介的站點數量較多時，站點間的行為相互獨立，即每個站點看成獨立的FIFO隊列。首先，利用馬爾可夫鏈描述每個站點隊頭分組的服務過程，引入虛擬服務時間的概念，即將傳輸成功之后的后退避過程也看成隊頭分組服務時間的一部分。于是，上述隊頭分組可能面對的復雜情形變得清晰，一個分組到達站點時，要么站點處于繁忙狀態，要么處于空閑狀態，這樣就消除了系統的記憶性，體現出模型的馬爾可夫特性。然后，將每個用戶隊列看成一個Geo/G/1系統，求得非飽和業務狀態下系統吞吐量、時延等參數的閉合解表達式，并確定系統的穩定區間。

2 物理過程及模型建立

本文研究的隨機訪問網絡如圖1所示，多個站點通過隨機競爭的方式共享同一個帶寬資源。該網絡是一個分時隙的系統，每個站點都服從速率為λ的伯努利到達過程，并且都帶有無限空間的緩存。

圖1 n個站點的時隙隨機退避網絡模擬隊列

圖2演示了基于后退避的時隙隨機訪問網絡中兩個站點競爭發送分組的過程。當一個數據分組成為隊頭分組，而且該站點不處于后退避狀態時，站點將在當前時隙立即發送它。如果此時另一個站點在此時隙也有分組發送，就會發送沖突，如圖2中灰色方框所示。這時兩站點都要進行一段隨機時間的退避，即以概率q重傳該數據分組，如圖2中實線箭頭所示；當某個時隙只有一個站點發送數據分組時，數據分組可以傳送成功。但為了避免成功站點獨占信道，該站點將以概率r進行一段后退避，如圖2中虛線箭頭所示。

圖2 基于后退避的時隙隨機訪問網絡中兩個站點競爭發送分組的過程

在后退避的隨機訪問網絡中，站點的數據分組看到的本站所處的狀態會比較復雜。當此分組到達站點時隊列非空，它成為隊頭分組后仍需要經歷一個后退避的過程才能被發送；如果此分組到達時隊列為空，但站點后退避過程并未結束，它也需要等到后退避過程結束后才能被發送；如果此分組到達時隊列為空，且上一次后退避已經結束，則可以在當前時隙立即被發送。因此，新到達的分組是否能被立即發送，不僅取決于站點隊列是否為空，而且取決于站點是否處于后退避狀態，這使非飽和業務下的性能分析變得困難。參考文獻［1］中假設飽和業務，實際上是只考慮第一種情形，減小了問題復雜度，因此不符合一般情形。

為了全面刻畫后退避狀態，本文引入虛擬服務時間的概念，即將后退避過程看成一個隊頭分組服務過程的一部分。換言之，從一個分組成為隊頭分組到由它引發的后退避結束的這段時間看成虛擬服務時間。在這段時間內，站點都屬于“忙”的狀態。只有后退避結束之后，隊列的下一個分組才能成為一個隊頭分組。如圖3所示，用Ps表示第s個數據分組，用Xs表示數據分組s的真實服務時間，Bs表示數據分組Ps的后退避的時間，隊頭分組服務過程的虛擬服務時間則由單個分組的真實服務時間Xs和后退避時間Bs兩部分構成，即Vs=Xs+Bs。于是，上述隊頭分組可能面對的復雜情形變得清晰。一個分組到達站點時，站點要么處于繁忙狀態，要么處于空閑狀態，而且引入虛擬服務時間的概念也不影響真實的平均服務時間的計算。因為，只要把平均虛擬服務時間減去平均后退避時間就可以得到真實的平均服務時間。

圖3 虛擬服務時間

本文基于參考文獻［7］的兩級排隊模型對系統進行建模。把每個站點看成一個Geo/G/1的排隊系統，其中信道對隊頭分組的服務過程可以通過圖4的馬爾可夫鏈來刻畫。隊頭分組將經歷可直接發送狀態（狀態0）、發送失敗后的重傳狀態（狀態1）以及發送成功后的后退避狀態（狀態-1）。新的隊頭分組都是先進入初始狀態0，如果傳送發生沖突則進入狀態1，并以概率q再次發送；而如果隊頭分組以概率p傳送成功，則以概率r回到狀態0，以概率1-r進入狀態-1。同樣，如果處于狀態1的隊頭分組再次沖突，則依然處于狀態1，如果傳送成功則以概率r選擇是進入狀態-1還是狀態0。因此，參數r描述了站點在成功發送分組之后的時隙中，進行后退避過程的概率。換言之，參數r也決定了一個站點處于后退避狀態的時長。

圖4 帶有后退避機制的時隙隨機退避網絡隊頭分組服務過程馬爾可夫鏈

用f0、f1和f-1分別代表圖4中各狀態的穩態概率。利用離散時間馬爾可夫鏈的性質，可以得到：

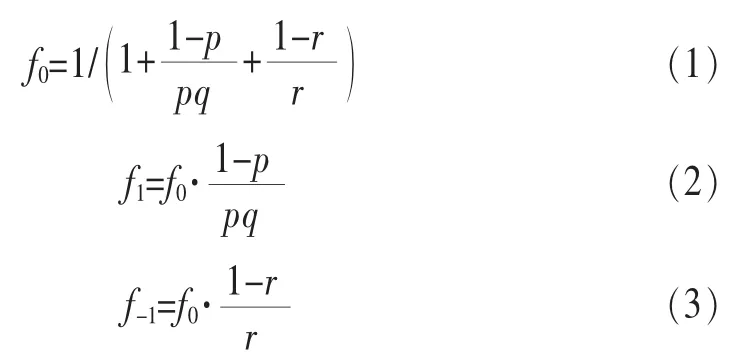
因為后退避過程也可看成隊頭分組服務過程的一部分，把引入后退避機制后數據分組的到達速率和虛擬服務速率的比值稱為虛擬負載率ρυ。每一個隊頭分組的起始狀態是0，而結束狀態也是0，因此一個隊頭分組的服務速率是f0，假設輸入速率為λ，每個站點的虛擬負載率為：

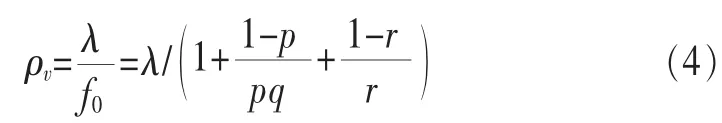
3 性能分析

3.1 吞吐量

每個站點可能存在5種狀態：狀態1，空閑且緩存為空；狀態2，忙于傳送一個狀態為0的新分組；狀態3，忙于重傳一個狀態為1的發生過沖突的分組；狀態4，由于傳送發生沖突而進行退避；狀態5，進行后退避。

由式（1）～式（4）可知，Pr｛狀態1}=1-ρυ，Pr｛狀態2}=ρυf0，Pr｛狀態3}=ρυf1q，Pr｛狀態4}=ρυf1（1-q），Pr｛狀態5}=ρυf-1。

當站點處于狀態1、4和5時，并不會發送數據分組。而一個站點想要成功發送分組的條件就是其余n-1個站點不發送分組，那么成功發送分組的概率為：

在穩定狀態下，系統的輸出λout應該和輸入λin相等，根據式（5）可知，每個時隙的平均嘗試發送分組率為：

所以穩定狀態下的吞吐量為：

這與參考文獻［11］中的結果是一致的，這說明本文模型在吞吐量上的分析是正確的。

3.2 時延

由圖4可知，隊頭分組的服務時間是在所有狀態經歷時間的總和，用Di表示從狀態i開始直到服務完成所經過的時間，用Yi表示在狀態i所花費的時間，有：

Yi是服從幾何分布的隨機變量，Yi的概率母函數為：

根據式（8）和式（9），Di的概率母函數可以表示為：

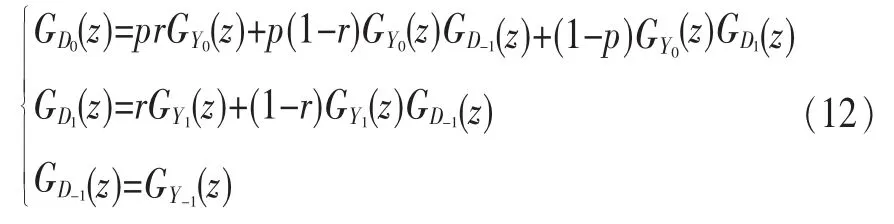
根據式（11）和式（12），有：

根據概率母函數的性質可知，虛擬服務時間V的均值和方差可以表示為：

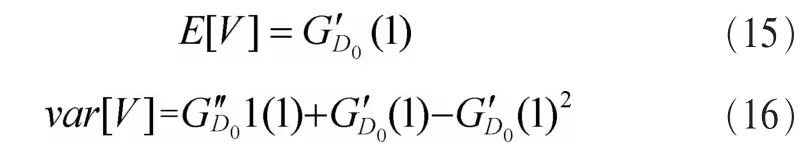
根據參考文獻［7］中的Pollaczek-Kintchine公式以及式（13）～式（16），可以得到平均虛擬服務時間為：

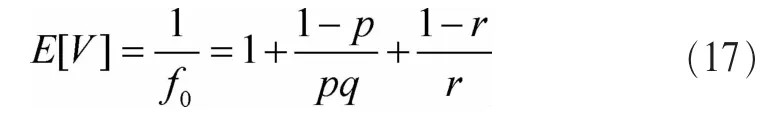
平均等待時間為：

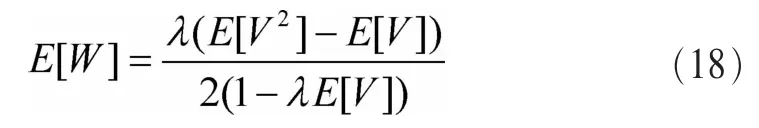
計算平均總時延時，應將平均虛擬服務時間和平均等待時間相加后，再減去平均后退避時間，即：

3.3 穩定區間

根據參考文獻［11］，時隙隨機退避網絡的最大吞吐量約為0.368，由式（7）可以得到系統吞吐量與嘗試發送率之間的關系，如圖5所示。

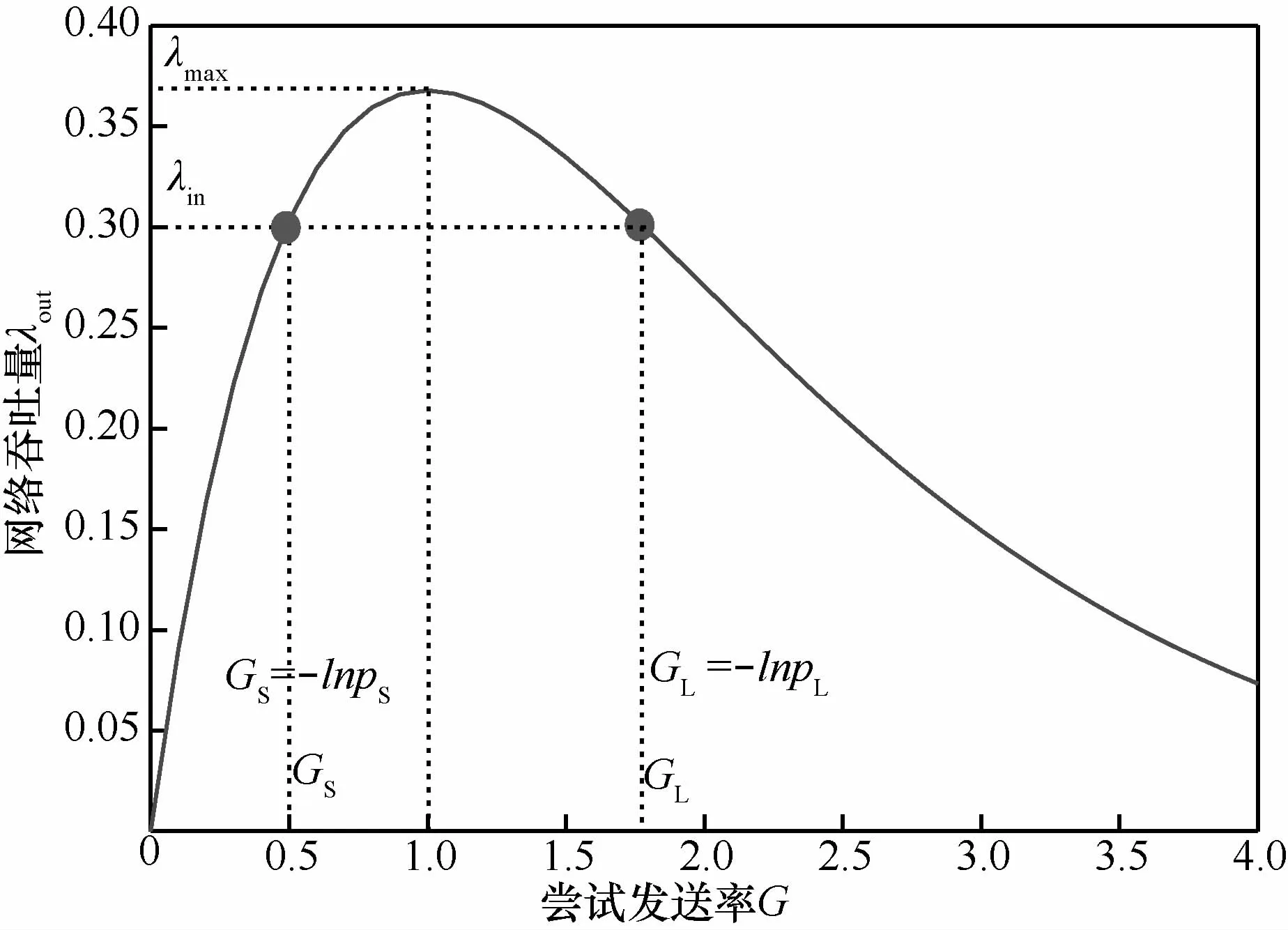
圖5 λout與G的關系曲線

假定系統總輸入λin=nλ＜0.368，那么系統穩定的條件就是λout=λin=nλ。對應圖5中可以發現，只有在兩個紅色實心交點處滿足該條件，把這兩個交點分別記作GS和GL，根據式（6）可以得到對應的兩個成功發送分組概率分別為pS和pL。

q是唯一一個可以由系統改變的參數，系統只有當ρυ≤1時才會處于穩定狀態，所以令ρυ=1，求出臨界狀態下的兩個q值。由式（4），有：

代入pL和pS有：

系統穩定時需要滿足兩個條件，即ρυ≤1且E［T］＜∞，下面將分5種情形分別討論關于q的穩定區間。

（1）情形1：q∈［0，qS）

將q代入式（4）和式（19）可知，無論p取何值，都會得到ρυ＞1且E［T］=∞，在這種情況下系統一定不穩定。

（2）情形2：q=qS

這種情形下，p=pS可以得到ρυ=1，系統處于臨界穩定，然而此時E［T］=∞，系統并不穩定。

（3）情形3：q∈（qS，qL）

這種情形下需要對p的取值分情況進行討論，當p=pS時，ρυ＜1，且ρυ隨著q的增加而降低，E［T］有上界，且E［T］隨著q的增加而逐漸降低，此時系統穩定；而當p取pL時，ρυ≥1，系統不穩定，E［T］為負值，顯然不可能。這說明，在這個區間內系統要想穩定，其發送分組成功概率p一定只能等于pS。

（4）情形4：q=qL

當q=qL時，p=pL，ρυ突然增加到1，系統處于臨界狀態，而E［T］突然又增加到無窮，系統不穩定。

（5）情形5：q∈（qL，1］

此時無論p取pL還是pS，ρυ＜1均成立，且E［T］均有界。這似乎暗示著系統可以同時處于pL和pS狀態，然而模型各態遍歷的前提說明模型在此區域已經失效，系統在穩定狀態下p不可能有兩個解，即模型無法刻畫系統的行為。

綜上，系統的穩定區間為q∈（qS，qL）。并且當q∈［qS，qL）時，站點發送分組成功概率為p=pS；當q=qL時，站點發送分組成功概率為p=pL。因此，在qS≤q≤qL區間內，p是q的階躍函數。

4 仿真與分析

在C++的環境下對每個站點隊頭分組的不同狀態進行仿真，默認取站點個數n為50，并且令r=q，分別在3種不同的系統輸入流量λin=0.1、0.3和0.35的情況下進行對比仿真，只設置一個可調參數：重傳因子q，接下來通過設置不同的q值，得到吞吐量、時延、負載率等參數的仿真結果。

圖6是吞吐量λout在不同的系統輸入流量下關于重傳因子q的仿真結果比較。可以看出，穩定區間的仿真結果邊界值與用式（21）和式（22）計算的理論值（qSqL）相符，當重傳因子q超出穩定區間時，系統的吞吐量快速下降，而當重傳因子q在穩定區間（qS，qL）內時，系統吞吐量λout始終保持恒定，即系統輸入流量λin。

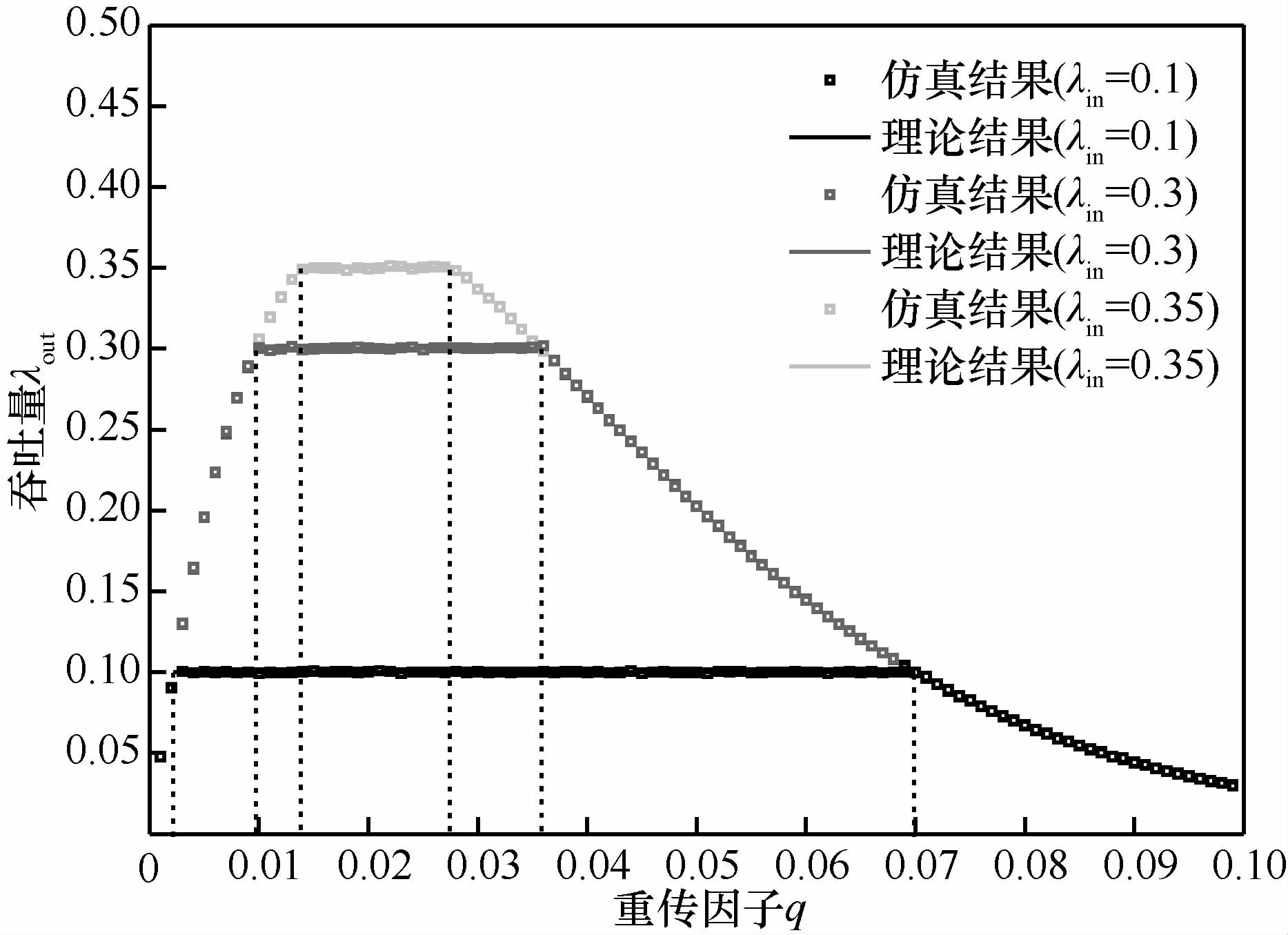
圖6 吞吐量的仿真結果比較

圖7則對系統的平均總時延進行仿真。可以看出，仿真結果可以和式（19）算出的理論結果相匹配。當重傳因子q在穩定區間內逐漸增加時，平均時延從無窮大開始逐漸下降，這是因為隨著q的增加，各站點在發生沖突后的重傳概率變大，那么出現某個站點持續占用信道的概率減小，也就是增加了系統的公平性，站點的緩存中排隊等待發送的數據分組變少，站點中隊頭分組發送沖突后退避的時間也減少，從而降低了平均時延。而當重傳因子q超出穩定區間后，時延突然增加到無窮大，系統狀態又變為不穩定。

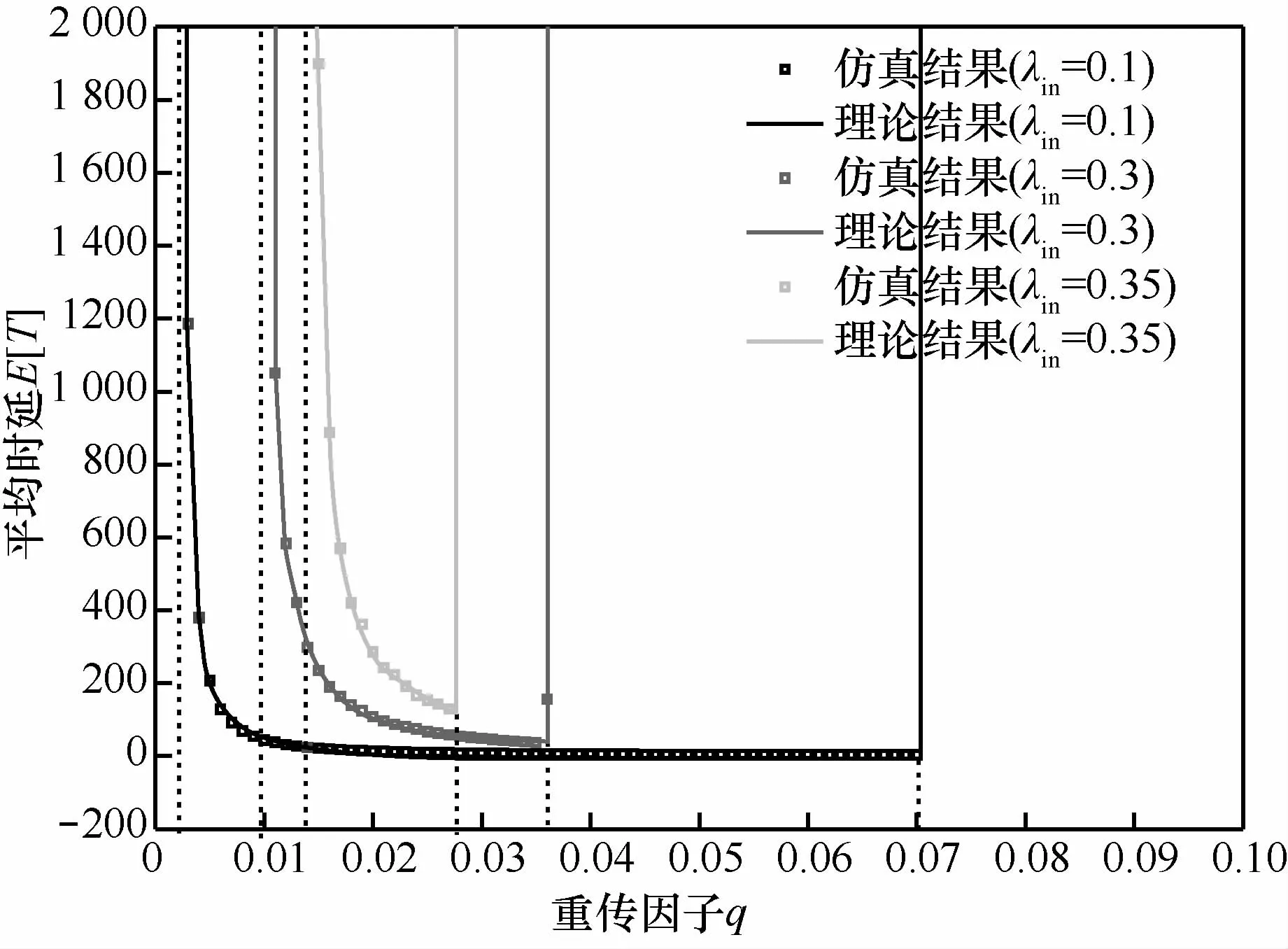
圖7 平均時延的仿真結果比較

圖8則是虛擬負載率ρυ關于q的關系曲線。在穩定區間內，仿真結果與式（4）的理論值相符。虛擬負載率ρυ等于數據分組的到達速率和虛擬服務速率的比值，隨著q的增加，站點中隊頭分組發送沖突后退避的時間減少，也就是服務時間減少，即服務速率增加，那么在到達速率λ不變的情況下，虛擬負載率ρυ是關于q的一條單調遞減曲線。而在穩定區間的兩個端點處，負載率為1，系統處于臨界穩定。

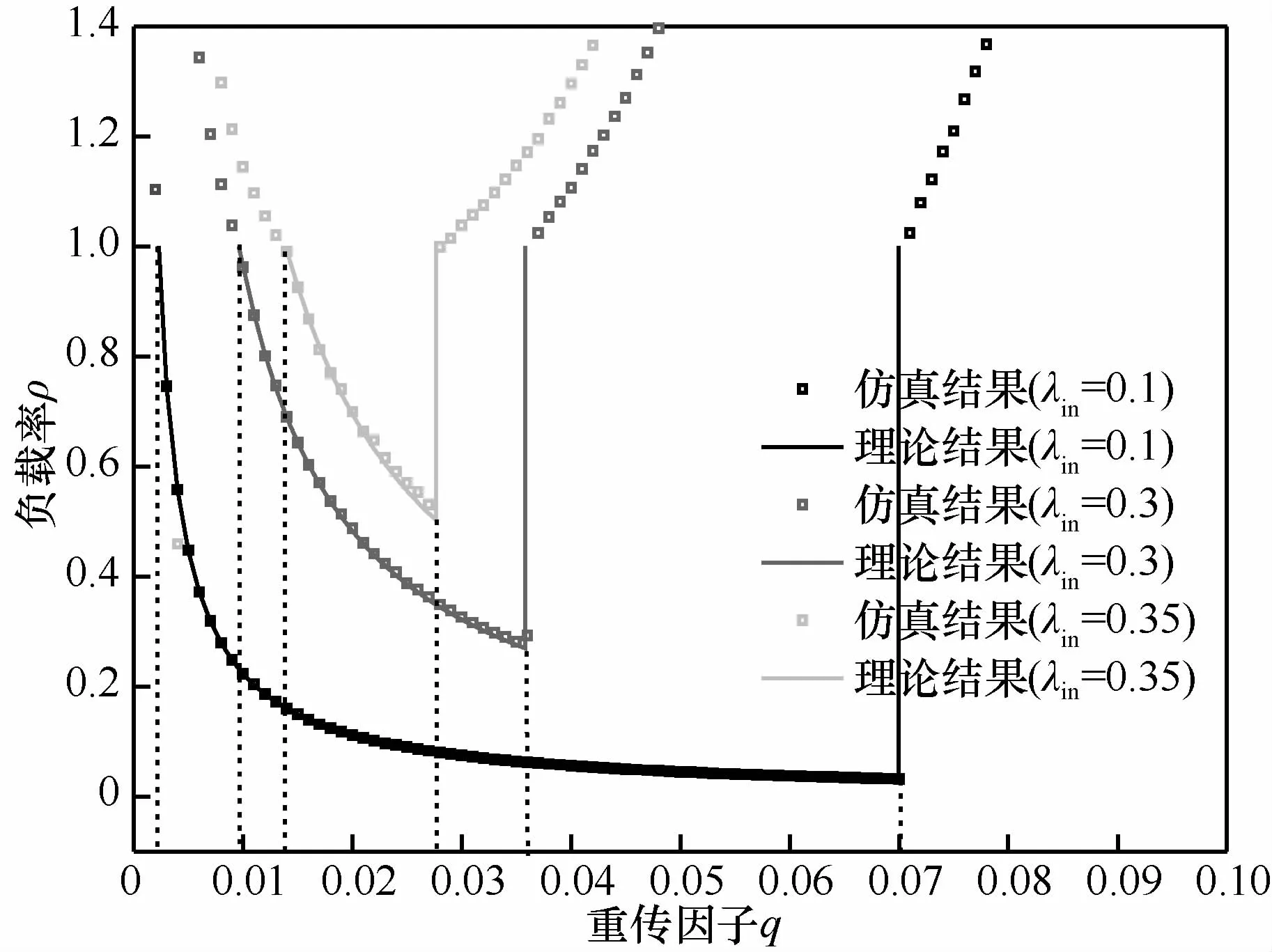
圖8 系統負載率的仿真結果比較

當q∈［qS，qL）時，站點成功發送分組的概率p始終等于pS；而當重傳因子q=qL時，站點發送分組成功概率為p=pL。成功發送分組概率的仿真結果如圖9所示。在［qS，qL）內，p始終保持恒定且等于pS，而當q=qL時，p發生跳變，變為pL，這又進一步驗證了理論分析中所預測的階躍性是正確的。

圖9 成功發送分組概率的仿真結果比較

5 結束語

本文提出了一種帶有后退避機制的馬爾可夫鏈模型，以分析時隙隨機退避網絡協議的性能。通過引入的虛擬服務時間和虛擬負載率等參數，分析了系統各項參數的性能，并求解出非飽和業務狀態下系統吞吐量、時延等參數的閉合解表達式以及系統的穩定區間。仿真結果與理論分析相符，證實了本文模型的正確性。接下來將分析后退避機制在更加復雜的隨機退避網絡協議（如分布式協調功能（DCF）協議）中的應用。

［1］BIANCHI G.Performance analysis of the IEEE 802.11 distributed coordination function［J］.IEEE Journal on Selected Areas in Communications，2000，18（3）：535-547.

［2］KUMAR A，ALTMAN E，MIORANDI D，et al.New insights from a fixed point analysis of single cell IEEE 802.11 WLANs［C］/The 24th Annual Joint Conference of the IEEE Computer and Communications Societies，March 13-17，2005，Miami，FL，USA.New Jersey：IEEE Xplore，c2005：1550-1561.

［3］CALì F，CONTI M，GREGORI E.Dynamic tuning of the IEEE 802.11 protocol to achieve a theoretical throughput limit［J］.IEEE/ACM Transactions on Networking，2000，8（6）：785-799.

［4］WU H，PENG Y，LONG K，et al.A simple model of IEEE 802.11 wireless LAN［C］//The International Conferences on Info-tech and Info-net，October 12-14，2001，Beijing，China.New Jersey：IEEE Xplore，c2001：514-519.

［5］SAKURAI T，VU H L.MAC access delay of IEEE 802.11 DCF［J］.IEEE Transactions on Wireless Communications，2007，6（5）：1702-1710.

［6］DAI L，SUN X.A unified analysis of IEEE 802.11 DCF networks：stability，throughput，and delay［J］.IEEE Transactions on Mobile Computing，2013，12（8）：1558-1572.

［7］LEE T T，DAI L.Buffered aloha with K-exponential backoff--part I：stability and throughput analysis［J］.arXiv preprint arXiv：0907.4251，2009.

［8］WANG B，SONG F，ZHANG S D，et al.Throughput modeling analysis of IEEE 802.11 DCF mechanism in multi-hop non-saturated wireless ad-hoc networks［C］/The International Conference on Communications，Circuits and Systems，May 25-27，2008，Xiamen，China.New Jersey：IEEE Xplore，c2008：383-387.

［9］GUPTA N，RAI C S.Non-saturation throughput analysis of IEEE 802.11 DCF considering short retry limit for single hop ad hoc networks［C］/The Second International Conference on Future Generation Communication Technology（FGCT），November 12-14，2013，London，United Kingdom.New Jersey：IEEE Xplore，c2013：10-15.

［10］MALONE D，DUFFY K，LEITH D.Modeling the 802.11 distributed coordination function in nonsaturated heterogeneous conditions［J］.IEEE/ACM Transactions on Networking，2007，15（1）：159-172.

［11］ABRAMSON N.Packet switching with satellites［C］/The National Computer Conference and Exposition，June 4-8，1973，New York，USA.New York：AFIPS Press，c1973：695-702.

步超倫（1991-），男，上海交通大學碩士生，主要研究方向為無線通信網絡協議性能分析。

Performance analysis of random access network w ith post-backoff

BU Chaolun1，XIAO Yang1，YE Tong1，WU Peng2，ZHANG Xiaojian2，WU Junmin2
1.State Key Laboratory of Advanced Optical Communication Systems and Networks，Shanghai Jiaotong University，Shanghai 200240，China 2.State Grid Smart Grid Research Institute，Nanjing 210003，China

Performance analysis of random access network protocol in wireless local area network is a research hotspot in recent years，and the existing models have yet to describe post-backoff mechanism effectively.Therefore，the performance of the random access network under the unsaturated condition based on a two stage Markov model was analyzed.First of all，embedded Markov chain was used to describe the service process of the head-of-line（HOL）packet in each node，then the concept of virtual service time was introduced，namely regarding the p ost-backoff process after the successful transmission as a part of the HOL packet service time，then the virtual service time distribution of the HOL packet was attained.Next，the queuing process of each node was considered as a Geo/G/1 system，then the close-form result of system throughput，delay and the range of the stable region under the unsaturated condition was achieved.The simulation results have verified the accuracy of our model.The model will shed light on the future research on distributed coordination function（DCF）protocol in wireless local area network.

random access network，post-backoff，performance analysis，Markov chain

The Key Technology and Power Grid Application Research of All-Optic Switching

TN929.5

A

10.11959/j.issn.1000-0801.2016055

2015-08-20；

2016-01-07

全光交換關鍵技術及電網應用研究項目

吳軍民（1971-），男，國網智能電網研究院高級工程師，主要研究方向為電力系統通信。

肖揚（1992-），男，上海交通大學本科在讀，主要研究方向為無線通信網絡協議性能分析。

葉通（1976-），男，博士，上海交通大學副教授，主要研究方向為寬帶交換網絡結構、網絡算法設計和性能分析、光網絡系統。

吳鵬（1984-），男，國網智能電網研究院中級工程師，主要研究方向為電力系統通信。

張小建（1969-），男，國網智能電網研究院高級工程師，主要研究方向為電力系統通信。