電離層閃爍模型中的不均勻體強度建模

劉鈍 閆永寶 郭珊 於曉 馮健 甄衛(wèi)民

(中國電波傳播研究所,青島 266107)

?

電離層閃爍模型中的不均勻體強度建模

劉鈍 閆永寶 郭珊 於曉 馮健 甄衛(wèi)民

(中國電波傳播研究所,青島 266107)

不均勻體強度模型是電離層閃爍建模的重要組成部分. 參考國外電離層閃爍建模的思路,利用海口地區(qū)2003年至2008年的GPS閃爍觀測數(shù)據(jù)建立了中國低緯地區(qū)電離層閃爍不均勻體強度模型,并對模型精度進行了分析. 利用2003年至2008年海口地區(qū)GPS閃爍數(shù)據(jù)進行的模型精度分析表明,模型誤差為無偏正態(tài)分布,誤差方差為0.44. 利用2013年海口地區(qū)和廣州地區(qū)GPS閃爍數(shù)據(jù)進行的模型精度分析表明,模型誤差基本保持無偏的正態(tài)分布特征,誤差方差為0.42. 利用國外模型進行同樣的精度分析,其誤差均值為0.33,方差為0.99,且為有偏分布. 由此表明,建立的閃爍強度模型在中國低緯地區(qū)具有良好的適用性.

電離層閃爍;不均勻體;擾動強度;建模;全球定位系統(tǒng)

DOI 10.13443/j.cjors.2015081901

引 言

電離層閃爍是影響衛(wèi)星導(dǎo)航、對地觀測(星載合成孔徑雷達)等系統(tǒng)的重要因素. 為實現(xiàn)上述系統(tǒng)對電離層閃爍影響的分析評估,需建立電離層閃爍模型,模擬生成閃爍影響下的信號形式,并結(jié)合系統(tǒng)性能模型,開展電離層閃爍影響的分析研究工作[1-3].

電離層閃爍模型主要包括電離層不均勻體模型和信號傳播模型兩部分[2-4]. 電離層不均勻體模型對造成電離層閃爍的不均勻體特性進行建模,包括不均勻體高度、厚度、強度以及譜指數(shù)等特征參量[5-12]. 其中,不均勻體強度模型是最主要的模型. 信號傳播模型一般采用相位屏方法實現(xiàn),這是因為相位屏理論一方面是解釋閃爍現(xiàn)象的理論模型之一,另一方面,廣泛的試驗分析工作也驗證了相位屏仿真結(jié)果與實測結(jié)果具有較好的一致性[13-14]. 本文重點針對電離層閃爍模型中的不均勻體強度模型開展研究.

電離層不均勻體強度模型的建立主要有兩種思路:一種思路是直接對不均勻體強度(實際為不均勻體擾動強度與不均勻體厚度的乘積CsL或CkL)進行統(tǒng)計建模,以美國WBMOD為典型的電離層閃爍模型即采用這種思路[7-12];另一種思路是對造成不均勻體強度變化的電離層電子密度變化δNe進行建模,典型的模型包括歐洲的電離層閃爍模型GISM,以及WBMOD早期的相關(guān)工作[4-6]. 兩種方法各有優(yōu)點. 基于電離層不均勻體強度的建模中,由于可以利用地基閃爍觀測進行不均勻體強度的測量和反演,因此可以獲得大量數(shù)據(jù)進行模型的建立和測試,尤其是隨著全球?qū)Ш叫l(wèi)星系統(tǒng)(Global Navigation Satellite System,GNSS)的出現(xiàn)并用于電離層閃爍觀測,這種方法更具有實用意義[10]. 基于電離層電子密度變化實現(xiàn)的閃爍建模中,可以實現(xiàn)除閃爍相關(guān)參量外更多參量的分析研究,如信號延遲、法拉第旋轉(zhuǎn)等[4]. 但不管電離層不均勻體模型采用何種方式建立,上述電離層閃爍模型中的信號傳播模型均采用相位屏方法實現(xiàn).

本文采用對不均勻體參量CkL進行建模的方法實現(xiàn)對電離層閃爍強度的建模研究. 第二節(jié)介紹利用GPS閃爍測量數(shù)據(jù)提取電離層不均勻體強度的反演方法,和電離層閃爍強度模型的實現(xiàn)形式. 第三節(jié)利用海口地區(qū)的閃爍觀測數(shù)據(jù)對閃爍強度模型進行參量估計和實現(xiàn). 第四節(jié)進一步利用海口和廣州地區(qū)不同年份的閃爍觀測數(shù)據(jù)對建立的閃爍強度模型進行有效性分析,最后給出了結(jié)論.

1 閃爍相關(guān)的電離層不均勻體建模方法

1.1 電離層不均勻體參量

描述電離層閃爍相關(guān)不均勻體的參數(shù)包括不均勻體高度、厚度、 強度、漂移速度、軸比、譜指數(shù)等參數(shù)[8-9,12]. 其中,不均勻體強度是電離層閃爍建模應(yīng)用中最重要的參量. C.L.Rino在文獻[13]中通過相位屏理論建立了電離層幅度閃爍指數(shù)S4的表達式:

(1)

(2)

ν=p/2.

(3)

式(1)～(3)中: re為經(jīng)典電子半徑; λ為入射波波長; L為不均勻體厚度; θ為入射信號在接收機處的天頂角; Cs為擾動強度; Γ為gamma函數(shù); F為傳播幾何因子; zR=zzs/(z+zs),z和zs分別為電離層相位屏到地面接收機和衛(wèi)星的距離; p為譜指數(shù). 由于Cs與L的影響難以分離,電離層閃爍研究中,一般將CsL作為一個參量進行建模[7-8]. 文獻[12]進一步引入了新的參量CkL描述不均勻體強度,其與CsL的關(guān)系如下:

CkL=(1000/2π)p+1CsL.

(4)

由式(1)可以獲得CsL的理論公式為:

(5)

式(5)表明,可以通過實測的閃爍指數(shù),獲得相應(yīng)的電離層不均勻體強度CsL或CkL的估計. 該公式中,θ,F,Z等參數(shù)可以通過閃爍觀測中的衛(wèi)星位置、 接收機位置計算獲得. 譜指數(shù)可由閃爍原始觀測數(shù)據(jù)進行譜分析估計獲得. 低緯地區(qū)電離層閃爍分析表明,譜指數(shù)一般可取為2.5[8]. 在工作中,分別采用實測數(shù)據(jù)獲得的譜指數(shù)和采用經(jīng)驗譜指數(shù)兩種方法進行CsL提取. 統(tǒng)計分析表明,兩種方法的結(jié)果沒有明顯差別,因此數(shù)據(jù)分析中,采用取經(jīng)驗譜指數(shù)的方法進行CsL估計.

1.2 電離層不均勻體強度模型

電離層閃爍研究表明,閃爍與緯度、季節(jié)、日落后時間、太陽活動等因素有關(guān). 因此,閃爍建模中,一般通過引入上述參量的不同函數(shù)形式進行不均勻體強度的建模,如在文獻[8]中,將不均勻體強度表示為太陽黑子數(shù)R、晨昏線與磁子午線在磁赤道的夾角τ(反映季節(jié)變化)、 E層日落后時間te,以及磁不變緯度λa的函數(shù)形式,表達式為

(6)

由于CsL與CkL的定量關(guān)系,本文考慮建立

(7)

形式的不均勻體強度CkL模型,并利用實測數(shù)據(jù)對模型參數(shù)進行估計. 式(7)中:fr(R)為與太陽黑子數(shù)相關(guān)的函數(shù); fs(τ)為晨昏線與磁子午線夾角τ的函數(shù); ft(te)為E層日落后時間te的函數(shù); fλ(λa)為磁不變緯度λa的函數(shù).

上述不均勻體模型中,僅需利用實測數(shù)據(jù)對不同函數(shù)的相對變化形式進行估計建模,不同模型的絕對偏差可以被系數(shù)CE吸收,而CE最后通過最小二乘方法利用所有實測數(shù)據(jù)進行最優(yōu)估計獲得.

2 電離層不均勻體強度模型的參數(shù)估計與實現(xiàn)

利用海口地區(qū)2003年至2008年期間GPS測量的幅度閃爍指數(shù)進行電離層不均勻體強度CkL的反演提取,并進一步用于電離層閃爍不均勻體強度模型的參數(shù)估計.

2.1 fr(R)模型估計

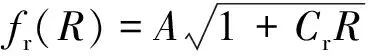
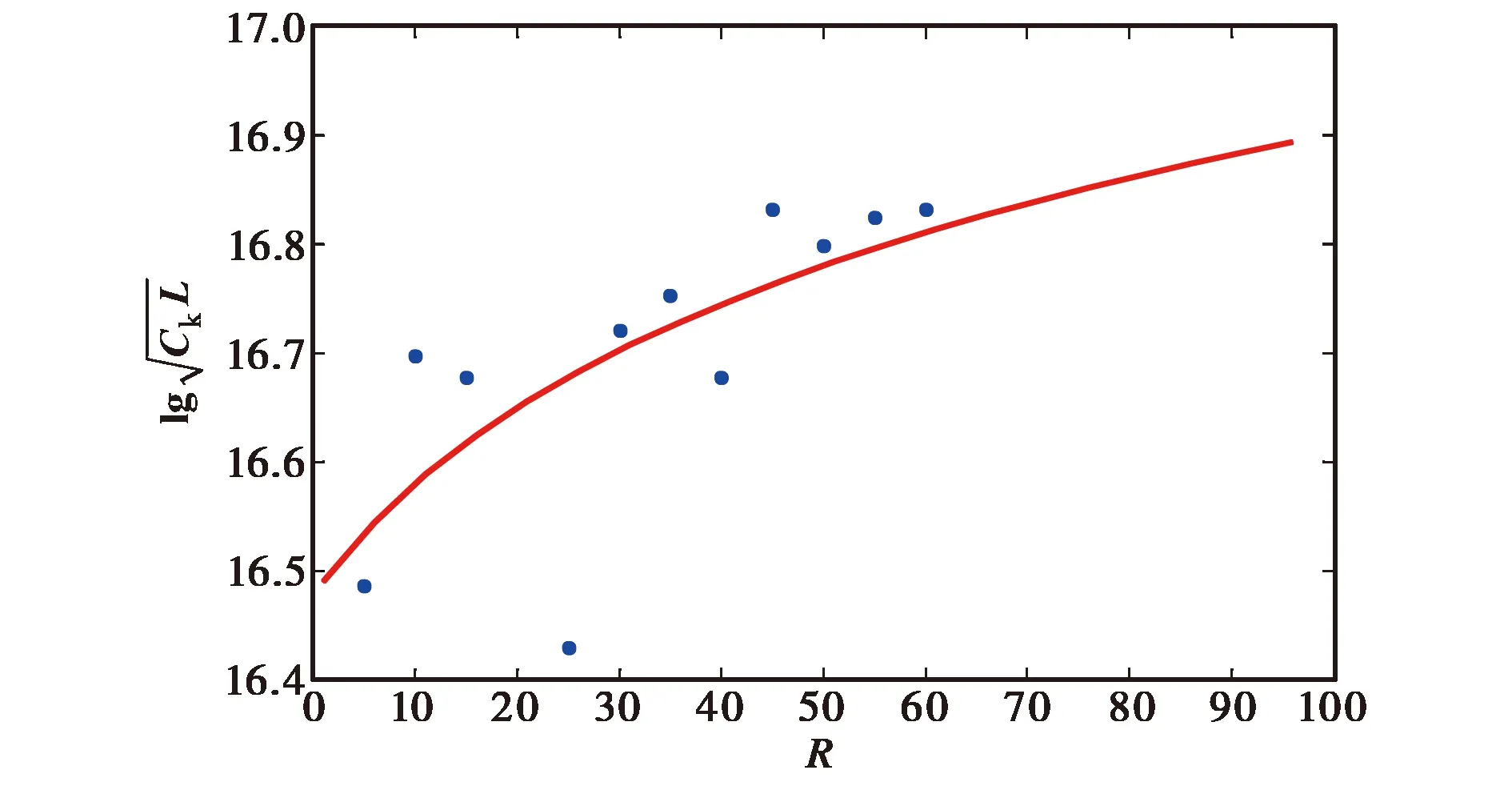
圖)對太陽黑子數(shù)R的擬合結(jié)果

2.2 fs(τ)模型估計

根據(jù)文獻[8]的結(jié)果,fs(τ)取如下函數(shù)形式:

(8)

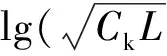
2.3 ft(te)模型估計

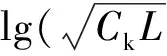
(9)

圖對E層日落后時間te的擬合結(jié)果

2.4 fλ(λa)模型估計

電離層閃爍建模中不均勻體強度隨磁不變緯度的變化較為復(fù)雜. 文獻[5-8]的模型實現(xiàn)中,電離層不均勻體強度在整個磁低緯地區(qū)隨磁不變緯度具有同樣變化,而在磁低緯與中緯交界處,以誤差函數(shù)形式進行過渡,文獻[9,11]則建立了具有雙峰值的電離層不均勻體強度隨磁不變緯度變化的函數(shù)形式. 由于海口地區(qū)閃爍觀測的覆蓋范圍有限,建模工作中采取文獻[8]中給出的fλ(λa)函數(shù)形式:

(10)

fs(τ)ft(te)))隨磁不變緯度λa的變化分布及fλ(λa)函數(shù)的擬合結(jié)果,表明了采用該函數(shù)模型的有效性.

圖對磁不變緯度λa的擬合結(jié)果

將估計的fr(R)、fs(τ)、ft(te)、fλ(λa)等函數(shù)代入公式(7),并利用最小二乘方法由所有原始數(shù)據(jù)估計CE,最后可以獲得電離層不均勻體強度CkL的估計模型.

3 電離層不均勻體強度模型有效性評估

為了驗證建立的電離層閃爍不均勻體強度模型的有效性,利用海口、廣州區(qū)域的GPS電離層閃爍觀測數(shù)據(jù)對模型精度進行分析驗證.

利用GPS衛(wèi)星位置、觀測站位置以及觀測時間,計算電離層不均勻體強度模型所需的參數(shù),并帶入模型獲得相應(yīng)時間、地點的電離層不均勻體強度估計. 對所有閃爍觀測數(shù)據(jù)進行處理,獲得對應(yīng)時間、地點的不均勻體強度估計,并與實測的不均勻體強度數(shù)據(jù)進行比較,通過對實測數(shù)據(jù)與模型估計數(shù)據(jù)的誤差統(tǒng)計分析,獲得電離層不均勻體強度模型的精度分析結(jié)果.

3.1 利用海口2003-2008年數(shù)據(jù)的驗證結(jié)果

由于本文中的電離層不均勻體強度模型利用2003-2008年海口地區(qū)的閃爍觀測數(shù)據(jù)建立,因此,利用海口地區(qū)2003-2008年數(shù)據(jù)進行的驗證主要是分析建立的電離層不均勻體強度模型的內(nèi)符精度. 圖5給出了比較的結(jié)果,其中紅線為擬合的正態(tài)分布(下同). 可以看出. 電離層不均勻體強度模型的誤差呈正態(tài)分布,誤差均值為0,方差為0.44.

進一步利用同樣的實測數(shù)據(jù)(海口地區(qū)2003—2008年GPS閃爍觀測數(shù)據(jù))對文獻[8]中給出的WBMOD模型進行精度分析,圖6給出了模型的誤差分布,其中誤差均值為0.33,方差為0.99. 可以看出,該閃爍強度模型的估計存在系統(tǒng)性偏差,且誤差的方差分布是本文建立模型的2倍以上.

圖5 利用海口地區(qū)2003-2008年數(shù)據(jù)對建立的閃爍強度模型的分析結(jié)果(誤差均值為0.00,方差為0.44)

圖6 利用海口地區(qū)2003-2008年數(shù)據(jù)對文獻[8]中閃爍強度模型的分析結(jié)果(誤差均值為0.33,方差為0.99)

實際應(yīng)用中,不僅希望獲得不均勻體強度的大小估計,還希望獲得不均勻體強度的發(fā)生概率估計. 實現(xiàn)模型的誤差為無偏正態(tài)分布且具有較小方差,這一特征表明,利用該模型可以實現(xiàn)給定置信度下的閃爍強度估計,并且誤差更小,這對于實際應(yīng)用具有重要意義.

3.2 利用海口、 廣州2013年數(shù)據(jù)的驗證結(jié)果

為了進一步驗證建立的閃爍不均勻體強度模型的有效性,利用海口地區(qū)和廣州地區(qū)的GPS閃爍數(shù)據(jù)對模型的精度進行分析.

圖7給出了利用海口地區(qū)2013年全年GPS閃爍觀測數(shù)據(jù)對建立的閃爍不均勻體強度模型的精度分析結(jié)果.其中,模型誤差均值為0.07,方差為0.42. 圖8給出了利用廣州地區(qū)2013年下半年GPS閃爍觀測數(shù)據(jù)進行的模型精度分析結(jié)果. 其中,模型誤差均值為0.01,方差為0.42.

圖7 利用海口地區(qū)2013年數(shù)據(jù)對建立的閃爍強度模型的分析結(jié)果(誤差均值為0.07,方差為0.42)

圖8 利用廣州地區(qū)2013年下半年數(shù)據(jù)對建立的閃爍強度模型的分析結(jié)果(誤差均值為0.01,方差為0.42)

可以看出,建立的閃爍不均勻體強度模型在海口和廣州區(qū)域,在更高太陽活動年份(2013年)情況下,仍具有良好的精度. 兩種情況下,模型誤差基本保持無偏的正態(tài)分布特征,誤差方差為0.42,與海口地區(qū)2003-2008年數(shù)據(jù)的比較結(jié)果具有很好的一致性.

上述分析結(jié)果表明,本文建立的電離層閃爍不均勻體強度模型在中國低緯地區(qū)具有良好的適用性.

需要說明的是,與2003—2008年的GPS閃爍觀測相比,2013年的GPS觀測數(shù)據(jù)中受干擾影響現(xiàn)象較為嚴(yán)重(尤其是射頻干擾和多徑影響),因此有效閃爍事件識別和數(shù)據(jù)處理的難度進一步加大,容易造成個別“壞”數(shù)據(jù)沒有被閃爍數(shù)據(jù)批處理和質(zhì)量檢測程序識別和剔除. 這也是造成2013年模型精度分析中,誤差分布存在較小偏差的原因.

4 分析與結(jié)論

電離層不均勻體強度模型是電離層閃爍建模的重要組成部分. 參考國外電離層閃爍建模的思路,利用海口地區(qū)2003年至2008年的GPS閃爍觀測數(shù)據(jù)建立了中國低緯地區(qū)的電離層閃爍不均勻體強度模型,并對模型的精度進行了分析.

利用2003年至2008年海口地區(qū)GPS閃爍數(shù)據(jù)進行的模型內(nèi)符精度分析表明,模型誤差為無偏正態(tài)分布,誤差方差為0.44. 利用國外相同模型進行同樣的精度分析,其誤差均值為0.33,方差為0.99,且為有偏分布. 利用2013年海口地區(qū)和廣州地區(qū)GPS閃爍數(shù)據(jù)進行的模型精度分析表明,建立的不均勻體強度模型其誤差基本保持無偏的正態(tài)分布特征,誤差方差與海口地區(qū)2003—2008年數(shù)據(jù)的比較結(jié)果具有一致性. 由此表明,建立的閃爍不均勻體強度模型在中國低緯地區(qū)具有良好的適用性.

觀測環(huán)境影響(主要為射頻干擾或多徑影響)是造成GPS閃爍觀測質(zhì)量降低的重要因素,將會影響閃爍強度模型的建立和驗證. 因此在電離層閃爍分析和建模中,應(yīng)建立有效的閃爍事件識別和數(shù)據(jù)處理機制與方法,降低這些因素的影響.

利用中國地區(qū)電離層閃爍觀測數(shù)據(jù)對閃爍強度模型進行完善是下一步擬開展的工作,同時,進一步完善閃爍事件的有效識別和無效數(shù)據(jù)剔除方法也是下一步的工作.

[1] 劉思慧, 劉鈍. 電離層閃爍對北斗增強系統(tǒng)影響的建模研究[J]. 電波科學(xué)學(xué)報, 2015, 30(1): 135-140.

LIU S H, LIU D. Modeling the effects of ionospheric scintillation on BD augmentation system[J]. Chinese journal of radio science, 2015, 30(1): 135-140. (in Chinese)

[2] HEGARTY C, EL-ARINI M B, KIM T, et al. Scintillation modeling for GPS/WAAS receivers[C]//Proceedings of the 1999 National Technical Meeting of The Institute of Navigation, San Diego, CA, January 25-27, 1999: 799-807.

[3] CARRANO C S, GROVES K M, CATON R G. A phase screen simulator for predicting the impact of small-scale ionospheric structure on SAR image formation and interferometry[C]//2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Honolulu, 25-30 July, IEEE, 2010: 162-165.

[4] BENIGUEL Y. GIM: A global ionospheric propagation model for scintillation of transmitted signals[J]. Radio science, 2002, 37(3), 1032-1044.

[5] FREMOUW E J, BATES H F. Worldwide behavior of average VHF-UHF scintillation[J]. Radio science, 1971, 6(10): 863-869.

[6] FREMOUW E J, RINO C L. An empirical model for average F-layer scintillation at VHF/UHF[J]. Radio science,1973, 8(3): 213-222.

[7] FREMOUW E J, SECAN J A. Modeling and scientific application of scintillation results[J]. Radio science, 1984, 10(3): 687-694.

[8] EDWARD J. FREMOUW E J, ROBINS R E. An equatorial scintillation model[R]. Bellevue: Physical dynamics Inc., 1985.

[9] SECAN J A, MUSSEY M, FREMOUW E J, et al. An improved model of equatorial scintillation[J]. Radio science, 1995, 30(3): 607-617.

[10]CERVERA M A, THOMAS R M, GROVES K M, et al. Validation of WBMOD in the southeast Asia region[J]. Radio science, 2001, 36(6): 1559-1572.

[11]SECAN J A, BUSSEY R M, FREMOUW E J. An investigation of methods for improving models of ionospheric plasma-density irregularities and radio-frequency scintillation[R]. Bellevue: Northwest Research Associates Inc. March 1993.

[12]ROBINS R E, SECAN J A，F(xiàn)REMOUW E J. A mid-latitude scintillation model[R]. Bellevue: Northwest Research Associates Inc., October 1986.

[13]RINO C L. A Power law phase screen model for ionospheric scintillation 1.weak scatter[J]. Radio science, 1979, 14(6): 1135-1145.

[14]RINO C L, FREMOUW E J. The angle dependence of singly scattered wavefields[J]. Journal of atmospheric & terrestrial physics, 1977, 39(8): 859-868.

[15]VANZANDT T E, CLARK W L, WARNOCK J M. Magnetic apex coordinates: a magnetic coordinates system for the ionospheric F2 layer[J]. Journal of geophysical research, 1972, 77(13): 2406-2411.

[16]YEH C K, LIU C H. Radio wave scintillations in the ionosphere[J]. Proceedings of IEEE, 1982, 70(4): 324-360.

[17]張光澄. 非線性最優(yōu)化計算方法[M]. 北京:高等教育出版社, 2005.

ZHANG G C. Computational methods for nonlinear optimization[M]. Beijing: Higher Education Press, 2005. (in Chinese)

劉鈍 (1973-),男,河北人,中國電波傳播研究所高級工程師,主要研究方向為電波傳播應(yīng)用技術(shù)、GNSS應(yīng)用技術(shù)研究.

閆永寶 (1986-)，男，甘肅人，博士，助理研究員，畢業(yè)于裝甲兵工程學(xué)院，主要研究方向為電波環(huán)境建模及應(yīng)用技術(shù)研究.

郭珊 (1981-),女,河南人,中國電波傳播研究所工程師,主要研究方向為GNSS電波環(huán)境監(jiān)測技術(shù)與數(shù)據(jù)處理技術(shù).

於曉 (1982-),女,湖北人,中國電波傳播研究所工程師,主要研究方向為電離層閃爍建模技術(shù)研究.

Irregularity strength modeling in ionospheric scintillation model

LIU Dun YAN Yongbao GUO Shan YU Xiao FENG Jian ZHEN Weimin

(China Research Institute of Radiowave Propagation, Qingdao 266107, China)

Disturbance strength modeling of scintillation-producing irregularity is one of the main tasks in ionospheric scintillation models. A strength model for ionospheic irregularity is constructed with GPS scintillation data from Haikou China with relating foreign models as reference. The validity of the model is also checked with extensive data. The residual of model shows unbiased distribution with mean of zero and standard deviation 0.44 for the test data of Haikou from 2003 to 2008. More test with data from Haikou and Guangzhou in 2013 also show an unbiased distribution almost with standard deviation of 0.42. On the contrary, a biased result is obtained for the models constructed in the

with a mean of 0.33 and standard deviation 0.99 when the same Haikou data set is used. The test results show the validity of the scintillation irregularity model established in the work.

ionospheric scintillation; irregularity; disturbance strength; model; GPS

10.13443/j.cjors.2015081901

2015-08-19

P352

A

1005-0388(2016)03-0432-06

劉鈍, 閆永寶, 郭珊, 等.電離層閃爍模型中的不均勻體強度建模[J].電波科學(xué)學(xué)報,2016,31(3):432-437.

LIU D, YAN Y B, GUO S, et al. Irregularity strength modeling in ionospheric scintillation model[J]. Chinese journal of radio science,2016,31(3):432-437.(in Chinese). DOI:10.13443/j.cjors.2015081901

聯(lián)系人： 劉鈍 E-mail: dun.l@163.com