丹紅注射液對比丹參注射液治療冠心病有效性及安全性的Meta分析*
王 靜 陳伶利 李義偉 鄒吉濤 杜 丹張曉維 李 鑫 王建國△ 李 杰 △
(1.湖南中醫藥大學,湖南 長沙 410208;2.中醫診斷學湖南省重點實驗室,湖南 長沙 401208)
冠心病(CHD)是冠狀動脈血管粥樣硬化性心臟疾病,臨床癥狀主要為心前區突發的發作性絞痛或壓榨痛[1]。中醫將其歸于“胸痹”范疇,機體正氣不足,恰逢外邪侵襲,氣滯、血瘀、痰濕、寒凝痹阻心脈,血行不暢郁遏而痛,故以活血化瘀為基本治療原則[2]。丹參注射液與丹紅注射液都是臨床治療CHD的常用注射液。丹參注射液具有活血化瘀,養心通絡之效,主要有效成分是丹參提取物。丹紅注射液具有活血化瘀,通脈舒絡之功,主要成分為丹參和紅花提取物。臨床治療CHD時,常常出現兩者隨意混雜使用或聯合使用的現象,不僅易產生不良反應,而且不符合藥物經濟學要求。因此,本項目首次從臨床應用層次,采用國際通用的循證醫學方法,對丹參注射液和丹紅注射液的臨床療效及安全性進行Meta分析,旨在明確兩者的適用范圍和主治病證,進而降低不良反應發生率和治療成本,以期為臨床用藥提供循證證據。
1 資料與方法
1.1 文獻選擇
1)納入標準。研究類型:丹參注射液對比丹紅注射液治療CHD的隨機對照試驗(RCTs),分為試驗組和對照組;研究對象:符合西醫診斷的冠心病心絞痛或中醫診斷的胸痹病例,不限性別、年齡;干預措施:試驗組采用丹紅注射液治療,對照組采用丹參注射液治療,均可聯合常規西藥治療。結局標準:臨床有效率、心電圖有效率、不良反應發生率、心電圖療效比較、住院時長、心肌耗氧量、心絞痛發作情況。2)診斷標準。符合中華醫學會關于CHD診斷標準、《實用內科學》《缺血性心臟病的命名及診斷標準》《第一屆全國內科學術會議關于冠狀動脈性心臟病命名及診斷標準》《1979年WTO冠心病診斷標準》。3)排除標準。綜述、動物、細胞等非臨床研究文獻;臨床個案報道;內容與主題無關、不完整或部分數據缺失;文章內容重復。
1.2 文獻檢索策略
計算機檢索 Wanfang、VIP、CNKI、PubMed 及 Cochrance Library數據庫所有關于丹紅注射液與丹參注射液治療CHD的RCTs,不限語言和國籍,同時結合手工檢索,避免漏檢,檢索日期建庫至2021年9月5日截止。中文數據庫檢索詞:“丹參注射液”“丹紅注射液”“冠心病”或“冠心病心絞痛”“心絞痛”或“胸痹”“對照”或“隨機對照”。基本檢索式:#1(丹參注射液)AND#2(丹紅注射液)AND#3(冠心病或冠心病心絞痛或心絞痛或胸痹)AND#4(隨機對照試驗或對照或對比或臨床觀察)。英文數據庫檢索詞:“Danshen Injection”“Danhong Injection”“Coronary Heart Disease”“Angina”OR“Chest Bi”“Controlled”OR“Randomized controlled”。基本檢索式:#1(Danshen Injection)AND#2(Danhong Injection)AND#3(Coronary Heart Disease OR Angina OR Chest Bi)AND#4(Randomized controlled Trials OR Contrast OR Compare OR Clinical Observation)。
1.3 評價方法
1.3.1 文獻篩選 根據納入與排除標準進行文獻篩選,使用Excel表格進行整理,提取資料的內容包括作者姓名、文獻發表年份、納入患者的病例總數及一般特征、分組方法、治療措施、結局指標、診斷標準、療效評定標準等。
1.3.2 文獻質量評價 納入研究的方法學質量按Cochrane協作網的風險偏倚評估工具進行評價:隨機分配方法應用;隨機隱藏實施;研究對象、治療方案實施者盲法實施;結果測量者盲法實施;結果數據完整性;選擇性報告;其他偏倚。
1.4 統計學處理
采用Cochrane協作網提供的Review Manager 5.3進行Meta分析。二分類結局指標效應值用相對危險度(RR)表示;計量資料用均數差(MD)或標準均數差(SMD),各效應量均以95%可信區間(95%CI)表示。采用χ2檢驗對試驗結果進行檢驗,若異質性檢驗結果顯示異質性小(I2≤50%),采用固定效應模型;若研究間異質性較大(I2>50%),使用隨機效應模型進行分析。Meta分析檢驗水準為P=0.05。
2 結果
2.1 文獻檢索結果
初步檢索出文獻共122篇,其中中國知網48篇,萬方50篇,維普24篇,按照文獻納入和排出標準最終納入文獻26篇,見圖1。

圖1 文獻篩選流程圖
2.2 納入研究的基本特征
納入26項RCTs,共2 916例,丹紅組給予丹紅注射液,丹參組給予丹參注射液;20項研究提及使用常規西藥治療[3-22],另外6 項研究則沒有提及[23-28]。具體文獻特征見表1。
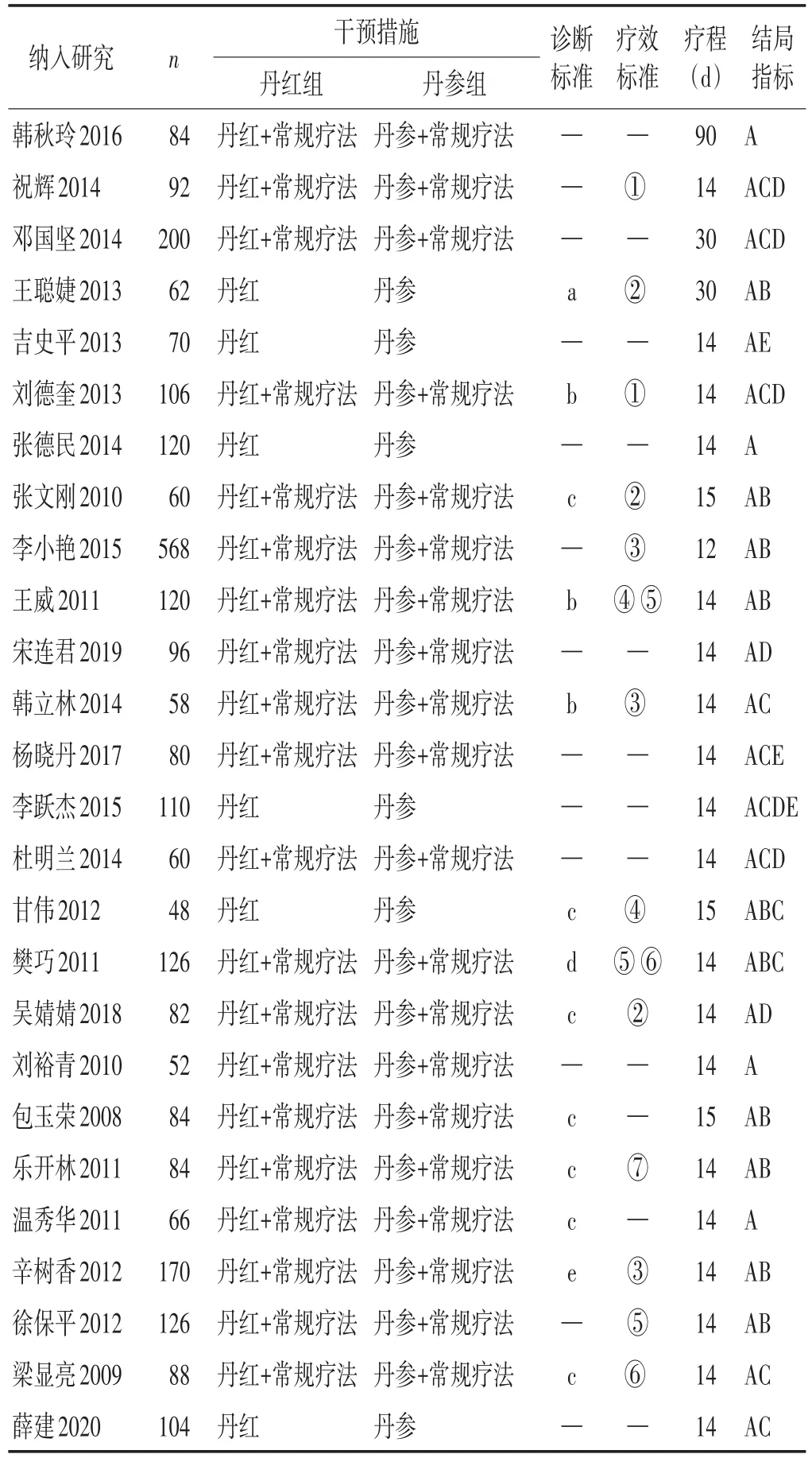
表1 納入文獻特征表
2.3 納入研究質量評價
26項RCTs中2項明確隨機分組方法[15,22],4項未提 及[11-12,18,28],20項提及但未具體[3-10,13-14,16-17,19-21,23-27]。26 項研究均未提及分配隱藏、其他偏倚及盲法,均未提前終止試驗,見圖2。
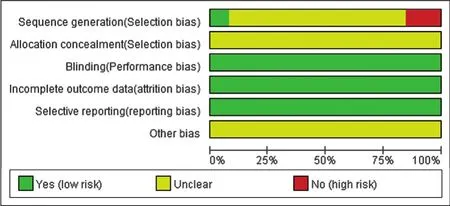
圖2 偏倚風險評價
2.4 Meta分析
2.4.1 臨床療效 26項RCTs均報道臨床有效率,具有同質性(χ2=26.75,P=0.37,I2=7%),采用固定效應模型分析。Meta分析顯示,RR=1.25,95%CI[1.21,1.29],Z=13.54,P<0.00001,差異有統計學意義,見圖3。

圖3 臨床有效率
根據不同的診斷標準,將使用頻次≥3次的診斷標準進行亞組型分析。合并分析總異質性,P=1.00,I2=0%;各組間無異質性,采用固定效應模型。3項參照《實用內科學》,P=0.59,I2=0%;RR=1.29,95%CI[1.16,1.44],差異無統計學意義。7項參照《缺血性心臟病的命名及診斷標準》,P=1.00,I2=0%;RR=1.30,95%CI[1.19,1.40],差異無統計學意義。綜上,兩組亞組差異無統計學意義,丹紅注射液與丹參注射液的臨床有效率與診斷標準無關,見圖4。

圖4 臨床有效率診斷標準的亞組型分析
按照不同的療效評定標準,將使用頻次≥3次的療效評定標準進行亞組型分析。合并分析總異質性,P=0.66,I2=0%,各組間無異質性,采用固定效應模型。3項參照《冠心病診療指南》,P=1.00,I2=0%;RR=1.27,95%CI[1.11,1.44],差異無統計學意義。3項參照《中國常見心腦血管疾病診治指南》,P=0.26,I2=26%;RR=1.27,95%CI[1.19,1.36],有顯著性差異。3項《冠心病及心電圖療效評定標準》,P=0.23,I2=31%;RR=1.24,95%CI[1.13,1.37],差異有統計學意義。綜上,3組亞組分析的總差異無統計學意義,丹紅注射液與丹參注射液的臨床療效有效率與其療效評定標準無關,見圖5。

圖5 臨床有效率評定標準的亞組型分析
2.4.2 心電圖評價 1)二分類變量。10項RCTs在結局指標中報道心電圖有效率,具有統計學同質性,采用固定效應模型分析(χ2=3.03,P=0.93,I2=0%)。Meta分析顯示,RR=1.26,95%CI[1.18,1.35],Z=6.74,P<0.00001,有統計學差異。結果顯示丹紅注射液對比丹參注射液的心電圖有效率更高,見圖6。
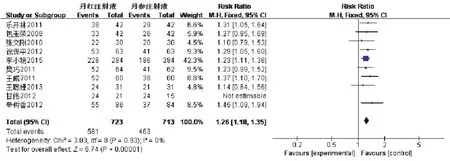
圖6 心電圖有效率
根據不同的診斷標準,將使用頻次≥3次的診斷標準進行亞組型分析。4項參照《缺血性心臟病的命名及診斷標準》,合并分析總異質性,P=0.78,I2=0%;RR=1.27,95%CI[1.10,1.46],具有同質性,采用固定效應模型。結果顯示亞組分析無統計學意義,丹紅注射液與丹參注射液的心電圖有效率與診斷標準無關,見圖7。
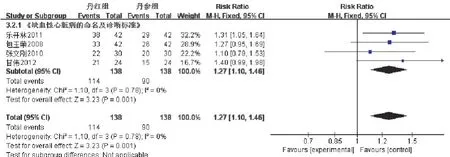
圖7 心電圖有效率不同診斷標準的亞組型分析
根據不同的療效評定標準,將使用頻次≥3次的療效評定標準進行亞組型分析。3項參照《冠心病及心電圖療效評定標準》,合并分析總異質性,P=0.79,I2=0%,有同質性,采用固定效應模型。RR=1.29,95%CI[1.14,1.46]。亞組分析差異無統計學意義,丹紅注射液與丹參注射液的臨床有效率與療效評定標準無關,見圖8。

圖8 心電圖有效率評定標準的亞組型分析
2)連續變量。7項RCTs報道心電圖治療效果有異質性,采用隨機效應模型分析(χ2=77.08,P<0.00001,I2=92%)。結果顯示,MD=-0.27,95%CI[-0.80,0.26],Z=1.01,P=0.31,有統計學意義,提示丹紅注射液心電圖療效比丹參注射液好,見圖9。
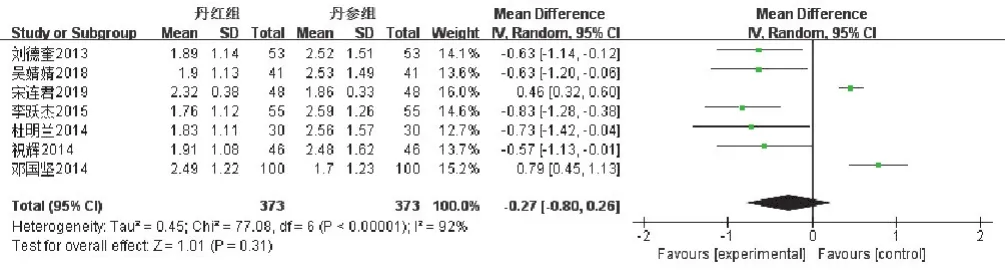
圖9 心電圖療效比較
2.4.3 住院時長 3項RCTs報道住院時長,有統計學異質性,采用固定效應模型分析(χ2=3.44,P=0.18,I2=42%)。分析表明,MD=-5.81,95%CI[-6.40,-5.23],Z=19.61,P<0.00001,有統計學意義。結果顯示使用丹紅注射液住院時長更短,見圖10。

圖10 住院時長
2.4.4 不良反應率 10項研究報道了不良反應,有統計學同質性,采用固定效應模型分析(χ2=3.53,P=0.97,I2=0%)。Meta分析顯示,RR=0.65,95%CI[0.40,1.05],Z=1.77,P=0.08,差異無統計學意義。因此使用丹紅注射液和丹參注射液對不良反應的發生無差異,見圖11。

圖11 不良反應發生率
2.5 發表偏倚評估
RCTs納入文獻大于10篇的研究結果做漏斗圖分析,臨床有效率、心電圖有效率、不良反應發生率的漏斗圖均未見顯著不對稱,提示發表偏倚較小,系統評價結果可信度較高,見圖12。
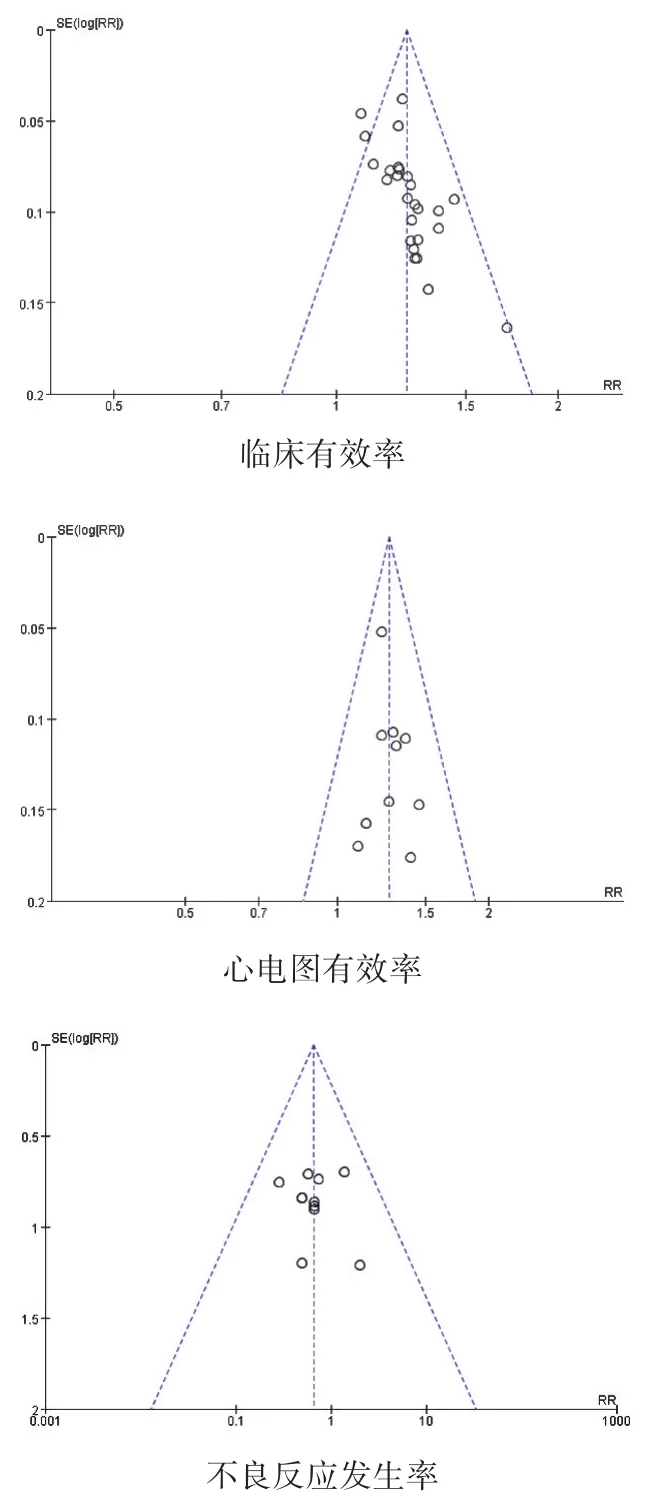
圖12 發表偏倚分析
2.6 敏感性分析
選擇改變效應模型觀察RR和MD變化的方法評估本次Meta分析的敏感性。本次Meta分析穩定性較好,除心電圖療效改變效應模型后變化較大,其余指標敏感性較低,RCTs結果可信,見表2。
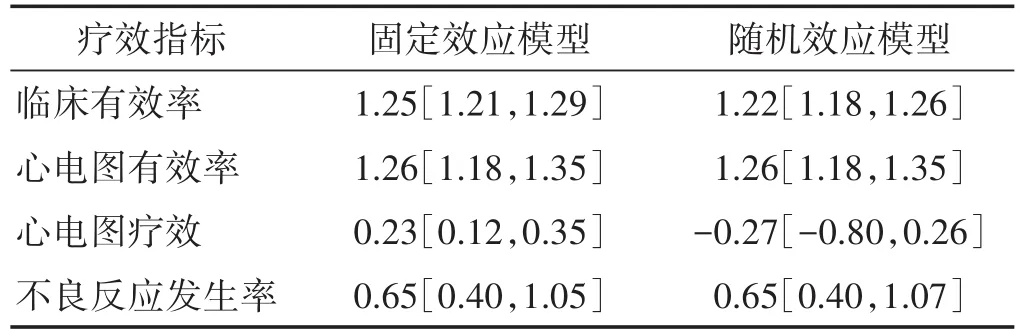
表2 敏感性分析
3 討 論
丹參注射液與丹紅注射液都是療效確切的CHD臨床治療藥物。丹參和紅花均具活血化瘀之功效,常相須為用協同增效。本次RCTs納入26項研究,共2 916例。通過Meta綜合分析各結局指標,臨床有效率綜合臨床癥狀改善情況與實驗室檢查結果[5],提示丹紅注射液在提高CHD患者臨床療效方面優于丹參注射液,丹紅注射液可明顯改善CHD患者臨床主要癥狀及實驗室檢查結果。心電圖有效率指ST段及T波恢復情況[8],心電圖療效指ST段壓低導聯數變化[4],提示丹紅注射液對患者心電圖的改善優于丹參注射液。住院時長用于衡量患者治療后的恢復情況,使用丹紅注射液者住院時間更短,提示丹紅注射液可加快患者康復時間。
本研究的不足在于丹參注射液與丹紅注射液均屬于中藥注射液,但診斷并未按照中醫證型辨證,可能會造成一定的偏倚。
綜上,當前Meta分析結果表明,丹紅注射液治療CHD的臨床療效較丹參注射液好,且不良反應發生率較低。建議今后開展丹紅注射液或丹參注射液的臨床研究時,設計規范、嚴謹的高質量研究方案,以提供更全面、科學、客觀的臨床治療證據。

