基于相位補償法和粒子群算法的PSS4B參數優化方法*

沈　鑫，馬紅升，李仕林，王　昕，劉清蟬

（云南電網有限責任公司電力科學研究院，昆明650217）

基于相位補償法和粒子群算法的PSS4B參數優化方法*

沈鑫*，馬紅升，李仕林，王昕，劉清蟬

（云南電網有限責任公司電力科學研究院，昆明650217）

隨著電網規模越來越大，電力系統低頻振蕩問題日益突出。電力系統穩定器是解決低頻振蕩的有效措施之一，針對目前使用的PSS存在一些不足，對寬頻段的電力系統穩定器進行了研究，并采用基于相位補償法和粒子群優化算法對寬頻段電力系統穩定器的模型參數進行優化，通過RTDS仿真和現場實測，說明優化后的PSS4B能夠滿足不同寬頻段的要求，有效抑制低頻振蕩。

電力系統穩定器；相位補償法；粒子群算法；寬頻段；參數優化

隨著高增益快速勵磁系統的廣泛應用和大系統之間的弱互聯，系統對振蕩的阻尼作用將會減弱，從而在小擾動作用下容易引發低頻振蕩，限制了互聯系統間的功率傳輸。勵磁系統的附加電力系統穩定器PSS（Power System Stabilizer）控制可以有效抑制低頻振蕩的發生，改善電力系統運行的安全性和經濟性［1］。全國聯網工程的研究表明，我國區域電網之間存在0.1 Hz～0.3 Hz的低頻振蕩模式，在沒有配置PSS的情況下，成為負阻尼振蕩模式。

目前，PSS仍然是抑制電力系統低頻振蕩、提高系統穩定性的首選措施，但是新的電網發展形勢對于現有的PSS提出了新的要求：需要有更寬的工作頻域。現在我國廣泛采用的PSS2A/B以合成加速功率作為輸入信號，有效克服了“無功反調”現象，但其為單分支結構，增益特性隨頻率單調遞增，高頻段和低頻段增益差距顯著往往難以兼顧，特別是PSS2A/B的兩級隔直環節導致0.2 Hz附近的低頻段總提供較大的相位領先，限制了穩定器可提供的正阻尼，有時甚至提供負阻尼。

為了滿足現代電力系統的需求，一種多頻段電力系統穩定器PSS4B應運而生。PSS4B在2000年由加拿大魁北克電力局提出，適合加拿大電網分省管理、跨國送電的復雜的形式，目前國內只有華北電科院聯合ABB在現場作了適應性檢測，并無實際工程應用。PSS4B模型是在PSS2A/B模型的基礎上加以改進形成，其最大特點在于將轉速/功率信號分為低頻、中頻及高頻3個頻段，分別對應低頻振蕩范圍的各頻段，可在更大的頻率范圍內提供更好的靈活性來實現更優的抑制振蕩阻尼性能。現有的對于PSS4B模型［2］及其改進模型［6-10］的理論研究已經較為成熟，但是針對相應參數整定研究并未深入，往往采用典型參數使得眾多參數的靈活性并未得到充分利用。本文提出一種基于相位補償法和粒子群優化算法的PSS4B參數優化方法，根據單機無窮大系統中機組勵磁控制系統滯后特性，通過補償實現了整個寬頻段范圍內補償誤差最小，并且幅頻特性能夠同時兼顧高低頻段，最后通過RTDS進行了試驗仿真驗證。

1　相位補償法優化PSS

1.1基于單機無窮大系統的無補償頻率特性計算

勵磁控制系統滯后特性即無補償頻率特性，是指附加力矩對于PSS迭加點的滯后角度，是PSS參數優化的基礎。目前對于無補償頻率特性的獲取多通過公式計算，即利用發電機數據和發電機出口到無窮大系統的等值電抗值，通過線性化Heffron-Philips模型計算。對于遠離負荷中心的發電機，可以將發電機以外的系統等值為一個單機無窮大系統，系統包含系統電抗Xs=XL+XT和無窮大母線Vs，如圖1所示。

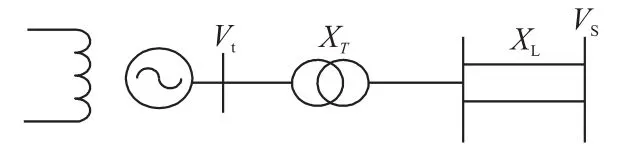
圖1　單機無窮大系統

單機無窮大系統Phillips-Heffron模型的傳遞函數如圖2所示。

圖2　單機無窮大系統線性化Phillips-Heffron模型

由圖2可知，無補償頻率特性即為ΔEq′/ΔUpss的頻率特性，ΔUpss為PSS輸出的控制信號，無補償頻率特性的計算范圍按照PSS4B補償要求設置為0.04 Hz～4.00 Hz。

1.2相位補償法基本原理

相位補償法［11］是PSS參數整定的經典方法之一，具有適應范圍廣、魯棒性強的優點。圖2中發電機機械環節就是發電機轉子運動的線性化方程，機械環節以外的部分對電磁轉矩貢獻記作ΔMe2。由圖2可知

式中，Mdelta（s）和Mpss（s）分別為從Δδ和ΔUpss到ΔMe2的前向通道的傳遞函數。轉矩分析就是將ΔMe2在Δω-Δδ坐標上分解為阻尼轉矩（與Δω成正比）和同步轉矩（與Δδ成正比），即

式中，Cdelta和Cpss為同步轉矩系數；Ddelta和Dpss為阻尼轉矩系數。若PSS的傳遞函數為Gpss（s），輸入信號為Δω，相位補償設計PSS就是整定PSS參數，使得在整個低頻振蕩范圍內PSS輸出的力矩向量對應Δω軸超前不大于10o、滯后不大于45o（即在-80o～-135o有補償特性），盡可能在不影響同步轉矩的情況下提供更大的阻尼轉矩［2，19-20］，即

ωs為系統低頻振蕩角頻率，即

不同運行方式下系統振蕩模式不同，一般采用智能算法來尋求一組PSS參數，使其同時補償整個頻段上的勵磁系統相位滯后，從而為各種運行方式都提供最大的阻尼轉矩。本文將采用文獻［14］介紹的PSO算法并對其進行適當改進，采用該優化算法可以在限定的參數范圍內尋找目標函數的最優解。PSO算法的特點在于收斂速度較快、算法簡單、容易編程實現，雖然提供全局搜索的可能，但是并不能保證搜索到全局最優點。綜合考慮，為了平衡粒子群算法的全局搜索能力和改良局部能力，自適應地改變慣性權重ω，如式（5）所示。即當各微粒的目標值趨于一致或者趨于局部最優時，將使慣性權重增加；而各微粒的目標值比較分散時，將使慣性權重減小。同時對于目標函數值優于平均目標值的微粒，其對應的慣性權重因子減小，從而保護了該微粒；反之對于目標函數值差于平均目標值的微粒，其對應的慣性權重因子較大，使得該微粒向較好的搜索區域靠攏。

式中，ωmax，ωmin分別為慣性權重的極值，J，Javg，Jmin分別為微粒目標函數，目標函數平均值以及最小值。

2　PSS4B參數優化

2.1PSS4B模型及參數分析

PSS4B的數學模型如圖3所示，以發電機轉子轉速/有功功率為輸入信號，通過信號采集傳感器作用，將輸入信號分離為低頻、中頻和高頻3個頻段。每個頻段都由正、負兩個分支組成，每個分支又由增益模塊、中心濾波環節和兩個標準的超前滯后模塊組成。從結構上看，相對于之前出現的穩定器，PSS4B主要具有以下兩個優點［2］：

（1）雙偷入之前傳統的PSS2A，僅采用了單一輸入信號，可能會出現較嚴重的“反調”現象。而PSS4B則綜合了發電機轉子轉速和有功功率兩種輸入信號，可以避免有功功率快速變化時而引起的無功功率波動，較好地消除“反調”現象。

（2）多頻段PSS4B又稱為多頻段穩定器，具有3個頻段，每個都可以單獨調節增益、濾波器、補償相位、輸出限幅等環節參數，可以為不同的振蕩模式提供合適的阻尼。其頻段按照低頻振蕩范圍劃分為低、中、高三段。低頻段（0.04 Hz～0.10 Hz）主要針對電力系統的全局模式設計；中頻段（0.1 Hz～1.0 Hz）主要針對區域間振蕩模式設計；高頻段（1 Hz～4 Hz）主要針對局部振蕩模式或廠站機組間的低頻振蕩模式而設計。顯然，僅用一臺PSS4B就可以對多個振蕩模式產生良好的抑制效果。而之前出現的穩定器均只有一個頻段，高頻段和低頻段難以兼顧［7］。

對于PSS4B的參數，雖然表面上看起來很繁瑣復雜，但實際上常用一種簡便的參數設置方法，即把PSS4B的3個頻段設置成對稱的帶通濾波器形式，各頻段濾波器在中心頻率處增益最大，且相位為零，便于進行超前滯后計算。實際工程中，還需要根據發電機組及其在系統中的位置進行現場調試設置工作［2-5］。

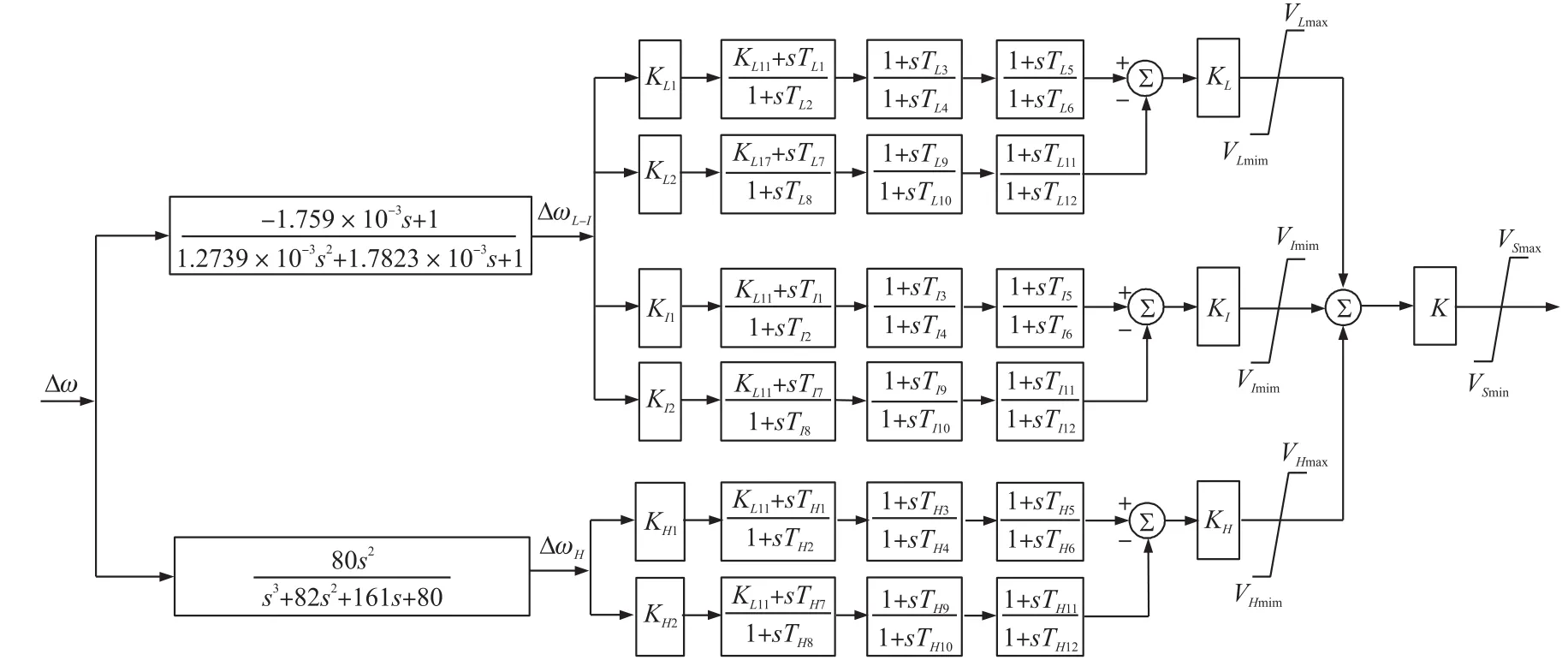
圖3PSS4B數學模型

PSS4B各頻段中心濾波器參數設置滿足在中心頻率處增益最大且相位為零，計算公式如下：

式中，FL是中心頻率，R是比例常數，IEEE推薦取1.2，此時KL1=KL2=66。

通過以上整定，在中心補償頻率處的放大倍數是1，而整個分支的放大倍數為頻段增益KL。各段中心濾波器和頻段增益確定后，可以得到一個簡單的PSS4B參數設置，但是各頻段互相疊加，不能完全解耦，需要考慮其相互影響。

每個頻段兩級超前滯后環節參數設置將在上述中心濾波環節以及頻段增益確定的基礎上影響PSS4B最終的頻率特性，設置上下分支完全相同，則可將其從兩分支中提取出來，如圖4所示。因此，需要整定的PSS4B參數歸納為：

低頻段：FL、KL、TL1、TL2、TL3、TL4

中頻段：FI、KI、TI1、TI2、TI3、TI4

高頻段：FH、KH、TH1、TH2、TH3、TH4

總增益：K

圖4PSS4B模型變型

對于PSS4B的參數優化仍然基于相位補償法，采用改進粒子群算法進行優化。通過對PSS4B模型以及參數分析，得知對比傳統PSS2A/B，PSS4B的3個頻段多出了3個中心濾波環節，且中心頻率范圍相隔較近，通過各頻段增益環節輸出后對其他頻段相頻特性影響最大。為了提高優化效率，減小各頻段之間的耦合影響，考慮將參數劃分為兩個部分，通過兩次相位補償對參數進行優化。首先按照一定的補償目標優化對頻段頻率特性影響最大的中心濾波環節以及頻段增益，然后在第1次相位補償的基礎上按照最終有補償頻率特性目標范圍優化超前/滯后環節時間常數。參數劃分如圖5所示（以低頻段為例），虛線框中部分為首次優化的參數，其他部分為二次優化的參數。

2.2基于粒子群的PSS參數優化［10］

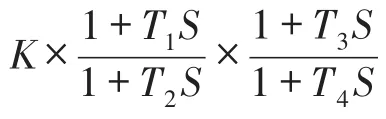
優化目標函數可以描述為式（8）：

其中ξi是影響小水電群送出的主導低頻振蕩模式的阻尼比，ξk是其它主導低頻振蕩模式的阻尼比，ξi0和 ξk0是阻尼比原始值；Ki，T1i和T3i是第i臺機組的待優化參數。

（1）參與PSS優化機組的篩選

根據機組參與主導振蕩模式的程度進行排序，選擇其中影響大的機組進行PSS參數優化。

一般的方法是利用參與因子進行機組的篩選。參與因子可以表示為 pki=φki×ψik，表示模式i中第k個狀態變量的相對參與程度。PSS在抑制低頻振蕩時，主要關注的狀態變量是發電機轉子角頻率ω。可以選擇ω對主導振蕩模式有較大參與因子的機組參與PSS優化。

由于機組PSS裝置的輸入是機組的ω和PG，輸出量Vpss疊加在機組的勵磁系統輸入端，從模式的可控性和可觀性角度，利用機組ω對模式的可觀性以及PSS輸出對模式的可控性的留數指標，分析機組對主導振蕩模式的參與程度，可以取得更好的效果。

（2）改進的尋優策略

優化目標要求機組PSS參數優化結果要滿足主導振蕩模式阻尼比大于等于其原始值的約束條件。而在粒子群尋優過程中，由于一些機組可能參與多個主導振蕩模式，因此其PSS參數可能會使一些主導振蕩模式阻尼比增大，而導致另一些主導振蕩模式阻尼比小于其原始值的情況，從而導致大量不可行解出現。

如果在尋優過程中僅利用可行解來尋找全局最優解，而不考慮不可行解在粒子群飛行中的引導作用，可能會降低搜索效率。而且在可行域占搜索空間比例很小或最優解位于邊界附近情況下，一些不可行解可能更接近全局最優解，包含更多有用信息，如果利用不可行解的信息來引導粒子群飛行，有利于尋找全局最優解。為此本文提出一種改進的搜索策略。

改進的策略為，粒子群找到的個體或全局極值，雖然不滿足約束條件，但只要在容許范圍內，即滿足g≤ε的條件，仍可以作為個體極值或全局極值的速度和位置更新。

該策略可以使尋優過程在迭代的初期，允許一些滿足容忍度閾值的不可行解提供信息給粒子群，隨著迭代進行，容忍度閾值不斷減小，對可行解的要求越來越高，有利于粒子群在可行解的指引下尋優。

2.3第一次相位補償

采用PSO算法進行第1次相位補償，種群中粒子表示為（FL，KL，FI，KI，FH，KH），補償目標為對無補償頻率特性實現適度預補償，并且為第2次相位補償留有一定裕度。目標函數為式（9）：

式中，φs為只包含首次優化參數的PSS4B的相頻特性，r為各頻段目標補償度，由各頻段無補償頻率特性決定。

約束條件為：

（1）當 0.04 Hz＜fi＜0.1 Hz時：r的取值范圍為［0°，10°］；

當0.1 Hz＜fi＜1 Hz時：r的取值范圍為［10°，15°］；

當1 Hz＜fi＜4 Hz時：r的取值范圍為［10°，20°］。

（2）FL的取值范圍為［0.01，0.1］；

FI的取值范圍為［0.1，1］；

FH的取值范圍為［1，10］；

KL，KI，KH的取值范圍為［1，10］。

2.4第二次相位補償

基于第1次相位補償，整定了3個頻段的中心頻率以及增益，第2次相位補償將優化整定3個頻段的超前-滯后環節參數。

仍然采用PSO算法，為了提高優化效率采用分頻段優化，即按照低頻段、中頻段、高頻段的順序，通過3次PSO尋優分別整定各頻段的超前-滯后環節時間常數T1，T2，T3，T4。

種群中每個微粒代表一組時間常數（T1，T2，T3，T4），優化的目標函數按照順序分別為：

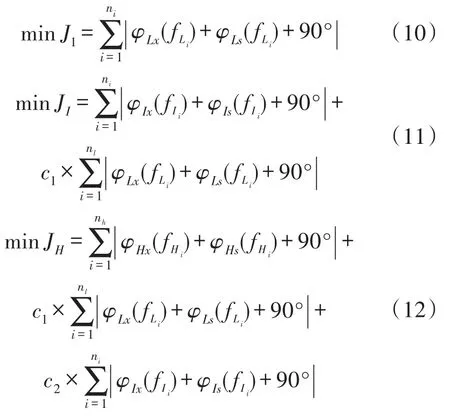
約束條件為：

式中，將無補償頻率特性按照3個頻段劃分為φLx，φIx，φHx，φLs，φIs，φHs為依次加入 3個頻段超前-滯后環節后PSS4B對應頻段的相頻特性，φL0，φI0，φH0為 3個頻段對應的有補償頻率特性，c1，c2為某頻段的補償環節對前面頻段頻率特性的影響因子。

2.5總增益K整定

相位補償法是從頻率特性上來優化整定PSS4B相關參數，最后總增益的整定為在該基礎上確定PSS4B附加阻尼轉矩的阻尼系數，并不影響PSS4B的相頻特性。目前通用的方法即為臨界增益法。臨界增益試驗的方法如下：在選定的相位補償參數下，緩慢增大PSS的增益，同時仔細觀察勵磁系統各可觀測量的變化，直到觀察到不穩定現象為止，將放大倍數確定為臨界增益的1/3～1/2，即認為是最佳增益［9］。

3　算例分析

為了對優化結果有效性進一步檢驗，圖5選取PSS2B典型參數、PSS2B優化參數、PSS4B典型參數、PSS4B優化參數和進行幅相頻特性對比，對比其波特圖可以明顯看到，不同的PSS在0.1 Hz～5.0 Hz有非常相似的相頻響應的波形，然而PSS4B優化的增益在關鍵的區間模型0.1 Hz～1.0 Hz頻率上表現更好，魯棒性強。

圖5　PSS2B和PSS4B幅頻相頻波特圖對比

對ABB公司的UNITROL 6800的勵磁調節器的典型PSS4B和優化PSS4B模型利用RTDS進行了仿真測試，被試機組有功功率300 MW，無功功率20 Mvar，分別在1.2 Hz、1.0 Hz、0.8 Hz、0.6 Hz、0.4 Hz、0.2 Hz和0.1 Hz的擾動，進行3%的定子電壓擾動，在典型PSS4B和優化PSS4B模型的試驗錄波數據如表1、表2所示，試驗波形如圖6、圖7所示。

表1　典型PSS4B模型測試數據

表2　優化PSS4B模型測試數據

圖6　典型PSS4B模型在不同頻率擾動下性能檢測及抑制效果

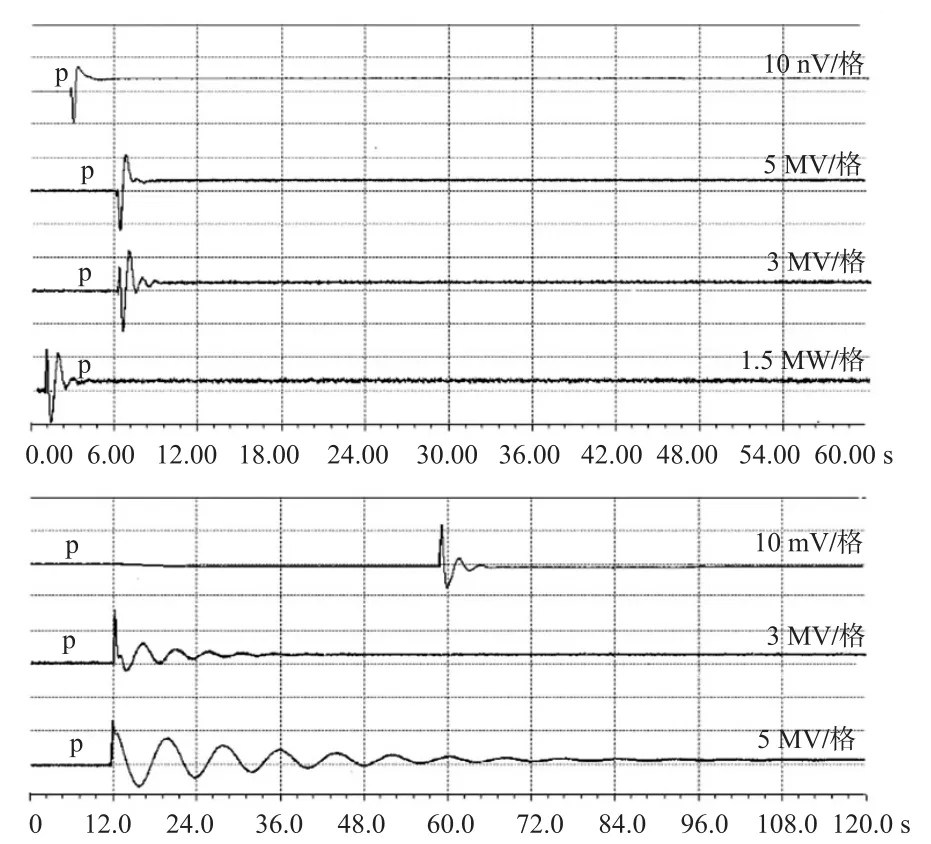
圖7　PSS4B優化模型在不同頻率擾動下性能檢測及抑制效果

有仿真試驗錄波結果來看，PSS4B對于有功振蕩的抑制效果，無論在高、中、低頻振蕩模式下均能提供最佳的阻尼效果，隨著頻率降低，PSS4B較PSS2B對各振蕩模式阻尼效果改善更明顯。進一步對上述系統進行試驗研究，對無PSS、PSS2A參數、PSS2B參數、PSS4B優化參數進行時域和頻域特性對比，如圖8和圖9所示。

圖8　無PSS、PSS2A和PSS4B優化模型對比

圖9　無PSS、PSS2B和PSS4B優化模型對比

通過無PSS系統、PSS2A、PSS2B和PSS4B參數優化對比，試驗結果表明，PSS2A和PSS2B模型對寬頻段范圍內調整相位不能很好的適應，PSS4B可以在更大的頻率范圍內提供更好的靈活性來獲得更好的調節性能。采用PSS4B參數優化方法的可以提升系統反應速度，縮小時間，給系統提供更大的阻尼效果。

4　結論

本文采用相位補償法和粒子群優化算法對PSS4B參數進行協調優化，實現了PSS4B在整個工作頻段上良好的補償效果，解決了目前PSS4B參數整定困難的問題，具有一定工程意義。優化后的PSS4B模型對于有功振蕩的抑制效果，無論在高、中、低頻振蕩模式下均能提供最佳的阻尼效果，隨著頻率降低，PSS4B較PSS2B對各振蕩模式阻尼效果改善更明顯。

經過長期的發展，發電機勵磁控制已經成熟，從勵磁的發展方向看，在控制技術方面有采用非線性及人工智能的、在元器件方面有采用全控型電力電子元件的，但有一個問題受到了忽視，就是勵磁系統自身故障的保護問題，目前仍然由分立的機組保護解決，對于此問題，勵磁技術科研人員應承擔更重要責任與義務。

［1］倪以信，陳壽孫.動態電力系統的理論與分析［M］.北京：清華大學出版社，2002：1-10.

［2］尚超，丁堅勇，馬曦.新型電力系統穩定器PSS4B的分析與仿真［J］.華東電力，2013（3）：575-578.

［3］湯偉.基于MATLAB的PSS的參數計算與仿真［D］.哈爾濱：哈爾濱理工人學，2010.

［4］華國輝，赫衛國，趙大偉，等.電力系統穩定器PSS4B模型的研究與實現［C］//2010年中力系統自動化學術會交集.

［5］管秀鵬，程林，孫元章.基于Prony方法的大型互聯電網PSS參數優化設計［J］.電力系統自動化，2006，30（25）：7-11.

［6］Kamwa I，Grondin R，Trudel G.IEEE PSS2B Versus PSS4B：The Limits of Performance of Modern Power System Stabilizers.Power Systems，IEEE Transactions on［J］.2005，20（2）：903-915.

［7］Grondin R，Kamwa I，Trudel G.Modeling and Closed-Loop Validation of a New PSS Concept，the Multi-Band PSS［C］//Power Engineering Society General Meeting，2003，IEEE，2003：1803-1809.

［8］Hua Guanghui，He Weiguo，Zhao Dawei.Research and Implementation on Power System Stabilizer PSS4B Model［C］//Electricity Distribution（CICED），2010 China International Conference on，2010：1-4.

［9］朱良合，李文意，毛承雄，等.新型電力系統穩定器模型分析及參數協調優化［J］.水電能源科學，2014，32（6）：171-175.

［10］劉蔚，趙勇，吳琛，等.一種提高多小水電群送出能力的PSS參數協調優化方法［J］.電力系統保護與控制，2015，43（4）：44-50.

［11］牛振勇，杜正春，方萬良.基于進化策略的多機系統PSS參數優化［J］.中國電機工程學報，2004，24（2）：22-27.

［12］石輝，張勇軍，徐濤.我國智能電網背景下的低頻振蕩應對研究綜述［J］.電力系統保護與控制，2010，38（24）：242-247.

［13］馬燕峰，趙書強.基于在線辨識和區域極點配置法的電力系統低頻振蕩協調阻尼控制［J］.電工技術學報，2012，27（9）：117-123.

［14］夏潮.并行電力系統穩定器的研究［D］.中國電力科學研究院，2007.

［15］邱磊，王克文，李奎奎，等.多頻段PSS結構設計和參數協調［J］.電力系統保護與控制，2011（5）：102-107.

［16］夏潮，劉增煌，朱方，等.兩分支分段補償的并行電力系統穩定器［J］.中國電機工程學報，2010（19）：20-25.

［17］王克文，李衍，倪相生.相位補償法設計雙頻段PSS［J］.電力系統及其自動化學報，2009（1）：1-7.

［18］杜文娟，王海風，曹軍.PSS就地相位補償法的模型和理論［J］.中國電機工程學報，2012（19）：36-41.

［19］楊立環，徐峰，胡華榮，等.電力系統穩定器PSS2A現場試驗及參數整定［J］.電力系統保護與控制，2010（1）：112-114.

［20］祁萬春，房鑫炎.基于混合粒子群優化算法的PSS參數優化［J］.繼電器，2005（13）：21-24.

［21］崔志華.微粒群優化算法［M］.科學出版社，2011.

［22］劉洲洲，李艷平.基于量子粒子群優化算法的壓縮感知數據重構方法［J］.傳感技術學報，2015，28（6）：836-841.

［23］吳雅靜，馬珺.基于提升小波與粒子群相結合的混沌信號降噪［J］.電子器件，2014，37（6）：1093-1097.

［24］王超，李森.變參數QPSO算法優化神經網絡的短期電力負荷預測［J］.電子器件，2014，37（4）：782-786.

［25］劉東，田雨波.基于改進粒子群算法的EBG結構優化設計？［J］.電子器件，2015，38（2）：38.

［26］沈鑫，王昕，趙艷峰，等.基于單周控制的并網逆變器在云南電網中的研究應用［J］.電子器件，2013，36（5）：722-727.

［27］沈鑫，曹敏，王昕，等.智能變電站的時鐘同步準確性及穩定性研究［J］.電子器件，2015，38（3）：655-660.

［28］王昕，劉清蟬，沈鑫，等.基于電容電流的高準確度CVT諧波測試系統研制及運用［J］.電子器件，2014，37（6）：1221-1227.

沈鑫（1981-），男，云南人，云南電網有限責任公司電力科學研究院，博士研究生，高級工程師，昆明市第十三批學術和技術帶頭人，主要研究方向為電能計量和智能電網技術，23755803@qq.com；

馬紅升（1978-），男，云南人，云南電網公司有限責任公司，碩士，高級工程師，主要研究方向為電力系統穩定分析與控制技術。

A Method of PSS4B Parameters Optimization Based on the Phase Compensation Method and Particle Swarm Algorithm*

SHEN Xin*，MAHongsheng，LI Shilin，WANG Xin，LIU Qingchan
（Yunnan Electric Power Research Institute；Kunming 650217，China）

With the development of power grid scale，power system low frequency oscillation is becoming an increasingly outstanding problem.Power system stabilizer is one of the effective measures which can solve the low frequency oscillation.Aiming at some problems existing in using of PSS，optimum research on the model parameters of power system stabilizer，based on the phase compensation method and particle swarm optimization algorithm.The RTDS is used to establish the simulation experiment，after optimized the model parameters of the wild band power system stabilizer.The results show that optimized PSS4B can meet the requirements of multiple frequency bands，and effectively suppress lowfrequency oscillation.

power system stabilizer（PSS）；phase compensation method；particle swarm optimization（PSO）；multiband；parameter optimization

TM712；TM44

A

1005-9490（2016）05-1244-07

項目來源：云南省教育廳重大專項研究項目（2015Z014）

2015-08-31修改日期：2015-10-17

EEACC:811010.3969/j.issn.1005-9490.2016.05.043