微型壓電振動發電機諧振頻率調節技術的研究*

閆　震，何　青，王東平，劉俊峰

（1.河北農業大學機電工程學院，河北保定071001；2.華北電力大學能源動力與機械工程學院，北京102206；3.河北農業大學現代科技學院，河北保定071001）

微型壓電振動發電機諧振頻率調節技術的研究*

閆震1*，何青2，王東平3，劉俊峰1

（1.河北農業大學機電工程學院，河北保定071001；2.華北電力大學能源動力與機械工程學院，北京102206；3.河北農業大學現代科技學院，河北保定071001）

具有高能量密度的微型壓電振動發電機可以無限、持續地為無線傳感器網絡提供能量。為了適應環境振源頻率的變化，提高壓電振動發電機的能量轉換效率，采用理論建模和數值分析的方法，研究了旁路電容調節振動發電機固有頻率的關鍵技術。建立壓電電容與壓電層楊氏模量的力學模型，分析壓電電容對壓電發電機固有頻率的影響規律，提出了單晶片和雙晶片壓電梁的電容頻率調節配置方案；分別研究厚度比、長度和寬度對開路、閉路剛度比及固有頻率比的影響特性，對結構參數進行了優化配置。

無線傳感器網絡；壓電式振動發電機；旁路電容；固有頻率

應用微機電加工技術制造的懸臂梁壓電式振動發電機可以無限、持續地為各種低功耗電子器件提供能量，有效地解決了無線傳感器網絡在苛刻工作環境中能源供給難題［1-9］。然而，懸臂梁壓電振動發電機對環境振源頻率的變化很敏感，若環境頻率偏離壓電發電機固有頻率2 Hz～3 Hz，將導致輸出功率急劇下降。為了提高懸臂梁壓電振動發電機的環境適應能力，通常采用附加外部機械裝置來改變懸臂梁的結構或剛度，以調節其固有頻率。但是，該方法增大了壓電發電機體積和制作難度，也提高了生產成本。針對上述問題，本文采用旁路電容調節壓電梁的固有頻率，以適應振源環境的變化，通過分析壓電梁的結構參數對旁路電容頻率調節范圍的影響規律，提出了結構參數優化配置方案，為提高有限體積懸臂梁壓電式振動發電機的發電能力，奠定了研究基礎。

1　旁路電容頻率調節理論建模

懸臂梁壓電發電機固有頻率公式

懸臂梁壓電發電機的固有頻率［10］為

式中，MS和MP分別為基板和壓電層的質量矩陣，KS和KP分別為基板和壓電層的剛度矩陣，C′是壓電電容矩陣，θ′是壓電機電耦合矩陣，KP+θ′TC′-1θ′為壓電層的等效剛度。壓電梁總等效剛度由基板機械剛度KS、壓電層機械剛度KP和機電耦合剛度θ′TC′-1θ′構成，其等效連接方式如圖1所示。

圖1　懸臂梁壓電發電機等效剛度

由式（6）可知，通過改變壓電層的機電耦合項或電容值，可以改變系統剛度，進而實現固有頻率的調節。但是，機電耦合項由壓電層材料特性和復合梁的幾何形狀決定，一般不易改變，因而只能通過改變壓電電容值來調節固有頻率。據此，設計在壓電層并聯旁路電容，通過調節系統的壓電電容值改變固有頻率。其原理為：系統總電容為旁路電容與壓電電容之和；當旁路電容短路CS=∞時，機電耦合剛度項θ′T（C′+CS）-1θ′=0，壓電梁等效剛度最小，固有頻率最低；隨著旁路電容值逐漸降低，機電耦合剛度項θ′T（C′+CS）-1θ′隨之升高，當降低到旁路電容開路狀態CS=0時，機電耦合剛度項達到最大值，等效剛度和固有頻率值最高，如圖2所示。

圖2　旁路電容頻率調節方式

由上述分析可知，旁路電容短路和開路狀態分別為固有頻率調節范圍的下極限和上極限狀態；壓電調節層的開路固有頻率與短路固有頻率之比，決定了壓電梁的諧振頻率調節范圍。

為了分析不同壓電梁結構對電容頻率調節范圍的影響，將雙晶片壓電梁的兩個壓電層分為能量收集層hp和頻率調節層ht，各壓電層具有獨立的收集和調節作用，通過改變各層的位置和厚度，分析其對剛度及固有頻率的影響，如圖3所示。為便于表述，將圖3（a）、圖3（b）和圖3（c）中的雙晶片壓電梁結構分別稱為雙晶片壓電梁A、雙晶片壓電梁B和雙晶片壓電梁C。

圖3　收集層、調節層和基板具有不同相對位置的雙晶片壓電梁結構圖

由于壓電和基板材料具有不同的彈性模量和密度，因此，在計算慣性矩前，必須對橫截面寬度進行轉換，將兩層材料以同一彈性模量表示，以確定復合梁橫截面中性軸的位置。據此，令基板作為轉換后的單一材料，定義彈性模量比［11］

由于基板材料的彈性模量大于壓電陶瓷的彈性模量，由式（7）可知，np和nt均小于1，因此，轉換后基板寬度b大于壓電層寬度npb和ntb。

在圖3（a）中，壓電梁的中性軸位置為

式中，復合梁各層的中性軸高度yˉi以梁的底部為基線。

慣性矩為

在圖3（b）中，梁的中性軸位置

慣性矩為

在圖3（c）中，梁的中性軸位置

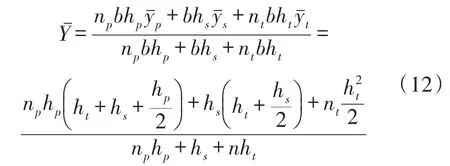
慣性矩為

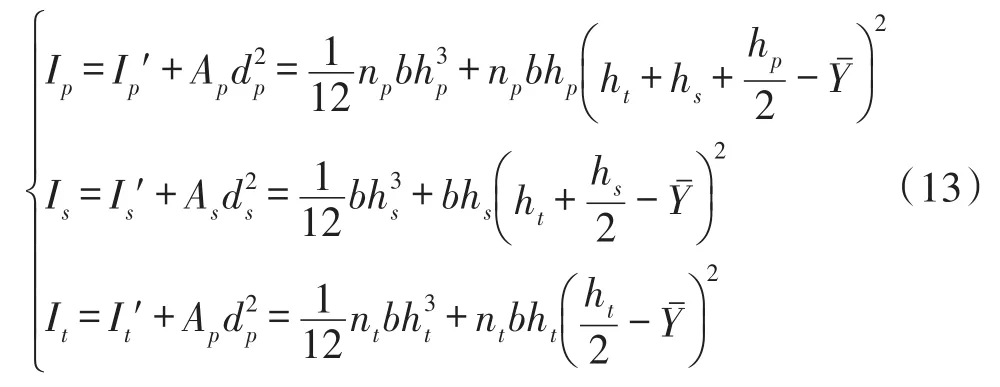
式中，As為基板的橫截面面積，Ap為壓電層的橫截面面積，ds為基板中性軸與復合材料中性軸的距離，dp為壓電層中性軸與復合材料中性軸的距離。

圖3中雙晶片壓電梁的彎曲剛度為

壓電調節層的彈性模量為［12］

式中，Cz為壓電電容Ct與并聯電容Cs之和。

當調節層為短路狀態時，旁路電容Cs=∞，因此Cz=∞，壓電調節層的彈性模量與柔順系數成反比

當壓電調節層為開路狀態時，則旁路電容Cs值為0，調節層的彈性模量為

由于壓電電容

因此，式（17）可寫為

由式（16）和式（18）可知，懸臂梁壓電發電機開路時的楊氏模量要大于短路時的楊氏模量。

上述分析表明，通過改變壓電調節層的旁路電容，能夠有效改變懸臂梁壓電發電機的彈性模量，從而使有效剛度發生變化，實現對固有頻率的調節。

2　旁路電容頻率調節數值分析

以表1中的單晶片壓電梁參數作為計算數據，雙晶片壓電梁參數與單晶片壓電梁相同，僅壓電層厚度為單晶片壓電梁壓電層厚度的1/2，研究旁路電容對固有頻率的影響規律，分析尺寸及材料參數與旁路電容頻率調節范圍的關系。由于旁路電容頻率調節方式通過改變壓電梁剛度來調節固有頻率，且開路和閉路固有頻率比決定頻率調節范圍，因此，本節通過式（18）、式（16）、式（14）和式（1）計算開路、短路剛度和固有頻率，分別研究厚度比、長度、寬度和材料參數對開路、短路剛度比及固有頻率比的影響規律，以壓電梁的固有頻率調節范圍和能量收集最大化為目標，優化結構尺寸和材料參數。

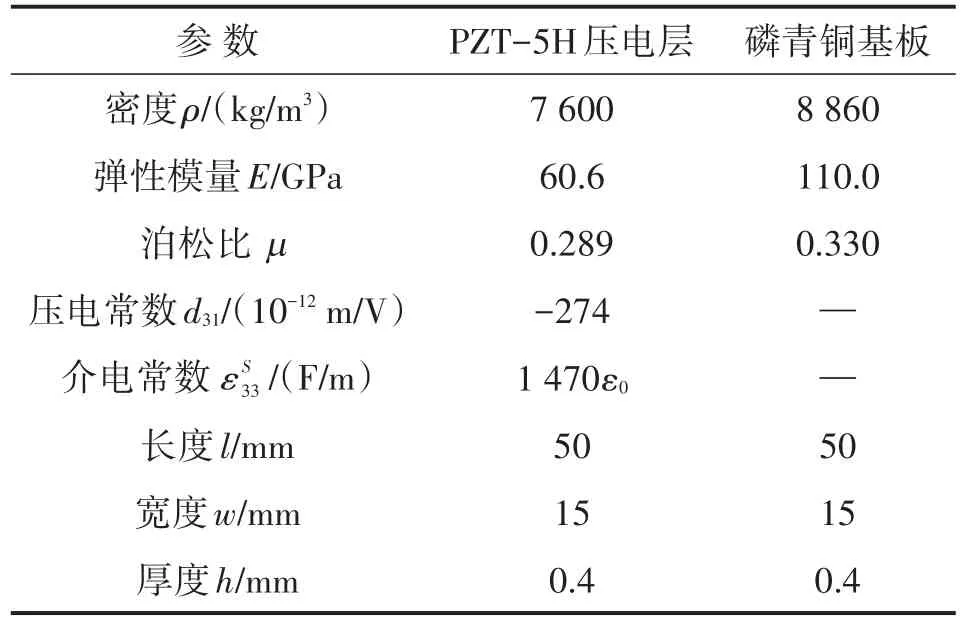
表1　單晶片壓電梁結構和材料參數

2.1旁路電容頻率調節特征

為了研究旁路電容對頻率調節范圍的影響規律，分析壓電梁固有頻率與短路固有頻率比隨旁路電容與壓電電容比的變化規律。結果表明，隨著旁路電容值的增加，壓電梁的固有頻率逐漸降低；連續調節旁路電容，可以得到開路頻率和閉路頻率間的任意頻率。同時還發現，單晶片和雙晶片壓電梁的旁路電容頻率調節規律基本一致，僅范圍不同，當0＜Cs/Cp＜5時，固有頻率變化較為明顯；當Cs/Cp＞10時，改變旁路電容值，壓電梁的固有頻率基本不會變化；雙晶片壓電梁C兩壓電層同時調節時，頻率調節范圍最大，而雙晶片壓電梁B頻率調節范圍較窄，如圖4所示。

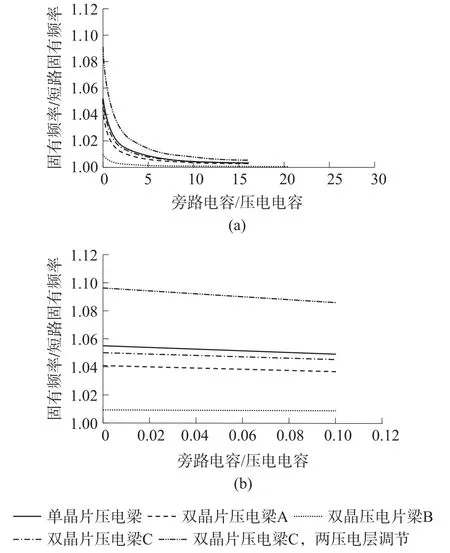
圖4　固有頻率比與電容比的關系

2.2厚度比對旁路電容頻率調節范圍的影響

壓電層厚度固定不動，僅改變基板厚度，研究單晶片壓電梁的開路、短路剛度比和固有頻率比隨基板厚度與壓電層厚度比的變化規律。研究結果如圖5所示。

圖5　單晶片壓電梁的剛度比和固有頻率比隨厚度比變化規律

從圖5中可以看出，剛度和固有頻率變化規律一致，僅范圍不同；在相同厚度比下，剛度的調節范圍要大于固有頻率的調節范圍；當厚度比位于0～2時，頻率調節范圍較寬，但是，當厚度比小于1時，壓電梁的中性軸不在基板內而位于壓電層，壓電片不能完全拉伸或壓縮，無法輸出最大能量，這時模擬的剛度已脫離真實狀態。據此，要使單晶片壓電梁穩定工作和具有較大頻率調節范圍，應選擇厚度比為1或略大于1。

固定壓電調節層厚度，改變基板與壓電收集層的厚度，分析雙晶片壓電梁A的厚度比對剛度和固有頻率調節范圍的影響，分析結果如圖6所示。

圖6　雙晶片壓電梁A的剛度比和固有頻率比隨厚度比的變化規律

在圖6（a）中，x軸為基板厚度與壓電調節層厚度比，y軸為壓電收集層厚度與壓電調節層厚度比，z軸為開路剛度與短路剛度比；在圖6（b）中，z軸為開路固有頻率與短路固有頻率比。從圖6中看出，與單晶片壓電梁類似，當厚度比越小時，剛度比越大，雙晶片壓電梁A固有頻率可調范圍也越寬。這是由于厚度比較小時，壓電調節層相對較厚，剛度和固有頻率可調范圍相對較大；當兩厚度比相同時，由于梁的中性軸位于壓電調節層內，振動時剛度調節特性受到影響，剛度比急劇下降。

固定壓電調節層厚度，改變基板與壓電收集層的厚度，分析雙晶片壓電梁B厚度比對剛度和固有頻率調節范圍的影響，分析結果如圖7所示。從圖7中可以看出，厚度比越小，剛度和固有頻率可調范圍越大；在兩個厚度比中，任一厚度比大于2時，其剛度和固有頻率調節范圍將顯著下降。

圖7　雙晶片壓電梁B的剛度比和固有頻率比隨厚度比的變化規律

固定壓電調節層厚度，改變基板與壓電收集層的厚度，分析雙晶片壓電梁C的厚度比對剛度和固有頻率調節范圍的影響，分析結果如圖8所示。對比圖7可以發現，由于雙晶片壓電梁B和雙晶片壓電梁C兩種結構的壓電調節層所處的相對位置一致，因此兩者的厚度比對剛度比及固有頻率比的影響規律相似，僅調節范圍值略有差異。

當雙晶片壓電梁C的兩壓電層均為調節層時，分析厚度比對剛度和固有頻率調節范圍的影響，分析結果如圖9所示。從圖9中可以看出，當基板與調節層厚度比約為1、收集層和調節層厚度比在0.3～0.5之間時，固有頻率可調節范圍較寬；當基板與調節層厚度比小于0.5時，剛度和固有頻率調節范圍迅速減小；相對其它配置，該結構的固有頻率可調節范圍最大。

圖8　雙晶片壓電梁C的剛度比和固有頻率比隨厚度比的變化規律

圖9　兩壓電層調節的雙晶片壓電梁C的剛度比和固有頻率比隨厚度比的變化

通過以上分析可知，雙晶片壓電梁A和雙晶片壓電梁B的最大頻率調節范圍低于單晶片壓電梁，且加工成本高，振動性能不穩定。因此，為提高頻率調節范圍和降低加工成本，應優先選用單晶片壓電梁。另外，由于雙壓電層調節的雙晶片壓電梁C剛度比和固有頻率比的變化范圍較大，并且振動性能穩定，因此，也應作為重點選用對象。

2.3長度和寬度對旁路電容頻率調節范圍的影響

固定厚度比和材料參數，分別改變長度值和寬度值，分析長度、寬度對旁路電容頻率調節范圍的影響規律，分析結果如圖10和圖11所示。從圖10和圖11中可以看出，長度和寬度的變化對固有頻率的調節范圍沒有任何影響。

圖10　電容頻率調節范圍與長度的關系

圖11　寬度與電容頻率調節范圍的關系

3　結論

為了實現旁路電容對壓電式振動發電機固有頻率的有效調節，分析了壓電電容對振動發電機固有頻率影響的基本規律，研究了結構和材料參數對壓電梁固有頻率比的影響特性，得出如下結論：

（1）壓電調節層的開路固有頻率與短路固有頻率之比決定了懸臂梁壓電發電機固有頻率調節范圍；旁路電容與壓電電容比值小于5時，頻率調節效果明顯。

（2）單晶片壓電梁和雙晶片壓電梁C的固有頻率調節范圍要優于雙晶片壓電梁A和雙晶片壓電梁B。

［1］闞君武，王淑云，彭少鋒，等.多振子壓電發電機的輸出特性［J］.光學精密工程，2011，19（9）：2108-2116.

［2］張永良，林政.海洋波浪壓電發電裝置的進展［J］.水力發電學報，2011，30（5）：145-148，169.

［3］張磊，房立清，郭德卿，等.單晶壓電振子結構二維優化設計［J］.壓電與聲光，2013，35（6）：889-892.

［4］蔣樹農，郭少華，李顯方，等.單壓電片懸臂梁式壓電俘能器效能分析［J］.振動與沖擊，2012（19）：90-94.

［5］王兆強，劉海利，徐天柱，等.諧振式壓電疊堆的高效換能結構研究［J］.振動與沖擊，2011，30（12）：125-128.

［6］劉祥建，陳仁文.壓電振動能量收集裝置研究現狀及發展趨勢［J］.振動與沖擊，2012，31（16）：169-176.

［7］林偉，卿輝，陳文，等.基于新型電源供電的無線傳感網絡節點設計［J］.壓電與聲光，2011，33（3）：498-500，508.

［8］何青，閆震.壓電振動發電機理論建模與發電性能研究［J］.河北農業大學學報，2012，35（1）：106-110.

［9］閆震，何青.激勵環境下懸臂梁式壓電振動發電機性能分析［J］.中國電機工程學報，2011，31（30）：140-145.

［8］Ericka M，Vasic D，Costa F，et al.Energy Harvesting from Vibration Using a Piezoelectric Membrane［J］.Journal De Physique Iv，2005，128：187-193

［9］Wang S，Kwok H L，Sun C L，et al.Energy Harvesting with Piezoelectric Drum Transducer［J］.Applied Physics Letters，2007，90（11）：113506-113509.

［10］Nesbitt W Hagood，Walter H Chung，Andreas Von Flotow.Modelling of Piezoelectric Actuator Dynamics for Active Structural Control［J］.Journal of Intelligent Material Systems and Structures，1990，1（3）：327-354.

［11］單輝祖.材料力學Ⅱ［M］.北京：高等教育出版社，1999：15-19.

［12］William W Clark.Vibration Control with State-Switched Piezoelectric Materials［J］.Journal of Intelligent Material Systems and Structures，2000，11（4）：263-272.

閆震（1976-），男，河北保定人，講師，博士（后），主要從事無線傳感器網絡及微能源技術的研究工作，參與及主持國家863計劃，河北省自然科學基金等多項課題的研究，已發表相關學術論文20余篇，申請及獲批專利5項，qceftgh@126.com。

Study on Piezoelectric Vibration Generator Based on Shut Capacitor Frequency Regulation Technology*

YAN Zhen1*，HE Qing2，WANG Dongping3，LIU Junfeng1
（1.Mechanic&Electronic College，Agricultural University of Hebei，Baoding Hebei 071001，China；2.School of Energy Power and Mechanical Engineering，North China Electric Power University，Beijing 102206，China；3.Department of modern science&technology，Agricultural University of Hebei，Baoding Hebei 071001，China）

Piezoelectric vibration generator made in MEMS can infinite and continue to supply energy for low power electric device.For adapting change of vibration source frequency，theoretical modeling and numerical analysis are adopted，and key technology of shunt capacity regulating inherent frequency is studied to enhance energy conversion efficiency of vibration generator.Mechanical model between piezoelectric capacitance and Young modulus of piezoelectric layer is established to analyze influence rule of piezoelectric capacitance to inherent frequency of piezoelectric generator，and capacitance frequency adjustment allocation plan of unimorph and bimorph beam are put forward；influencing characteristic of thickness ratio，length，width and material parameter to open circuit，closed circuit stiffness ratio and inherent frequency ratio is studied respectively，and optimal configuration of structural and material parameter is conducted.

wireless sensor network；piezoelectric vibration generator；shut capacitor；inherent frequency

TH122

A

1005-9490（2016）05-1067-06

項目來源：河北省自然科學基金項目（E2013204069）；保定市科學研究與發展計劃項目（13ZG020；13ZF005）；河北農業大學理工基金項目（LG201401）

2014-12-25修改日期：2015-01-27

EEACC:834010.3969/j.issn.1005-9490.2016.05.010