7.1統計

陳為賢　康松

康松，山東省淄博市博山區教研室數學教研員，多次參加淄博市中考命題工作，中學高級教師，淄博市教學能手，山東省縣級教師培訓機構教學能手，三次獲山東省中小學教育科研優秀成果一等獎，省級以上刊物上發表論文500余篇，擔任山東文藝出版社《同步訓練》分冊副主編并承擔編寫工作。

重點難點易混易錯點剖析

復習重點：利用全面調查與抽樣調查（以抽樣調查為重點）收集和整理數據，明晰總體、個體、樣本、樣本容量等概念，利用統計圖表（以直方圖為重點）描述數據，收集、整理、描述和分析數據并得出結論，根據統計結果作出簡單的判斷和預測，利用平均數（主要是加權平均數）、中位數、眾數以及方差等統計量分析數據的集中趨勢和離散情況，用樣本的平均數和方差估計總體的平均數和方差，

復習難點：對統計知識的靈活運用，理解用樣本估計總體的統計基本思想，根據問題需要選擇適當的統計圖描述數據，準確利用直方圖描述數據，理解加權平均數“權”的意義，選擇適當的統計量表示數據的集中趨勢，方差的計算等，

常用度量集中趨勢的統計量有平均數、中位數、眾數等，平均數的計算要用到所有數據，能充分利用數據提供的信息，但受極端值的影響較大，中位數、眾數不受極端值的影響，方差是統計中常用的一種刻畫數據離散程度的統計量，方差越大，數據的波動越大，方差越小，數據的波動越小，

易混易錯點：

（1）全面調查與抽樣調查的調查方式選擇不當，在抽樣調查中對樣本的選取不當，或是對總體、個體、樣本、樣本容量等概念理解不準確，主要根據具體的調查對象、范圍來確定調查方式，區分全面調查和抽樣調查主要看調查的對象是部分還是全體，總體是一個確定的量，而樣本是一個變化的量，一個總體可以有多個樣本，還要注意樣本容量沒有單位，

（2）對統計圖表示的含義及具有的不同特點理解不準確，不能根據自己的需要和具體問題選擇適當的統計圖，對于統計圖的選擇，要清楚地表示出每個項目的具體數目就選擇條形統計圖，要清楚地反映事物的變化情況就選擇折線統計圖，要清楚地表示出各部分在總體中所占的百分比就選擇扇形統計圖，

（3）不能正確選擇平均數、眾數、中位數、方差等描述數據的特征，對于平均數、眾數、中位數的選用，要注意平均數的大小與一組數據中的每個數據都有關，中位數僅與數據的排列位置有關，眾數著眼于對各數據出現次數的考察，一組數據的平均數、中位數只有一個，但眾數可能不止一個，一組數據的眾數一定在原數據中，但平均數、中位數不一定在原數據中，求中位數時要注意排序，還要弄清楚數據的個數是奇數還是偶數。

點撥：本題考查條形統計圖、扇形統計圖與概率公式的綜合運用，理解各種統計圖的含義及其所反映數據的特點，從不同的統計圖中得到必要的信息是解決問題的關鍵，同時還要靈活運用數形結合等數學思想方法，本題的易錯點是不能準確獲取統計圖中的信息，

三全面調查與抽樣調查

例2（2015·通遼）下列調查適合抽樣調查的是（

），

A.審核書稿中的錯別字

B.對某社區的衛生死角進行調查

C.對八名同學的身高情況進行調查

D.對中學生目前的睡眠情況進行調查

解析：本題考查全面調查與抽樣調查的應用，正確區分全面調查與抽樣調查是解題關鍵，審核書稿中的錯別字必須準確，故須普查：對某社區的衛生死角進行調查，調查數量不是很大，應該普查；對八名同學的身高情況進行調查，人數不多容易調查，適合普查；對中學生目前的睡眠情況進行調查，中學生的人數比較多，適合采取抽樣調查，故選D，

點撥：一般來說，對于具有破壞性的調查、無法進行普查、普查的意義或價值不大時，應選擇抽樣調查；對于精確度要求高的調查，事關重大的調查往往選用普查，一般由普查得到的調查結果比較準確，但所費人力、物力和時間較多。而抽樣調查得到的調查結果比較近似，本題的易錯點是混淆全面調查與抽樣調查的適用范圍，

三統計量的選擇

例3

（2015·長沙）一家鞋店在一段時間內銷售了某種女鞋30雙。各種尺碼鞋的銷售量如表1所示，你認為商家更應該關注鞋子尺碼的（

），

解析：根據平均數、中位數、眾數、方差的意義分析判斷，即可得出鞋店老板最關心的數據，由于眾數是表明一組數據出現次數最多的統計量，據此可以確定進貨的數量，所以商家更應該關注的是眾數，故選C。

點撥：本題考查了統計的有關知識，主要是統計量的選擇，反映數據的集中趨勢的統計量有平均數、中位數、眾數等，反映數據的離散程度的統計量有方差等，各有其優勢與局限性，因此要對統計量進行合理的選擇和恰當的運用，

點撥：在關于穩定性的實際問題中，只有在平均數相同的情況下。比較方差的大小才有意義，此題主要考查了方差的性質和應用，要熟練掌握，解答此題的關鍵是要明確方差是反映一組數據波動大小的一個量，方差越大，則數據與平均值的離散程度越大，穩定性越差；反之，則它與其平均值的離散程度越小，穩定性越好，

點撥：此題考查了算術平均數和方差的定義，平均數是所有數據的和除以數據的個數，方差是一組數據中各數據與它們的平均數的差的平方的平均數，先根據平均數的定義確定出X的值，再根據方差的計算公式求出這組數據的方差，本題的易錯點是只計算各數據與它們的平均數的差的平方，忘記取平均數，

例6

（2015·昆明）2015年4月25日，尼泊爾發生了里氏8.1級地震，某中學組織了獻愛心捐款活動，該校數學興趣小組對本校學生獻愛心捐款額做了一次隨機抽樣調查，并繪制了不完整的頻數分布表（如表2）和頻數分布直方圖（如圖2所示，每組含前一個邊界值，不含后一個邊界值）。

點撥：本題考查了頻數分布表、頻數分布直方圖，也考查了用樣本估計總體及數形結合的數學思想方法，從頻數分布表、頻數分布直方圖獲取正確的信息是解題的關鍵，利用統計圖表獲取信息時，必須認真觀察、分析、研究，這樣才能作出正確的判斷并解決問題，本題的中考失分點是估計這次活動中愛心捐款額不低于20元的學生有多少人時，只考慮樣本而沒有用樣本估計總體。

中考命題預測

1.質檢部門為了檢測某品牌電器的質量，從同一批次共10000件產品中隨機抽取100件進行檢測，檢測出次品5件，由此估計這一批次產品中的次品件數是（

），

A.5

B.100

C.500

D.10000

2.下列說法正確的是（

），

A.為了檢測一批電池使用時間的長短。應該采用全面調查的方法

B.方差反映了一組數據的波動大小，方差越大。波動越大

C.打開電視正在播放新聞節目是必然事件

D.為了了解某縣初中學生的身體情況，從八年級學生中隨機抽取50名學生作為總體的一個樣本

3.九年級（3）班共有50名同學，如圖4是該班一次體育模擬測試成績的頻數分布直方圖（滿分為30分，成績均為整數），若將不低于23分的成績評為合格，則該班此次成績達到合格的同學占全班人數的百分比是

，

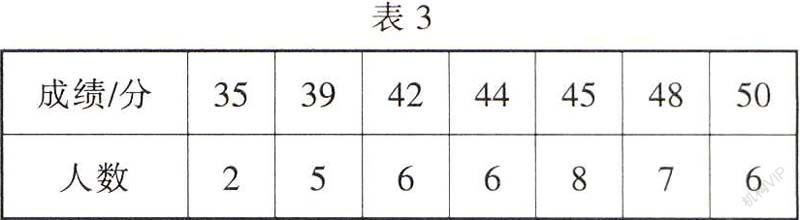
4.某校九年級（1）班全體學生2015年初中畢業體育考試的成績統計如表3，

根據表3中的信息判斷。下列結論中錯誤的是（

），

A.該班一共有40名同學

B.該班學生這次考試成績的眾數是45分

C.該班學生這次考試成績的中位數是45分

D.該班學生這次考試成績的平均數是45分

5.李華根據演講比賽中九位評委所給的分數制作了一個表格如表4，

如果要去掉一個最高分和一個最低分，則表中數據一定不發生變化的是（

），

A.平均數B.眾數C.方差D.中位數

6.某商場統計了去年1～5月A，B兩種品牌冰箱的銷售情況，并將獲得的數據繪制成折線統計圖，如圖5，

（1）分別求該商場這段時間內A，B兩種品牌冰箱月銷售量的中位數和方差。

（2）根據計算結果，比較該商場1-5月這兩種品牌冰箱月銷售量的穩定性。