高職院校數(shù)學建模競賽的研究與實踐

陳利群

全國大學生數(shù)學建模競賽創(chuàng)辦于1992年，每年一屆，目前已成為全國高校規(guī)模最大的基礎性學科競賽，也是世界上規(guī)模最大的數(shù)學建模競賽。2015年，來自全國33個省/市/自治區(qū)（包括香港和澳門特區(qū)）及新加坡和美國的1326所院校、28665個隊（其中本科組25646隊、專科組3019隊）、近86000名大學生報名參加本項競賽，參賽學校的數(shù)量和學生的數(shù)量以年均18%的速度增長。從統(tǒng)計數(shù)據(jù)可以看出，大學生數(shù)學建模競賽不但得到了本科高校的肯定，而且受到了高職院校的認同。隨著此項競賽的蓬勃發(fā)展，數(shù)學建模工作者應該保持清醒的頭腦，不能為了參賽而參賽，有必要深入分析一下高職院校的數(shù)學建模的深層思想和方法在深化教學改革、促進課程建設等方面的作用。

一、高職數(shù)學建模題目的現(xiàn)實背景

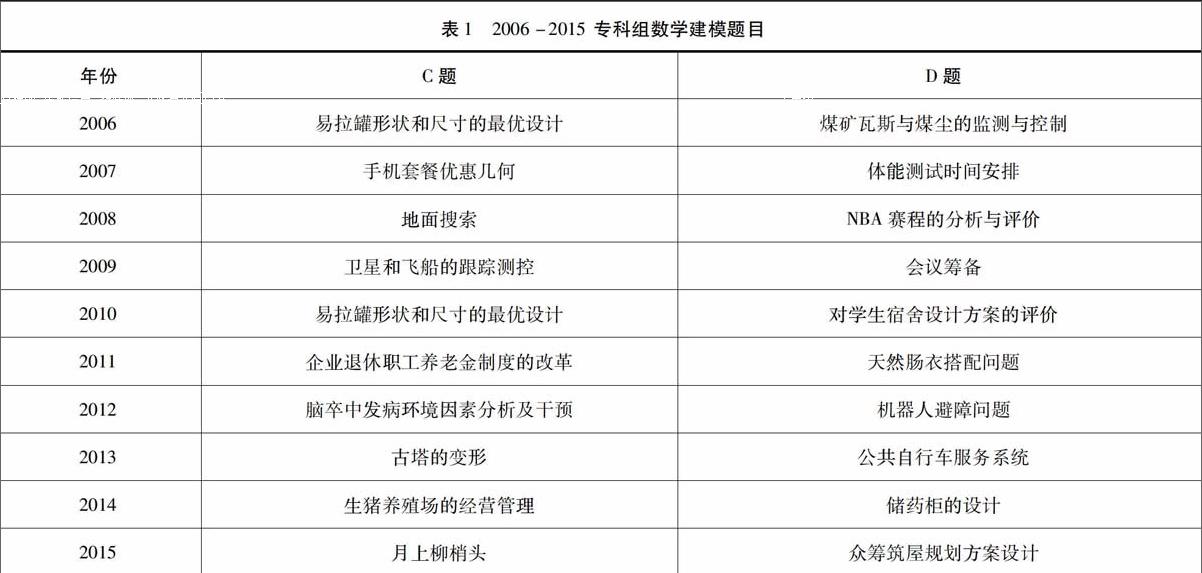
數(shù)學建模是一種數(shù)學的思考方法，是運用數(shù)學的語言和方法，通過抽象、簡化建立能近似刻畫并“解決”實際問題的一種強有力的數(shù)學手段。數(shù)學建模競賽的宗旨是培養(yǎng)大學生用數(shù)學方法解決實際問題的意識和能力，整個賽事是完成一篇包括問題的闡述分析，模型的假設和建立，計算結(jié)果及討論的論文。數(shù)學模型競賽與通常的數(shù)學競賽最大的不同就是它來自實際問題或有明確的實際背景。專科數(shù)學建模題目的實際意義比本科題目的實際意義更強，涉及面寬，有社會、經(jīng)濟、管理、生活、環(huán)境、自然現(xiàn)象、工程技術以及現(xiàn)代科學中出現(xiàn)的新問題等。這一點可從近10年的專科組數(shù)學建模題目看出，如表1所示。

二、高職數(shù)學建模題目的解題方法

從歷年數(shù)學建模競賽題目來看，解題方法主要包括以下三大類。

1.機理分析法——從基本物理定律以及系統(tǒng)的結(jié)構(gòu)數(shù)據(jù)來推導出模型

（1）比例分析法：建立變量之間函數(shù)關系的最基本最常用的方法。

（2）代數(shù)方法：求解離散問題（離散的數(shù)據(jù)、符號、圖形）的主要方法。

（3）邏輯方法：是數(shù)學理論研究的重要方法，對社會學和經(jīng)濟學等領域的實際問題，在決策、對策等學科中得到廣泛應用。

（4） 常微分方程：解決兩個變量之間的變化規(guī)律，關鍵是建立“瞬時變化率”的表達式。

（5）偏微分方程：解決因變量與兩個以上自變量之間的變化規(guī)律。

2.數(shù)據(jù)分析法——從大量的觀測數(shù)據(jù)利用統(tǒng)計方法建立數(shù)學模型

（1） 回歸分析法：用于對函數(shù)f（x）的一組觀測值（xi，f（xi））（i=1，…，n），確定函數(shù)的表達式，由于處理的是靜態(tài)的獨立數(shù)據(jù)，故稱為數(shù)理統(tǒng)計方法。

（2）時序分析法：處理的是動態(tài)的相關數(shù)據(jù)，又稱為過程統(tǒng)計方法。

3.仿真和其他方法

（1）計算機仿真（模擬）：實質(zhì)上是統(tǒng)計估計方法，等效于抽樣試驗：

① 離散系統(tǒng)仿真：有一組狀態(tài)變量。

② 連續(xù)系統(tǒng)仿真：有解析表達式或系統(tǒng)結(jié)構(gòu)圖。

（2）因子試驗法：在系統(tǒng)上作局部試驗，再根據(jù)試驗結(jié)果進行不斷分析修改，求得所需的模型結(jié)構(gòu)。

（3）人工現(xiàn)實法：基于對系統(tǒng)過去行為的了解和對未來希望達到的目標，并考慮到系統(tǒng)有關因素的可能變化，人為地組成一個系統(tǒng)。

三、高職院校參加全國大學生數(shù)學建模競賽的思考

盡管高職院校參加全國大學生數(shù)學建模競賽的熱情依然高漲，但是作為數(shù)學建模競賽指導教師必須保持清醒的頭腦，不能盲目為了競賽而競賽，必須擺正數(shù)學建模競賽的地位，明確參加數(shù)學建模競賽的目的，樹立正確的數(shù)學建模教育觀念。數(shù)學建模教育應該是一個有機的整體，學生、教師、學校和社會應該有機的聯(lián)動起來。

1.與學生的實踐活動有機結(jié)合

在數(shù)學建模競賽過程中收獲最大的是學生，凡是經(jīng)歷了競賽的學生都能夠真正體會到“一次參賽，終身受益”這句話。具體來說，競賽訓練了學生思考問題、解決問題的能力，培養(yǎng)了想象力、觀察力、學習能力、創(chuàng)新精神和團隊合作能力，等等。

但是很多學生參加過一次競賽后，就與數(shù)學建模完全隔絕開來，沒有得到繼續(xù)的鍛煉和持續(xù)的培養(yǎng)，這是非常可惜的。因此，數(shù)學建模指導教師應在賽后安排一些實踐性內(nèi)容，如數(shù)學建模實驗、社會實踐活動等，讓學生親自去建立模型，體會利用數(shù)學建模方法解決實際問題的意義。要是學生學有所用，鼓勵他們參加更高層次的數(shù)學建模競賽，在競賽中進一步提高自己的水平；與此同時，要鼓勵學生在校園科技活動、畢業(yè)實習、畢業(yè)設計、創(chuàng)新創(chuàng)業(yè)活動中使用所學到建模方法，提升自己的能力。

2.與教師的素質(zhì)培養(yǎng)相結(jié)合

數(shù)學建模教學是多門數(shù)學分支內(nèi)容的重組，數(shù)學建模活動是綜合性很強的學習和訓練，在一個問題中可能涉及到概率論與數(shù)理統(tǒng)計、微積分、運籌學等多門數(shù)學科目，還可能涉及工作、經(jīng)濟、醫(yī)療等領域，這就要求指導教師必須具備對這種交叉學科和交叉知識有效整合及快速學習的能力，同時還要熟練掌握第二部分提高的這些建模方法。數(shù)學建模指導教師在指導學生參加數(shù)學建模競賽的過程中，教師自身的知識結(jié)構(gòu)可以得到優(yōu)化，提升教學水平、業(yè)務能力和科研水平。同時，數(shù)學建模競賽也為教師提供了學術研究的方向。

3.與學校的課程建設相結(jié)合

高職院校數(shù)學以培養(yǎng)應用性人才為主，所以我們的高等數(shù)學課程應當強調(diào)應用性教學，在實踐應用中以必須和夠用為原則。高等數(shù)學的課程建設應注意自身特點，以培養(yǎng)學生的學習能力和分析解決問題的能力，而數(shù)學建模競賽正好能夠培養(yǎng)學生的以上所有能力。所以，在教學實踐中將數(shù)學建模思想與方法融入數(shù)學教學中去，在課堂教學中努力做到先引案例，再提出問題，探索出解決問題的數(shù)學建模方式，最大限度地把數(shù)學與專業(yè)以及實際生活結(jié)合起來，應該是高職院校數(shù)學教學改革新的發(fā)展方向。正如很多學者所提到的，“全國大學生數(shù)學建模競賽實際上是一項不打亂教學秩序的教學改革實驗”。

4.與社會的創(chuàng)新創(chuàng)業(yè)相結(jié)合

2015年5月8日國務院辦公室廳印發(fā)的《國務院辦公廳關于深化高等學校創(chuàng)新創(chuàng)業(yè)教育改革的實施意見》指出，自2015年起全面深化高校創(chuàng)新創(chuàng)業(yè)教育改革。一方面，數(shù)學建模競賽題目來源于實際，具有現(xiàn)實意義，如“公共自行車服務系統(tǒng)”“儲藥柜的設計”“生豬養(yǎng)殖場的經(jīng)營管理”；另一方面，參加數(shù)學建模競賽的過程極大地提高了學生的創(chuàng)新能力。所以對于高職院校而言，如果利用好了數(shù)學建模競賽這一工具，對整個學校的創(chuàng)新創(chuàng)業(yè)教育會起到很大的促進作用。

四、結(jié)束語

全國大學生數(shù)學建模競賽參賽規(guī)模龐大、創(chuàng)辦時間較長，不能與一般的競賽同日而語，其邊際效益和附加價值可能已經(jīng)遠遠超過了比賽本身。作為數(shù)學建模指導教師，理應站在一個更高的高度，盡自己所能最大限度地發(fā)揮數(shù)學建模競賽在學生實踐、教師培養(yǎng)、課程建設以及社會創(chuàng)新創(chuàng)業(yè)的作用。