基于RANS方法超空泡流數值計算方法研究

杜佩佩，肖昌潤，張 露，鄭文龍，焦玉超

(海軍工程大學 艦船工程系，武漢 430033)

?

【基礎理論與應用研究】

基于RANS方法超空泡流數值計算方法研究

杜佩佩，肖昌潤，張 露，鄭文龍，焦玉超

(海軍工程大學 艦船工程系，武漢 430033)

為了得到超空泡流準確的數值計算方法，基于烏克蘭國家科學院IHM的空泡形態計算經驗公式與Logvinovich空泡截面獨立擴張原理，利用數值優化的方法，建立了空泡形態計算模型；采用有限體積法驗證了超空泡流的數值離散方法，對不同空化數下，5種兩方程RANS模型進行了數值計算，數值計算結果與基于經驗公式的空泡驗證模型比較表明：Kω-Sst模型相比其他兩方程RANS模型準確度更高，關于空泡最大截面直徑的無量綱計算誤差小于14%；對空泡長度的數值計算誤差小于8%，空化數小于0.01時，小于4%。基于建立的準確數值計算模型，對空化數為0.015時超空泡航行體進行了流場特性數值計算。結果表明：由于空化器銳緣影響，在空化器后部形成了高速氣流區域并且存在明顯的速度梯度，艏部空化器附近承受靜水壓力達123個大氣壓。基于數值計算結果，為超空泡航行體設計提供了改進意見。

超空泡；湍流模型；有限體積法；CFD

超空泡技術早期主要通過理論研究，利用試驗進行理論修正，得到了很多經典的空泡流知識：如Helmholtz等人的自由流線理論， Levi-Civita[1]和Villat[2]在其基礎上進一步的研究，增強了該理論在強烈擾動和高彎曲度繞流問題的適用性；Wu[3]經過一系列分析，提出了一種非線性自由流線理論，可以解決非零空化數的空泡流問題，但是對復雜繞流問題的處理能力，尤其是其尾部封閉區域超空泡流的水動力問題，至今沒有得到很好解決。

對于超空泡航行體的CFD模擬，主要是基于RANS方法的兩方程渦黏模型和Reynolds代數應力模型(ASM)。涉及到兩相、甚至三相以上的多相流問題，自然超空泡的研究主要是應用均相流的Mixture模型，通氣超空泡的研究主要使用VOF模型[4]。對于空泡產生過程中水汽質量輸運過程，早期主要使用Singhal等人提出的Singhal完全空化模型進行分析，近年來主要應用基于Rayleigh-Plesset方程的Zwart-Gerber-Belamri模型和Schnerr and Sauer模型。

1969年，在Reichardt等人的研究基礎上，Logvinovich提出了可以解決非定常軸對稱空泡問題的Logvinovich原理(即空泡截面獨立膨脹原理)。Serebryakow[5]、Pellone[6]等人對該理論進行了完善，推導出幾個適用性更強的空泡截面發展方程，用偏微分方程加入空泡延遲效應研究空泡截面發展。隨后Serebryakow等[5]利用細長體理論，分析超空泡航行體跨、超音速運行時的定常流動，建立了一系列空泡發展模型。國內高強等[7]主要在該理論的基礎上推導了超空泡的形態發展方程和跨、超音速流動時的微積分方程，開始利用回轉體線性源匯的方法，求解超空泡航行體的空泡形態尺寸和流場壓力分布情況。

對于流場計算過程，主要通過湍流模型對計算方程進行封閉。文獻[8]比較了ASM模型、RNGk-ε模型和標準的k-ε模型結合3種壁面函數處理方法，認為ASM模型和RNGk-ε模型，同時結合增強壁面函數法計算精度較高；文獻[9]選用了RNGk-ε模型，認為其可以更好地處理應變率高、流線變化大的流動問題；文獻[10]比較了SSTk-ωDES、k-ε模型對航行體非定常運動過程的數值模擬，認為SSTk-ωDES模型精度更高。

由于超空泡流本身的復雜性，超空泡航行體CFD數值模擬方法難度較高。截止目前為止，多通過空泡形態以及數值模擬結果相互比較的方法驗證或者選取計算模型，還沒有給出定量的數值比較和較為準確的超空泡流場的CFD算法，本文應用基于Rayleigh-Plesset方程的Schnerr and Sauer空化模型，選用Mixture的均相流模型，基于烏克蘭國家科學院IHM的空泡形態計算經驗公式與Logvinovich空泡截面獨立擴張原理建立新的空泡形態計算模型，采用有限體積法，通過對不同空化數下，5種兩方程RANS方法湍流模型的空泡長度、徑向最大寬度等形態參數數值計算結果與經驗公式比較，提出了準確的超空泡航行體CFD數值計算方法。在建立準確數值計算模型基礎上，對超空泡流場特性進行了分析，為超空泡航行體設計提出了改進意見，凸顯了CFD優勢。

1 數值計算方法

1.1 基本數學模型

雷諾平均模型，是將瞬時的Navier-Stokes方程求解變量分解成平均的(時間平均和總體平均)和波動的分量。速度分量為：

(1)

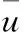
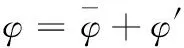
(2)

式中φ可以為壓力、能量或者組分濃度。

將以上兩公示的表達形式帶入瞬時的連續性方程和動量方程，同時取時間平均和總體平均的動量方程，得到了如下的笛卡爾坐標形式的雷諾平均Navier-Stokes方程。

(3)

(4)

本文選擇基于Rayleigh-Plesset方程的Schnerr and Sauer空化模型，考慮氣泡的生長和潰滅，氣液兩相輸運方程為：

(5)

其對應的蒸發和凝結速率可分別表示為：

(6)

(7)

其中：pc為水的飽和蒸汽壓，取3 169 Pa；Cprod、Cdest分別取1、2。

氣泡半徑R通過下式計算：

(8)

1.2 RANS兩方程模型

1) Standardk-ε模型

標準k-ε模型的湍動能k和湍動耗散率ε可以通過以下兩式進行計算。

(9)

(10)

(11)

式中，Gk表示平均速度分量產生的湍動能；Gb表示由于浮力作用所產生的湍動能；YM表示可壓縮湍動流中由于脈動膨脹所產生的湍動能量耗散；C1ε=1.44、C2ε=1.92、Cμ=0.09σk=1.0、σε=1.3為常數，Sk和Sε為自定義源項。

2) RNGk-εModel

RNGk-ε模型的輸運方程與標準k-ε模型相同。湍動黏性滿足：

(12)

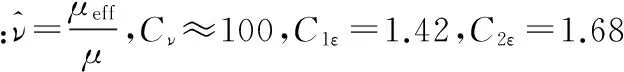
3) Realizablek-ε模型

Realizablek-ε模型的輸運方程為：

(13)

(14)

4) Standardk-ω模型

Standardk-ω模型的湍動能k和湍動耗散率ω可以通過下列公示確定。

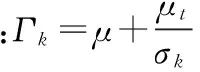
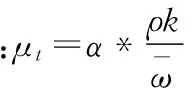
(17)

5)Shear-StressTransport(SST)k-ω模型

SSTk-ω模型的輸運方程與Standardk-ω方程相同。湍動黏性通過以下計算。

(18)

其中S是應變率的大小，并且：

1.3 研究對象和計算條件

本文選取文獻[5]中給出的無尾翼魚雷模型(如圖1所示)，進行超空泡航行體數值計算方法的研究。主要包括圓盤空化器、尾噴管、錐柱段彈體。主要幾何尺寸：空化器直徑(Dn)為10 mm，模型總長(Ln)520 mm，最大直徑為38 mm，尾噴管直徑19 mm。目前在對超空泡航行體CFD模擬，該模型應用廣泛、方法成熟、試驗技術成熟，許多專家、學者都以此為對象進行超空泡的探索、研究。

基于以上幾何模型，利用ICEM軟件，建立標準的三維結構化網格，對圓盤空化器入口表面、側面以及錐段體等進行局部加密。

計算域的進口采用速度入口，通過入口速度的改變實現空化數的調整。出口采用壓力出口，遠場采用固壁邊界條件。使用SIMPLE壓力-速度耦合項，采用標準的壓力離散格式，其余均采用一階迎風格式。

圖1 幾何模型

1.4 數值離散方法

在計算流體流體力學數值仿真過程中，作為前處理的數值離散方法的準確性對數值計算結果準確性至關重要。通常，由于網格之間在數值傳遞的過程中存在截斷誤差，而劃分網格的類型和網格生成的數量直接決定了誤差的大小。理論上，為了提高計算精度，降低誤差增加網格密度。但是考慮到計算機的計算開銷，在滿足誤差要求的前提下，盡可能降低網格的密度，突顯CFD的優勢。

目前主要通過劃分結構網格和非結構網格進行數值離散，非結構網格雖然前處理過程簡單、易實現，但是計算收斂耗時長，對于精細流場問題的處理準確度低。本文選用結構化網格劃分方法，具體劃分結果如表1所示。

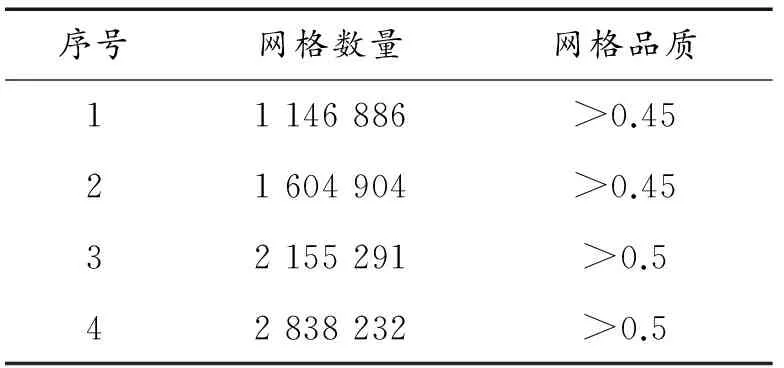
表1 網格劃分結果

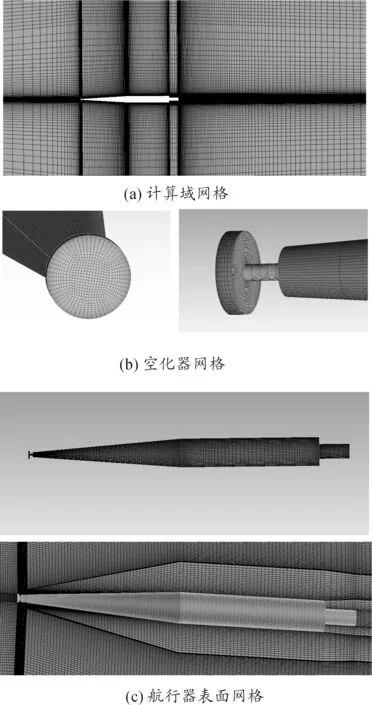
圖2 160萬網格數目時，網格劃分結果

2 計算結果及分析

2.1 網格密度對計算結果的影響

計算得到了不同空化數下，航行體形成超空泡的長度和最大截面寬度值。由圖3和圖4可知，網格密度為114萬時，空泡長度低于其他網格密度，空泡的寬度值更加明顯。160萬網格密度和215萬網格在計算空泡長度和空泡最大截面寬度值相差不大，網格密度為280萬時，當空化數大于0.02時精度明顯更高。因此，考慮到計算機的消耗機時和數值精度，在后續數值計算中選取網格密度為160萬，同時限定空化數小于0.02，確保計算精度。

圖5給出了空化數為0.01時，超空泡航行體的速度場分布圖，在空泡內部蒸汽相的速度為0，而超空泡所產生的尾流影響非常明顯，可以延伸很遠，所以在做非定常工況數值模擬的過程中，應增加航行體尾流區域計算域的尺寸。

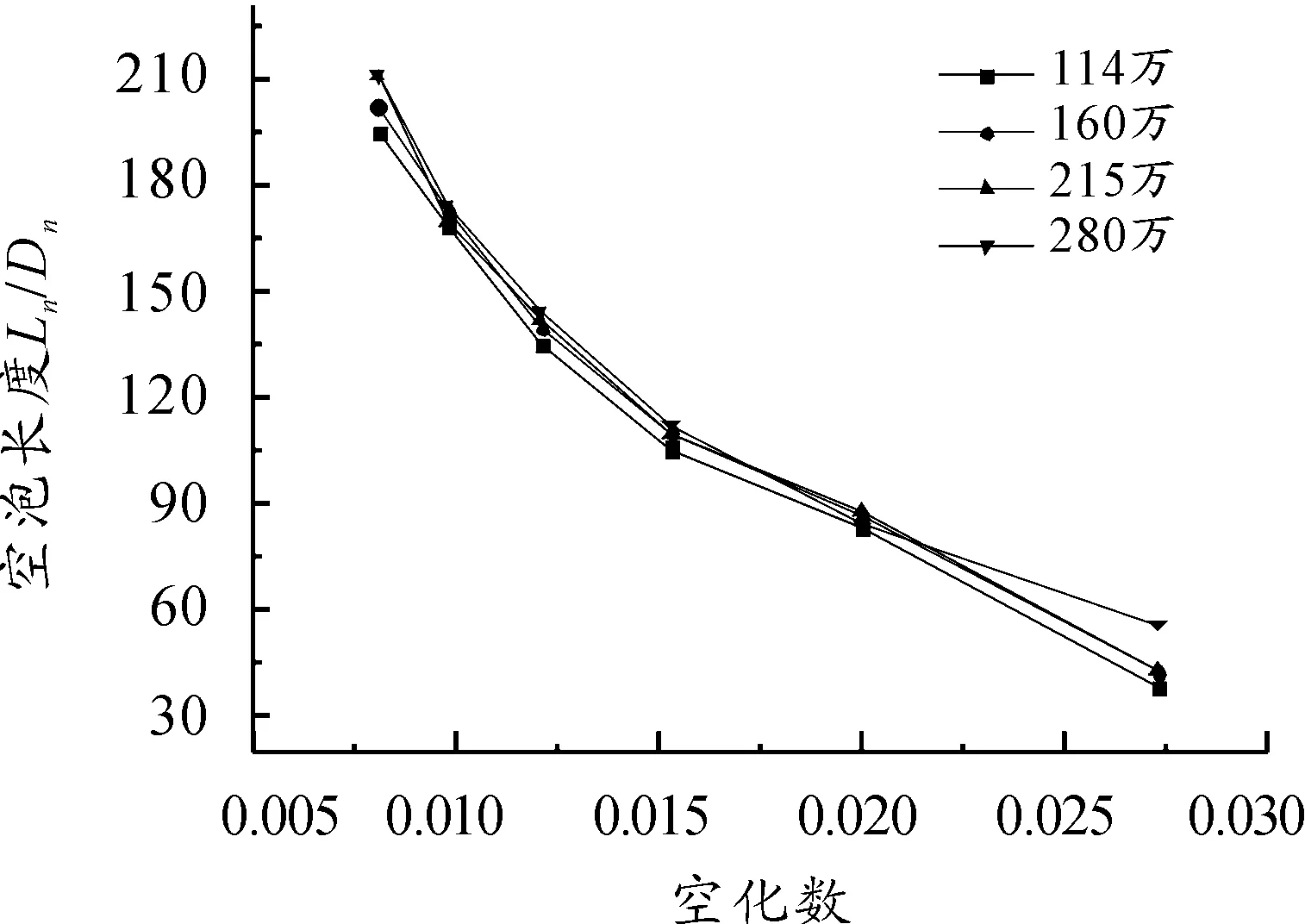
圖3 空泡長度隨空化數的變化

圖4 空泡寬度隨空化數的變化

圖5 流場速度分布示意圖

2.2 數值計算結果驗證方法

為了驗證選取數值計算方法的準確性，本文選取了烏克蘭國家科學院IHM積累的帶圓盤空化器模型自由運動的空泡形狀計算公式

(19)

(20)

以及Logvinovich的空泡截面獨立擴張原理式。Logvinovich在文獻[6]中給出了空泡的最大半徑和半長的半理論、半經驗計算公式，本文取空泡全長和最大截面直徑，將其修正如式(21)、式(22)所示。

(21)

(22)

通過計算可知，式(19)的計算結果和式(21)對空泡最大截面計算值相差最大可以達到11.77%，對于空泡長度的計算值相差可以達到23.32%。然而，烏克蘭國家科學院IHM的經驗公式是建立在大量水洞和敞水試驗基礎上的，而Logvinovich空泡截面獨立擴張原理又是目前公認的描述超空泡流最為準確的計算方法。因此，為了得到較為準確的驗證結果，利用數值優化軟件，對上述公式分別進行6次多項式數值擬合，確定系數R分別為0.994 14和0.999，擬合得到無量綱空泡最大截面直徑Dc/Dn計算式和無量綱空泡長度Lc/Dn計算式如下，其結果分別如圖6、圖7所示。

圖6 Dn/Cn的擬合結果

(23)

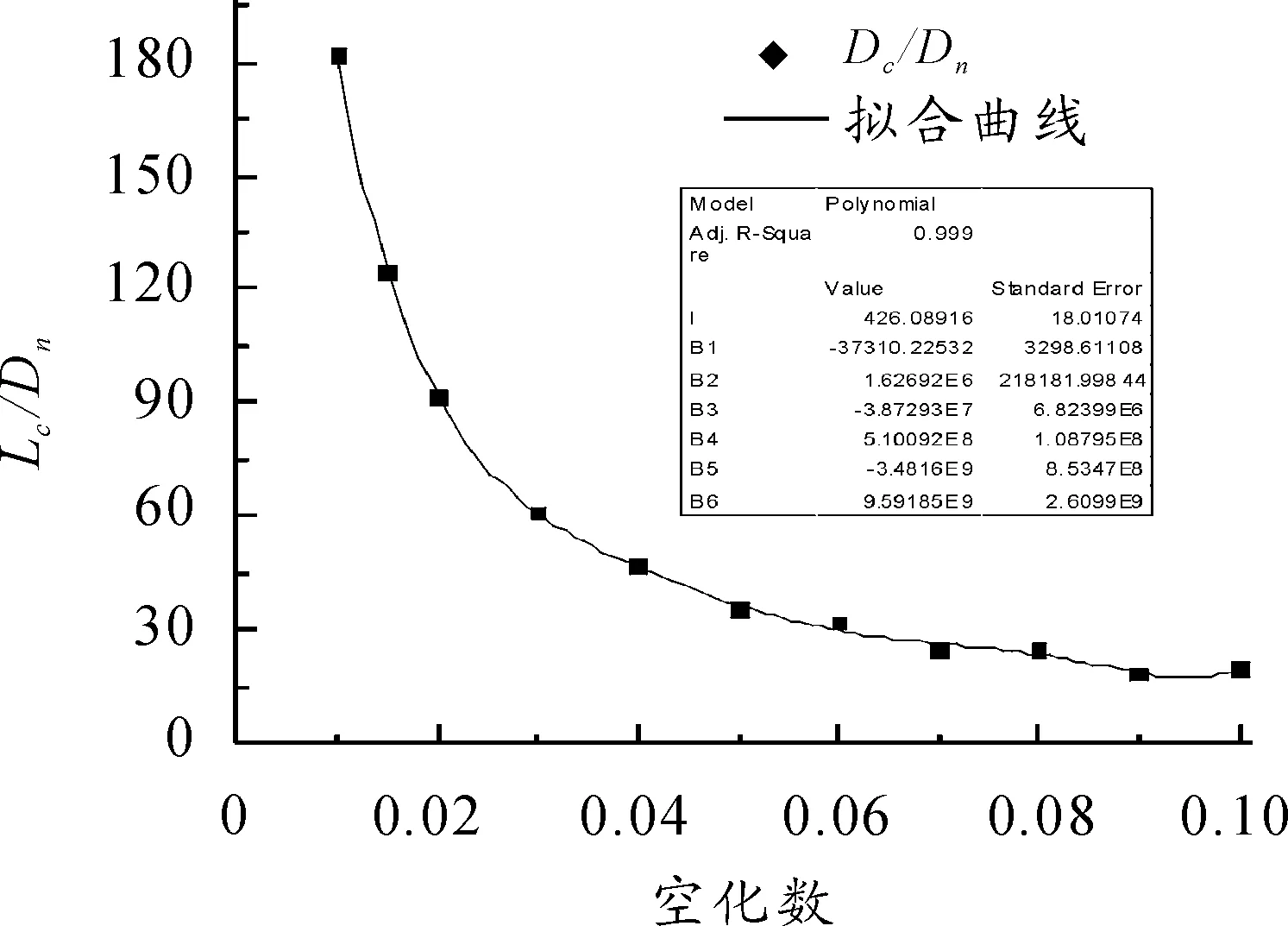
圖7 Ln/Dn的擬合結果

(24)

通過將CFD軟件計算得到的空泡形態參數與擬合得到的結果(式(23)和式(24))進行對比，得到數值計算誤差，進而確定準確的數值計算模型。

如表2和表3給出了擬合結果與烏克蘭國家科學院IHM的經驗公式與Logvinovich空泡截面獨立擴張原理關于空泡形態計算公式的計算結果對比，表明擬合結果關于無量綱空泡最大截面直徑Dc/Dn的誤差均小于8%，關于無量綱空泡長度Lc/Dn計算結果的誤差小于11%。通過計算結果與擬合結果進行對比，充分考慮了兩類經驗公式優勢：試驗數據豐富、理論完善，得到新的空泡形態計算公式可信度更高，數值計算驗證方法也更為準確。

表2 Dc/Dn擬合結果與經驗公式比較

表3 Lc/Dn擬合結果與經驗公式比較

2.3 空泡形態計算結果分析

對于超空泡航行體的數值模擬，由于涉及大量氣液質量傳輸過程，所以數值模擬復雜程度較高，計算準確性難以把握。

表4給出了不同兩方程模型下的數值空泡截面寬度的無量綱數值計算結果。從表中可以看到，數值計算得到的結果均小于由擬合經驗公式計算得到的結果。圖8給出了不同計算模型下空泡截面寬度的計算誤差隨空化數的變化關系，當空化數小于0.02時，數值模擬的精度較高，Kω-Sst模型的計算結果誤差基本上小于14%，相對其他計算模型準確度更高。

表4 Dc/Dn擬合結果與經驗公式比較

由于本文中，設計數值試驗為敞水試驗工況，而經驗公式的試驗值及理論結果大部分均來源于水洞試驗，計算結果受水洞影響較大。實際中，由于存在靜水壓力，對空泡截面寬度影響較大。所以，計算結果與經驗公式存在一定誤差。從圖8可見，空化數在0.015～0.02時數值計算結果受其他因素影響較小，計算精度可以達到小于9%。

圖8 空泡截面寬度計算結果誤差對比

表5給出了不同RANS兩方程模型空泡長度的無量綱(Lc/Dn)計算結果，不同計算模型下，空泡長度的計算結果均小于經驗公式的計算值。相同空化數下，不同模型計算結果相差不大。圖9比較了不同湍流模型空泡長度計算誤差隨空化數的變化結果，由圖可見，在空化數小于0.01時，Kω-Sst模型和Kω-Stan模型的計算準確性較高，計算誤差小于4%，當空化數大于0.01小于0.02時，Kω-Sst模型計算精度相比其他模型較高，可以保證小于8%。

表5 不同RANS模型空泡長度的無量綱計算結果

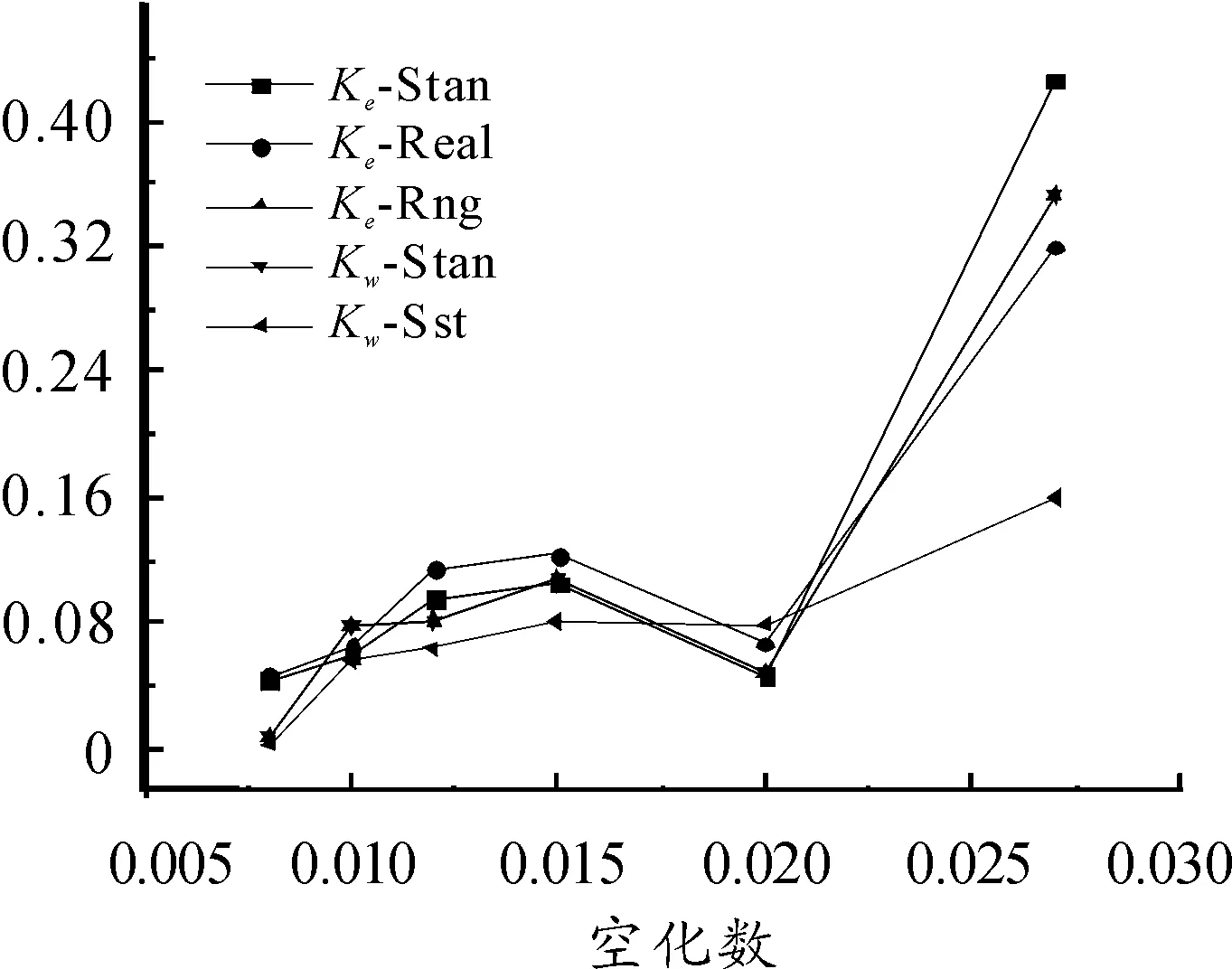
圖9 空泡長度計算結果誤差對比

比較不同RANS兩方程空泡最大截面寬度的計算結果和空泡長度的計算結果可知，Kω-Sst模型更適用于超空泡航行體的數值模擬。

2.4 流場特性分析

基于建立文中確定的數值計算模型，選取精確度較高的Kω-Sst模型，水深10 m，空化數為0.015時，對超空泡航行體進行流場特性研究。

圖10給出了超空泡航行體的艏部的空泡相分布云圖和速度場云圖，從圖中可以得到當水在空化器銳緣附近汽化后流入超空泡內部，在空化器后部速度會急速增加達到100 m/s量級，在航行體艏部附近還存在一定的速度梯度，該速度梯度以及高速氣流的存在嚴重影響超空泡的穩定性，對超空泡航行體的穩定運行造成影響，在超空泡航行體的設計中需要改良空化器或者優化航行體艏部形狀，消除該速度梯度和高速氣流區。

圖10 超空泡航行體頭部相分布云圖(上)和速度場云圖(下)

圖11給出了超空泡航行體的壓力場云圖。從圖中可見，由于無尾翼超空泡航行體在自然超空泡航行過程中只有艏部空化器與水接觸，艏部空化器在空化數為0.015時需要承受壓力為123個大氣壓。因此在對空化器設計的過程中，需要充分考慮承受壓力對空化器的影響，盡可能地增大受壓面積，采用高抗壓材料，保證水下超空泡航行體運行安全。

圖11 空化數為0.015時，超空泡航行體的壓力場

圖12給出了超空泡航行體的渦流強度分布，由計算結果可知，航行體尾部渦強度較大，在艏部區域以及尾流區域，渦通量達到最大。由于渦強分布，可以得到旋渦作用強度分布，進而可以定性的得到超空泡航行體運動過程中所受到的擾動作用強弱。

圖12 超空泡航行體的渦流強度分布

3 結論

1) 基于烏克蘭國家科學院IHM半經驗公式和Logvinovich空泡截面獨立擴張原理式，利用數值優化方法，建立了空泡形態數值計算驗證模型。

2) 比較了RANS兩方程模型對超空泡航行體數值計算結果，得到了Kω-Sst模型的關于空泡最大截面計算結果誤差小于14%；對空泡長度的數值計算結果小于8%，空化數小于0.01時，小于4%。

3) 基于建立的準確性數值模型，對空化數為0.015時自然超空泡進行了流場分析，為超空泡航行體空化器的設計提出了改進意見。

[1] WEILAND C,VLACHOS P.Observation of a Critical Time Scale for Supercavi-tation Development and the Effect of Gas Leakage[C]//2008 ASME Fluids Engineering Conference.Florida USA,2008.

[2] 李鳳臣,鄒志林,蔡偉華,等.減阻劑水溶液內彈體入射超空泡特性實驗研究[J].工程熱物理學報,2010,31(5):857-862.

[3] WU T Y.A Free Streamline Theory for Two-Dimensional Fully Cavitated Hydrofoils[J].Journal of Mathmatical Physics,1956:236.

[4] SINGHAL A K,LI H Y,ATHAVALE M M,et al.Mathematical Basis and Validation of the Full Cavitation Model[C]//ASME FEDSM’01.New Orleans,Louisiana,2001.

[5] SEREBRYAKOV V V.Ring Model for Calculation of Axisymmetric Flows with Developed Cavitation[J].Journal of Hydromech,1974(27):25-29.

[6] SEREBRYAKOV V V.Some Models of Prediction of Supercavitation Flows based on Slender Body Approximation[C]//Proceedings of the Fourth International Symposium on Cavitation.Pasadena,USA,2001:sessionB3.001.

[7] 高強,張宇文,陳偉政.基于細長體理論的超空泡外形估算[J].彈箭與制導學報,2005,25(2):373-376.

[8] QIAN ZHONGHUA,HUANG SHEHUA.Comparison and analysis of computed results for cavitating flow with four turbulence models[J].Advances in Water Science,2006,02:203-208.

[9] HU QINGQING.Experimental Observation And Numerical Calculation Of Supercavity Flow Of Blunt Body Under Different Inclination Angle Into The Water[D].Zhe jiang:Zhe jiang Sci-Tech University,2014.

[10]XING YANJIANG.Research on hydrodynamic characteristic of vehicle unsteady cavity flow[D].Harbin:Harbin Institute of Technology,2013.

[11]趙怡，劉平安，苗成林.非穩態超空泡流動的數值模擬[J].四川兵工學報，2015(1): 64-67．

(責任編輯 楊繼森)

Supercavitation Research on Numerical Simulation Method Based on Two-Equation RANS Model

DU Pei-pei, XIAO Chang-run, ZHANG Lu, ZHENG Wen-long, JIAO Yu-chao

(Department of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, China)

In order to get the accurate numerical simulation method, the calculation model of supercavity shape was established based on the semi-empircal formula of supercavity form in Institute of Hydromechanics of National Academy of Science in Ukraine and the Logvinovich principle of independent expansion of cavity section. By using the finite volume method, the nelerical discretization method of supercavitation flow was authenticated and the supercavitation flow with five different two-equation RANS model was calculated in different cavitation number. The simulated results indicate that the accuracy of the calculation results ofKω-Sstis higher compared with other models. The complutational error of the dimensionless maximum diameter of the supercavity can be maintained at less than 14%. And the calculation error of the cavity length can be reduced to less than 8% and the error can be futher reduced to 4% when the cavitation number is less than 0.01. Based on the established mathematical model, the flow performance of the supercavitation vehicle was calculated when the cavitation number is 0.015. The computed and analyzed results show that: there is a high-speed air flow area and obvious velocity gradients behind the cavitator. Hydrostatic pressure in the vicinity of cavitator can reach 123 atomosphere pressures and the improvement of the design of the supercavitation vehicle is proposed based on these calculation results.

supercavitation；turbulence model；finite volume method；CFD

2016-06-16；

2016-07-15

國家部委基金資助項目(51314010203)

杜佩佩(1991—)，男，碩士研究生，主要從事艦船流體力學研究。

肖昌潤(1963—)，男，博士，副教授，E-mail：xiaochangrun@sina.com。

10.11809/scbgxb2016.10.037

杜佩佩，肖昌潤，張露，等.基于RANS方法超空泡流數值計算方法研究[J].兵器裝備工程學報，2016(10):174-180.

format:DU Pei-pei, XIAO Chang-run, ZHANG Lu,et al.Supercavitation Research on Numerical Simulation Method Based on Two-Equation RANS Model[J].Journal of Ordnance Equipment Engineering,2016(10):174-180.

TJ610.1

A

2096-2304(2016)10-0174-07