高速火箭彈不同防熱方案對氣動加熱影響規律的研究

周宇航，張向洪，張 敏

(南京理工大學 能源與動力工程學院，南京 210094)

?

【裝備理論與裝備技術】

高速火箭彈不同防熱方案對氣動加熱影響規律的研究

周宇航，張向洪，張 敏

(南京理工大學 能源與動力工程學院，南京 210094)

采用工程算法與數值算法相耦合的氣動熱計算方法進行高超聲速火箭彈的氣動熱參數計算。對火箭彈邊界層外緣參數采用無黏數值算法求取，對邊界層內黏性起主導作用的區域采用工程算法計算。由于防熱層厚度方向特征尺寸遠小于火箭彈表面特征尺寸，對防熱層的氣動熱計算進行了一維簡化并建立了一維非穩態導熱微分方程。在確定防熱層邊界條件后，經過導熱微分方程的求解得到了長航狀態下火箭彈防熱層的溫度分布。通過對防熱層的不同物性參數的研究，得出防熱層物性參數對氣動加熱的影響規律，為氣動熱防護問題的研究提供了參考。

防熱層；數值算法；工程算法；高超聲速；氣動熱參數

隨著科學技術的迅猛發展，高新技術在兵器研制中得到廣泛應用，武器的性能獲得大幅度的提高，獲得戰爭的勝利不再是取決于武器數量的多少，更多的是取決于武器質量優劣[1-3]。高超聲速火箭彈一般是指以吸氣發動機或組合發動機為動力，在大氣層內和跨大氣層中飛行速度大于5馬赫的火箭彈，高超聲速武器是當今世界主要軍事強國發展的重點[4-6]。

高超聲速火箭彈的氣動特性、氣動加熱和大氣干擾會引起基礎結構失真、模型和參數不確定等一系列問題。高超聲速飛行對火箭彈的氣動性能以及防熱提出了更高的要求[7]，對此承擔著火箭彈氣動熱防護主要任務的防熱層起著至關重要的作用。而防熱層的物性參數選取直接決定了防熱層的熱防護效率，本研究對防熱層的不同物性參數進行研究，得出不同物性參數對氣動加熱的影響規律。

高超聲速火箭彈在飛行過程中表面溫度隨著時間的推進不斷增加直至進入熱穩態。對于高超聲速飛行器進入穩態狀況后，熱流密度越大的區域溫度越高，并在駐點達到溫度最大值。由于駐點溫度很高極易產生燒蝕影響火箭彈的穩定飛行，因此在火箭彈表面添加防熱層可以延緩表面的溫度升高速率，延長火箭彈達到熱穩態的時間。防熱層不同的物性參數材料的選取直接決定了火箭彈的溫升速率。本文采用數值算法與工程算法相耦合的計算方法求解火箭彈表面的氣動熱參數[8]。在火箭彈表面的氣動熱參數確定后，采用非穩態導熱微分方程的中心差分格式計算長航狀況下防熱層溫度分布。根據非穩態狀況防熱層的溫度分布分析物性參數對氣動加熱的影響[9-10]。

1 高超聲速火箭彈表面和防熱層氣動熱參數計算方法

工程計算中將火箭彈表面氣動熱分為兩部分：一部分為非駐點區域氣動熱計算，由于對火箭彈模型進行了簡化，本文采用平板熱流密度公式進行非駐點區域氣動熱計算；另一部分為駐點區域氣動熱計算，采用Fay-Riddell駐點熱流密度計算公式計算駐點熱流密度[11]。

本文邊界層外緣無黏區域數值計算，邊界層內黏性主導區域采用工程算法計算火箭彈表面氣動熱參數[12]。在計算防熱層溫度分布前，對火箭彈物理模型進行簡化：因為防熱層的厚度尺寸遠小于飛行器物面尺寸，將整個火箭彈防熱層看作一維平板。對于一維平板非穩態導熱，采用一維非穩態導熱微分方程的中心差分格式計算長航狀況下防熱層溫度分布[13-14]。

1.1 駐點氣動熱分析

火箭彈在飛行過程中前緣出現速度為零且靜壓達到最大值的點，在空氣動力學上叫做駐點。由于駐點處氣流壓縮現象最為強烈，往往形成劇烈的氣動加熱，因此駐點的氣動熱計算和分析至關重要。依據駐點的定義通過如下的算法確定駐點位置：對于四邊形網格，通過Fluent求解器輸出的格點速度矢量求解出兩個格點所在邊的速度矢量，同理確定剩余邊的速度矢量。對于四邊形網格，若四條邊界上的速度方向都指向四邊形外側，那么這個點可以判斷為駐點。駐點熱流密度與邊界層外緣參數的關系為

(1)

式中：Pr為普朗特數，取0.7；Le為路易斯數，取1.4；Rn為研究對象的球頭半徑；(due/ds)s為駐點處速度梯度；hD為空氣平均離解焓。

1.2 平板氣動熱計算

高超聲速火箭彈非駐點區域的傳熱系數計算，目前主要通過經驗公式計算并加以修正[14]。對于可壓縮流首先轉換簡化為不可壓縮流求解，再通過雷諾比擬把斯坦頓數和表面摩擦因數聯系起來轉換到可壓縮流[15]。對于壓縮效應，采用Eckert參考焓進行修正。從而得到了平板氣動熱的求解公式

(2)

式中： ρe為邊界層外緣密度； μe為邊界層外緣速度； ρ*、 μ*在得到參考焓后根據氣體熱力學特性求出。

在整個火箭彈表面的熱流密度確定后，在非穩態狀況下防熱層內部邊界條件為絕熱邊界條件，防熱層外部邊界條件為熱流邊界條件，可以進行火箭彈的防熱層導熱計算。

1.3 防熱層的氣動熱參數計算

根據能量守恒定律與傅里葉定律建立物體的溫度場應當滿足的關系式稱之為導熱微分方程。導熱微分方程是滿足所有導熱物體的通用方程

(3)

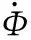
(4)

式中α=λ/ρc稱為熱擴散率或熱擴散系數。在簡化了導熱微分方程后，采用有限差分方法求解防熱層溫度分布。首先對平板的厚度L方向進行離散化，得到

(5)

Δx=xi+1-xi作為空間步長，顯然xi=(i-1)Δx。

對于時間離散采取同樣的離散方式。為了區別于空間步長，這里使用n作為標示。

(6)

時間步長Δτ=τn-τn-1，顯然τn=nΔτ。

將式(4)用于平板i點上第n時刻，可以得到

(7)

對于左側非穩態項用一階差分，對于右側擴散項采用二階中心差分有

(8)

整理后有

(9)

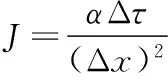
(10)

經過上述推導，得到了下一個時刻節點溫度與上一時刻節點溫度關系，當時間條件與邊界條件得到確定后就可以得出整個防熱層的溫度分布。

對于具體的問題，還需要確定相應的時間條件與邊界條件以滿足方程的求解。對于防熱層導熱計算，本文使用的初始時間條件T(x,0)為已知定值。邊界條件為第二類邊界條件，即熱流邊界條件。防熱層外緣的熱流q1為平板熱流密度，即q1=qw。平板內側的熱流密度q2在非穩態情況下，假設為q2=0。將邊界條件應用于傅里葉導熱定律，則每一時刻邊界溫度有如下關系。

(11)

2 高超聲速火箭彈表面氣動熱參數的算例驗證

本文使用D-5450鈍錐模型，對飛行器表面氣動熱參數進行驗證。

在NASA TN D-5450報告中，Joseph W.Cleary等做了一系列風洞實驗，并整理了15度的鈍錐層流熱流密度，在這里選取該模型進行算例驗證。設置求解條件，飛行狀態為零攻角，大氣壓p∞=132 Pa，空氣溫度T∞=47.34 K，來流空氣速度Ma∞=10.6。該模型尺寸如圖1所示。

圖1 模型尺寸

在確定了求解對象后，進行網格的劃分。網格劃分決定了在Fluent求解器的求解精度。本文劃分的網格有節點9 594個、四面體單元9 321個。由于求解對象的外形決定頭部氣動加熱最為明顯，所以在劃分網格時對研究對象的頭部網格密度加大，保證了頭部所得解的精度。劃分完成后的網格示意圖如圖2。

圖2 彈體網格和頭部網格

將網格輸入至Fluent求解器，按上述求解條件設置參數，得到收斂結果如圖3和圖4所示。

圖3 鈍錐壓力云圖

圖4 鈍錐密度云圖

圖中較清晰地捕捉到了弓形脫體激波。由壓力分布可以看出頭部的壓強急劇上升，空氣在頭部區域速度很低。彈身壓力很小較頭部相差兩個數量級。由密度分布可以清楚的看到在彈頭和彈身流場的激波，且彈體的激波層的厚度尺寸與彈體的特征尺寸相比要小很多。

通過Fluent求解器獲取到邊界層外緣的氣動熱參數，將駐點區域邊界層外緣參數代入Fay-Riddle駐點熱流密度計算公式計算熱流密度qws，非駐點區域代入平板熱流密度公式求解平板熱流密度qw。求得的熱流密度與NASA對D-5450 的實驗結果和純數值對D-5450算法的純數值計算進行對比，說明耦合算法的可行性。

坐標軸橫坐標表示彈體上一點的特征尺寸與彈體特征長度的比值，縱坐標表示彈體的熱流密度與實驗駐點熱流密度qws=2.65×105W/m2的比值。工程算法的駐點熱流密度qws=356 328 W/m2，耦合算法求得的駐點熱流密度qws=358 902 W/m2相對誤差為0.007，說明所采用的方法與純工程算法具有相同的精度，非駐點區域熱流與實驗值吻合較好。數據對比如圖5所示。

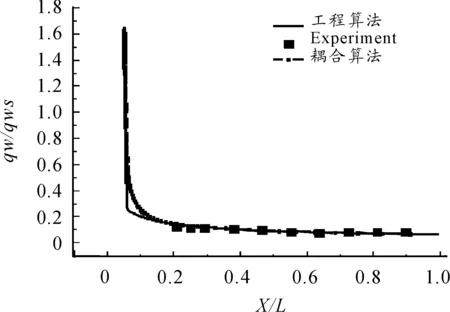
圖5 鈍錐模型頭部計算結果

3 帶防熱層的復雜外形彈箭的氣動熱研究

通過D-5450算例證明了可以較為精準的為氣動熱防護問題提供數值計算。本文研究對象為圖6所示的復雜外形彈箭。

上述的壓力和密度云圖可以清晰地捕捉到脫體激波，壓強和密峰值出現在頭部。根據這些現象，說明本文的數值算法求解邊界層外緣參數基本符合物理解。將邊界層外緣參數導入到本文的工程計算方法得到彈體表面的熱流密度分布如圖8所示。

圖6 彈體與對稱面網格

彈體在初始時刻熱流密度最大值和最小值分別為1.4×106W/m2、16 923 W/m2，彈體在50 s時熱流密度最大值和最小值分別為3×105W/m2、12 697 W/m2。在彈體表面的熱流密度和彈體最內層熱流密度確定后，邊界條件得到確定，可以進行平板的非穩態導熱求解。基于非穩態導熱微分方程可求得經過一次時間步長后彈體的溫度分布。再將最外層表面溫度代入平板熱流密度公式，求得新的熱流密度，再代入導熱方程進行溫度求解，以此類推進行循環。每次循環時間為一個時間步長，當時間步長滿足迭代條件時可以輸出彈體溫度分布結果。

圖7 彈體密度與壓力云圖

圖8 彈體表面熱流密度

本文選用3種材料作為三層防熱層的涂層，由外至內分別為防熱層1、主防熱層2、防熱層3，厚度分別為5 mm、20 mm、5 mm。本文提出不同的方案研究防熱層的溫度，在長航情況下監測不同時刻防熱層不同位置的溫度T1、T2、T3、T4(T1、T2、T3、T4分別為最外層的點、第一層與第二層交界點、第二層與第三層交界點、最內層點)。

本文的防熱層材料的物性參數如表1所示。

表1 防熱層物性參數

方案1：SiC、C/SiC、Al2O3分別為防熱層1、主防熱層2、防熱層3。經過計算后的各個時刻不同點的溫度分布如圖9所示。

在方案1中共有4個不同時刻的防熱層不同監測點的溫度分布，可以看出隨著飛行時間的增加，最外層溫度T1在20 s很快上升至1 000 K且在后續的飛行過程溫度提升很小，而防熱層內部溫度T2、T3、T4分布呈現線性增長的趨勢。說明了熱流是由外往內傳遞，且最外層的氣動加熱很快趨于最大值，內部的溫升主要是由防熱層的熱傳導決定。

方案2：Al2O3、C/SiC、SiC分別為防熱層1、主防熱層2、防熱層3。經過計算后的各個時刻溫度分布如圖10所示。

方案2是將方案1的第一層與第三層進行交換，材料的選擇和厚度與方案1保持一致。SiC的導熱系數為Al2O3的3.5倍，由方案2的溫度分布可以看出同熱流密度情況下，導熱系數越大溫差越小。因此同熱流密度下最外層材料的導熱系數越大，T1的溫度越低。

方案3：Al2O3、3Al2O3·2SiO2、SiC分別為防熱層1、主防熱層2、防熱層3。經過計算后的各個時刻溫度分布如圖11所示。

在方案3中將主防熱層2采用為比C/SiC熱擴散率更大的3Al2O3·2SiO2。由方案3各個時刻溫度分布可以看出同一時間差情況下，熱擴散率α越大防熱層節點溫度越高，即熱擴散率越大下一時刻的節點溫升越大。通過方案3與方案2的對比，方案3在50 s長航狀況下最內層T4的最大值比方案2的最大值要高90 K，說明了熱擴散率越大節點溫升越高。

方案4： SiC、3Al2O3·2SiO2、Al2O3分別為防熱層1、主防熱層2、防熱層3。經過計算后的各個時刻溫度分布如圖12所示。

經過4種方案的對比，本文給出了防熱層的溫度分布的兩個主要影響因素：最外層的導熱系數和主防熱層的熱擴散率。最外層的導熱系數越大防熱層的熱防護效果越好，最外層溫升越慢。主防熱層的熱擴散率越大防熱層的熱防護效果越差，整個防熱層的溫升越快。

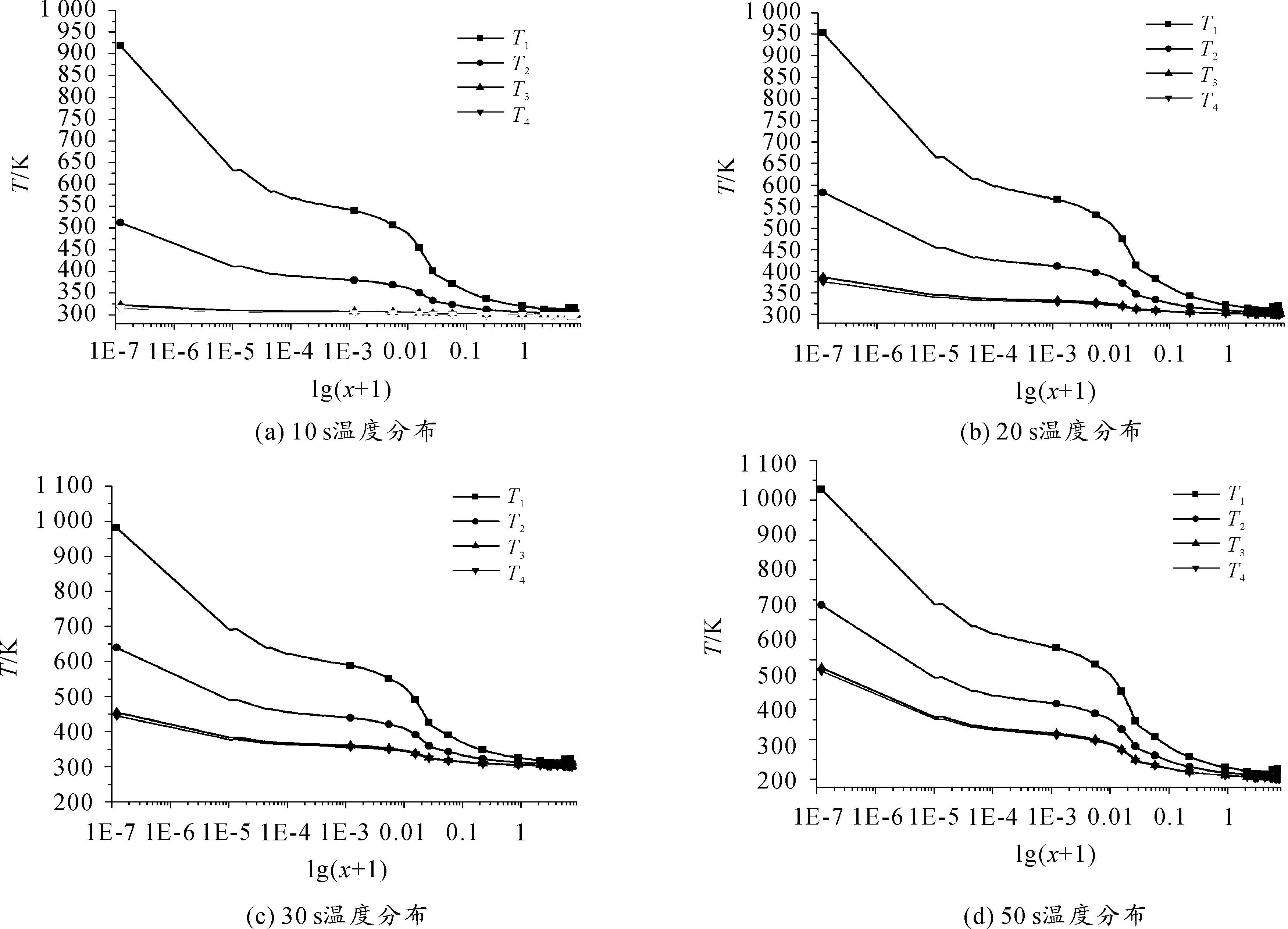
圖9 方案1溫度分布

圖10 方案2溫度分布

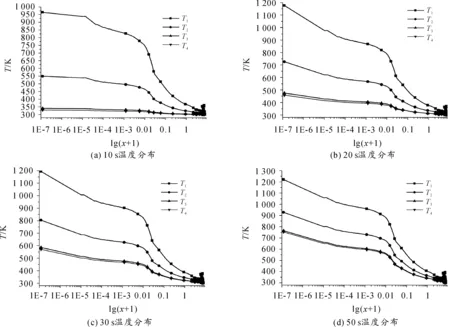
圖11 方案3溫度分布

圖12 方案4溫度分布

4 結論

本文采用耦合算法對D-5450鈍錐算例進行了驗證，在驗證了算法的準確性后，對復雜外形火箭彈的防熱層溫度分布進行了研究，給出了物性參數對溫度分布的影響。得出的主要研究結論有如下幾點：

1) 同一時刻下，通過防熱層最內層與最外層的溫度對比，說明了火箭彈在添加防熱層后能有效地延緩熱量向火箭彈傳遞，降低了火箭彈的溫度，保護火箭彈不受高溫影響。

2) 通過選取不同的材料，研究防熱層的溫度分布，得出了防熱層物性參數對彈體氣動加熱的影響規律，即：最外層導熱系數越大，防熱層防熱效率越高，溫度越低；主防熱層熱擴散系數越低，防熱層防熱效率越高，溫度越低。

本文對于防熱層的氣動熱分析僅僅進行了零功角的分析，未考慮高超聲速火箭彈的復雜飛行狀況，因此在后續開展的工作中將研究不同功角下火箭彈的防熱層氣動加熱。

[1] 王國雄.彈頭技術(上)[M].北京：中國宇航出版社，2005.

[2] 李惠峰，余光學.近空間高速飛行器多模型最優控制器設計[J].Proceedings of the 31stChinese Control Conference,2012：864-869.

[3] 姜貴慶，劉連元.高速氣流傳熱與燒蝕熱防護[M].北京：國防工業出版社，2003.

[4] 張志成.高超聲速氣動熱和熱防護[M].北京：國防工業出版社，2003.

[5] 李惠峰.高超聲速飛行器制導與控制技術(上)[M].北京：中國宇航出版社，2012.

[6] 錢翼稷.空氣動力學[M].北京：北京航空航天大學出版社，2004.

[7] FRED R.DEJARNETTE.A Review of some Approximate Methods Used in Aerodynamic Heating Analyses[J].Journal of Thermophysics and Heat Transfer,1985,1(1):5-12.[8] JOHN D.ANDERSON,JR.Hypersonic and high temperature gas dynamics[M].USA:McGraw-Hill BookCompany,1989.

[9] 呂紅慶.高超聲速鈍頭體氣動熱分析[J].導彈與航天運載技術,2008,295(3):41-45.

[10]楊光達.基于軸對稱比擬的高超聲速復雜外形氣動熱預測方法研究[J].航空計算技術,2014,44(2):95-101.

[11]雷延花.高超音速飛行器氣動加熱計算[J].上海航天,2001,18(5):10-13.

[12]鄒小飛.再入彈頭氣動加熱及熱響應分析[D].長沙：國防科技大學,2009.

[13]馬繼魁.高超聲速鈍頭體表面熱流的數值模擬[J].科學技術與工程,2010,10(36):9019-9022.

[14]梁強,張平峰.基于CFD復雜外形飛行器氣動加熱高效算法[J].上海航天,2013,30(5):14-20.

[15]陳鵬.高速彈頭氣動熱工程算法與數值計算研究[D].南京：南京理工大學,2013.

[16]張志豪， 孫得川.飛行器氣動加熱燒蝕工程計算[J].兵工學報，2015(12):1949-1954.

(責任編輯 周江川)

Research on Different Plan of Heat Shield Impacting on Aerodynamic Heating

ZHOU Yu-hang, ZHANG Xiang-hong, ZHANG Min

(School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

This paper calculated thermal parameters of rocket using aerothermal calculation coupling engineering and numerical algorithms with hypersonic rocket. Inviscid numerical algorithm was adopted to obtain parameters of the outer edge of the boundary layer while engineering algorithm was used in the inner area of the boundary layer where the viscosity plays a leading role. Since the size of the thickness of the heat protection layer is much smaller than the one of the surface of the rocket, the aerodynamic thermal calculations of heat shield were simplified one-dimensionally in this paper which establishes differential equation of one-dimensional unsteady heat conduction. The temperature distribution of heat protection of rocket layer under the state long-endurance was obtained through solving differential equation of heat conduction. Physical parameters of the heat shield impacting on the aerodynamic heating were obtained through the study of regular pattern of the physical parameters of heat protection layer, which provides a reference for the study of aerothermal protection.

heat shield; numerical algorithm; engineering algorithm; hypersonic; aerothermal parameter

2016-06-11；

2016-07-09

十二五總裝預研項目

周宇航(1996—), 男, 碩士研究生, 主要從事氣動加熱方面研究。

10.11809/scbgxb2016.10.005

周宇航，張向洪，張敏.高速火箭彈不同防熱方案對氣動加熱影響規律的研究[J].兵器裝備工程學報，2016(10):24-30.

format:ZHOU Yu-hang, ZHANG Xiang-hong, ZHANG Min.Research on Different Plan of Heat Shield Impacting on Aerodynamic Heating[J].Journal of Ordnance Equipment Engineering,2016(10):24-30.

TJ415

A

2096-2304(2016)10-0024-08