基于改進粒子群算法的飛行器沖突解脫方法研究

甄 然，司 超，吳學禮，張建華，武曉晶

(1.河北科技大學電氣工程學院，河北石家莊 050018；2.河北省生產過程自動化工程技術研究中心，河北石家莊 050018)

?

基于改進粒子群算法的飛行器沖突解脫方法研究

甄 然1,2，司 超1,2，吳學禮1,2，張建華1,2，武曉晶1,2

(1.河北科技大學電氣工程學院，河北石家莊 050018；2.河北省生產過程自動化工程技術研究中心，河北石家莊 050018)

沖突解脫要求飛行器采用一種有效的方法來滿足工作環境的限制。針對飛行器在多障礙環境下的沖突解脫問題，提出一種能夠滿足限制條件的改進粒子群算法(PSO)對沖突進行解脫。所提出的新算法(DARPSO)相對于經典粒子群算法有2個優點：第一，考慮了障礙對尋優過程的影響；第二，具有跳出局部極小的能力。仿真實驗結果顯示，所提出算法的優化效果要優于標準粒子群算法。將改進后的算法應用到飛行器沖突解脫過程中并進行仿真，結果表明，所提出的算法能夠有效地指導飛行器躲避障礙，完成沖突解脫。

算法理論；飛行器；沖突探測；沖突解脫；粒子群算法

近年來，空中交通領域迅速發展，美國、日本等相繼設立相關組織來適應新的空中交通發展[1]。空中交通管理中的一個安全問題就是飛機的沖突探測和解脫。由于飛機軌跡預測的準確性受到一些不確定因素的影響，比如雷達、導彈、氣候等，所以，在沖突探測和解脫的過程中考慮障礙物等不確定因素的影響具有重要的意義[2-3]。

粒子群算法是基于種群優化的方法[4-7]，本文在粒子群算法的基礎上，提出一種新的粒子群算法來滿足沖突解脫過程中的限制條件，同時保持粒子間的多樣性及跳出局部極小值的能力。

1 粒子群算法及拓展

(1)

(2)

在PSO中，隨著每個粒子迭代速度的減小，會越來越接近0，這時所有的粒子會趨于一種平衡的狀態，這些粒子沒有足夠的能力去探索和開發新的空間，極易陷入局部最優的情況[8-10]。所以，基于PSO的方法都必須具備跳出局部極小的能力。

文獻[11—13]在PSO的基礎上進行了改進，提出了機器人粒子群算法 (robotic particle swarm optimization, RPSO)，筆者將算法應用到機器人探測未知路徑的過程中，并考慮了障礙對尋優過程的影響。RPSO類似PSO都是由一群粒子在未知空間中進行搜索[14-15]，那么，不同之處主要就是RPSO考慮了真實環境中的障礙回避。其他的不同點并不是很顯著，包括對參數的初始化設置等。在RPSO中，每個粒子的速度和位置更新公式如式(3)和式(4)所示：

(3)

(4)

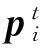
該算法在文獻[12]中的測試結果顯示，相對經典粒子群算法而言，RPSO能夠跳出局部極小值，但是效果不明顯。算法引入了約束條件對粒子的動作進行限制，這種方法能夠基本保證算法在搜索過程中粒子的多樣性，但仍存在收斂速率慢等問題。

文獻[16]中提出了一種動態自適應的粒子群算法(DAPSO)，該方法將慣性權重改為具有動態特性的時變參數。DAPSO中粒子的速度和位置更新公式如式(5)和式(6)所示：

(5)

(6)

對比經典粒子群算法，DAPSO的速度更新公式(5)有2個顯著的優點，隨機數r1和r2的取值隨著粒子數量和迭代次數隨機改變，慣性權重的取值也受到粒子的數量和迭代次數的影響。并且在動態慣性權重改變的過程中引入了2個新的概念，分別是“進化速度”和“聚集度”，這2個因素在文獻[17]中有介紹。通過引入這些新的概念，使算法跳出局部極小值的能力和算法收斂速度及精度有了顯著的提升。

2 具有動態自適應特性的機器人粒子群算法

為了改善算法的性能，本文將第1部分中所提到的算法進行了有效的結合，在對上述算法改進策略分析的基礎上提出了一種具有動態自適應特性的機器人粒子群算法(DARPSO)。在DARPSO中，每個粒子的速度和位置更新公式如式(7)和式(8)所示：

(7)

(8)

對比第1部分提到的算法，所提出的算法有2個優點，分別是考慮了在真實環境中的障礙躲避和增強了算法跳出局部極小的能力。其中慣性權重的取值與所提到的“進化速度因素”和“聚集度因素”2個因素有關。這種改進在飛行器沖突解脫領域是前所未有的。這些改變，不僅使算法沒有陷入局部極值的情況，而且提高了粒子的搜索速度。這種方法非常迅速，因為在粒子工作的過程中都會對粒子群體每次迭代的狀態進行檢查。所提出的方法充分考慮了對粒子的限制，并針對粒子對目標進行搜索的問題提出了新的約束條件。許多學者也針對目標搜索問題介紹過一些約束[18]，本文中采用的約束條件為“粒子更新速度必須小于最大更新速度”和“考慮躲避障礙函數的計算”，這些約束條件能夠幫助粒子完成指定的動作。本文在考慮躲避真實環境障礙的基礎上，通過定義最大速度來解決早期的約束。事實上，這個最大值也用來作為公式(7)的最大邊界。由于DARPSO在更新粒子位置時只需要進行簡單的計算，所以上述2個約束條件也得到了解決。此外，在定義最大迭代次數上限的同時考慮了真實環境中飛行器的能源限制。

2.1 進化速度和聚集度

粒子的進化速度定義如式(9)所示：

(9)

全部粒子的聚集度定義如式(10)所示：

(10)

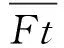
2.2 動態慣性權重的迭代策略

在粒子群算法的搜索過程中，粒子的進化速度和聚集度是2個特有的參數。所以，本文中慣性權重必須跟隨進化速度和聚集度的變化而變化，計算公式如式(11)所示：

(11)

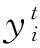
如果粒子尋找最優值的速度較慢，為了保證粒子更新速度，則需要減少粒子的數量。也就是說，如果粒子的位置彼此靠近，那么聚集度值就會變大。通過減小進化速度或者增大聚集度值就會增大慣性權重的影響并且削弱粒子當前最優和全局最優的跟蹤能力。簡而言之，這些影響因素保持了粒子之間的多樣性，是完成搜尋任務的重要保障。

(12)

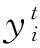
文獻[20]表示，在智能搜尋的過程中，將參數設置為c2>c1，這表示粒子在搜索目標任務中，社會認知部分成為主要內容。一般來說，c2的值越大收斂速度就越快。然而，相對于c1來說，非常大的c2會導致陷入局部極值的概率變大。出于此因，提出了一種新的方法定義c2的值，定義如式(13)所示：

c2=min((NR×ρ+c1),2c1)。

(13)

式中NR是粒子數量，同時ρ=0.4。在考慮粒子數量和初值的情況下研究了c2的計算公式，將式(13)引入到DARPSO中，在后續內容中經過一些不同環境中的實驗，可知此計算方法更簡單并且擁有較高的效率。當式(13)取最小值時，粒子數量的增長可以有效地控制參數c2的變化。一般的，c1=2，理想情況是在每次迭代過后c1的值稍微增大而c2的值稍微減小。感應系數c3定義如式(14)所示：

c3=2s(c1+c2)。

(14)

式中s是傳感器的數量。如果粒子和障礙物的距離很遠，粒子檢測不到障礙物，則s=0，c3=0。如果粒子和障礙物之間的距離縮短的話，那么c3的值就會增大，所以粒子會更多的考慮障礙物的因素并且盡可能與之保持距離。總之，DARPSO能夠保持粒子和目標搜索約束之間的多樣性，并保證計算簡單容易實現。

3 沖突解脫及仿真

3.1 算法有效性的驗證

一般來說，飛行器在同高度飛行時發生沖突，解脫方法一般有以下3種策略：1)調整航向的大小；2)改變航行速度；3)變化飛行高度。文獻[21]提出了一種沖突探測的幾何結構，并且給出了飛行沖突探測的邊界條件，以及在發生沖突時的航向角所需的調整量。本文將采用調整航向角的方法來對飛行器沖突進行解脫。

為了證明所提出算法的有效性，以下對比了改進的PSO和經典PSO在不同情況下的收斂速度，最優解以及收斂成功率。適應度函數選取2個基準測試函數，測試函數的參數設置如表1所示，測試結果如表2所示，其中穩定代數表示20次試驗達到最優時得到的迭代次數的平均值。2個基準測試函數分別是Sphere函數和Griewank函數。

Sphere函數：

Griewank函數：

由表1和表2中的數據可以看出，所提出的算法在跳出局部最優方面的能力有所增強，收斂精度和速度也有了顯著的提升。對比經典PSO，所提出的方法在搜索成功率和解決質量上更加突出。

表1 測試函數的參數設置

表2 測試函數的測試結果

3.2 沖突解脫仿真模擬

飛行沖突解脫問題的目標是，避免沖突時生成的新航跡同原航跡偏差最小，從而實現航跡最短，燃耗最小。本文所采用的沖突解脫目標函數為

式中dik和djk為飛機i和j在第k次迭代的位置與原航跡點的距離。為了飛行安全，必須時刻保持同一沖突區內的任意2架飛機間的距離大于最小安全間隔R，所以沖突解脫問題還需要滿足的約束條件為dij>R,其中R的取值[22]一般為20 km。

以2架飛機在同高度的障礙區域的沖突解脫問題進行仿真驗證。首先構建一個30 km×30 km的沖突避障區域，并設置2架飛機的起點和終點，如圖1所示。其中小方框代表2架飛行器的起點，五角星代表終點，小圓圈表示障礙點。在障礙點處生成高度為1 km的山峰，三維地形圖如圖2所示。如果2架飛行器以相同的速度飛往目標地點，那么在區域的中心點會發生相撞，如圖3所示。圖4是2架飛行器發生沖突時DARPSO生成的解脫航跡，從圖中可以看出，所提出的改進粒子群算法能夠完成對沖突的解脫，并且能夠使解脫后的航跡平滑，與原航跡偏差較小。

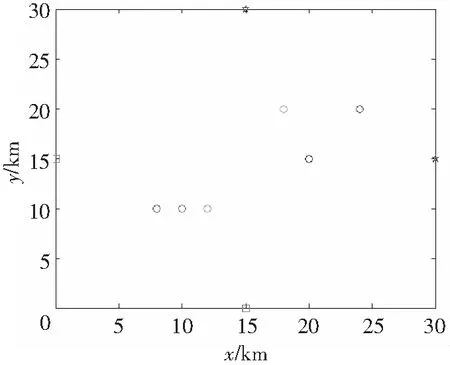
圖1 初始化飛行器起始點、障礙物坐標Fig.1 Initial positions of aircraft goals and obstacles

圖2 障礙的三維地形圖Fig.2 Three-dimensional terrain of the obstacles

圖3 2架飛行器沖突示意圖Fig.3 Conflict schematic view of two aircrafts

圖4 飛行器沖突解脫航跡Fig.4 Aircrafts conflict resolution trajectory

4 結 語

本文針對飛行器沖突解脫問題，在PSO的基礎上提出一種新的解脫算法DARPSO，建立了適合解決問題的粒子更新表達式。DARPSO考慮了真實環境中障礙的影響，保證了粒子在搜索過程中的多樣性，仿真結果顯示DARPSO跳出局部極小的能力和收斂速度有了顯著提升。該算法作為一種通用的優化算法，也可以應用到機器人路徑規劃、無人機航跡規劃等問題中，具有廣泛的應用價值。本文不足之處在于只考慮了二維空域下的解脫策略，由于飛行器數量的增加以及不確定環境中的其他影響因素的存在，有待于將飛行器沖突解脫問題拓展到三維空域中進行更加深入的研究。

[1] 王利亞.提高空域使用效率確保飛行安全順暢[J].空中交通管理，2011(6)：4-6.

WANG Liya. Improving efficiency in use of airspace to ensure flight safety and smoothness[J]. Air Traffic Management, 2011 (6):4-6.

[2] 崔德光,程朋,耿睿. 空中交通管制自動化中的沖突概率分析[J].清華大學學報(自然科學版), 2000, 40(11)：119-122.

CUI Deguang, CHENG Peng, GENG Rui. Probability analysis of collision in Automation Air Traffic Control[J]. Journal of Tsinghua University(Science and Technology),2000, 40(11):119-122.

[3] 王世錦，隋東．低空空域飛行沖突風險研究[J]．西南交通大學學報,2010, 45(1)：116-123.

WANG Shijing, SUI Dong. Risk analysis of conflict in low altitude airspace[J]. Journal of Southwest Jiaotong University, 2010, 45(1):116-123.

[4] MARINI F, WALCZAK B. Particle swarm optimization(PSO)：A tutorial[J]. Chemometrics and Intelligent Laboratory Systems, 2015, 49(1):153-165.

[5] 張萬緒，張向蘭，李瑩．基于改進粒子群算法的智能機器人路徑規劃[J]．計算機應用，2014, 34(2)：510-513.

ZHANG Wanxu, ZHANG Xianglan, LI Ying. Path planning for intelligent robots based on improved particle swarm optimization algorithm[J]. Journal of Computer Applications, 2014, 34(2):510-513.

[6] 甄然，王開拓，吳學禮．基于數字地圖預處理的飛行器航及規劃[J]．河北科技大學學報，2015, 36(2)：195-202.

ZHEN Ran, WANG Kaituo, WU Xueli. Aircraft route planning based on digital map pre-treatment[J]. Journal of Hebei University of Science and Technology, 2015, 36(2): 195-202．

[7] 任子暉，王堅.加速收斂的粒子群優化算法[J].控制與決策，2011,26(2)：201-206.

REN Zihui, WANG Jian. Accelerate convergence particle swarm optimization algorithm[J]. Control and Decision, 2011, 26(2):201-206.

[8] KENNEDY M, EBERHART B. Particle swarm optimization[J]. Proceedings of the Conference on Neural Networks, 1995 (8):1942-1948.

[9] KLOSE C. Algorithms for solving the single-sink fixed-charge transportation problem[J]. Computers and Operations Research, 2006, 35(6):2079-2092.

[10] 呂振肅，侯志榮.自適應變異的粒子群優化算法[J] .電子學報，2004, 32(3)：416-420.

LYU Zhensu, HOU Zhirong. Particle swarm optimization with adaptive mutation[J]. Acta Electronica Sinica, 2004, 32(3):416-420.

[11] CHYAN G, PONNAM S. Obstacle avoidance control of redundant robots using variants of particle swarm optimization[J]. Robot Comput Integr Manuf, 2012, 28(2):147-153.

[12] DADGAR M, JAFARI S ,ALI H. A PSO-based multi-robot cooperation method for target searching in unknown environments[J]. Neurocomputing, 2015, 11(7):1-13.

[13] SENTHILKUMAR K. Multi-robot exploration and terrain coverage in an unknown environment[J]. Robotics and Autonomous Systems, 2012, 60(1):123-132.

[14] SCHILLING K, JUNGIUS C. Mobile robots for planetary exploration[J]. Control Engineering Practice, 1996, 4(4):513-524.

[15] ZHANG Jianhua, GONG Dunwei, ZHANG Yong. A niching PSO-based multi-robot cooperation method for localizing odor sources[J]. Neurocomputing, 2014, 123(10):308-317.

[16] YANG Xueming, YUAN Jinsha, MAO Huina. A modified particle swarm optimizer with dynamic adaptation[J]. Applied Mathematics and Computation, 2007, 189(12):1205-1213.

[17] ALFI A. PSO with adaptive mutation and inertia weight and its application in parameter estimation of dynamic systems[J]. Acta Automatica Sinica, 2011, 37(5):541-549.

[18] MATSUNO Y, TSUCHIYA T, WEI Jian, et al. Stochastic optimal control for aircraft conflict resolution under wind uncertainty[J]. Aerospace Science and Technology, 2015, 43(2):77-88.

[19] CAI Yifan. An improved PSO-based approach with dynamic parameter tuning for cooperative multi-robot target searching in complex unknown environments[J]. International Journal of Control, 2013, 86(10):1720-1732.

[20] ZHANG Yong, GONG Dunwei , ZHANG Jianhua. Robot path planning in uncertain environment using multi-objective particle swarm optimization[J]. Neurocomputing, 2013, 103(1):172-185.

[21] ANTONIO A, LAUREANO F. Multiobjective optimization for aircraft conflict resolution： A metaheuristic approach[J]. European Journal of Operational Research, 2016, 248(5):691-702.

[22] MARIA P, HU Jianghai, JOHN L, et al. A probabilistic approach to aircraft conflict detection[J]. IEEE Transactions on Intelligent Transportation Systems, 2000, 1(4):199-220.

Study of the aircraft conflict resolution method based on modified particle swarm optimization

ZHEN Ran1,2, SI Chao1,2, WU Xueli1,2, ZHANG Jianhua1,2, WU Xiaojing1,2

(1.School of Electrical Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China; 2. Hebei Provincial Research Center for Technologies in Process Engineering Automation, Shijiazhuang, Hebei 050018, China)

Conflict resolution requires the aircraft to adopt an effective method to meet the constraints of the working space. Aiming at the problem of conflict resolution in multi obstacle environment, a novelty algorithm based on particle swarm optimization (PSO) is proposed for conflict resolution which meets the mentioned constrains. The proposed DARPSO is similar to PSO with two modifications: firstly, it takes into account the obstacle avoidance; secondly, it has a mechanism to escape from local optima. Various experimental results obtained in simulations show that the proposed DARPSO is much more superior than PSO. The DARPSO is applied to the process of conflict resolution of aircrafts, and it is simulated. The simulation results show that the proposed algorithm can avoid the obstacles and complete conflict resolution effectively.

algorithm theories; aircraft; conflict detection; conflict resolution; particle swarm optimization

1008-1542(2016)05-0491-06

10.7535/hbkd.2016yx05010

2016-05-24；

2016-09-09；責任編輯：李 穆

河北省自然科學基金(F2015208128，F2014208119)；河北省教育廳青年基金(QN20140157，BJ2016020)

甄 然(1971—)，女，河北安國人，副教授，主要從事控制科學與控制工程方面的研究。

E-mail:zhenranzr@126.com

TP273; V19

A

甄 然，司 超，吳學禮,等.基于改進粒子群算法的飛行器沖突解脫方法研究[J].河北科技大學學報,2016,37(5):491-496.

ZHEN Ran, SI Chao,WU Xueli,et.al.Study of the aircraft conflict resolution method based on modified particle swarm optimization[J].Journal of Hebei University of Science and Technology,2016,37(5):491-496.