擴散器角度對流體流動能量損失的研究*

曹嘉佳

(蘇州工業園區職業技術學院機電工程系，江蘇蘇州215123)

?

擴散器角度對流體流動能量損失的研究*

曹嘉佳

(蘇州工業園區職業技術學院機電工程系，江蘇蘇州215123)

空氣動力特征, 例如空氣分流現象，壓力和阻力，都對賽車行駛過程中的燃料消耗的經濟性和運行的平穩性有著重要影響。 本文主要針對擴散器的錐角大小進行研究。通過改變擴散器角度的大小調節汽車行駛時車身遇到的阻力以及能量的損失，采用實驗和CFD(Computational Fluid Dynamic)數值模擬兩種方式對三個不同角度(5°，24°，60°)的擴散器進行研究。通過比較實驗與模擬結果顯示，PRC壓力恢復系數隨著擴散器角度的減小而增大。當角度在5°時，空氣在擴散器內能量損失最少，這時擴散器發揮最佳性能。

擴散器 錐角 能量損失 數值模擬

擴散器作為一種重要的裝置被用于各行各業[1]。在F1方程式賽車上[2-3]，F1方程式賽車車尾的擴散器，賽車在高速彎道行駛時，通過使用擴散器來避免空氣的分流現象并且減小空氣流通的阻力和空氣的升力，從而降低流通中的能量損失來控制賽車行駛過程中的平穩性和燃料燃燒的經濟性[4-7]。2011年吉林大學通過計算機流體數值模擬的方法對5個不同角度的擴散器(0°，3°，6°，9.8°，12°)進行研究，實驗結果證明空氣的阻力特征隨著擴散器角度的減小先增加后減小[8]。2014年印度的維斯瓦力亞大學通過CFD方法分析研究(7°，8°，9°，10°)四個不同角度的擴散器，結果與吉林大學的實驗結果相同，但他們得出在7°時，流體沒有分流現象，所以此時能量損失最少[9]。所以他們認為擴散器角度在7°以下的角度能發揮擴散器的最大效率。之前的實驗都驗證了隨著擴散器角度的減少，空氣阻力和升力越小，從而使汽車具有更優的平穩性，但是7°以下這個范圍還是很廣，擴散器角度的選擇性很多，始終沒有確定最優的擴散器角度值。本次研究是對三個不同角度的擴散器(5°，24°，60°)來進一步驗證之前的結果，并且更加精確的找出能達到擴散器最優效果的錐角讀數。

1 實驗說明及步驟

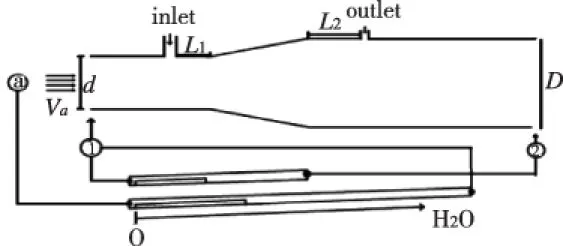
圖1 錐形擴散器平面圖

由圖1可以得出，這個擴散器由三部分組成：進氣管，中部錐形管，出氣管。d是擴散器進口直徑；D是擴散器出口直徑；Va是自由流體的速度；在擴散器下方有兩個壓力計，短的一根壓力計是用來測試進口①與出口②之間的壓力(P2)，長壓力管是用來測試外界大氣Pa和進氣口①間壓力(P1)。

實驗步驟：1)選擇三個不同角度的擴散器：5°，24°，60°。2)測量并記錄下進口管上的監測點到中部錐形管的距離。3)檢測設備上水泡的位置，為了確保實驗準確性，調節兩個旋鈕使水泡移動到容器中部。4)打開進氣開關調到最大速度。5)等待一分鐘，直到壓力表中流體趨于穩定，記錄下兩個壓力數值(由于度數誤差，記錄下來的數據需要加上或減去0.1。6)然后再把進口速度調到中速和低速，分別記錄下壓力計度數。

2 實驗計算

2.1 計算進口流體速度

通過伯努利方程(1)計算出擴散器進口的速度，此時壓力損失可忽略不計。Pa指的是大氣的壓強；V1是擴散器進口速度。當Va?V1，Va可以被忽略，此時伯努利方程可以被簡化為式(2)。

(1)

(2)

2.2 雷諾數(Reynolds Number)

雷諾數是用來判斷流體特性的一個重要依據。當Re≥2 000，此時流體可認為是湍流，反之則為層流。根據雷諾數(Reynolds Number)的定義很容易得到它的計算公式如公式(3)。ρ是流體的密度；μ流體的粘度。

(3)

2.3 能量損失

根據簡化后的伯努利方程(4)和雷諾數方程可得到PRC計算方程如式(6)：

(4)

(5)

能量損失=PRC(ideal)-PRC

(6)

3 實驗結果

在整個實驗中，選取了三個不同角度的擴散器(5°，24°，60°)來測試空氣流過擴散器的流體參數變化。表1收集了實驗結果數據。同一個錐角擴散器，通過控制進口流體的速度大小來監測記錄下壓力的變化，根據計算所得壓力差來計算出壓力恢復系數(PRC)值。根據所得實驗數據得出擴散器錐角和雷諾數對流體運動中能量損失的關系(圖2)。

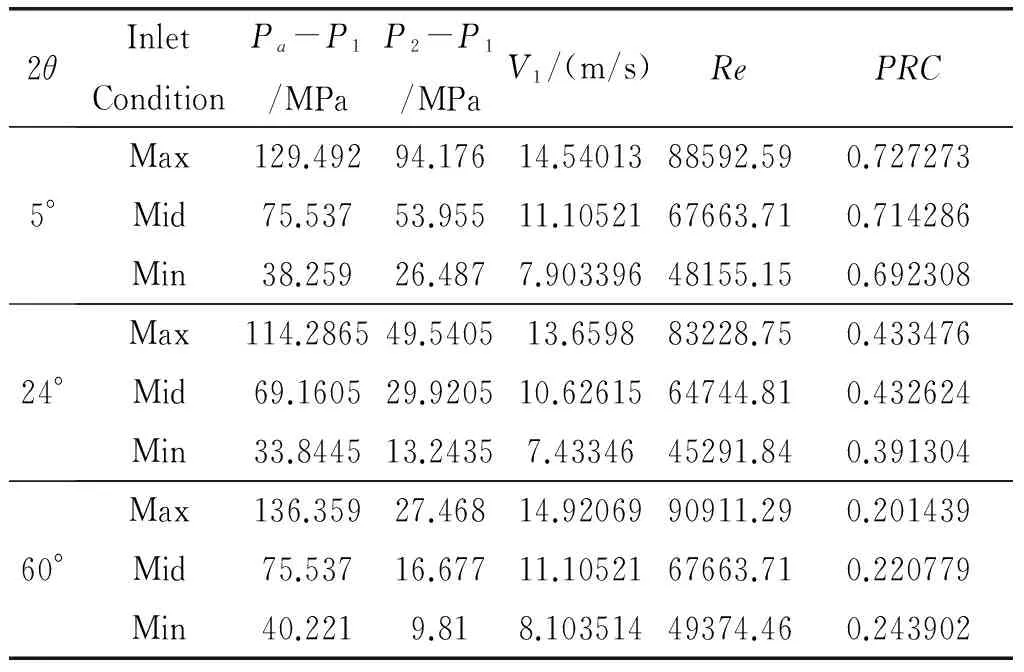
表1 實驗結果

4 CFD數值模擬

4.1 建模和網格生產

實驗所用的設備如圖1所示，錐形擴散器是一個對稱的結構，為了減少模擬時間，并且簡化實際問題，可以將三維的模型轉化為二維的模型進行模準確率的結果，劃分后的網格必須進行優化調試以得到最適合模擬流體運動的網格。最后將優化后的網格導入FLUENT，進行模擬計算流體通過擴散器中的物理量變化。圖3呈現了完整的5°擴散器建模。圖4為生成后的網格結構。

4.2 流體特性假設

研究流體運動時，雷諾數是一個用來判定流體流動特征的參數。當Re<2 000，流體屬于層流。Re≥2 000，此時流體可被認為是湍流。根據公式(5)計算得到此次在擴散器中流動的流體屬性為湍流。在這個特殊的研究案例中為了減少計算時間，選用ReynoldsAveragedNavierStokesEquation(RANS)來解決湍流問題。當考慮到模擬湍流的準確性和計算的經濟性，選擇標準k-ε模型。為了簡化模擬的復雜性，選擇運用standardwallfunction。由于它不需要太高精度的網格質量，被廣泛的應用于工業流體研究中。并且在Fluent模擬中選用簡化后的納維-斯托克斯方程k-ε方程作為求解方法。k表示湍流的勢能，ε表示流體流動時的能量損失[11]。選擇這個k-ε模型求解法也保證了適當的計算時間和計算結果的準確性。

4.3 模擬結果與分析討論

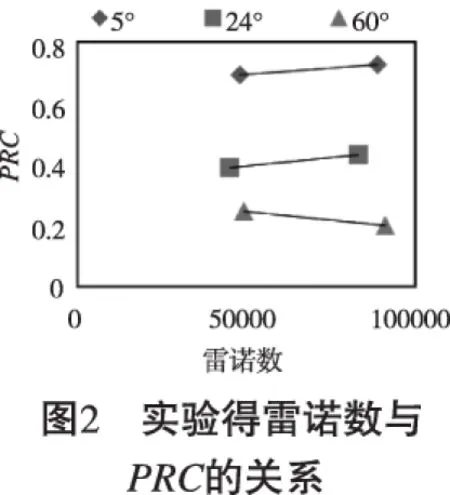
圖2展示了流體在不同狀態時的能量損失情況。由圖2可知，三個不同角度擴散器實驗結果都顯示隨著雷諾數的增長，恢復參數(PRC)數值幾乎趨于平穩。雖然60°擴散器實驗數據顯示PRC值有微小的下降，由于讀數時觀察視角不同，造成的讀數誤差，所以這個微小變化可以被忽略。 圖3顯示了PRC與擴散器角度的關系。很明顯，隨著錐角的增加，相對應PRC數值減小，流體流動過程中能量損失越大。

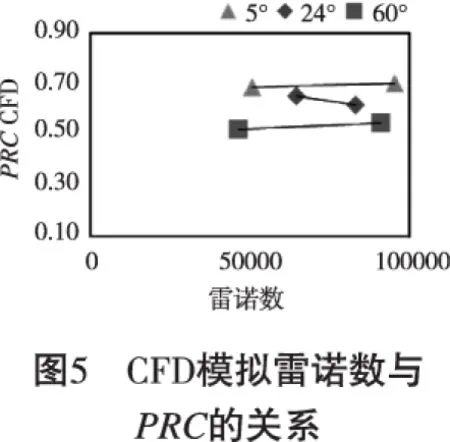
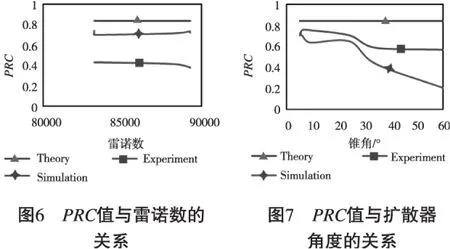
通過CFD模擬實驗，得到PRC與雷諾數和擴散器錐角的關系如圖5。 從圖6可以得出，隨著雷諾數的增長，PRC值幾乎恒定不變。但是，擴散器錐角變化對PRC值的影響很大，隨著擴散器錐角增大，PRC的值也隨之增長。這個結論與實驗得出結論一致。從實驗和模擬結果來看，雷諾數對PRC值的影響微不足道。但是，擴散器的角度對PRC的值有著重要的影響。由圖5得出，隨著擴壓器角度的增加，PRC值將減少。當流體通過60°的傾斜邊時，流體流動分離導致一部分的動能損失，此時的PRC值最小。這意味著，隨著錐角角度的增加，更多的能量可能會丟失。當角度為5°時，此時流體能量損失最少，并且此時實驗與模擬值最為接近。由圖6和7可得，實驗的結果與CFD仿真結果一致且相對接近，證明CFD數值模擬的正確性。

5 結論

通過比較實驗和模擬結果，擴散器中流體流動的能量損失與擴散器的角度有關，角度越小，能量損失越小，尤其是在5°的時候，流體基本可以避免分流現象，能量損失達到最小，此時擴散器達到最優使用效率。并且，通過比較實驗和數值模擬兩種方式，CFD數值模擬更加省時，且結果的準確性很高。因此，在解決有關流體研究方面問題時，CFD模擬方法是一種可靠的首選方式。同時，本次模擬只模擬了2D模型，未來需對3D模型進行進一步的研究。

[1]RuhrmannA,ZhangX.Influenceofdiffuserangleonabluffbodyingroundeffect[J].JournalofFluidsEngineering, 2003,125(2): 332-338.

[2]AhmedH,ChackoS.Computationaloptimizationofvehicleaerodynamics[C]//Proceedingsofthe23rdInternationalDAAAMSymposium.Vienna:DAAAMInternational,2012: 0313-0318.

[3] Singh J, Randhawa J S. CFD analysis of aerodynamic drag reduction of automobile car-a review[J]. International Journal of Science and Research, 2014,3(6):213-215.

[4] TienPhuc D, ZhengQi G, Zhen C. Numerical simulation of the flow field around generic formula one[J]. Journal of Applied Fluid Mechanics, 2016,9(1):443-450.

[5] Lefebvre A H, Ballal D R. Gas Turbine combustion:Alternative fuels and emissions[M].3rd ed. CRC Press, 2010: 79-112.

[6] Chandra S, Lee A, Gorrell S, et al. CFD analysis of PACE formula-1 Car[J]. Computer-Aided Design and Applications,2011(1): 1-14.

[7] Chandavari V, Palekar S. Diffuser angle control to avoid flow separation[J]. International Journal of Technical Research and Applications, 2014,2(5):16-21.

[8] Hu X J, Zhang R, Ye J, et al. Influence of different diffuser angle on sedan’s aerodynamic characteristics[J]. Physics Procedia,2011, 22: 239-245.

[9] Anderson J. Computational fluid dynamics[M]. New York: McGraw-Hill,1995.

[10] Sagar D, Paul A R, Jain A. Computational fluid dynamics investigation of turbulent separated flows in axisymmetric diffusers[J]. International Journal of Engineering, Science and Technology, 2011,3(2):104-109.

[11] Versteeg H, Malalasekera W. An introduction to computational fluid dynamics[M]. Harlow: Longman, 1996.

The influence of diffuser angle on the fluid energy loss

CAO Jiajia

The aerodynamic characteristics, such as split-flow, pressure and drag, would significantly influence the fuel consumption and stability of the racing car. In this study, we analyzed the influence of the diffuser angle on the drag and the energy loss of the car through experiment and CFD numerical simulation of three diffusers with different angles(5°，24°，60°). The results showed that, the pressure recovery coefficient(PRC) increased with the decrease of the diffuser angle. When the angle was 5°, the energy loss in the diffuser was the lowest, and the diffuser displayed the best performance.

diffuser，angle，energy loss，numerical simulation

TK41

A

1002-6886(2016)05-0071-04

“江蘇高校品牌專業建設工程資助項目”，項目編號：PPZY2015A088。

曹嘉佳 (1992-)，女，碩士研究生，教師，主要研究流體力學工程。

2016-04-29