數據的集中趨勢與離散程度“疑難雜癥”會診

陸櫻花

數據的集中趨勢與離散程度“疑難雜癥”會診

陸櫻花

同學們在學習《數據的集中趨勢與離散程度》這一章節時，會遇到一些共性的問題，現在我們將相關的典型錯題做如下整理，希望能對同學們有所幫助.

一、認清本質，算對平均數

例1（2015·廣西玉林）學校抽查了30名學生參加“學雷鋒社會實踐”活動的次數，并根據數據繪制成了條形統計圖，則30名學生參加活動的平均次數是_________.

【診斷分析】30名同學參加社會實踐活動次數的平均數不僅與個人社會實踐活動次數有關，還與不同活動次數所對應的人員數量有關.

【正確解答】

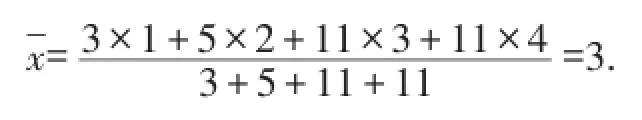
二、應對中位數，排序是關鍵，奇偶有區別

例2學校團委組織“陽光助殘”捐款活動，九（1）班學生捐款情況如下表：

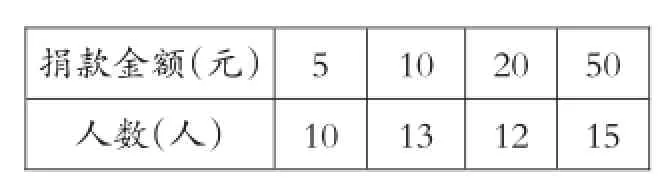
捐款金額（元）人數（人）5 1 0 1 0 1 3 2 0 1 2 5 0 1 5

則學生捐款金額的中位數是__________.

【錯誤解答】將捐款金額5，10，20，50排序，所以取10和20的平均數15（元）；將捐款人數10，12，13，15排序，故12.5（人）.

【診斷分析】對于這種求表格中數據中位數的題目，首先要看清研究對象，此處要求研究捐款金額的中位數，則確定要分析的是以元為單位的那組數據.

【正確解答】若從小到大排列，則為10個5，13個10，12個20，15個50，共有50個數，則中位數為第25、26個數的平均數，第25、26個數均為20，所以中位數是20.

三、多則為“眾”，眾數必存在于原數據中

（1）眾數是出現次數最多的數據，而非出現的次數.

例3某鞋店銷售了9雙鞋，各種尺碼的銷售量如下表：

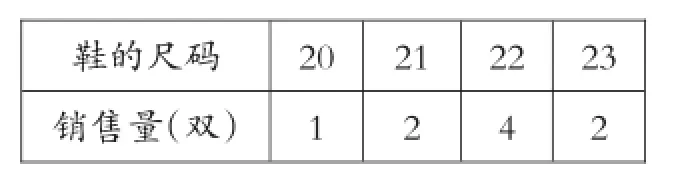
鞋的尺碼銷售量（雙）20 1 21 2 22 4 23 2

計算這9雙鞋尺碼的眾數.

【錯誤解答】22出現了4次，所以眾數為4.

【診斷分析】本題研究對象是鞋的尺碼，所以眾數應圍繞鞋的尺碼求解.在理解上要明確出現次數最多的那個數據，而不是出現的次數.

【正確解答】這9個數據中出現次數最多的數據是22，所以眾數是22.

（2）一組數據可以同時有多個眾數.

例410名工人，某天生產同一零件，生產的件數是：15，17，14，10，15，19，17，16，14，12，則這一組數據的眾數是_________.

【錯誤解答】15.

【診斷分析】一組數據的眾數可能不止一個.求一組數據的眾數的方法：找出頻數最多的那個數據，若幾個數據頻數都是最多且相同，此時眾數就是這多個數據.若每個數據都只出現一次，則這組數據沒有眾數.

【正確解答】題中14、15、17都出現2次，所以這組數據的眾數是14、15和17.

四、極差考慮要全面，不確定時要分類

例5已知一組數據：-1，4，6，x的極差為9，則x的值為__________.

【錯誤解答】8.

【診斷分析】一組數據中最大值與最小值的差叫做這組數據的極差，即極差=最大值-最小值.本題中，確定的三個數據-1＜4＜6，6-（-1）=7＜9，所以x必為最大值或最小值.當x為最小值時，6為最大值；當x為最大值，則-1為最小值.

【正確解答】x-（-1）=9，x的值為8；6-x=9，x的值為-3.所以x的值為8或-3.

五、方差公式要熟練，重要結論要記牢

（1）連續五個整數的方差均為2.

例6（2015·內蒙古包頭）一組數據5，2，x，6，4的平均數是4，這組數據的方差是________.

【錯誤解答】10.

【診斷分析】方差是反映一組數據的波動大小的一個量，通常用s2表示.計算時，經常要用到公式］.記錯公式及計算能力不過關是造成錯誤的主要原因.若能巧用“連續五個整數方差為2”這一結論，此處可起到事半功倍的效果.此結論說明如下：不妨設連續5個整數為a-2，a-1，a，a+1，a+2，則這五個數的平均數為a，代入公式得：s2=（4+1+4+1）=2.

【正確解答】2.

（2）①若一組數據x1，x2，…，xn的方差是s2，則數據x1+b，x2+b，…，xn+b的方差還是s2；

①若一組數據x1，x2，…，xn的方差是s2，則數據ax1，ax2，…，axn的方差是a2s2。

③若一組數據x1，x2，…，xn的方差是s2，則數據的ax1+b，ax2+b，…，axn+b的方差是a2s2.

例7（2015·貴州遵義）如果一組數據x1，x2，…xn的方差是4，那么另一組數據x1+3，x2+ 3，…，xn+3的方差是_______.

【錯誤解答】7.

【診斷分析】當一組數據同時加上或減去同一個數后，新數據的方差不變.

【正確解答】4.

本次“會診”到此就要結束了，相信同學們可以借助診斷結論，在“作戰”中靈活應用，享受不俗的作戰成果！

（作者單位：江蘇省常州市武進區湖塘實驗中學）