一類具群體防御狀態及Holling III型功能反應的捕食系統正周期解的全局吸引性

劉昌東，江 如，柴華金

（廣東海洋大學理學院，廣東 湛江 524088）

一類具群體防御狀態及Holling III型功能反應的捕食系統正周期解的全局吸引性

劉昌東，江 如，柴華金

（廣東海洋大學理學院，廣東 湛江 524088）

應用微分方程比較原理，重合度理論中的Mawhin's延拓定理和Lyapunov函數研究一類具有相互干擾和群體防御狀態及Holling III型功能反應的捕食系統正周期解的存在性和全局吸引性。推廣了有關文獻的研究和結果。

功能反應模型；正周期解；Lyapunov函數；全局吸引性；Mawhin延拓定理

在自然界眾多物種于同一生態環境中共存，它們之間必然相互影響，這是一種自然界的普遍現象.為描述和研究生物間的這種現象，數學生態學者建立了種類多樣的數學生態微分模型.1971年Hassell在觀察研究兩個物種的行為特征時，提出了一個同時考慮到密度制約，功能性反應和相互干擾時捕食者和被捕食者之間競爭的一般微分模型［1］

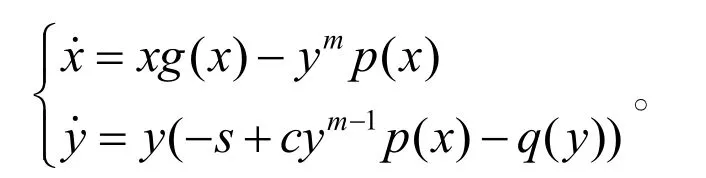
其中x（t），y（t）分別表示被捕食和捕食種群在時刻t的密度，g（x）是食餌種群在沒有捕食者存在時的增長率，m（0＜m＜1）為相互干擾常數，p（x）為捕食者的功能性反應函數（捕食者的捕食率）.近年來，這一模型的一些特殊的時變形式被廣泛研究，如文獻［2-7］。

朱和王［2］研究了一類互相干擾和具有Holling II型功能性反應模型

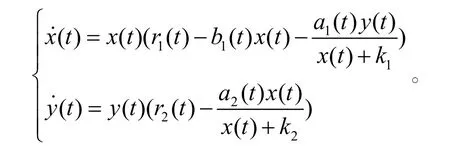
王和杜等［4］，呂和杜［5］研究了一類具有相互干擾和Holling III型功能性反應的Lotka-Volterra模型

并且都獲得上述兩類模型正周期解的存在性和全局吸引性的充分條件。

本文研究一類更一般的具有相互干擾和在群體防御狀態下的Holling III型功能性反應模型［8］

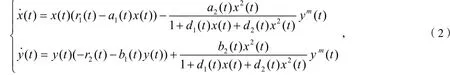
初始值

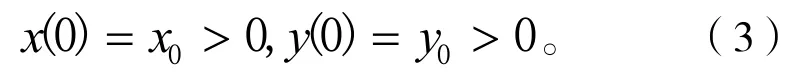
其中x（t），y（t）表示被捕食種群和捕食種群在時刻t的密度，ai（t），bi（t）和ri（t）（i=1，2）及 di（t）（i=1，2）均定義在［0，+∞）上的正-ω周期連續函數，0＜m＜1為干擾系數，其余詳細的生態意義見文獻［1-8］。本研究獲得該系統的解的最終有界性，正周期解的存在性和全局吸引性的充分條件，推廣了文獻［2，4-5］的研究。

為研究方便，我們引入下面記號：對于［0，+∞）上的連續函數f（t），記

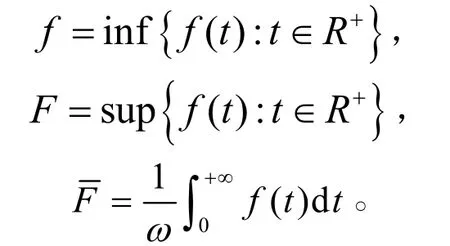
顯然系統式（2）包含了系統式（1）作為特例，故本研究推廣了文獻［4-5］的研究。

1 解的有界性

設f（t）在［0，+∞）上連續，則不難證明初值問題

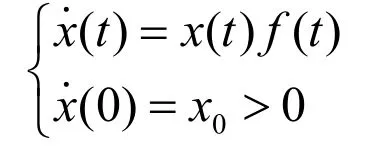
的解x（t）＞0在［0，+∞）上恒成立。

據此，對系統式（2）積分可知，系統式（2）滿足初值式（3）的解（x（t），y（t））T存在且均為正解，即當

引理1.1 設x（t）是初值問題

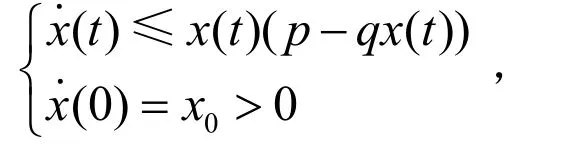
或

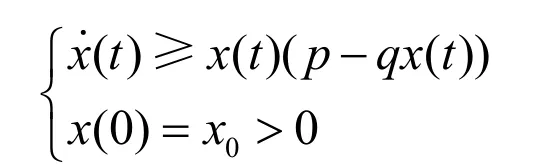
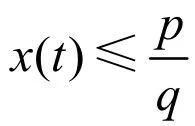
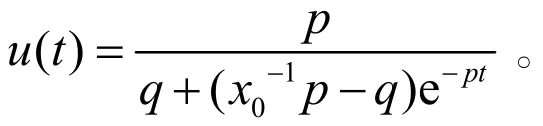
由比較原理得

或

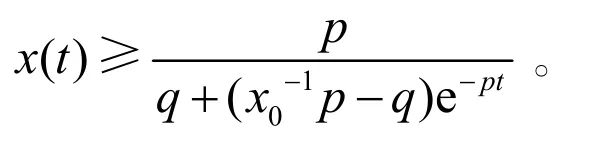
故存在T1＞0，當t＞T1時，

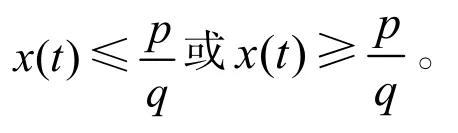
證畢。

引理1.2 設p＞0，q＞0為常數，x（t）是初值問題

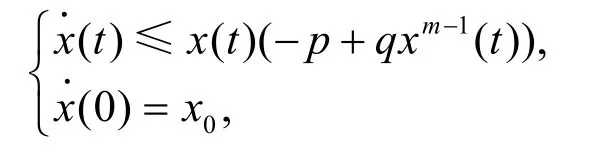
或

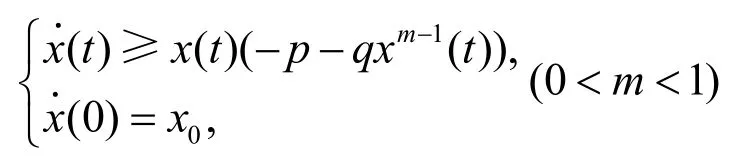
的解，則存在T2＞0，當t＞T2時，

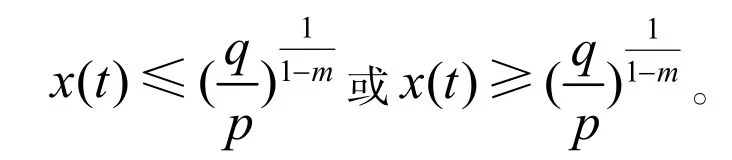
證明 用證明引理1.1的方法可得。

下面用引理1.1和引理1.2證明系統式（2）的解最終有界性。

定理1.1 設（x（t），y（t））T是系統式（2）滿足初值式（3）的解，則存在正常數Ki，Li（i=1，2）和T＞0，當t＞T時有

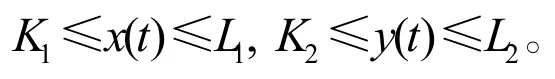
這里Li，Ki（i=1，2）在下面證明中給出。

證明 由式（2）的第1個方程得

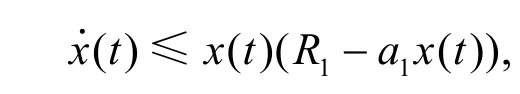
根據引理1.1，存在T1＞0，當t＞T1時

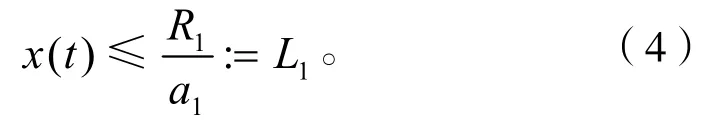
由式（2）的第2個方程得

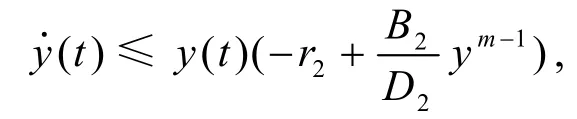
根據引理1.2，存在T2＞T1，當t＞T2時

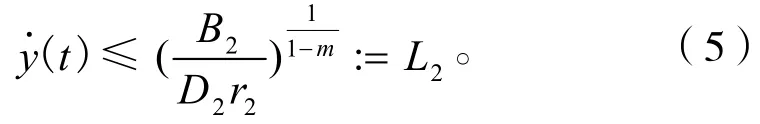
再由式（2）第1個方程得

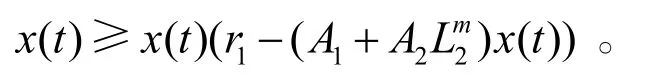
根據引理1.1，存在T3＞T2，當t＞T3時

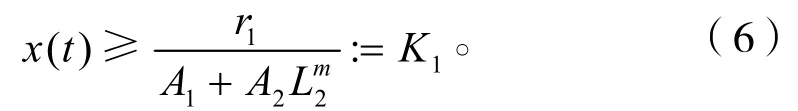
接著由式（2）的第2個方程得

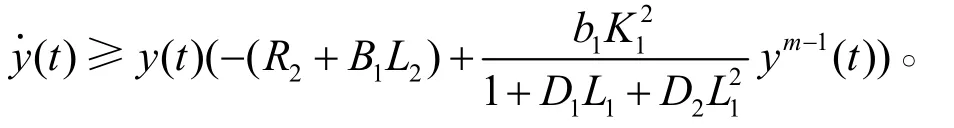
根據引理1.2，存在T4＞T3，當t＞T4時，有

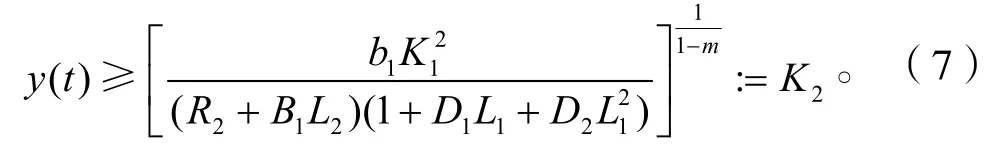
綜合式（4），（5），（6）和式（7）知，存在T＞T4，當t＞T時，有

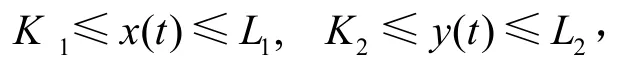
而且Ki，Li（i=1，2）均與系統式（2）的任何解無關，僅由系統的系數決定。證畢。

2 周期解的存在性

先引入Mawhin延拓定理。

定義2.1［9］設X和Y是兩個Banach空間，

是一個線性映射，如果滿足條件：（i）ImL是Y的閉子空間；，則稱L是指標為零的Fredholm算子。

設L是指標為零的Fredholm算子，則存在線性投影算子

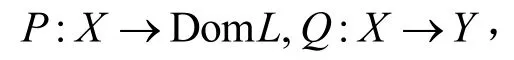
滿足

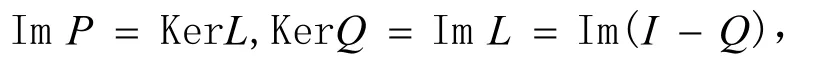
并且

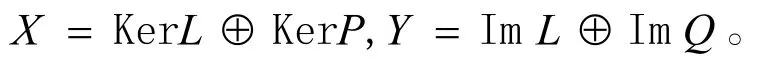
映射

是可逆映射，其逆記為KP，則

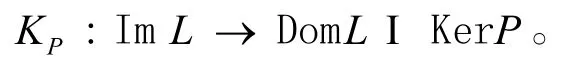
定義2.2［9］設

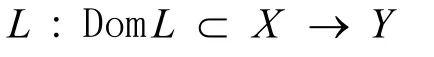
是指標為零的Fredholm算子，Ω?X是任一開集，N：X →Y是一個連續映射。如果QN（）在Y中是有界的，而且是X的相對緊集，則稱N在Ω上是L—緊的。

引理2.1［9］設X和Y都是Banach空間，是一個零指標的Fredholm算子，Ω?X是一個有界開集，上是L—緊的。如果下面條件都滿足：

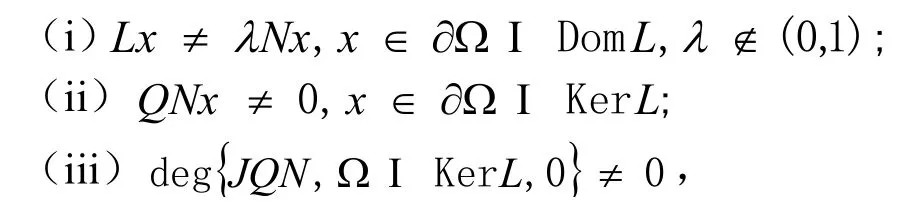
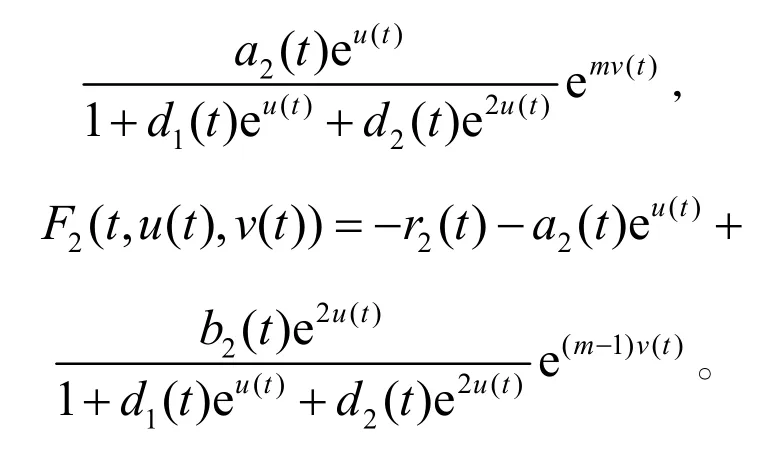
考慮系統

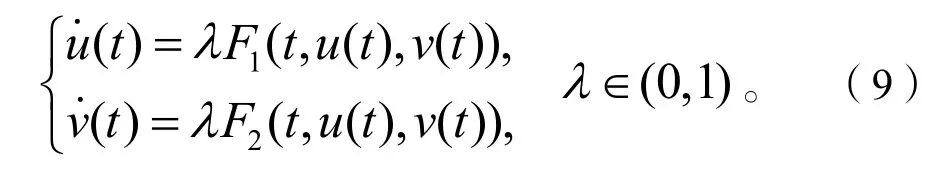
設

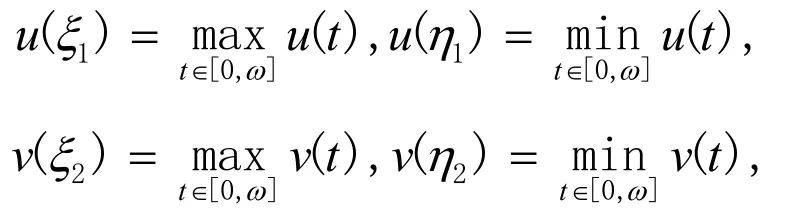
則

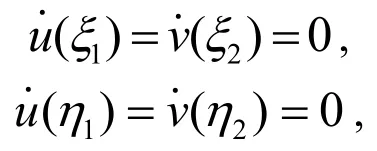
代入式（8）得

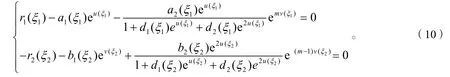
由式（10）第1式得

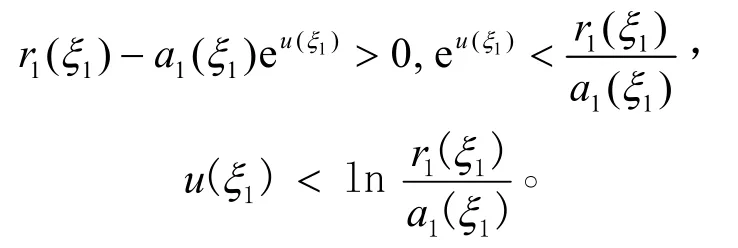
所以

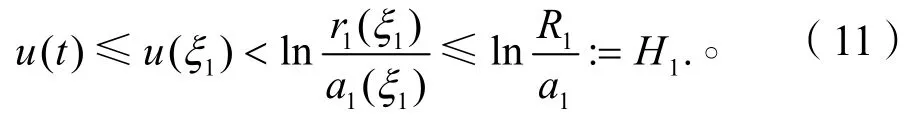
由式（10）的第2式得

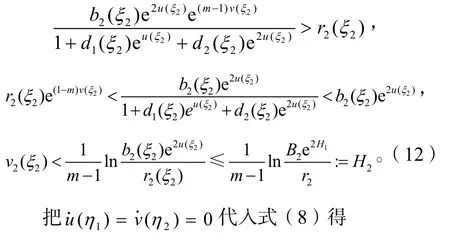
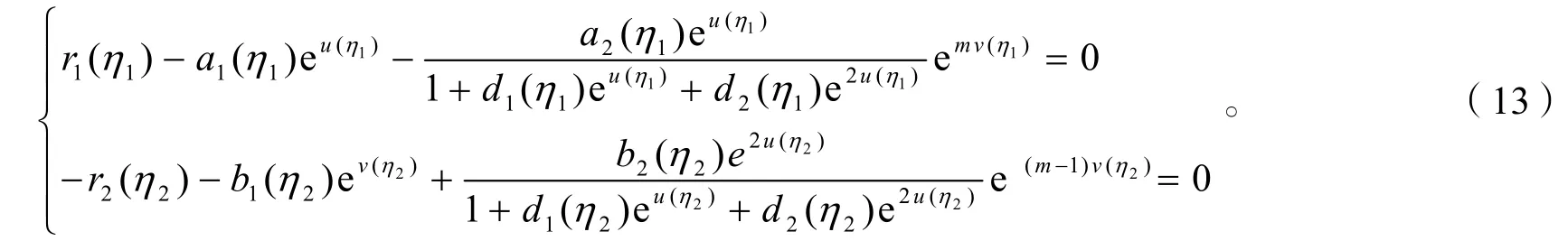
由式（13）的第1式得

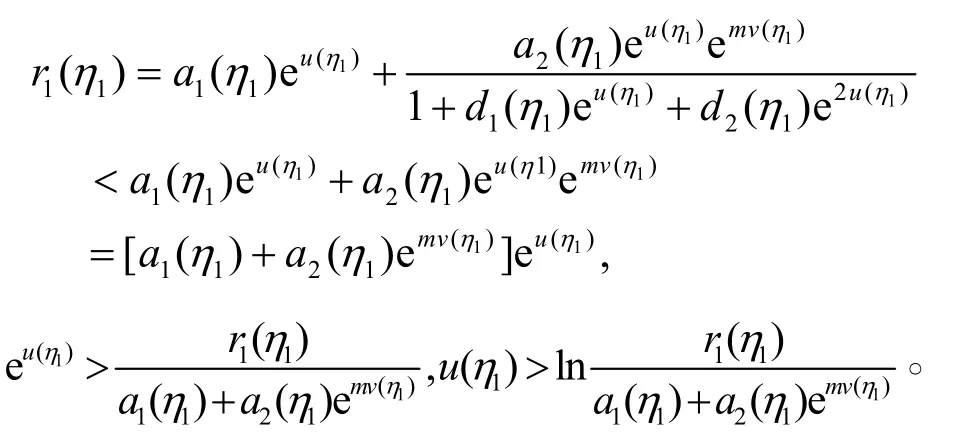
于是有

又由式（13）的第2式得

于是有

綜合式（11），（12），（14）和式（15）可知，對任何t∈［0，］ω，都有

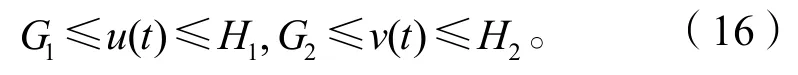
取

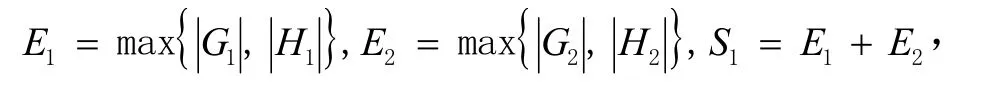
則有

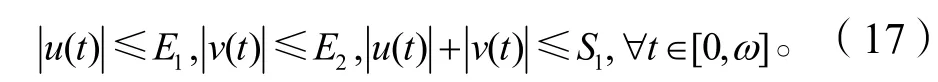
證畢。

如果（u，v）T是系統式（9）的一個常向量解，則有

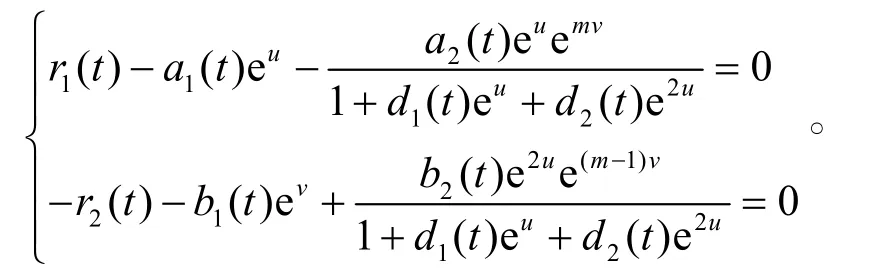
對上面兩式分別在［0，］ω上積分，并根據第二積分中值定理得

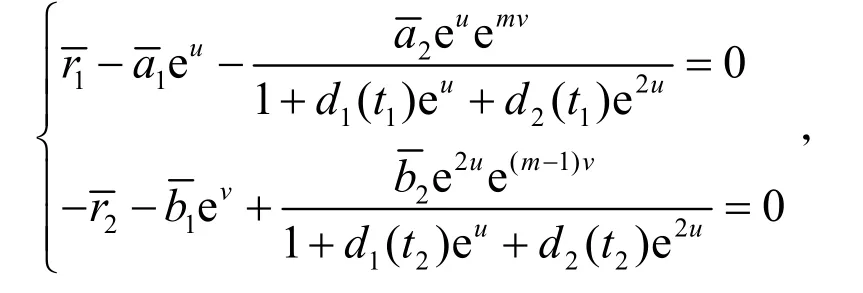
考慮代數方程組

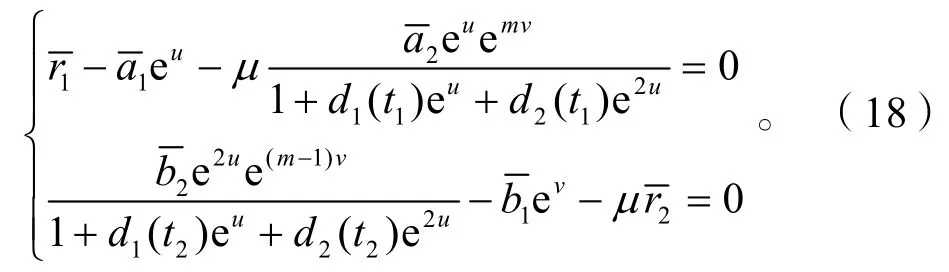
其中μ∈［0，1］是一個參數。有下面引理。

證明 由式（18）第1式得

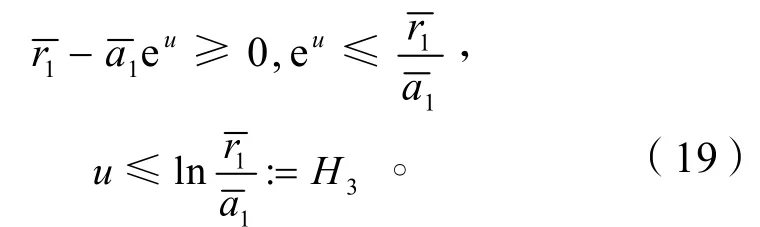
由式（18）第2式得

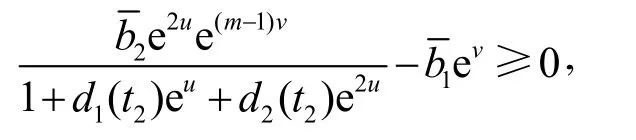
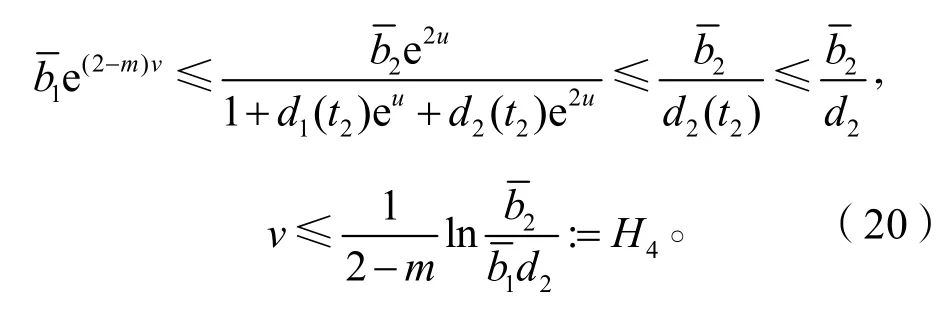
又因式（18）的第1式得

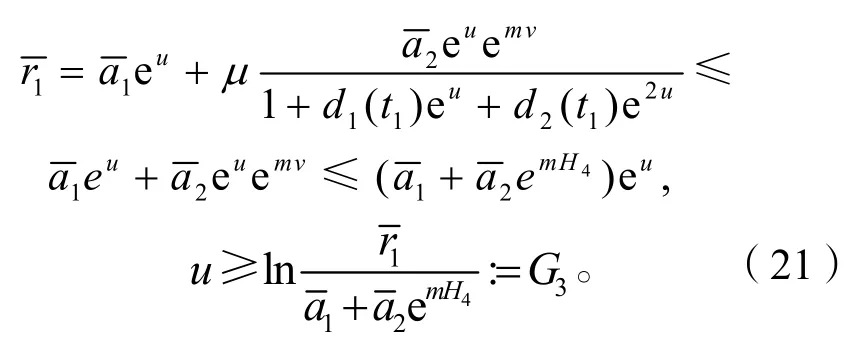
再由式（18）第2式得

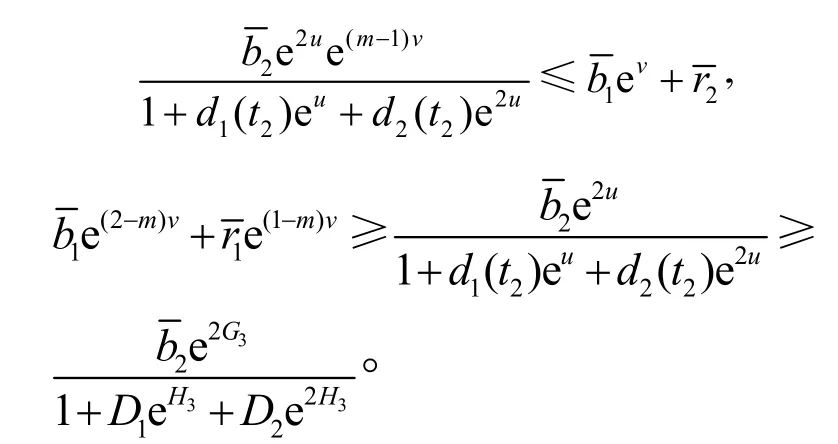
若v≥0，則取0為v的一個下界；

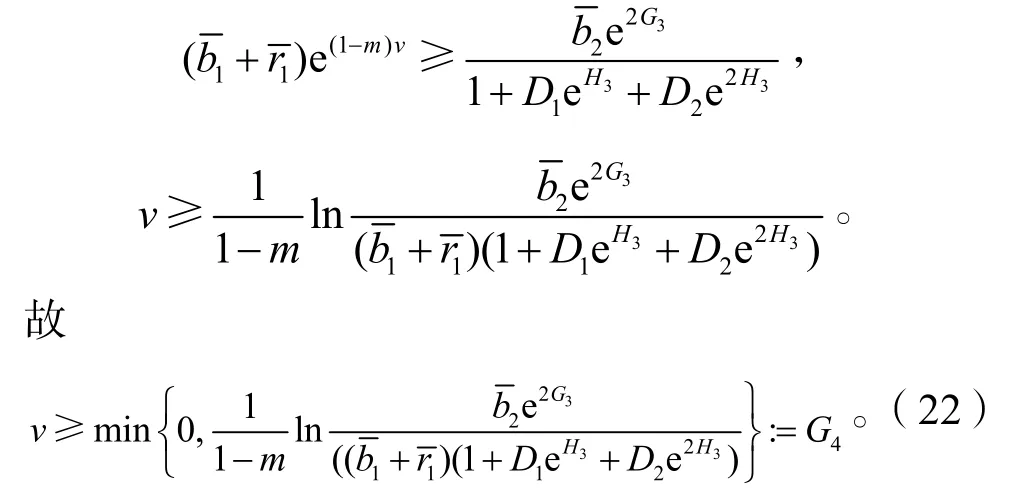
綜合式（19），（20），（21）和式（22）得

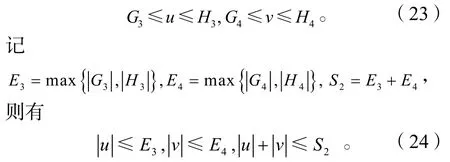
證畢。

定理2.1 系統式（2）至少存在一個正ω-周期解。

令

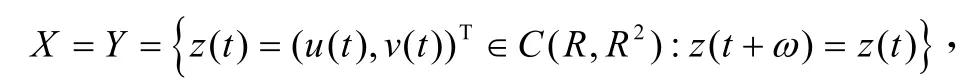
并賦予范數

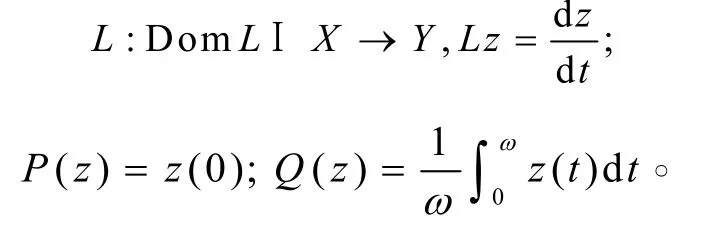
于是有

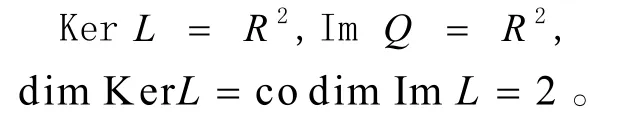
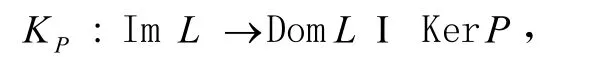
并可求得

所以根據Lebesgue控制收斂定理易證QN和KP（I-Q）N均為連續的。設任一有界開集Ω?X，因在是有界的，所以與都在［0，ω］一致有界且等度連續。根據Arzela-Ascoli定理可知及均為緊致集，因此N在上是L—緊的。特別地，令，我們選取，其中S1，S2由引理2.2及引理2.3的證明式（16-17）、（23-24）所定義，這樣N在上是L—緊的。下面我們驗證引理

2.1（Mawhin'延拓定理）的全部條件。

（i）對于每個

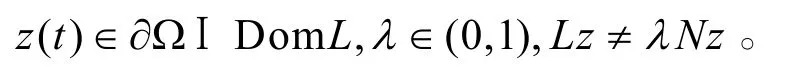
否則，z（t）是系統式（9）的一個正ω-周期解.由引理2.2知，但 z（t）∈?ΩI DomL，從而有，矛盾。

（iii）選擇J:ImQ→KerL，對每個z（t）∈ImQ，使得Jz=z，于是對每個都是一個常向量，并且

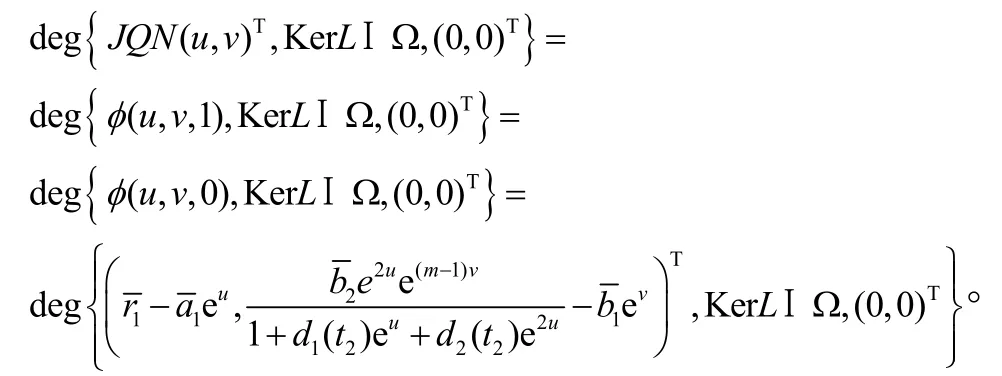
考慮代數方程組

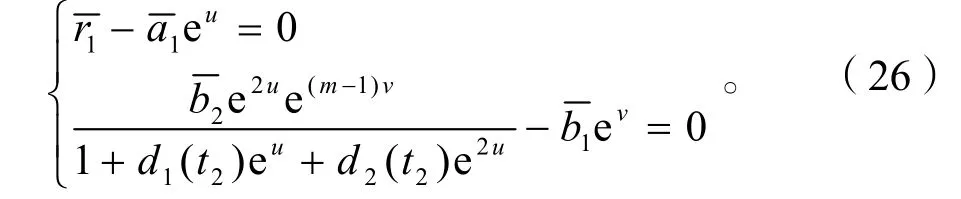
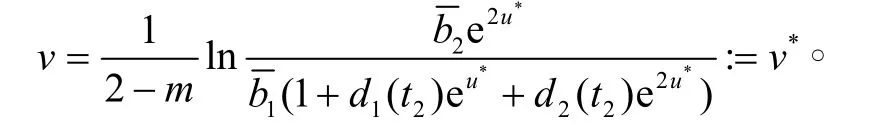
為方便我們引入記號

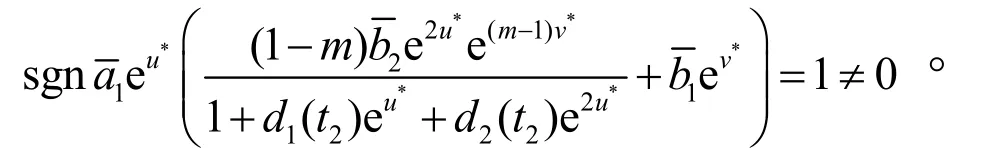
至此，我們驗證了Mawhin的重合度定理的全部條件都滿足，因此系統（3.1）至少有一個正 周期解，從而證明系統式（2）至少有一個正ω-周期解。證畢。

3 系統的全局吸引性

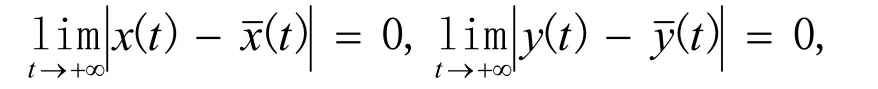
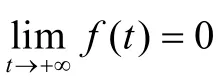
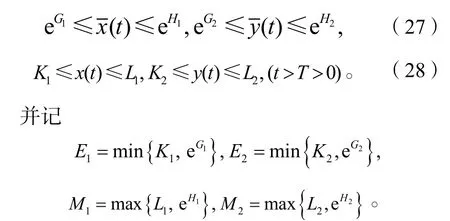
則有

為方便我們引入記號

于是有下面的全局吸引性定理。

定理3.1 如果系統式（2）滿足下列條件：

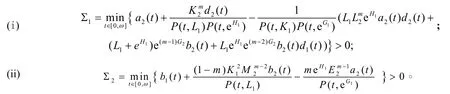
則系統式（2）有且僅有一個正ω-周期解，并且是全局吸引的。

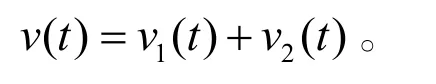
其中

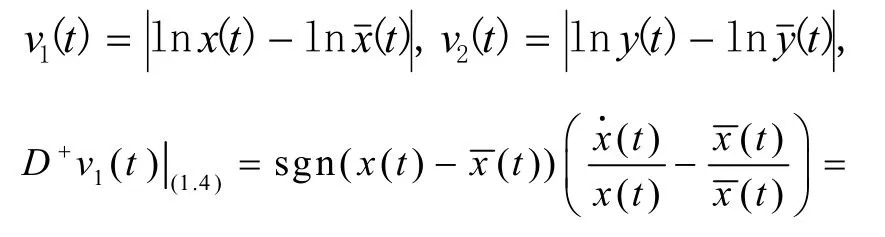
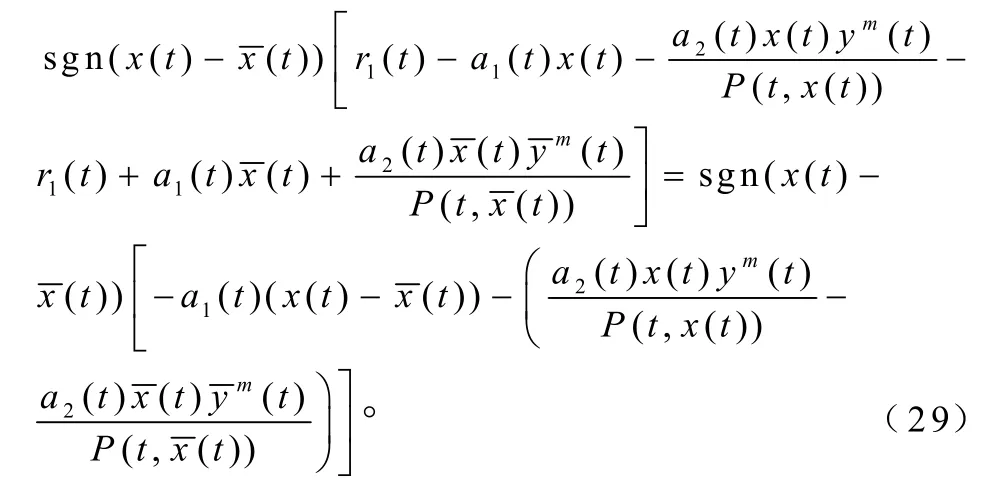
因為

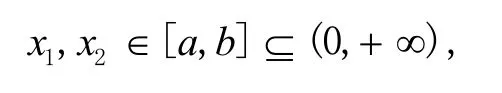
由微分中值定理知

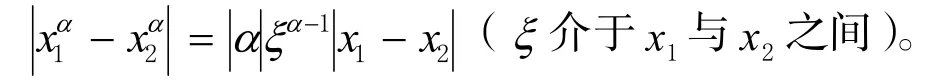
據此，當α＜1時，

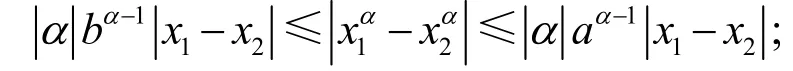
當α＞1時，

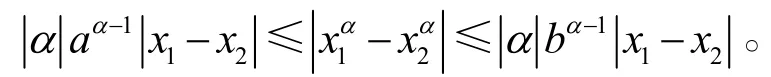
于是由式（31）和式（34）得

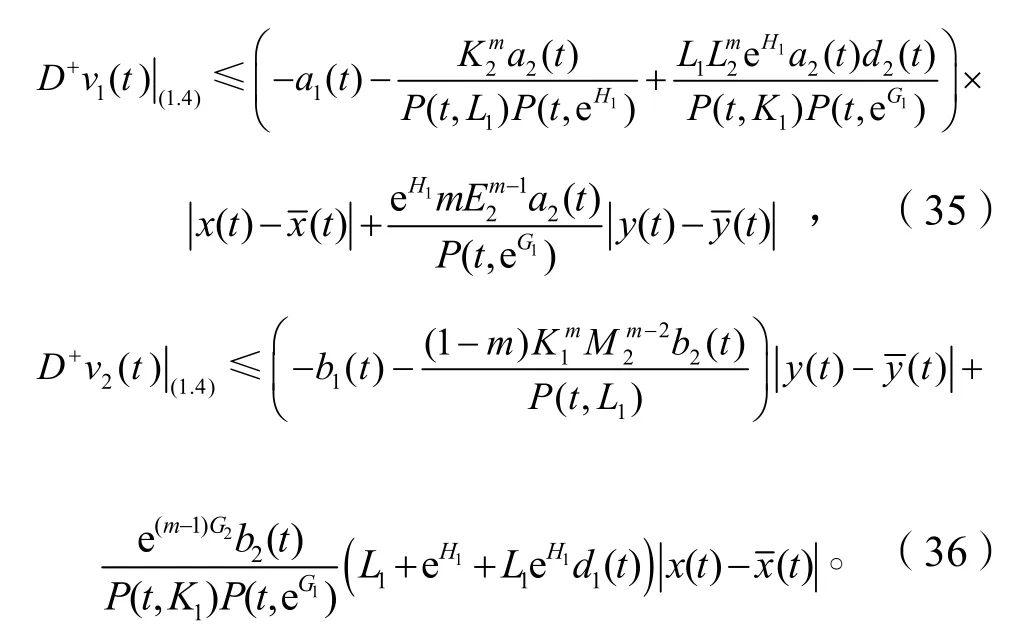
故綜合式（35）和式（36）得

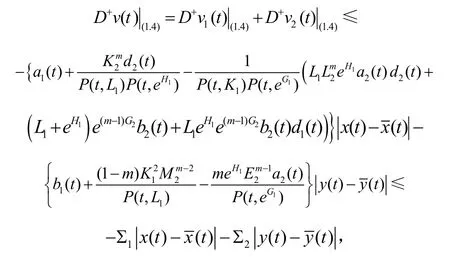
（t＞T＞0，其中T與定理2.1同）。

對上式從T到t積分得

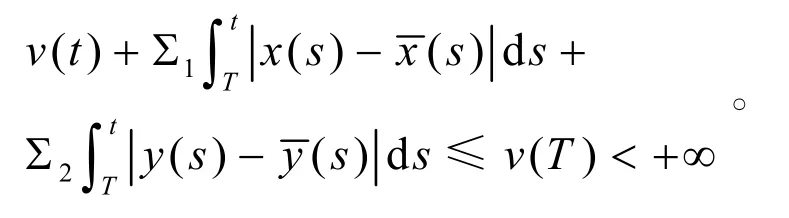
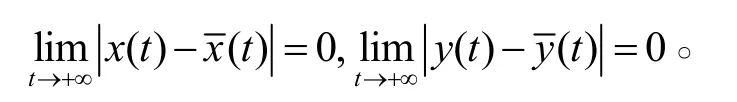
文獻［4］，［5］在證明系統的正周期解全局吸引性時，只對其它初值的周期解證明了是吸引的，而沒有見到證明對系統的任意正解是吸引的。本研究證明了這一結果。

［1］陳蘭蓀.數學生態學模型與研究方法［M］.北京：科學出版社，1998.

［2］ ZHU Y L，WANG K.Existence and global attractivity of positive periodic solution for a predator-prey model with modified Leslie-GowerHolling-type II schemes［J］.Jourmal of mathemtical analysis and applications，2011，384（2）：400-408.

［3］ 黃玉梅.具Holling II類功能反應的時滯擴散模型的全局穩定性［J］.生物數學學報，2006，21（3）：370-376.

［4］ WANG X L，DU Z J，LIANG J.Existence and global attractivity of positive periodic solution to a lotkavolterra model［J］.Nonlinear analysis:real world applications，2010，11（5）:4054-4061.

［5］ Lü Y S，DU Z J.Existence and global attractivity of a positive periodic solution to a lotka-volterra model with mutual interference and holling III type functional response［J］.Nonlinear analysis:real world applications，2011，12（6）:3 654-3 664.

［6］朱晶.有毒物影響和Beddington-DeAngelis型功能反應的捕食系統的全局吸引性［J］.生物數學學報，2013，28（4）:716-724.

［7］ WANG K，ZHU Y L.Global attractivity of positive periodic solution for a Volterra model［J］.Appl Math Comput，2008，203（2）:493-501.

［8］陳蘭蓀，陳鍵.非線性生物動力系統［M］.北京：科學出版社，1993.

［9］ GAINES R E，MAWHIN J L.Coincidence degree and nonlinear differential equations［M］.Berlin:spring-verlag，1977.

［10］ GOPULASAMY K.Stability and oscillations in delay differentialequations ofpopulation dynamics［M］.Dordrecht：kluwer academic publishers，1992.

（責任編輯：任萬森）

GlobalAttractivity of Positive Periodic Solution to a Predator-prey System with Group Defense and HollingⅠⅠⅠType Functional Response

LIU Chang-dong，JIANG Ru，CHAI Hua-jin
（College of Science，Guangdong Ocean University，Zhanjiang 524088，China）

By using the comparison principle of differential equation，Mawhin's continuation theorem of coincidence degree theory and Lyapunov functional，a predator-prey system with mutual interference，group defense and Holling III type functional response is studied.Some results acquired in recent literatures are improved.

Functional response model；Positive periodic solutions；Lyapunov functional；Global attrativity；Mawhin's coincidence theorem

O175.1

A

1673-9159（2016）03-0089-09

10.3969/j.issn.1673-9159.2016.03.015

2016-03-01

劉昌東（1956—），男，副教授，主要研究方向為微分方程穩定性理論，Email：jiru1995@163.com