一種旋轉調制慣導系統的復合旋轉控制算法

鄧志紅,蔡山波,王　博,付夢印,2

(1.北京理工大學自動化學院,北京 100081; 2.南京理工大學,江蘇 南京 210094)

?

一種旋轉調制慣導系統的復合旋轉控制算法

鄧志紅1,蔡山波1,王博1,付夢印1,2

(1.北京理工大學自動化學院,北京 100081; 2.南京理工大學,江蘇 南京 210094)

首先分析了旋轉平臺控制誤差對慣導系統(inertial navigation system,INS)調制效果的影響;然后建立了旋轉平臺的數學模型,結合旋轉調制誤差抑制效果對控制性能的要求,提出了一種自抗擾和滑模變結構相結合的復合旋轉控制方法,該方法充分利用了滑模變結構控制快速減小誤差的優勢和自抗擾控制的精確估計能力,并設計了融合策略。仿真和實驗結果表明,相比于傳統PID控制方法,本文方法減小了旋轉平臺轉速控制誤差,且使反向角度超調誤差和調節時間都減小了50%以上,提高了旋轉調制慣導系統的性能。

旋轉調制; 慣導系統; 誤差抑制; 自抗擾控制; 滑模變結構控制; 復合控制

0　引　言

慣導系統因其自主性和無源性而被廣泛應用于潛艇、艦船中,然而慣導系統的誤差會隨時間不斷積累,其定位精度往往不能滿足長航時潛器的精度要求。旋轉調制技術通過旋轉平臺的周期旋轉,使慣性器件誤差被調制成均值為零的周期變化量,實現對慣性器件常值漂移和慢變誤差的有效抑制,從而提高慣導系統定位精度。旋轉調制技術自19世紀80年代被文獻[1]提出后,得到了廣泛的關注[2-3],國內一些單位也開展了相關研究。國防科技大學在2007年研制出了國內第一臺單軸旋轉慣導系統樣機[4],之后該領域研究工作主要集中在旋轉調制原理分析[5-6]、解算方法[7]、初始對準[8-9]、旋轉方案的設計[10-11]以及誤差標定[12-13]等方面。這些研究都是以假定旋轉平臺理想控制為前提的。但是實際上,旋轉平臺的控制是存在誤差的,文獻[14]從原理上定性地分析了旋轉平臺的控制誤差對調制效果的影響,并且說明了這些影響對于高精度慣導系統來說是不可忽略的,因此,提高旋轉平臺控制精度對于提高長航時定位精度十分必要。

旋轉方案設計是旋轉調制慣導系統領域的研究熱點之一,很多旋轉方案相繼被提出,其中采用最多的是連續正反旋轉和多位置轉停方案。這兩類方案要求旋轉平臺周期地進行換向旋轉、迅速停止和快速啟動。而旋轉平臺作為一個復雜的伺服機構,不平衡力矩、電機力矩波動、轉動慣量變化等因素會給旋轉平臺上述操作帶來很大的干擾。此外,旋轉調制技術要求的工作轉速較低,一般在1(°)/s～50(°)/s之間。低速情況下的非線性摩擦干擾力矩也會嚴重影響旋轉平臺的控制效果。目前,工程上主要采用PID控制算法。PID算法簡單有效,易于實現,但是容易出現超調,且魯棒性不高,響應速度偏低,難以滿足系統高精度的性能要求。文獻[15]提出了一種融合Kalman預測和PID控制的方法,文獻[16]采用了PID和開環控制相結合的方法減小轉臺反向時的超調角,但這兩種方法的魯棒性較弱。文獻[17]采用了神經網絡控制,提高了控制精度,但是它需要通過不斷學習來調整參數,運算量大,對硬件要求高。文獻[18]提出基于干擾觀測器的滑模變結構控制方法,但是干擾觀測器對干擾的抑制能力有限,未補償的干擾易造成滑模控制器的抖振。文獻[19]采用自抗擾控制方法,利用擴張狀態觀測器對干擾的觀測值進行補償,但是響應速度偏慢。

自抗擾技術是在PID控制方法的基礎上發展起來的新型控制技術,控制精度高,魯棒性好,已在很多領域得到應用,如飛行器控制、機器人控制、電機控制等。滑模變結構控制是一種非線性的控制策略,它能使控制對象的狀態軌跡在一定時間內達到預定的滑模面,并沿著滑模面滑動收斂到狀態原點。該控制方法響應速度快,且對被控對象的參數變化和外在干擾等因素具有一定的適應能力,但是它往往因為高頻的切換產生系統抖振。考慮這兩種控制方法各自的優缺點,如果能用一種方法結合它們形成復合控制方法,保留各自的優點,同時抑制各自的缺點,則該復合控制方法既能滿足快速響應的要求,又能保證穩態精度和魯棒性,即達到旋轉平臺的控制要求。根據這一思想并綜合以上文獻,本文提出了基于自抗擾控制和滑模變結構控制的復合控制方法,通過設計融合策略實現在自抗擾控制和滑模變結構控制之間進行平滑切換。

本文首先分析了轉位控制誤差對旋轉調制式慣導系統精度的影響,然后建立了被控旋轉平臺的模型,并據此提出基于自抗擾控制和滑模變結構控制的復合控制方法,最后通過仿真和實驗驗證了所設計算法的可行性。

1　轉位控制誤差對慣導系統定位精度的影響分析

文獻[5]詳細闡述了旋轉調制誤差補償的原理,據此本文將簡單分析轉位控制誤差對導航效果的影響。只考慮單軸旋轉的情況,設坐標系b為載體坐標系,s為IMU坐標系,旋轉軸為方位軸zb,旋轉方案采用連續正反旋轉,每次旋轉一整周,設逆時針旋轉時角速度為正。假設旋轉平臺在正向旋轉一周后角度超調角為θ1,反向旋轉一周后角度超調為θ2,旋轉平臺的旋轉角度為θ,則在一個正反旋轉周期里,陀螺儀的常值漂移誤差ε在載體坐標系b系的積累量為

(1)

可得

(2)

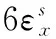
下面分析轉速控制誤差對旋轉調制效果的影響。當旋轉平臺的轉速控制出現誤差時,即實際轉速為ω+δω,該誤差會造成旋轉平臺的轉角誤差,從而導致IMU坐標系到載體坐標系的坐標轉換矩陣產生誤差,即

(3)

因而引起的角速度輸出誤差為

(4)

由上述分析過程可知,因為轉速控制誤差的存在,載體的運動會導致輸出角速度誤差。如果轉速誤差為常值,則在一個旋轉周期內,平臺旋轉的角度也不是整周,可以看作平臺旋轉存在超調角,因而慣性元件的誤差得不到完全的調制。

在以上理論分析的基礎上,本文利用仿真來探討旋轉平臺超調角和轉速控制誤差對慣導系統定位精度的影響。仿真中旋轉方案采用單軸連續正反旋轉,仿真條件設定如下:載體初始緯度為北緯30°,航向為正北方向,加速度計與陀螺的零偏分別為10-4g和0.01(°)/h,各慣性器件標度因數誤差均為10 ppm,各安裝誤差角均為10″。仿真時分別在轉位控制中加入了最大值為50″的超調角和最大幅值為50(″)/s的轉速誤差。經過12 h的導航仿真,存在兩種控制誤差時慣導系統緯度、經度定位誤差分別如圖1、圖2所示。

由圖1、圖2可知,當旋轉平臺的控制有超調角或轉速控制誤差時,緯度定位誤差的波動會更大,經度定位誤差的發散速度更快,因而導致慣導系統的定位精度變差。

綜上所述,旋轉平臺角度控制誤差和轉速控制誤差都會影響旋轉調制的效果,進而影響慣導系統的精度。由于旋轉方案的多樣性,以及旋轉平臺控制誤差的隨機性,無法建立誤差傳播模型來描述這種影響機制,只能進行定性分析,無法用數學方法進行誤差補償。因此,提高旋轉平臺的控制精度和魯棒性對于提高慣導系統的定位精度非常重要。

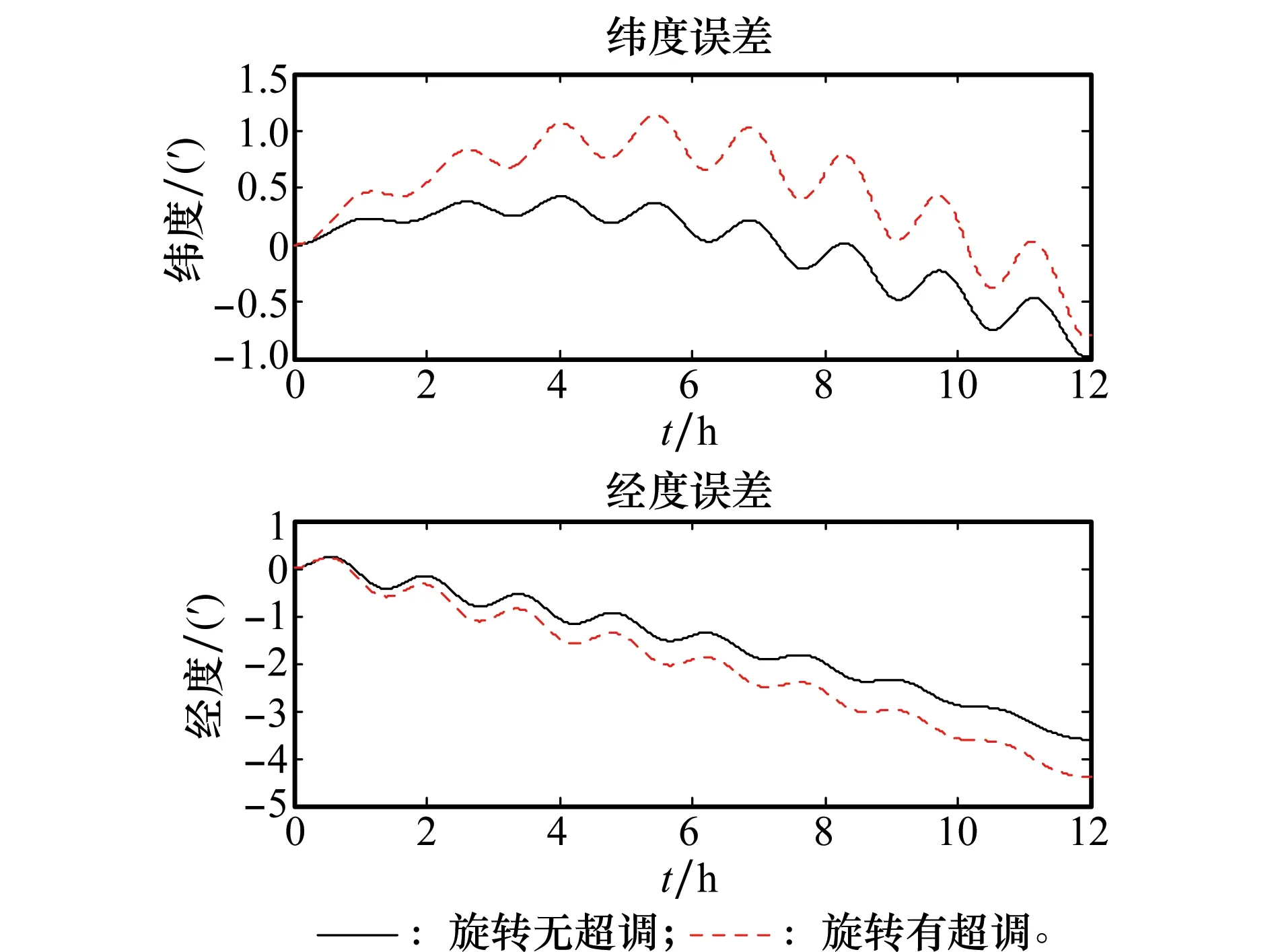
圖1　超調角對定位誤差的影響Fig.1　The influence of angular overshoot on the location accuracy

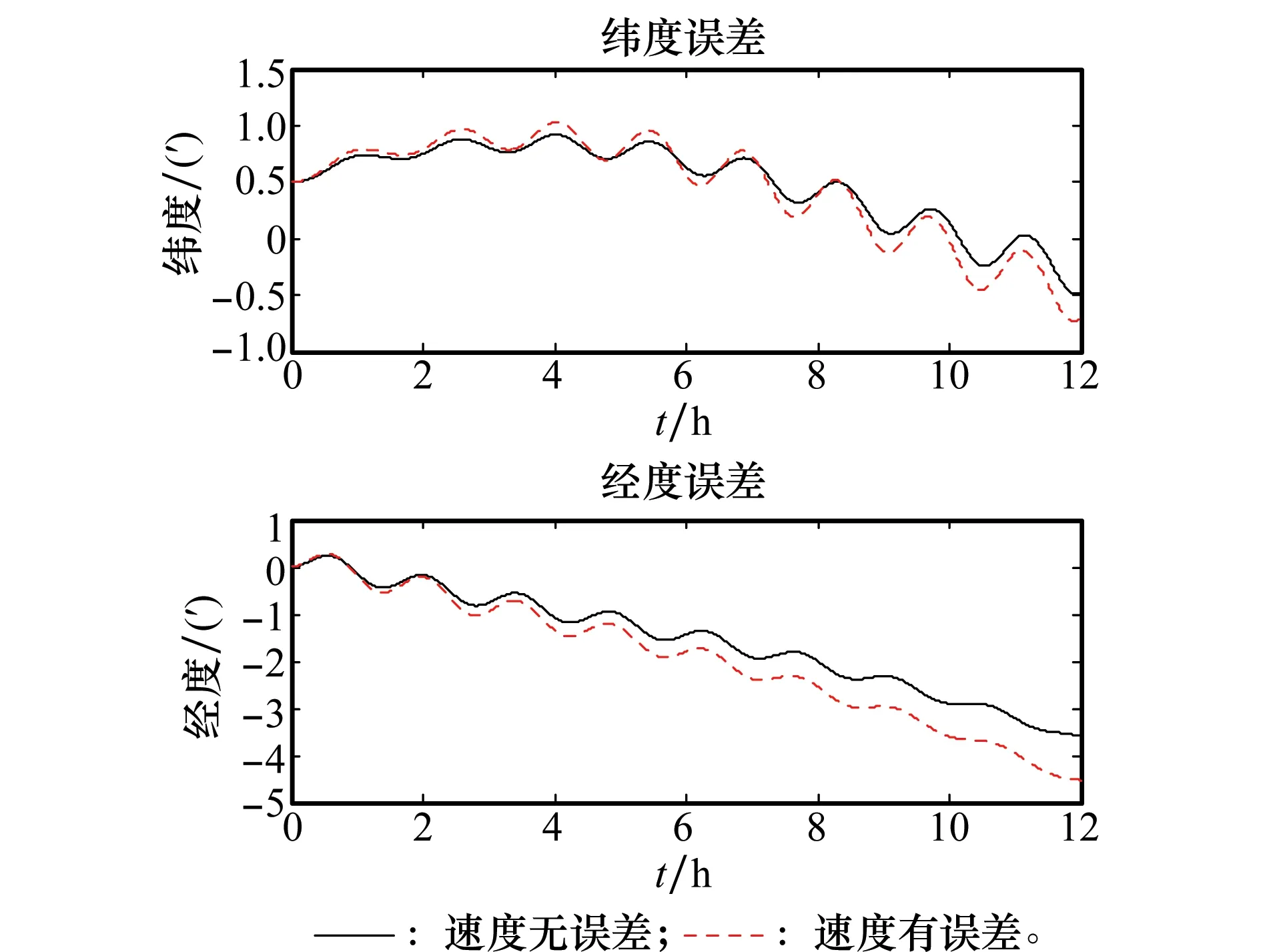
圖2　轉速控制誤差對定位誤差的影響Fig.2　The influence of rotating rate error on the location accuracy

2　旋轉平臺建模

旋轉調制慣導系統中的旋轉平臺由支撐機構、執行元件、傳動裝置、傳感器、控制器等部分組成。每個轉軸的執行元件為直流永磁力矩電機,驅動所負載的旋轉平臺按照既定的旋轉方案運行。根據動力學方程,可建立單轉軸的數學模型:

(5)

式中,θ是旋轉平臺的轉角;J為轉軸上負載的轉動慣量(在本系統中,包括電機轉軸和旋轉平臺等裝置的轉動慣量總和);kT=kt/Ra;kt為電磁轉矩系數;Ra為電樞回路總電阻;kp為功率放大器放大倍數;ke為反電勢常數;Md為旋轉平臺干擾力矩;ur為外界輸入控制電壓。

將上述模型轉化為狀態方程的形式,可得狀態空間數學模型

(6)

其中

在實際工程控制中,進行仿真研究和計算機實時控制的都是離散系統。因此將式(6)離散化,得

(7)

3　復合控制算法設計

旋轉平臺需要高精度的位置控制和快速的響應能力。本文提出了一種基于自抗擾控制和滑模變結構控制的復合控制算法。自抗擾控制器可以通過擴張狀態觀測器對被控對象的內擾和外擾進行觀測,然后通過輸入量對這些干擾進行補償,提高控制精度和魯棒性。跟蹤微分器雖然在一定程度上可以緩解快速性和超調之間的矛盾,但犧牲了響應的快速性。滑模變結構控制響應速度比較快,但存在抖振的問題,對控制效果影響很大。基于自抗擾控制和滑模變結構控制的復合控制方法將結合這兩種控制方法的優點,抑制其缺點,保證系統反應快速性的同時,也能保證系統的精度,避免產生強烈的抖振。

3.1自抗擾控制器的設計

自抗擾控制器主要由跟蹤微分器、擴張狀態觀測器和非線性反饋控制器3部分組成。根據第2部分建立的對象模型,分別設計自抗擾控制器。

3.1.1跟蹤微分器的設計

跟蹤微分器的作用是對輸入信號進行快速跟蹤,安排一個合適的過渡過程,緩解超調和快速性之間的矛盾,同時它還可以獲取輸入信號的微分信號,并有一定的濾波能力,抑制輸入信號中的噪聲成分。設計離散跟蹤微分器如下:

(8)

式中,fhan為最速綜合控制函數,實現形式如下:

fhan(x1,x2,r0,h)=

(9)

式中,v1、v2分別是輸入信號的跟蹤信號及其微分信號,是跟蹤微分器的輸出;h為積分步長;h0是濾波因子;r0是速度因子。

3.1.2擴張狀態觀測器的設計

擴張狀態觀測器是自抗擾控制器的核心。它將系統的不確定干擾項擴張成一個新的狀態量,然后對所有狀態量進行觀測,輸出估計值,然后進行實時補償。針對被控對象模型,設計線性離散擴張狀態觀測器:

(10)

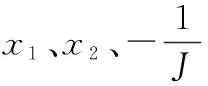
3.1.3非線性反饋控制器的設計

非線性反饋控制器的作用主要是根據輸入的誤差信息通過非線性加權方法得到控制量。經典的設計方法在求取控制誤差時,都是用跟蹤微分器的輸出和擴張狀態觀測器的觀測輸出做差得到的,而是采用如下模型:

(11)

這樣做的好處是控制算法不要求控制對象的狀態量都可被傳感器檢測。但是對于本文研究對象,旋轉平臺的位置和轉速輸出都可檢測,因此可以直接用系統的輸出同跟蹤微分器的輸出做差,提高精確度。據此,設計離散非線性反饋控制器:

(12)

其中

然后根據觀測器對干擾的估計值,進行實時干擾補償:

(13)

式中,α1、α2、δ1、β1、β2為可調參數,δ1決定線性區間大小,參數β1和β2的作用類似于PD控制器中的系數。

由上可知,自抗擾控制器的可調參數比較多,而目前沒有系統和理論性的參數整定方法,在實際運用中,可根據工程經驗設定參數,再進行微調。具體設定方法如下。

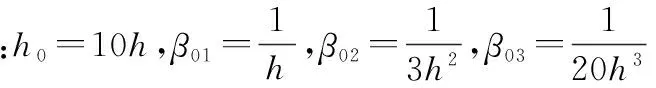
3.2滑模變結構控制器設計

滑模運動通常包括兩個部分:第一部分是趨向滑模面的運動,第二部分是沿著滑模面的運動。本文采用了基于指數趨近率的離散滑模控制,該控制可以保證系統在開始響應階段快速向滑模面運動,縮短趨近時間,并且靠近滑模面時速度很小,從而改善了系統的動態品質。該控制策略要求切換函數s(k)滿足以下要求:

(14)

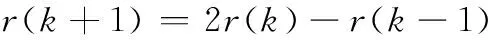
dr(k+1)=2dr(k)-dr(k-1)

(15)

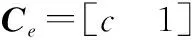
(16)

根據控制對象的離散模型(7),有

(17)

根據式(16)和式(17),可以得到

(18)

式中,可調參數有c、ε、q。其中c決定線性滑模面的斜率,其值越大,滑模運動段響應速度越快;q主要影響切換函數動態過渡過程,適當調整該參數能夠改變系統向滑模面的趨近速度,其值越大,到達滑模面的速度越快;ε是影響系統克服攝動及外干擾的主要參數,其值越大,克服干擾的能力越強。在進行參數設定和調整時,可根據以上每個參數各自的作用和實際控制效果進行。

CeLZd(k)-s(k)+εTsgn(s(k))+qTs(k))

(19)

3.3融合策略設計

本文采用的融合策略是在系統響應初始階段或控制誤差比較大時,主要采用滑模變結構控制,使系統盡快趨向滑模面;隨著控制誤差的減小,逐漸采用自抗擾控制方法,保證系統的穩態精度,減小超調,盡量避免抖振的發生。采用的具體融合方法為

(20)

其中

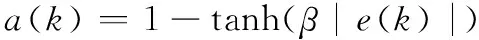
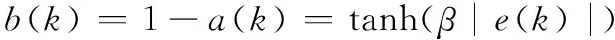
(21)

式中，ur(k)為控制器輸出控制量；參數β為融合因子。函數tanh(β|x|)的曲線如圖3所示。從圖3可以看出,當β取不同的值時,函數從0～1上升的速率存在差異,在式(20)中,它決定了控制器中兩種控制量所占的比例。

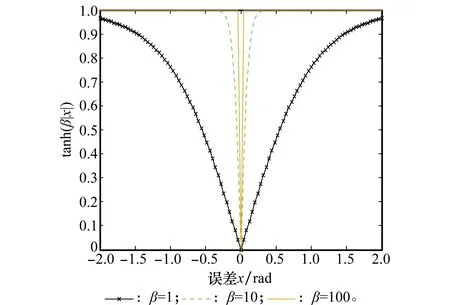
圖3　融合因子設計Fig.3　The design of fusion factor

4　仿真與實驗驗證

4.1仿真驗證

在Simulink仿真平臺上驗證本文所設計算法的可行性。為了更真實地反映實際系統的工作情況,本文在仿真時采用 Stribeck模型對摩擦力矩進行建模,將摩擦力矩作為干擾的一部分。具體模型如下:

(22)

(23)

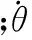
除了非線性摩擦力矩干擾外,旋轉平臺在工作時還會受到諸如不平衡力矩等其他擾動,在仿真時加入正弦函數形式的信號作為干擾信號,檢驗控制算法的抗干擾能力。控制對象和摩擦模型的參數來源于實驗室的實驗設備,如表1所示。自抗擾控制和滑模變結構控制器的參數以及融合因子如表2所示。

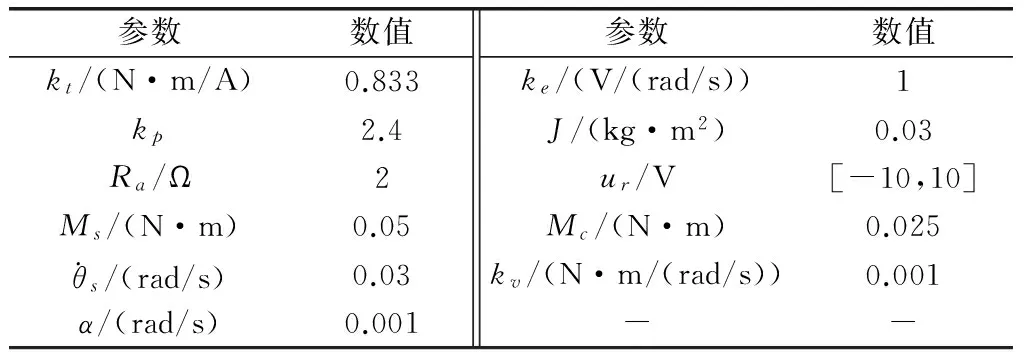
表1　控制對象參數

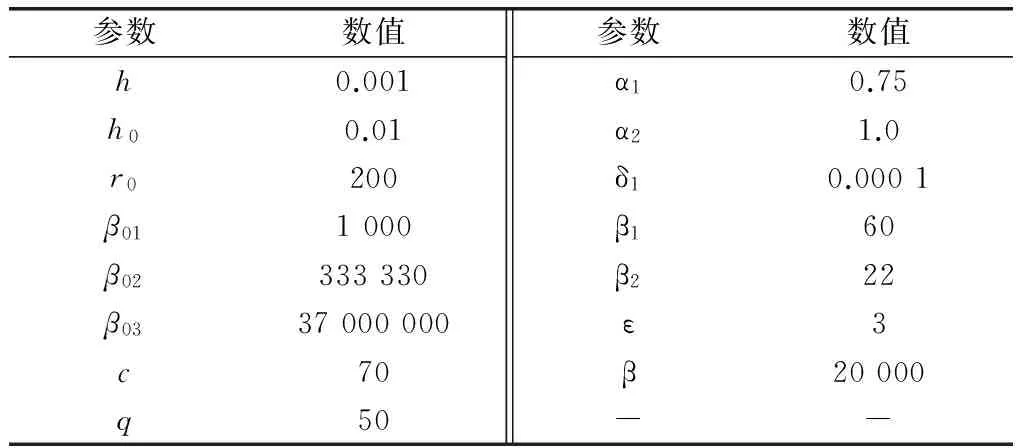
表2　控制器參數

目前工程上采用最多的旋轉方案是連續正反旋轉和多位置轉停方案,這兩種方案涉及到旋轉、反向和轉停3種運動,因此在仿真時輸入參考信號主要模擬了這3種運動方式。轉速為1(°)/s,仿真控制周期為T=1 ms。在相同的仿真條件下,采用了PID控制、自抗擾控制和滑模變結構控制3種算法分別進行對比仿真。圖4是平穩旋轉時的角速度誤差比較圖。

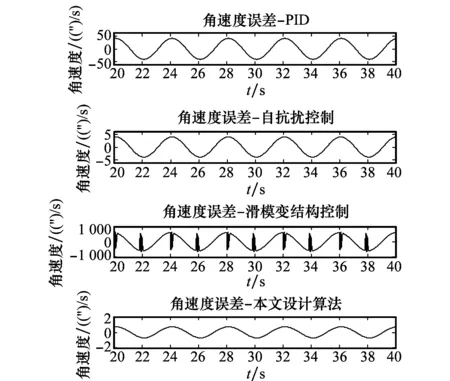
圖4　穩態跟蹤角速度誤差Fig.4　Comparison of steady angular speed errors

圖5是在旋轉平臺換向時的超調角比較圖。圖6是旋轉平臺在靜止狀態下的抖振情況比較圖。綜合這4種控制方法的控制效果,如表3所示。

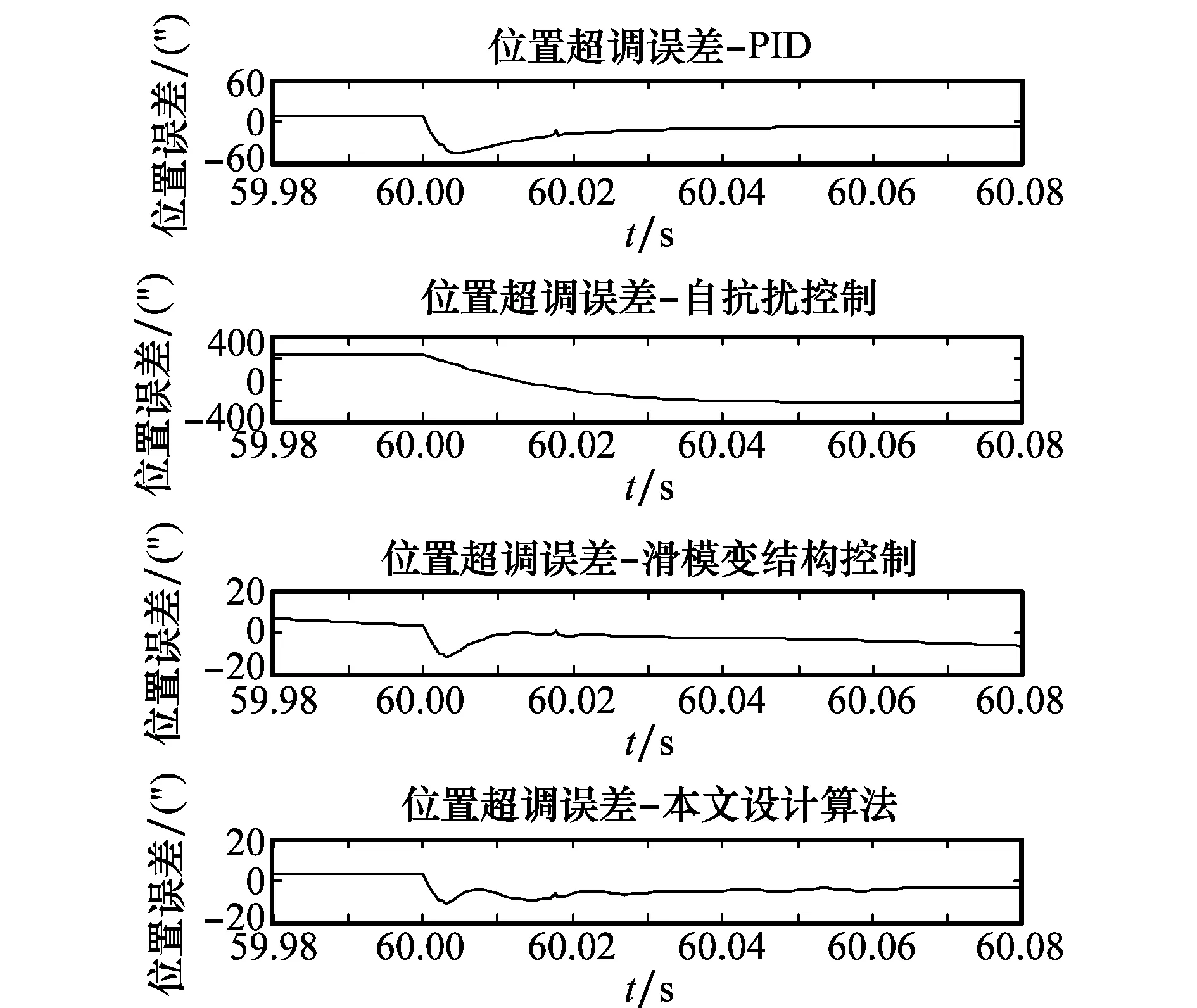
圖5　換向超調角誤差Fig.5　Comparison of reversing angular overshoots errors

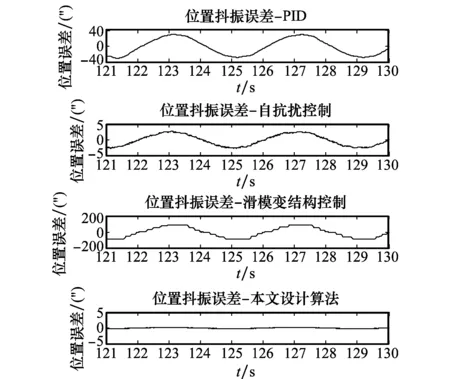
圖6　抖振誤差Fig.6　Comparison of chattering errors

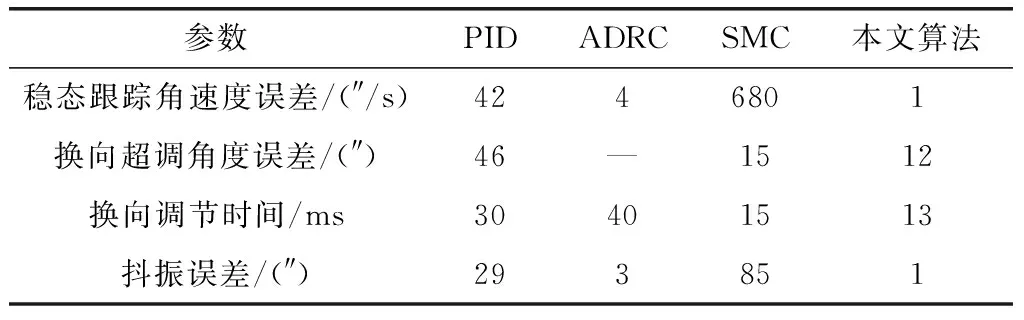
參數PIDADRCSMC本文算法穩態跟蹤角速度誤差/(″/s)4246801換向超調角度誤差/(″)46—1512換向調節時間/ms30401513抖振誤差/(″)293851

注1)：表中誤差值均為最大值。

從圖4～圖6和表3可知,較傳統PID算法而言,本文所提出的復合控制算法減小了旋轉平臺平穩運行時的轉速波動誤差,并且反向時的平臺超調角和調節時間都減少50% 以上,實現了平臺的快速反轉;同時,基本抑制了滑模變結構控制因高頻切換造成的抖振。因此,所設計的復合控制算法提高了旋轉平臺的控制精度。

4.2實驗驗證

采用實驗室的開放式雙軸旋轉慣導系統(見圖7)作為實驗平臺。在相同的條件下,分別采用傳統的PID算法和本文所提出的復合控制算法進行對比實驗。慣導系統的定位誤差如圖8所示。

圖7　開放式雙軸旋轉慣導系統Fig.7　The open Dual-axis rotational INS

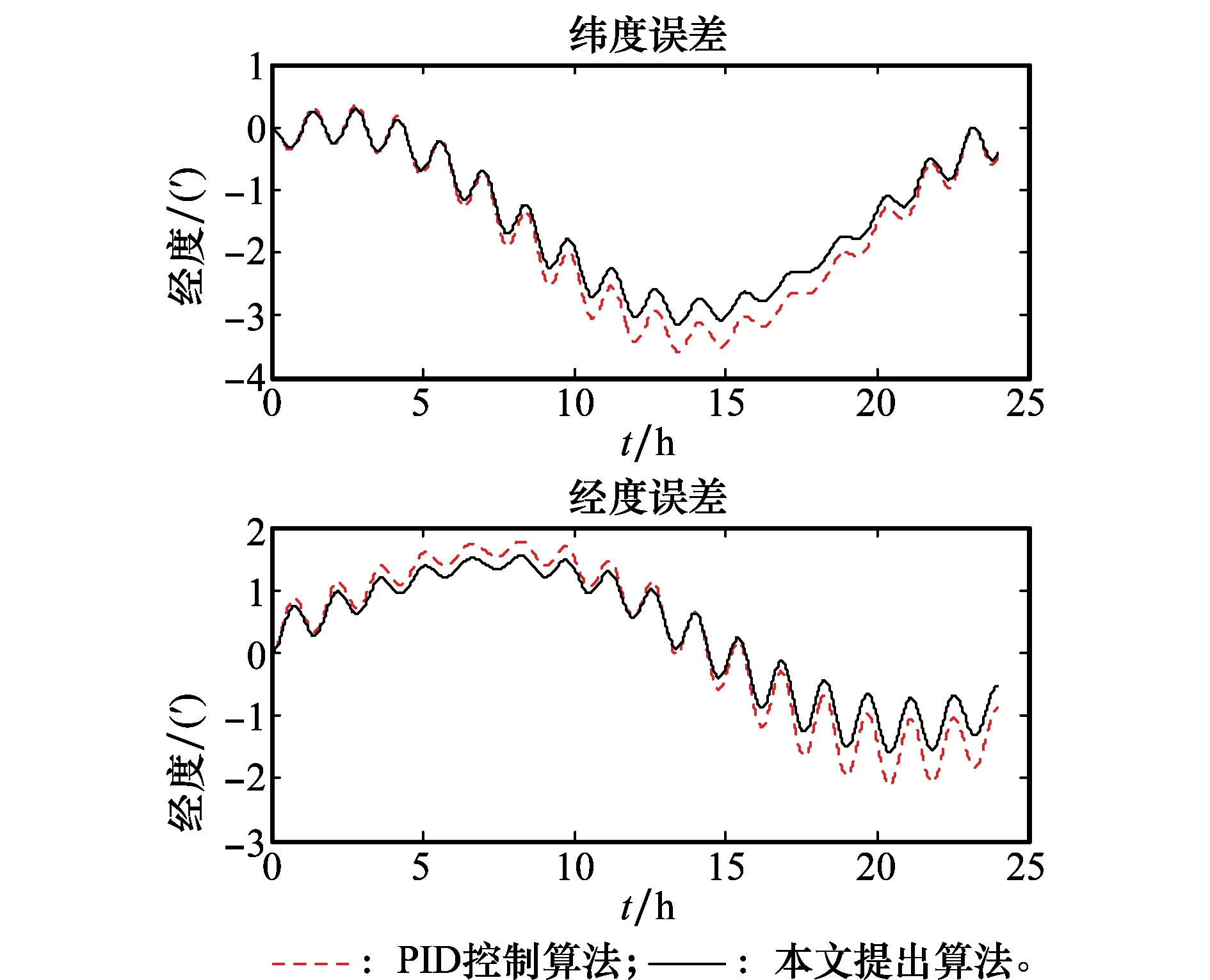
圖8　實驗結果對比Fig.8　Comparison of experimental results

由圖8可知,與采用傳統PID算法控制旋轉平臺的旋轉慣導系統相比,采用本文算法的旋轉慣導系統減小了定位誤差,從而提高了慣導系統的定位精度。

5　結　論

本文分析了轉位控制誤差對慣導系統誤差調制效果的影響,明確了平臺超調角、轉速波動等控制誤差對旋轉調制慣導系統精度的影響。通過對被控旋轉平臺特性的研究,提出了自抗擾控制和滑模變結構復合控制算法,設計了融合策略,仿真和實驗結果證明了該算法的有效性,它既能實現快速響應,減小調節時間,又能保證系統的控制精度,減小超調角,從而減小了旋轉平臺轉位控制誤差對旋轉調制效果的影響,提高了旋轉慣導系統的定位精度。

[1] Levinson E,Jr Giovanni C S.Laser gyro potential for long endurance marine navigation[C]//Proc.of the IEEE Position Location and Navigation Symposium,1980:115-129.

[2] Levinson E,Majure R.Accuracy enhancement techniques applied to the marine ring laser inertial navigator(MARLIN)[J].Proc.of the Navigation,1987,34(1):64-86.

[3] Lahham J,Brazell J.Acoustic noise reduction in the MK 49 ship’s inertial navigation system (SINS)[C]//Proc.of the IEEE Position Location and Navigation Symposium,1992:32-39.

[4] Yu X D,Wang Y,Zhang P F,et al.Influence of single-axial rotation on INS error characteristics[J].Journal of Chinese Inertial Technology,2008,16(6):643-648.(于旭東,王宇,張鵬飛,等.單軸旋轉對慣導系統誤差特性的影響[J].中國慣性技術學報,2008,16(6):643-648.)

[5] Yuan Z G,Zhao L.Error analysis of rotary SINS sensor[J].Sensors & Transducers,2013,156(9):35-39.

[6] Deng Z H,Sun M,Wang B.Error modulation scheme analysis of dual-axis rotating strap-down inertial navigation system based on FOG[C]//Proc.of the 33rd Chinese Control Conference,2014:692-696.

[7] Zhang L D,Lian J X,Wu M P,et al.An improved computation scheme of strapdown inertial navigation system using rotation technique[J].Journal of Central South University,2012,19(5):1258-1266.

[8] Chen G,Wang W.Initial alignment of rotation modulation SINS based on improved open loop gyrocompass method[C]//Proc.of the 3rd International Conference on Intelligent Control and Information Processing,2012:264-267.

[9] Zhou Z,Huang F R,Sun W Q,et al.Nonlinear initial alignment method of dual-axis rotary SINS[J].Journal of Chinese Inertial Technology,2011,19(4):408-412.(周喆,黃鳳榮,孫偉強,等.雙軸旋轉式SINS非線性初始對準方法[J].中國慣性技術學報,2011,19(4):408-412.)

[10] Sun F,Sun W.Research on auto-compensation by rotation in strapdown inertial navigation systems[J].Systems Engineering and Electronics,2010,32(1):122-125.(孫楓,孫偉.旋轉自動補償捷聯慣導系統技術研究[J].系統工程與電子技術,2010,32(1):122-125.)

[11] Li A,Chang G B,Qin F J,et al.Improved precision of strapdown inertial navigation system brought by dual-axis continuous rotation of inertial measurement unit[C]//Proc.of the 2nd International Asia Conference on Informatics in Control,Automation and Robotics,2010:254-287.

[12] Wang B,Ren Q,Deng Z H,et al.A self-calibration method for non-orthogonal angles between gimbals of rotational inertial navigation system[J].IEEE Trans.on Industrial Electronics,2015,62(4):2353-2362.

[13] Ren Q,Wang B,Deng Z H,et al.A multi-position self-calibration method for dual-axis rotational inertial navigation system[J].Sensors and Actuators A:Physical,2014,219:24-31.

[14] Zha F,Xu J N,Huang Z H,et al.Analysis and compensation for rotary errors of INS with single axis rotation[J].Journal of Chinese Inertial Technology,2012,20(1):11-16.(查峰,許江寧,黃寨華,等.單軸旋轉慣導系統旋轉性誤差分析及補償[J].中國慣性技術學報,2012,20(1):11-16.)

[15] Wang W B,Zhao P B.Application of Kalman filter in the CNC servo control system[J].Procedia Engineering,2010,7:442-446.

[16] Liu F,Wang W,Zhang Z Y,et al.Motor rotation control method for rotation-modulation SINS[J].Electric Machines and Control,2012,16(11):17-21.(劉芳,王瑋,張仲毅,等.用于旋轉調制捷聯慣導系統的旋轉控制方法[J].電機與控制學報,2012,16(11):17-21.)

[17] Hu H J,Yue J Y,Zhan P.A control scheme based on RBF neural network for high-precision servo system[C]//Proc.of the International Conference on Mechatronics and Automation,2010:1489-1494.

[18] Takeichi K,Yamada H,Muto T.Sliding mode control using a disturbance observer for an electro-hydraulic servo system[J].Transactions of the Japan Hydraulics & Pneumatics Society,2001,32(4):91-97.

[19] Hu H J,Li C C.The design of target movement simulation system based on auto-disturbance rejection controller[C]//Proc.of the International Conference on Automatic Control and Artificial Intelligence,2012:2103-2106.

Compound rotation control algorithm for rotational INS

DENG Zhi-hong1,CAI Shan-bo1,WANG Bo1,FU Meng-yin1,2

(1.School of Automation,Beijing Institute of Technology,Beijing 100081,China; 2.Nanjing University of Science and Technology,Nanjing 210094,China)

Firstly,the modulation influence of rotational platform’s control error on the inertial navigation system (INS)is analyzed.Then,based on the mathematical model of the rotational platform and the control requirements for the rotation modulation technology,a compound algorithm based on active disturbance rejection control (ADRC)and sliding model control (SMC)is put forward.The compound algorithm takes full advantage of SMC’s superiority to decrease control error and ADRC’s ability to estimate system states.Meanwhile,a fusion strategy is designed.The simulation and experiment results show that compared with the traditional PID method,the proposed algorithm decreases the speed error of the platform,and minishes the angular overshoot and responding time more than 50% when changing the rotation direction.

rotation modulation; inertial navigation system (INS); error depressing; active disturbance rejection control (ADRC); sliding model control (SMC); compound control

2015-06-09；

2015-12-07；網絡優先出版日期：2016-06-02。

國家重點基礎研究發展計劃(973計劃)(61321902)；國家自然科學基金(61422102，61127004)資助課題

U 666.12

ADOI:10.3969/j.issn.1001-506X.2016.11.23

鄧志紅(1974-),女,教授,博士,主要研究方向為導航制導與控制。

E-mail:dzh_deng@bit.edu.cn

蔡山波(1991-),男,碩士,主要研究方向為導航制導與控制。

E-mail:shanbocai@126.com

王博(1982-),男,副教授,博士,主要研究方向為導航制導與控制。

E-mail:wb1020@bit.edu.cn

付夢印(1964-),男,教授,博士,主要研究方向為導航制導與控制。

E-mail:fumy@bit.edu.cn

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160602.1525.002.html