基于Kriging模型的武器站炮口擾動優化

鄧威， 毛保全， 馮帥， 李程

(裝甲兵工程學院 兵器工程系， 北京 100072)

?

基于Kriging模型的武器站炮口擾動優化

鄧威， 毛保全， 馮帥， 李程

(裝甲兵工程學院 兵器工程系， 北京 100072)

炮口擾動是影響頂置武器站射擊精度的重要因素。為研究抑制炮口擾動的技術途徑，基于有限元理論建立頂置武器站剛柔耦合動力學模型，并通過射擊精度試驗驗證了該模型的準確性。以炮口擾動綜合函數為優化目標，構建頂置武器站炮口擾動優化設計模型，應用Kriging序列優化算法實現優化問題的求解。仿真結果表明，考慮部件柔性變形的有限元模型符合真實系統的振動特性，Kriging序列優化算法能夠快速有效地用于武器站炮口擾動優化問題的求解。尋優得到的全局最優解，能使頂置武器站炮口擾動得到有效抑制。

兵器科學與技術； 頂置武器站； 炮口擾動； 有限元模型； Kriging序列優化

0　引言

頂置武器站是可配備多種武器和不同組合火力控制系統，可搭載于不同軍用車輛及平臺的模塊化武器系統[1]。目前，頂置武器站在國內屬于新型武器系統，由試驗樣機來看，其射擊精度還有待提高。為全面掌握頂置武器站動力學特性及提高射擊精度，相關工程人員致力于頂置武器站的理論研究。徐禮[2]以某型武器站為研究對象，基于剛柔耦合多體動力學，采用多學科協同仿真方法，對武器站射擊時的動態響應進行分析；田發達等[3]針對武器站射擊精度不高的問題，基于多體動力學仿真軟件ADAMS建立武器站發射動力學模型，并就不同射擊工況對武器站炮口擾動的影響規律進行分析；張海燕等[4]建立了某型武器站的立靶密集度參數化仿真模型，并以射彈立靶坐標為目標函數，對武器站結構參數進行靈敏度分析。

以上文獻表明：一方面，身管類武器系統對發射彈丸的擾動最終反映在炮口上，彈丸出炮口時刻炮口的振動狀態直接影響著彈丸的初始運動姿態，因此，炮口擾動是影響身管類武器系統射擊精度的重要因素[5]，通過抑制炮口擾動以提高射擊精度是有效且可行的；另一方面，目前國內對頂置武器站進行的理論研究主要是利用動力學仿真軟件進行真實武器系統的動力學建模、基于動力學模型進行武器系統的影響規律分析以及基于動力學模型進行結構優化設計等常規動力學分析方法，而該常規方法在建立武器系統動力學模型時，往往為了貼近實際物理過程而面面俱到地建立動力學模型，導致應用該模型進行下一步分析或優化時帶來巨大負擔。因此，有必要采取一種行之有效的措施以提高優化效率。

Kriging代理模型技術是解決上述問題的有效途徑，其通過試驗設計及統計分析手段建立起復雜原函數的近似模型[6]，通過對代理模型進行尋優求解，能大大提高優化效率。目前，Kriging模型已在化工、航天、水利等多個領域都得到成功應用。王曉強等[7]引入Kriging模型對苯乙烯裝置的流程進行優化，優化結果有效降低了流程運行費用；周算等[8]基于Kriging模型建立起典型結構計算屈曲載荷的工程方法；何歡等[9]以薄壁管為研究對象，基于Kriging模型提出了耐撞性優化方法；鄧志平等[10]將Kriging模型應用于土體參數空間變異性邊坡的可靠度分析。然而，對于火炮領域，將Kriging模型應用于剛柔耦合動力學模型炮口擾動優化的相關文獻還鮮有介紹。

本文基于Kriging模型對頂置武器站炮口擾動進行優化。基于有限元理論建立頂置武器站剛柔耦合發射動力學模型，以炮口擾動綜合量為目標函數，以緩沖器阻尼、身管彈性模量及泊松比為設計變量，以應力幅值及后坐位移為約束條件，建立武器站炮口擾動優化設計模型，并利用Kriging序列優化算法實現優化問題的求解，為提高武器站射擊精度提供參考。

1　頂置武器站剛柔耦合動力學模型

頂置武器站發射過程是一個集內彈道、機械振動、材料力學等多學科于一身的復雜過程，在射擊載荷的作用下，身管、耳軸、托架等主要受力部件會發生不同程度的柔性變形，從而對武器系統乃至炮口的振動特性產生重要影響。因此，有必要考慮柔性非線性的影響，構建頂置武器站剛柔耦合動力學模型，以符合真實系統發射過程的動力學特性。

1.1基于模態坐標的柔性體描述

當忽略阻尼的影響且柔體為自由振動時，空間柔體的運動方程[11]可以簡化為

Mx″(t)+Kx(t)=0，

(1)

式中：M為質量矩陣；K為剛度矩陣；x″(t)為節點的加速度向量；x(t)為節點的位移向量。

由于運動微分方程往往存在彈性耦合或慣性耦合，使得方程難以求解，為此，可以引入模態坐標對解空間進行線性變換。

原微分方程解的形式為

xi=φisin (ωt+θ),i=1,2,…,n，

(2)

式中：φi為振型幅值；ω為模態頻率；θ為相位角；n為空間柔體所包含的自由度數。

將其代入微分方程(1)式，并令λ=ω2，整理得

(-λM+K)Φ=0.

(3)

(3)式是關于向量Φ的齊次代數方程，其存在非零解的充分必要條件是系數矩陣的行列式為0，即有

|-λM+K|=0.

(4)

(4)式行列式展開后是關于λ的n次多項式，同時也是該n自由度系統的特征方程，其存在n個特征值λi以及對應著n個特征向量φi：

λiMφi-Kφi=0,i=1,2,…,n.

(5)

特征向量之間存在加權正交關系，即對于不同的特征向量φi和φj，有

(6)

mi和ki分別為模態質量和模態剛度，也稱為廣義質量和廣義剛度。

作坐標變換x=Φq并代入(1)式得

MΦq″(t)+KΦq(t)=0.

(7)

對(7)式兩邊同時乘以特征向量的轉置矩陣ΦT，并整理得

mq″(t)+kq(t)=0.

(8)

此時，在模態空間下，系數矩陣均為對角矩陣，原運動微分方程實現解耦。

1.2武器站剛柔耦合動力學模型

根據武器站發射過程部件受力特點，將身管、支撐架、托架、耳軸等主要受力且對炮口擾動影響較大的部件處理為柔性體，相關部件的網格模型如圖1～圖4所示。基于多體動力學仿真軟件ADAMS構建頂置武器站剛柔耦合動力學模型，如圖5所示。

圖1　身管有限元模型Fig.1　Finite element model of barrel

圖2　支撐架有限元模型Fig.2　Finite element model of support frame

圖3　耳軸有限元模型Fig.3　Finite element model of trunnion

圖4　托架有限元模型Fig.4　Finite element model of base structure

圖5　武器站剛柔耦合動力學模型Fig.5　OWS rigid flexible coupling dynamic model

1.3試驗驗證

為檢驗頂置武器站剛柔耦合動力學模型的準確性，對比分析實物樣機的射擊精度試驗數據及仿真數據。對武器站進行固定于地面的200 m單發立靶密集度試驗，試驗現場如圖6所示，測試點如圖7所示，測試數據包括武器站不同部位的振動加速度及后坐運動特征參數，實測數據與仿真數據的對比如圖8、圖9、表1所示。

圖6　射擊試驗現場Fig.6　Firing test site

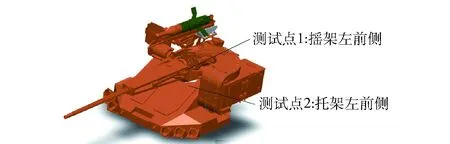
圖7　測試點布置圖Fig.7　Layout of test points

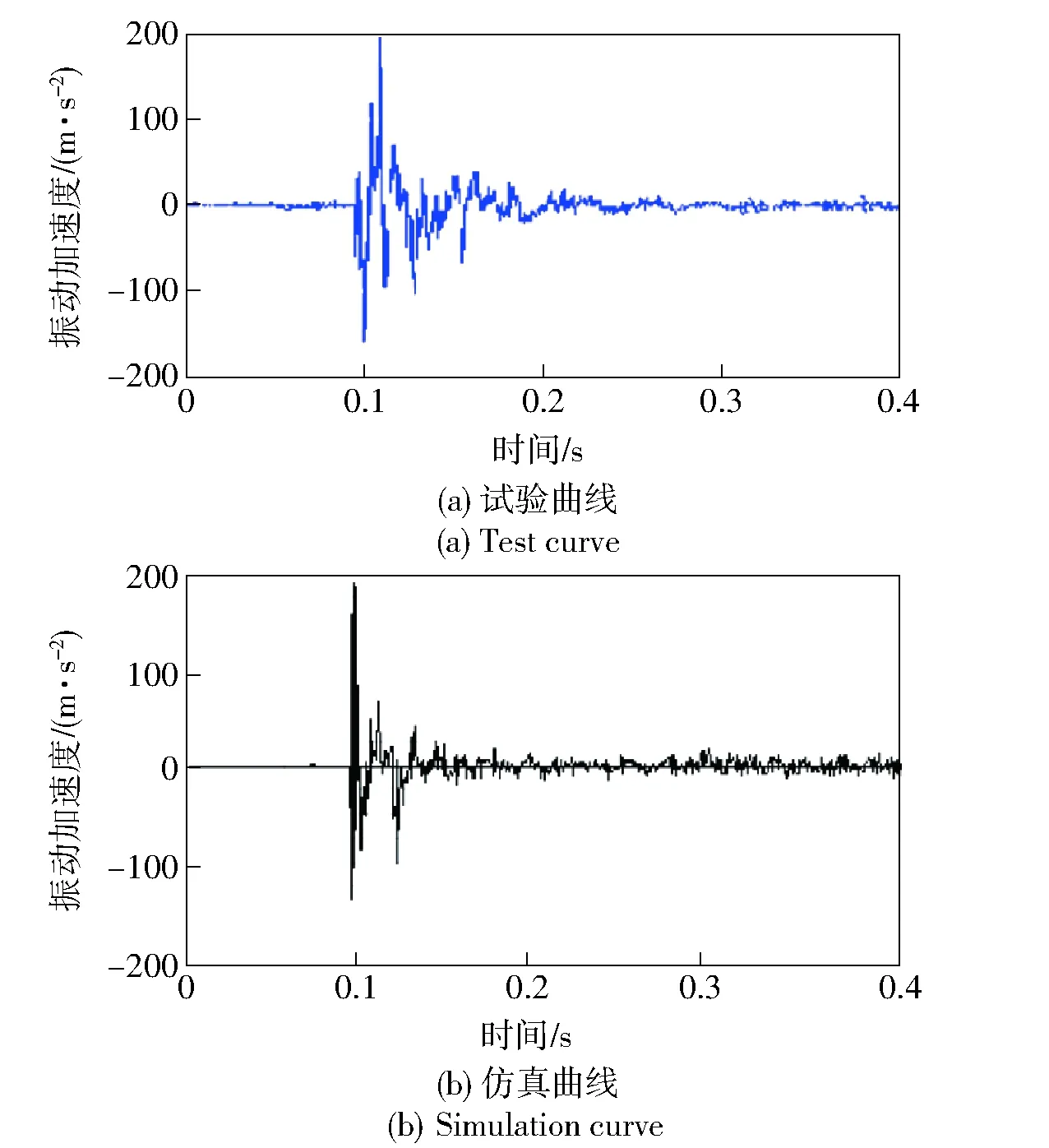
圖8　搖架左側高低向振動加速度隨時間變化曲線Fig.8　　　　Change of vibration acceleration on the left side of cradle over time

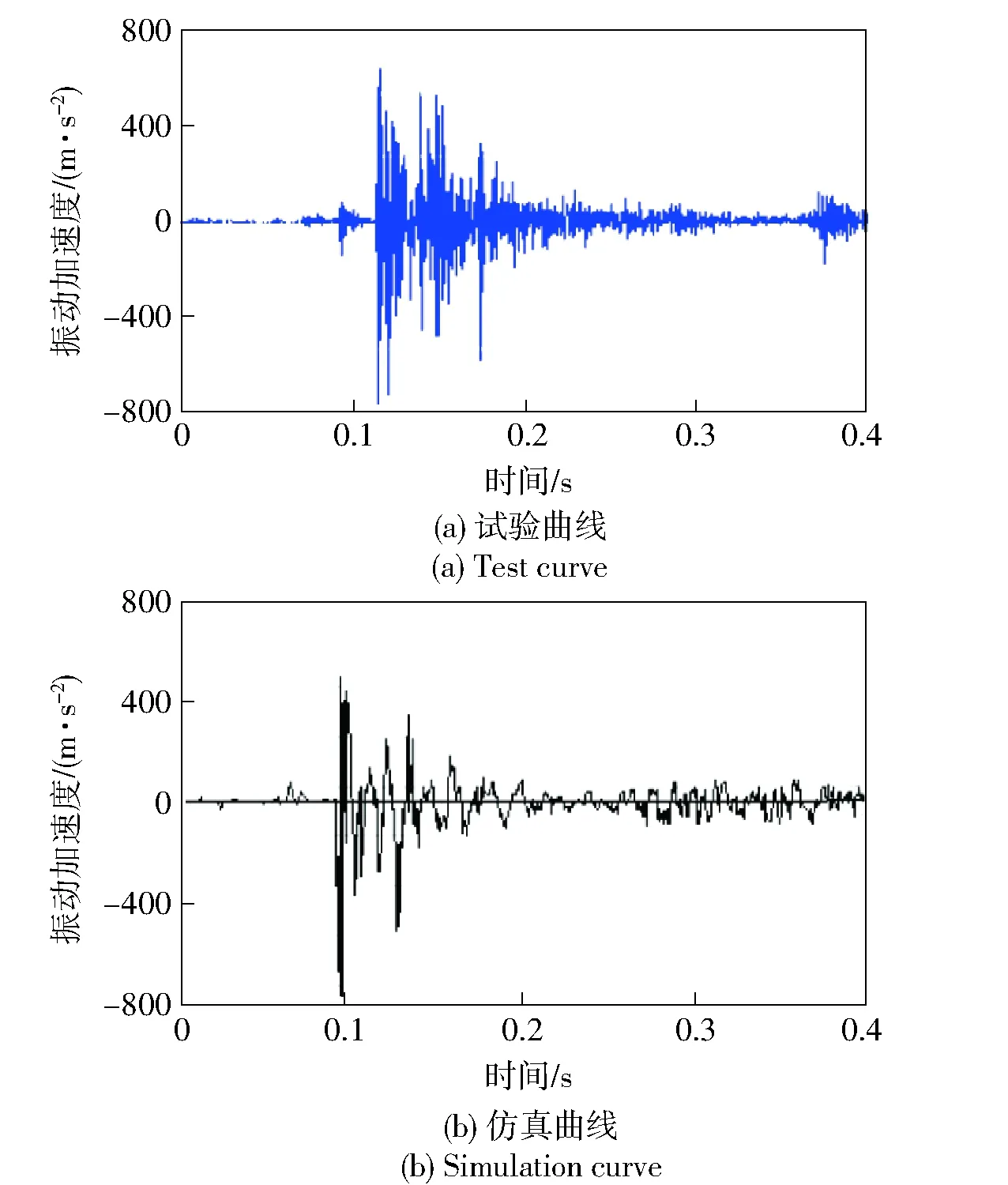
圖9　托架左前側高低向振動加速度隨時間變化曲線Fig.9　　　　Change of vibration acceleration on the left side of base structure over time

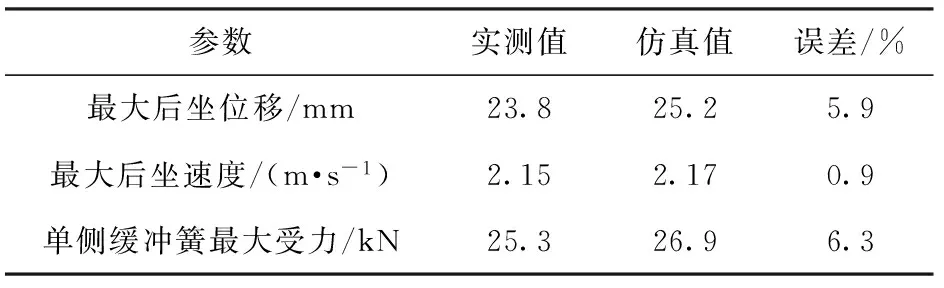
參數實測值仿真值誤差/%最大后坐位移/mm23.825.25.9最大后坐速度/(m·s-1)2.152.170.9單側緩沖簧最大受力/kN25.326.96.3

由圖8、圖9可知，射擊過程部件高低向振動加速度的試驗曲線與仿真曲線變化規律吻合較好，峰值相近，且由表1可知，最大后坐位移、最大后坐速度、單側緩沖簧最大受力等特征參數的試驗值與仿真值誤差小于10%，以上表明所建立的頂置武器站剛柔耦合動力學模型準確可靠，精度滿足工程分析要求。

2　基于Kriging模型的優化設計方法

Kriging模型由法國地質學家Krige提出，其本質上是一種基于統計理論的近似模型。由于Kriging可對原復雜動力學模型進行高度近似，同時通過一定方式擬合而成，具有結構簡單、計算量小的優點，可以大大縮短單次仿真時間。對于上述1.2節建立的頂置武器站剛柔耦合發射動力學模型，單次仿真耗時約為1.5 h，若采用該模型進行優化計算，迭代次數需要上千次，則優化總時間長達數月，顯然無法滿足武器站結構參數優化的高效仿真需求。因此，本文采用基于Kriging模型的優化設計方法對武器站結構參數進行優化。

2.1Kriging擬合機理

Kriging作為一種半參數化的近似模型，由線性回歸部分和非參數部分組成[12]：

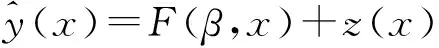
(9)

式中：F(β,x)為回歸部分，由一系列x的多項式及回歸系數β來共同決定：

F(β,x)=β1f1(x)+β2f2(x)+…+βnfn(x)=

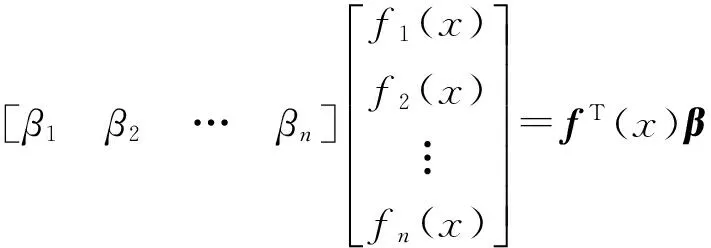
(10)

在插值過程中F(β,x)提供全局近似，且x的多項式形式可以選擇為0階、1階或2階。

z(x)為非參數部分，在插值過程中提供局部偏差的近似，具有以下統計特性：

(11)

式中：E為期望；Var(·)為方差；Cov(·)為協方差；R為相關函數；θ為相關向量。

2.2Kriging序列優化設計流程

Kriging序列優化方法首先選擇試驗設計方法對設計變量進行一定數量的采樣，通過原模型仿真得到響應值后構造初始訓練樣本空間；基于該樣本空間建立第一代Kriging模型，選擇優化算法對當前Kriging模型進行優化；當優化結果滿足收斂準則時，表明當前尋優結果為最終結果，當不滿足收斂準則時，需要通過加點準則確定待添加樣本點的位置，并通過原模型仿真得到響應值后納入原訓練樣本空間中，重新進行Kriging模型的構建及尋優。上述建模、優化步驟反復進行，直至優化結果滿足收斂準則為止。流程如圖10所示。

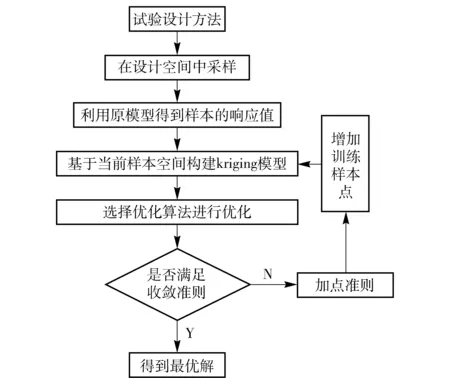
圖10　Kriging序列優化流程Fig.10　　　　Flow chart of Kriging sequential optimization method

2.3拉丁超立方試驗設計

拉丁超立方試驗設計[13]通過控制采樣點位置來避免小領域的重合問題。在確定樣本個數n后，拉丁超立方試驗設計將設計變量的取值范圍均勻劃分成n等分，然后在每個區間內隨機進行取值。以2設計變量為例，假設水平數為5，則樣本數也為5，經拉丁超立方試驗設計得到的采樣點分布如圖11所示。由于同一設計變量在每個區間有且只能取值一次，因此樣本點能夠有效分布在整個設計空間。

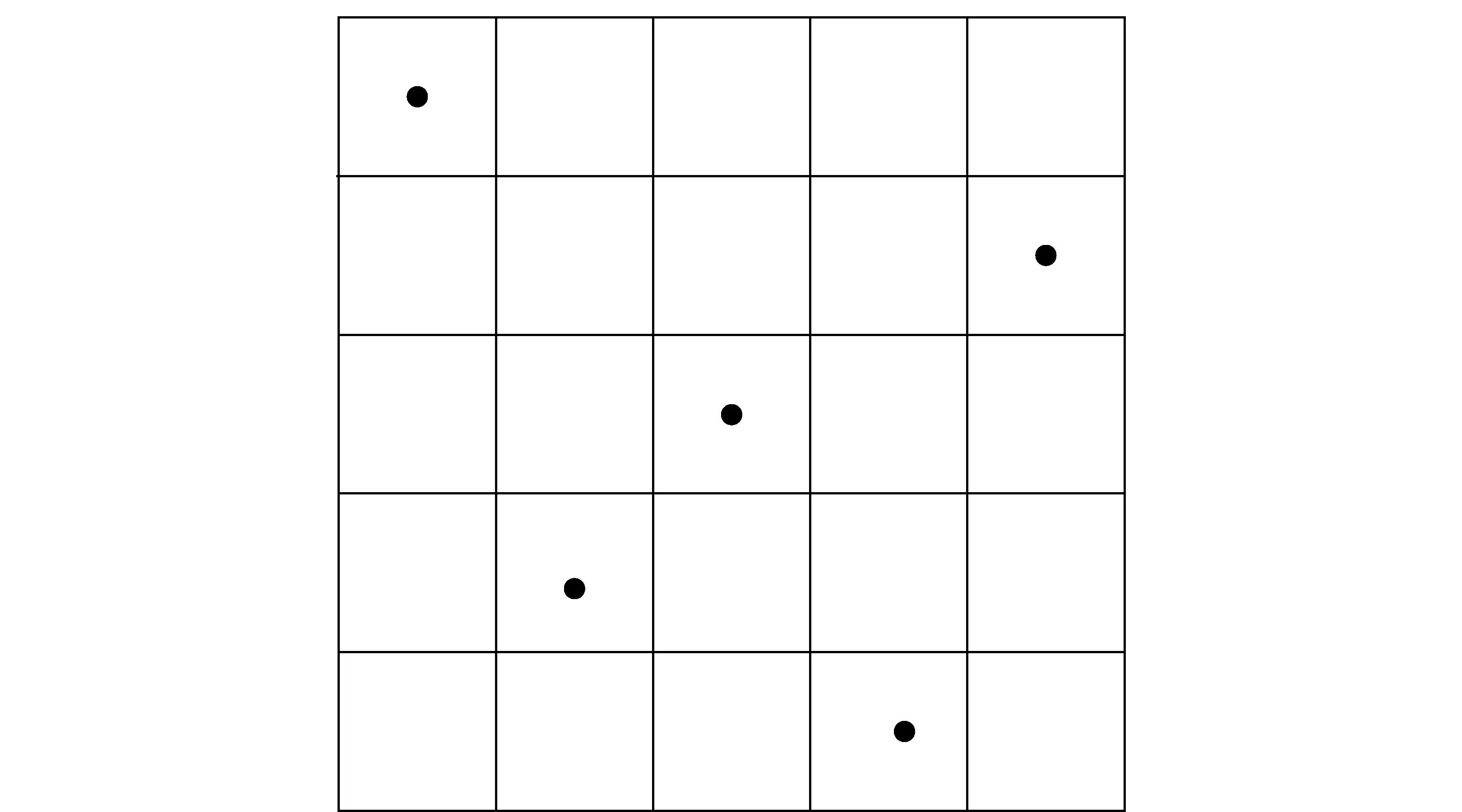
圖11　拉丁超立方設計采樣點分布Fig.11　Distribution of Latin hypercube sampling points

2.4遺傳算法

在遺傳算法中，優化問題的每個可行解相當于生物學個體，初始種群由N個個體隨機組成，當適應度函數確定后，每個個體的適應度得以確定，再從其中選擇適應度高的個體進行遺傳操作(包括選擇、交叉及變異)，產生下一代種群。如此反復進行，最終收斂到一個適應度最好的個體(即全局最優解)，其過程如圖12所示。

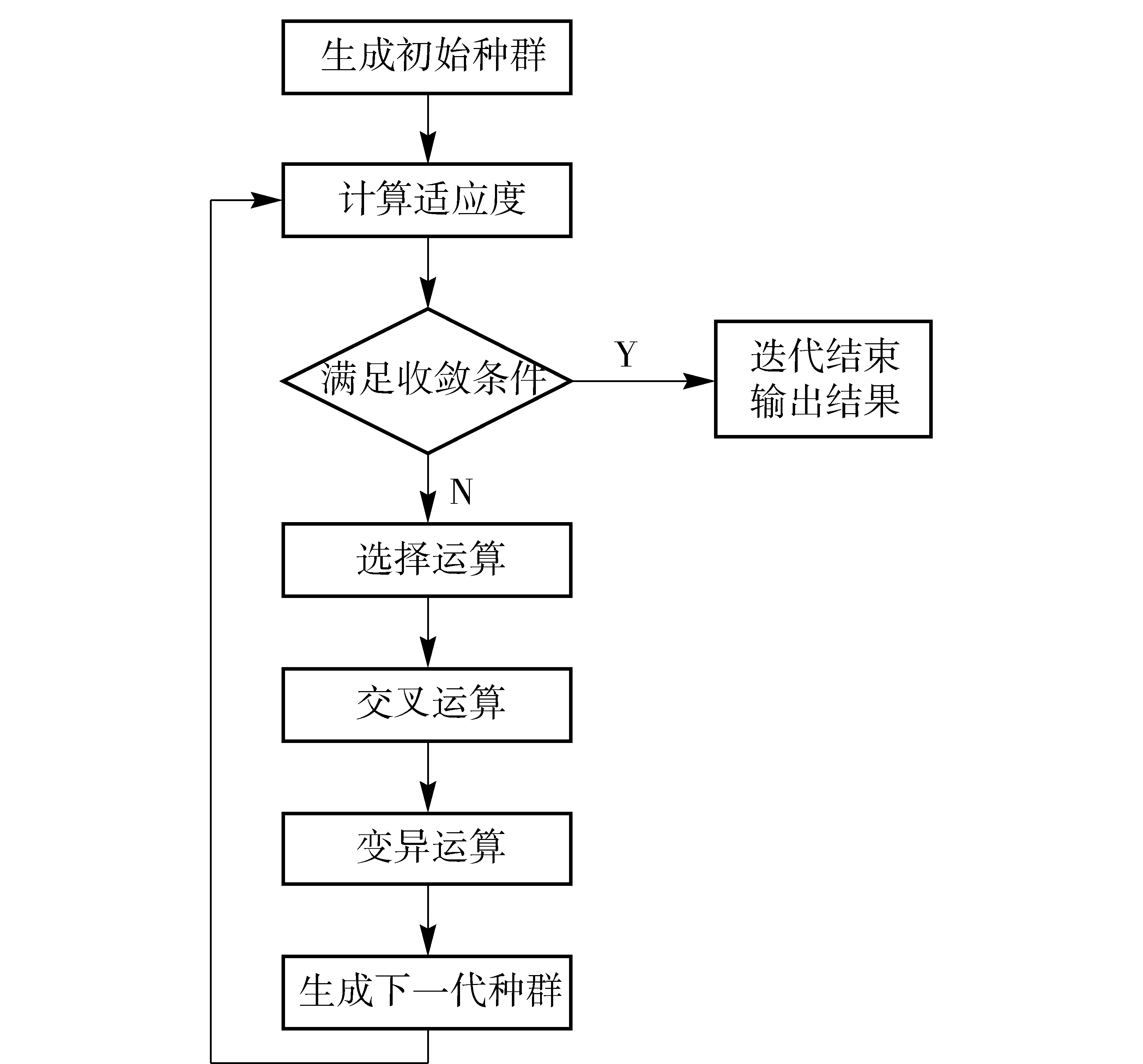
圖12　遺傳算法迭代流程Fig.12　Iterative process of genetic algorithm

2.5最大化期望提高加點準則

與一般數據擬合方法不同的是，基于Matlab/Dace工具箱構建的Kriging模型不僅可以對某一未知點進行預測，而且還提供了該點的預測標準差。該值反映了Kriging模型在該點附近的樣本稀疏性及不確定性，即預測標準差越小，不確定性越小、樣本越集中；預測標準差越大，不確定性越大、樣本越稀疏。基于上述特點，Schonlau等[14]提出了最大化期望提高的加點準則，被譽為是“有效的全局優化設計方法”。

假設M個設計變量、N個約束條件的最小化優化問題為

(12)

式中：f(x)為目標函數；li、ui分別為設計變量xi的取值下限、取值上限；gj為第j個約束條件。

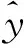
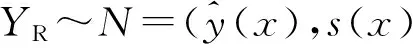
(13)

假設ymin為當前訓練樣本中的最小值：

ymin=min (y1,y2,…,yn) .

(14)

定義未知點x處響應值的提高為

I=ymin-YR.

(15)

隨機變量I同樣服從正態分布，相應的概率密度函數為

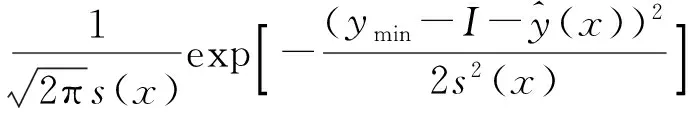
(16)

則響應值提高I的期望E(I)為

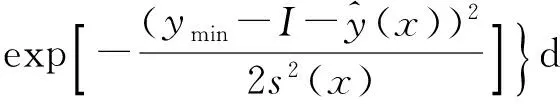
(17)

對(17)式進行分部積分可得

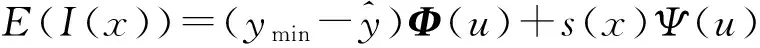
(18)

式中：Φ(·)、Ψ(·)分別為標準化的概率分布函數和概率密度函數。

3　基于Kriging模型的武器站炮口擾動優化

為了提高頂置武器站炮口擾動優化的仿真效率，采用Kriging序列優化方法對其進行優化。

3.1設計變量

考慮到緩沖器屬性及身管屬性對武器站炮口擾動有重要影響，因此選擇緩沖器阻尼C、身管彈性模量E及身管泊松比μ作為優化問題的設計變量，其取值范圍如表2所示。

表2　設計變量取值范圍

3.2目標函數

文獻[15]指出，炮口擾動的劇烈程度可由角位移和線速度進行表征，每種參量又分為高低向及水平向，即描述炮口擾動的表征量總共包括高低向角位移θe、高低向線速度ve、水平向角位移θh及水平向線速度vh. 此外，考慮到本文目的在于提高準確度以提高射擊精度，因此選擇上述擾動參量的最大振幅作為優化目標函數的組成元素，并通過線性加權構造一個炮口擾動綜合函數：

minZ=min (w1θe+w2ve+w3θh+w4vh)，

(19)

式中：w1、w2、w3、w4為權系數，作用是將不同參量的量綱進行統一，4個權系數取值為

(20)

3.3約束條件

根據頂置武器站性能及空間安裝等要求，確定以下約束關系：

1)應力約束：前支撐架最大等效應力σmmax≤350 MPa；托架最大等效應力σbmax≤350 MPa.

2)后坐約束：最大后坐位移l≤35 mm.

3.4初始訓練樣本空間

采用拉丁超立方試驗設計對緩沖器阻尼、身管彈性模量及泊松比等3個設計變量進行25個樣本點的采樣，利用頂置武器站動力學模型仿真得到炮口擾動各參量響應值，代入(19)式中計算炮口擾動綜合量。聯立設計變量及相應的綜合量生成初始訓練樣本空間，部分訓練樣本如表3所示。

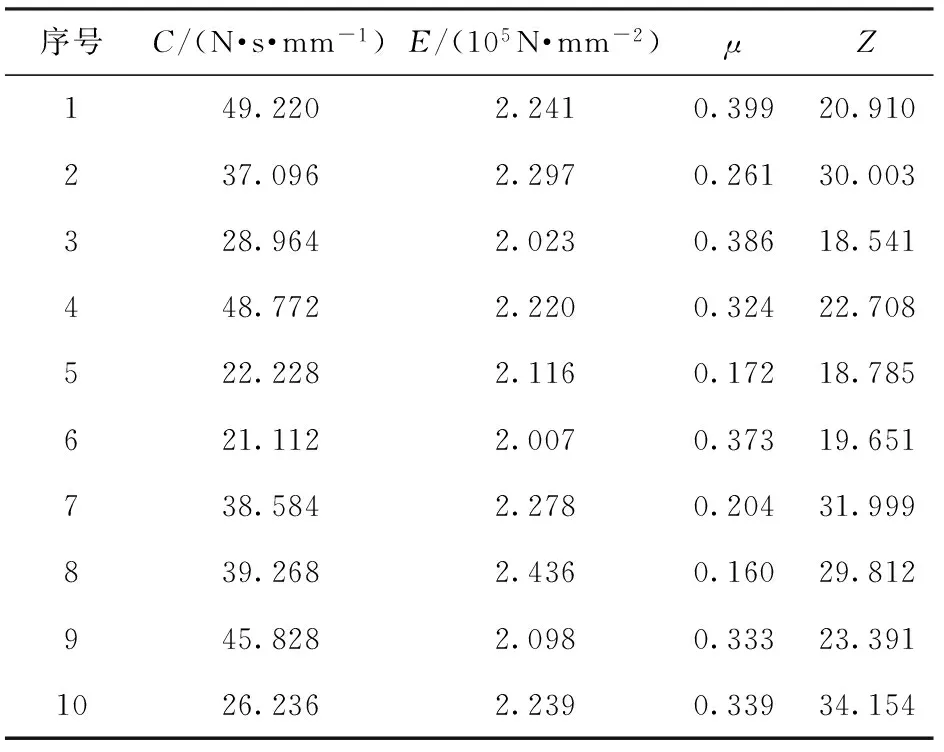
表3　初始訓練樣本空間

3.5優化參數

基于上述初始訓練樣本集，利用Matlab/DACE工具箱構造第一代Kriging模型，回歸函數選擇二元二次多項式，相關函數選擇高斯函數，考慮各向異性作用，每個設計變量單獨賦予θ值，范圍取[0.1,20]，初始值統一設置為10.

優化算法選擇遺傳算法，設置種群數量為44，交叉概率為0.7，變異概率為0.05，收斂閥值為0.001.

3.6優化結果與分析

依據上述初始條件，采用Kriging序列優化算法對武器站炮口擾動綜合函數進行優化，尋優結果如表4所示。

表4　炮口擾動綜合量尋優結果

整個優化過程經歷了34輪Kriging模型的更新，最終收斂的全局最優值為18.045，對應的設計變量為：緩沖器阻尼為51.68 N·s/mm，身管彈性模量為2.396×105N/mm2，身管泊松比為0.268 7. 相比初始值，優化值降低21.06%. 在特征點尋優過程中發現，最優值并不是一味地變小，而是在-300～-10間來回波動，這是由于擬合出的Kriging模型具有若干個相近的極小值點，當前Kriging模型的最優點經加點提高準確度后，另一個相近的極小值點凸顯出來，成為下一輪Kriging模型的最優點，如此反復尋優、加點，一直到該若干個極小值點被“填平”、全局最優點留存下來為止。

將優化參數代入頂置武器站剛柔耦合動力學模型進行仿真，以高低向振動參量為例，優化前后的對比如圖13、圖14、表5所示。

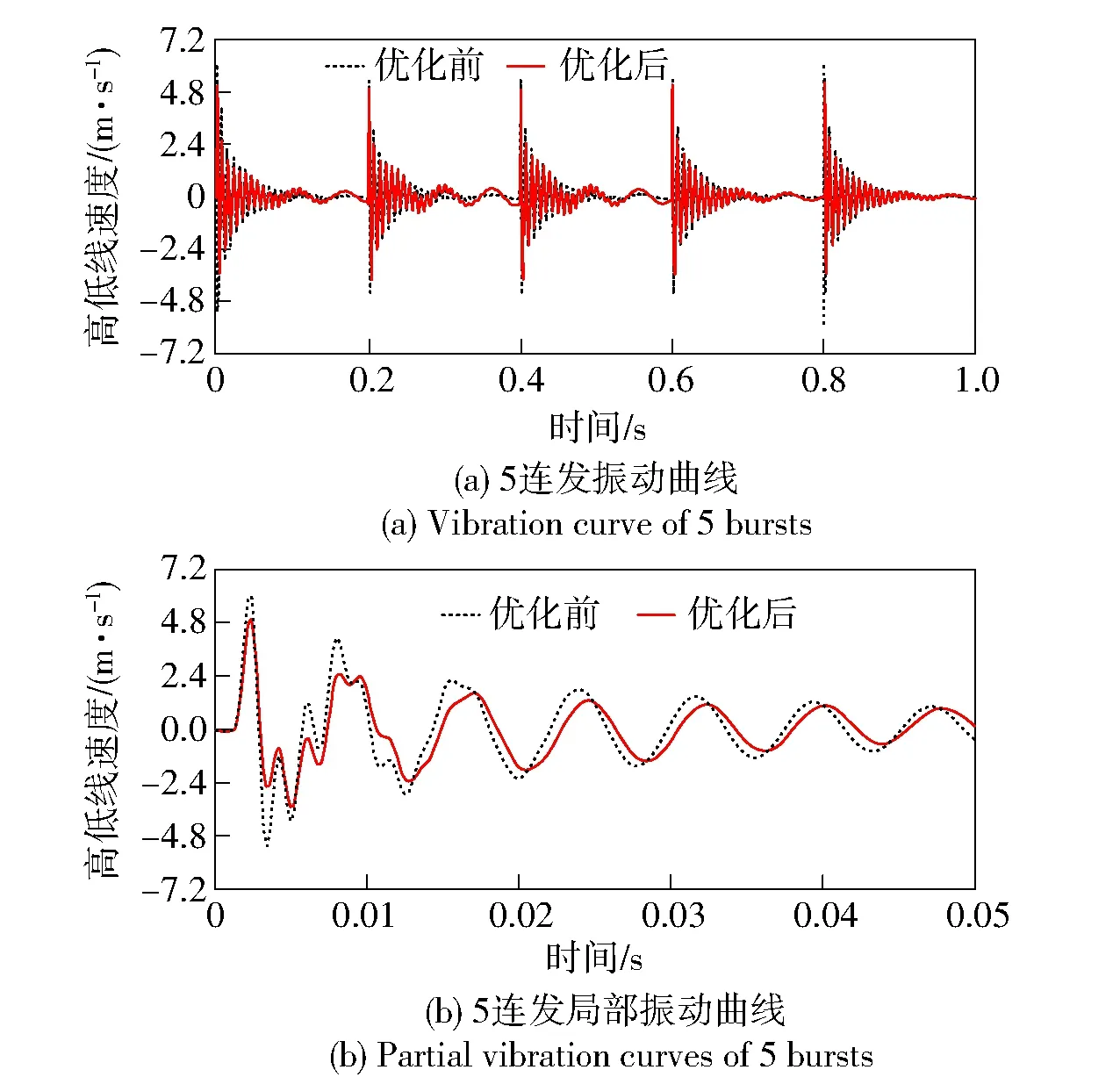
圖13　優化前后炮口擾動高低向線速度曲線Fig.13　　　　Comparison of muzzle disturbance vertical velocity curves before and after optimization

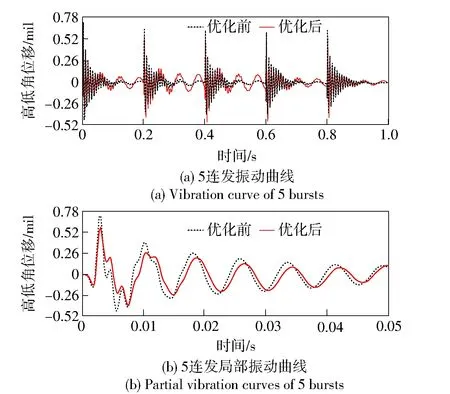
圖14　優化前后炮口擾動高低向角位移曲線Fig.14　　　　Comparison of muzzle disturbance elevation angle displacements before and after optimization

由優化前后仿真對比可知，優化后的炮口擾動參量最大振幅均有不同程度的改善，其中，高低向線速度、水平向線速度、高低向角位移、水平向角位移最大振幅分別降低14.74%、21.91%、20.12%、26.41%，優化效果顯著。

表5　優化前后炮口振動參量最大振幅對比

4　結論

本文以頂置武器站炮口擾動為研究對象，通過理論研究、仿真建模、試驗驗證等方法建立起武器站剛柔耦合動力學模型，并基于Kriging序列優化方法對其進行優化，主要有以下結論：

1)考慮部件柔性變形能使發射動力學模型更為符合客觀實際，且基于模態坐標建立的有限元模型能有效權衡模型精度和仿真效率之間的矛盾。

2)基于Kriging模型的序列優化算法，具有仿真高效性及廣泛適用性，尤其對于大規模、多峰值的復雜目標函數，該算法的優勢更為明顯。

3)通過對武器站緩沖器阻尼、身管彈性模量及身管泊松比等參數的優化，尋優結果能使射擊載荷引起的炮口擾動得到有效抑制。

References)

[1]毛保全. 車載武器技術概論[M]. 北京:國防工業出版社, 2009:22-23.

MAO Bao-quan. Firing introduction of vehicle mounted weapon[M]. Beijing:Natinal Defense Industry Press, 2009:22-23.(in Chinese)

[2]徐禮. 頂置武器站發射動力學仿真與結構參數優化研究[D]. 北京:裝甲兵工程學院, 2013.

XU Li. Study on launch dynamics simulation and structural parameters optimization for overhead weapon station[D]. Beijing:Academy of Armored Force Engineering, 2013.(in Chinese)

[3]田發達, 姚養無. 某型車載遙控武器站發射動力學仿真分析[J]. 計算機仿真, 2012, 29(2):15-18.

TIAN Fa-da, YAO Yang-wu. Launch dynamic simulation and analysis of certain vehicle remote control weapon station[J]. Computer Simulation, 2012, 29(2):15-18.(in Chinese)

[4]張海燕, 周潤強, 徐禮, 等. 遙控武器站結構參數對射擊密集度靈敏度影響分析[J]. 火炮發射與控制學報, 2013(4):54-58.

ZHANG Hai-yan, ZHOU Run-qiang, XU Li, et al. Influence of structure parameters of remote control weapon stations on sensitivity of firing intensity[J]. Journal of Gun Launch & Control, 2013(4):54-58.(in Chinese)

[5]梁傳建, 楊國來, 葛建立, 等. 反后坐裝置結構布置對炮口振動影響的研究[J]. 兵工學報, 2013, 34(10):1209-1214.

LIANG Chuan-jian, YANG Guo-lai, GE Jian-li, et al. Study on influence of structural arrangement of recoil mechanism on muzzle vibration of gun[J]. Acta Armamentarii, 2013, 34(10):1209-1214.(in Chinese)

[6]王紅, 王希誠, 李克秋. 混合Kriging代理模型的高維參數估計優化算法[J]. 大連理工大學學報, 2015,55(2):215-222.

WANG Hong, WANG Xi-cheng, LI Ke-qiu. Hybrid Kriging surrogate model optimization algorithm for high-dimension parameter estimation[J]. Journal of Dalian University of Technology, 2015,55(2):215-222.(in Chinese)

[7]王曉強, 羅娜, 葉貞成, 等. 基于Kriging的差分進化算法及其在苯乙烯流程優化中的應用[J]. 化工學報, 2013, 64(12):4563-4570.

WANG Xiao-qiang, LUO Na, YE Zhen-cheng, et al. Differential evolution algorithm based on Kriging and its application in styrene plant optimization[J]. CIESC Journal, 2013, 64(12):4563-4570.(in Chinese)

[8]周算, 強洪夫, 王學仁, 等. 基于Kriging代理模型的錐柱形膜片屈曲載荷計算[J]. 航空動力學報, 2014, 29(1):111-117.

ZHOU Suan, QIANG Hong-fu, WANG Xue-ren, et al. Buckling load computation of spherical-cone diaphragms based on Kriging metamodel[J]. Journal of Aerospace Power, 2014, 29(1):111-117.(in Chinese)

[9]何歡, 朱廣榮, 何成, 等. 基于Kriging模型的結構耐撞性優化[J]. 南京航空航天大學學報, 2014, 46(2):297-303.

HE Huan, ZHU Guang-rong, HE Cheng, et al. Crashworthiness optimization based on Kriging metamodeling[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(2):297-303.(in Chinese)

[10]鄧志平, 蔣水華, 曹子君, 等. 考慮參數空間變異性邊坡可靠度分析的Kriging方法[J]. 武漢大學學報:工學版,2014, 47(6):743-749.

DENG Zhi-ping, JIANG Shui-hua, CAO Zi-jun, et al. Reliability analysis of slope stability considering spatially varying soil properties using Kriging method[J]. Engineering Journal of Wuhan University, 2014, 47(6):743-749.(in Chinese)

[11]康新中, 吳三靈, 馬春茂, 等. 火炮系統動力學[M]. 北京:國防工業出版社, 1999:234-238.

KANG Xin-zhong, WU San-ling, MA Chun-mao, et al. Gun system dynamics[M]. Beijing:National Defense Industry Press, 1999:234-238.(in Chinese)

[12]朱茂桃, 錢洋, 顧婭欣, 等. 基于Kriging模型的車門剛度和模態優化[J]. 汽車工程, 2013, 35(11):1047-1050.

ZHU Mao-tao, QIAN Yang, GU Ya-xin, et al. Stiffness and modal optimization of car door based on Kriging model[J]. Automotive Engineering, 2013, 35(11):1047-1050.(in Chinese)

[13]張建平, 張立波, 程浩忠, 等. 基于改進拉丁超立方抽樣的概率潮流計算[J]. 華東電力, 2013, 41(10):2028-2034.

ZHANG Jian-ping, ZHANG Li-bo, CHENG Hao-zhong, et al. Evaluation of probabilistic load flow based on improved Latin hypercube sampling[J]. East China Electric Power, 2013, 41(10):2028-2034.(in Chinese)

[14]Schonlau M, Welch J, Jones D. Global versus local search in constrained optimization of computer models[C]∥New Developments and Applications in Experimental Design. Seattle, WA, US:Institute of Mathematical Statistics, 1998:11-25.

[15]吳永亮, 毛保全, 高玉水, 等. 基于立靶密集度的小口徑連發武器炮口振動參數控制模型[J]. 火炮發射與控制學報, 2013(3):6-9.

WU Yong-liang, MAO Bao-quan, GAO Yu-shui, et al. Small caliber automatic weapon muzzle vibration parameters control model based on vertical target density[J]. Journal of Gun Launch & Control, 2013(3):6-9.(in Chinese)

Optimization of Muzzle Disturbance of Overhead Weapon Station Based on Kriging Model

DENG Wei, MAO Bao-quan, FENG Shuai, LI Cheng

(Department of Arms Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

Muzzle disturbance is an important factor to affect the firing accuracy of overhead weapon station (OWS). In order to study the approach to inhibite the muzzle disturbance, an OWS rigid-flexible coupling dynamic model is established based on finite element theory, of which accuracy is verified by the firing accuracy test. The synthetic function of muzzle disturbance is defined as optimization objective to construct an optimization design model of OWS muzzle disturbance, and the Kriging sequential optimization method is used to solve the optimization problem. The simulated results show that the finite element model, considering the flexible deformation of parts , is a good approximation of the vibration characteristics of real system, and Kriging sequential optimization method can be applied to solve the optimization problems of OWS muzzle disturbance. The global optimal solutions searched in optimization problems can be used to suppress OWS muzzle disturbance.

ordnance science and technology; overhead weapon station; muzzle disturbance; finite element model; Kriging sequential optimization

2016-02-01

武器裝備預先研究項目(2011YY34)

鄧威(1986—)，男，博士研究生。E-mail: 314829483@qq.com；

毛保全(1965—)，男，教授，博士生導師。E-mail:mbq_1965@sina.com

TJ301

A

1000-1093(2016)10-1795-08

10.3969/j.issn.1000-1093.2016.10.005