兩種量熱模式下物質熱分解的動力學補償效應

尹瑞麗　陳利平,*　陳網樺　吳　珂張彩星　李　焓　于　誠

(1南京理工大學化工學院安全工程系，南京210094；2常州出入境檢驗檢疫局，江蘇常州213003)

兩種量熱模式下物質熱分解的動力學補償效應

尹瑞麗1陳利平1,*陳網樺1吳珂2張彩星1李焓1于誠1

(1南京理工大學化工學院安全工程系，南京210094；2常州出入境檢驗檢疫局，江蘇常州213003)

熱分析量熱儀主要包括動態、等溫、恒溫及絕熱四種操作模式。很多學者基于動態及等溫模式的測試結果，采用Arrhenius速率常數進行動力學計算，進而發現了所謂的“動力學補償效應”。為了解絕熱模式下是否也存在動力學補償效應，分別采用絕熱加速量熱法(ARC)及動態差示掃描量熱法(DSC)研究了過氧化二異丙苯(DCP)、40%(質量分數，下同)DCP溶液、葡萄糖、45%葡萄糖溶液的熱分解特性，在此基礎上基于Arrhenius公式計算了對應的表觀活化能E和指前因子A，并對計算結果進行了分析。結果表明：絕熱模式下，不同質量的同種樣品及其溶液的最佳動力學參數，或者同一組數據采用不同的反應級數獲得的lnA和E之間均存在明顯的線性關系。此外，盡管由動態DSC數據計算獲得的E和lnA普遍小于絕熱模式的結果，但兩種模式下獲得的lnA和E之間仍然存在動力學補償效應。由此可以推斷，具有相同或類似反應機理的反應，雖然實驗模式不同，但其E和lnA之間存在明顯的動力學補償效應。

動力學補償效應；絕熱模式；動態模式；活化能；指前因子

doi:10.3866/PKU.WHXB201511023

1　引言

熱分析及量熱方法在科學研究和生產實踐中的應用越來越廣泛，其主要研究物質(料)在各種熱環境下發生各種物理、化學變化的過程1。求解描述某反應的“動力學三因子”(表觀活化能E、指前因子A和反應機理函數f(α))是熱分析動力學研究的目的2。而求解E和A常用Arrhenius公式3,4：

上式中T為開氏溫度；R為氣體常數；k為反應速率常數。

理論上，動力學三因子應該是相互獨立的變量。然而，1976年，Gallagherh和Johnson5首先在Cu催化C2H5OH脫水反應中發現了所謂的動力學補償效應(kinetic compensation effect)，即lnA與E呈線性關系的現象，表達式為：

上式中a和b為補償參數，a的單位2是mol?kJ－1。

隨后，更多學者發現了類似的現象，如張冬梅6、Qin7、Pouretedal8等對動態模式的熱分析數據進行動力學計算，發現了lnA與E的線性關系；Pouretedal等還進一步根據lnA與E的線性關系預測了A的值。陳鴻偉等9則基于等溫模式的測試結果發現了該現象。同時，還有學者嘗試從樣品與反應過程的物理化學性質，實驗的各種因素和動力學計算的數學結果等方面對這種現象進行探討10－15。文獻16指出動力學補償效應的存在是Arrehnius速率常數指數形式的必然結果，并利用數學方法進行了證明。

盡管已有報道對動力學補償效應進行研究，然而這些研究都是基于動態模式(線性升溫)或等溫模式下的實驗數據而開展的。實際上，動力學分析在絕熱測試與分析中同樣需要，但目前尚無這方面的報道。

過氧化二異丙苯(DCP)受熱易分解，其分解熱非常大，采用較小的樣品量，最大溫升速率就會超過ARC的跟蹤速率。為了降低DCP的反應熱，同時選用質量分數為40%的DCP的乙苯溶液(40% DCP)進行研究。乙苯在測試溫度范圍內不參加反應。因此，理論上DCP和40%DCP的動力學參數必然有相關之處。

為了研究不同分解機理的樣品，獲得的動力學參數是否有顯著不同，選擇分解機理與DCP不同的葡萄糖和45%葡萄糖水溶液進行測試。

因此本文利用絕熱加速量熱儀(ARC)對以上4種樣品進行絕熱測試及動力學計算，進而將結果與差示掃描量熱法(DSC)動態模式下的動力學參數進行比較，探討兩種模式下的動力學補償效應。

2　試劑和實驗條件

2.1試劑

過氧化二異丙苯，99.5%(w，質量分數,下同)，阿拉丁試劑；乙苯，98.5%，國藥集團化學試劑有限公司；葡萄糖(D-(+)-Glucose)，大于99.5%，阿拉丁試劑。

待測樣品為：DCP，40%DCP的乙苯溶液(40%DCP)，葡萄糖，45%的葡萄糖水溶液(45%葡萄糖)。

2.2實驗設備和測試條件

ARC：英國Thermal Hazard Technology公司生產的絕熱加速量熱儀(esARC)。

ARC測試條件：加熱-等待-搜索模式，溫升臺階5°C，檢測靈敏度0.02°C?min－1，等待時間10 min，樣品球為鈦球，比熱容0.53 J?g－1?K－1。

絕熱模式測試時，樣品釋放的熱量有一部分不可避免地用來加熱樣品池，從而導致所測溫度曲線也受其影響。因此需要采用熱修正系數Ф進行修正17－20，熱修正系數定義為：

對測得的絕熱溫升進行修正，得到：

由此得到樣品的比放熱量為：

式中，mcell為樣品球的質量，g；Cpcell為樣品球的比熱，J?g－1?K－1；ms為樣品質量，g；Cps為樣品的比熱，J?g－1?K－1；ΔT為實測絕熱溫升，°C；ΔTad為修正后的絕熱溫升，°C；H為修正后的比放熱量，J?g－1。

ARC測試中，4種樣品的質量和對應的Ф值列于表1。

表1　ARC測試的樣品質量及Ф值Table 1　Sample masses and Φ values inARC tests

DSC測試采用瑞士Mettler Toledo公司生產的DSC-1。DSC測試條件：DCP和40%DCP溶液的測試溫升速率β分別為2、4、8、10 K?min－1。樣品質量如表2所示。葡萄糖和45%葡萄糖溶液的測試溫升速率分別為1、4、8、10 K?min－1，升溫速率差別越大，得到樣品的起始分解溫度和峰溫差別越大，求取活化能和指前因子時，數據擬合范圍越寬，所以在對葡萄糖及其溶液測試時，升溫速率改為1 K?min－1。樣品質量如表3所示。

表2　DCP和40%DCP溶液的DSC測試質量Table2 MassesofDCPand40%DCPsolutioninDSCtests

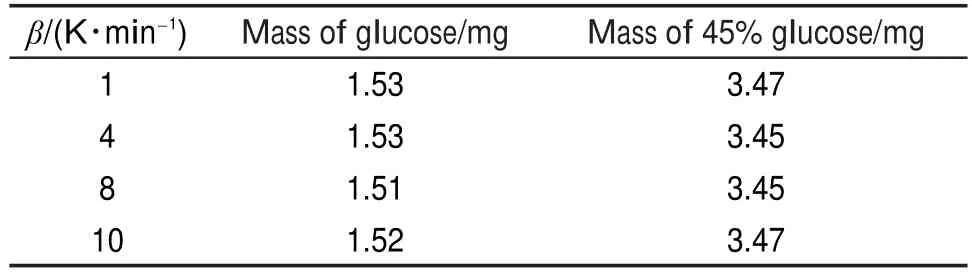
表3　葡萄糖和45%葡萄糖溶液的DSC測試質量Table 3　Masses of glucose and 45%glucose solutionin DSC tests

3　測試結果與討論

3.1測試結果

3.1.1ARC絕熱模式測試結果

表4和表5列出4種樣品ARC的測試結果，包括樣品起始分解溫度To，°C；修正后的絕熱溫升ΔTad，°C；最大放熱速率(dT/dt)m，°C?min－1；修正后的放熱量H，J?g－1等參數。

由ARC測試結果可知，Ф值不同，樣品球吸收的熱量所占樣品釋放熱量的比例不同，其溫度和溫升速率都是經過樣品球吸熱并經熱量平衡后的結果。實測得到的起始分解溫度、絕熱溫升、最大溫升速率等均具有明顯的差異。而對ARC數據進行動力學計算時，需要用到實測絕熱溫升和溫升速率等參數，由于這些參數的差異，動力學計算結果必然不同。

3.1.2DSC動態模式測試結果

圖1為4種樣品的DSC測試結果。結果顯示，溫升速率越大，對應的起始分解溫度和峰溫越高。DCP和葡萄糖的DSC曲線能觀察到明顯的熔化吸熱峰(峰向下)，它們的溶液則不存在吸熱峰。同時也可以發現，DCP與其溶液放熱峰的峰型，起始溫度等參數都比較接近，同樣的現象也能在葡萄糖及其溶液中觀察得到，其原因是作為溶劑的乙苯和水在測試的溫度范圍中很穩定，不參與反應。

3.2動力學計算

3.2.1基于絕熱模式數據的動力學計算

絕熱分解反應溫度與溫升速率的關系為:

令：

對(8)式兩邊取對數得：

式中dT/dt為溫升速率，°C?min－1；Tf為分解終止溫度，K；T為溫度，K；c0為反應物初始摩爾濃度，mol?L－1；n為反應級數17,21－23。

表4　DCP和40%DCP溶液的ARC測試結果Table 4　ARC test results of DCPand 40%DCPsolution

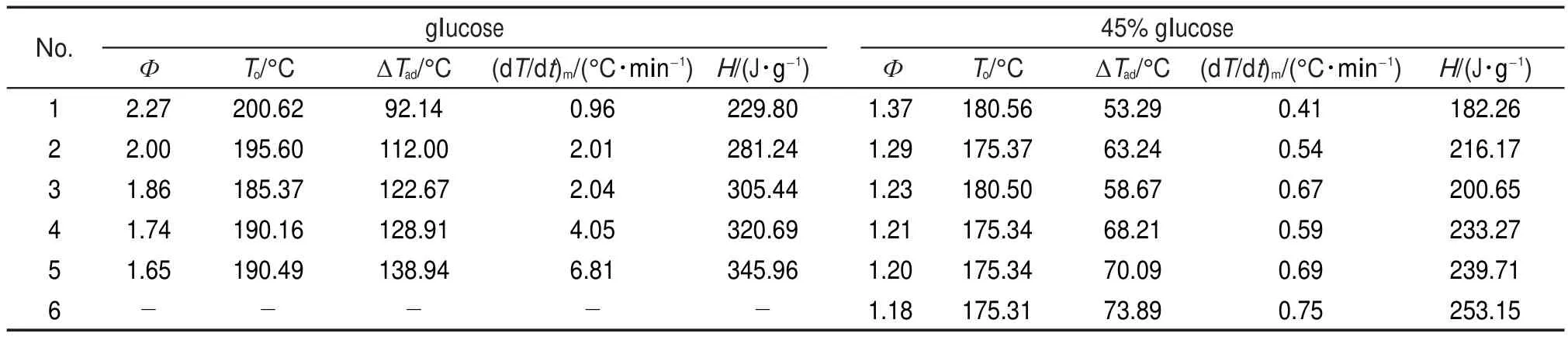
表5　葡萄糖和45%葡萄糖溶液的ARC測試結果Table 5　ARC test results of glucose and 45%glucose solution

圖1　4種樣品DSC的測試結果Fig.1　DSC test results of the four samples TS:sample temperature

選擇合適的反應級數n，使方程(9)中lnk*與1/T的關系為直線。利用Origin軟件進行擬合，由直線的斜率得到E，截距得到A。

采用上述方法對不同質量和Ф值的4種樣品進行動力學計算，并將相關系數最高的計算結果列于表6和表7。

表6　DCP和40%DCP溶液的lnA與E的計算結果Table 6　Calculated results of lnAand E for DCPand 40%DCPsolution

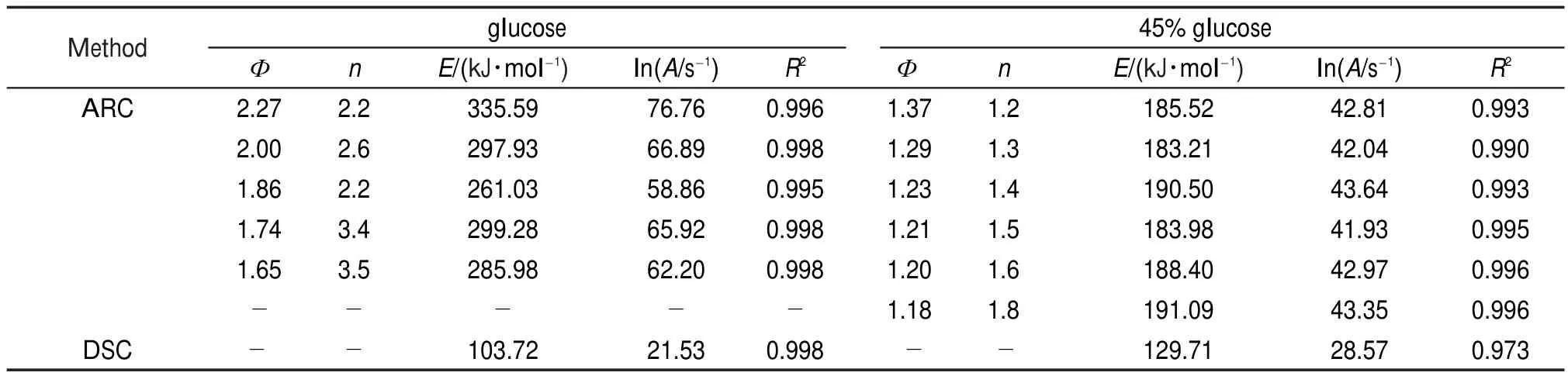
表7　葡萄糖和45%葡萄糖溶液的lnA與E的計算結果Table 7　Calculated results of lnAand E for glucose and 45%glucose solution

由表6和表7可知，基于絕熱模式數據計算lnA和E時，相關系數較高，說明選擇的n是可靠的。同時可以發現，如上文所述的現象，即不同Ф下的相同樣品，由于實測起始分解溫度，絕熱溫升等參數不同，計算得到的動力學參數也不同。由于進行動力學計算時所用的數據為實測參數，因此基于不同Ф下計算得到的動力學參數，實際上描述的是該Ф下的反應速率與溫度的關系，而不是該樣品本身絕熱分解的反應速率。

3.2.2基于動態模式數據的動力學計算

采用Kissinger方法24,25計算4種樣品峰溫處的E和lnA，其計算方法見式(10)：上式中i對應不同的溫升速率，Tpi為DSC測試的峰溫，K；βi為溫升速率，K?min－1。由對作圖，便可得到一條直線，從直線斜率求E，截距求lnA。計算結果同樣列于表6和表7中。

3.3動力學補償效應

3.3.1絕熱模式

為了考察在絕熱模式中動力學結果是否存在動力學補償效應。圖2給出了DCP和40%DCP溶液以及葡萄糖和45%葡萄糖溶液lnA和E的擬合曲線。圖2顯示溶于溶劑的樣品絕熱動力學結果和不含溶劑樣品結果之間存在良好的線性關系，即不論是否含有溶劑，絕熱模式下不同樣品質量的絕熱動力學參數E和lnA之間都存在良好的線性關系，即存在明顯的動力學補償效應。

此外，由表6和圖2(a)可知，同一種樣品在樣品量不同時，相同n值得到的lnA和E之間具有較好的線性關系。然而表7和圖2(b)顯示不同樣品量的實驗，即使在不同反應級數n下得到的lnA和E之間也具有較好的線性關系。為了探索這種現象存在的原因，這里以40%DCP溶液，質量為1.005 g的實驗數據為例，采用不同反應級數n對該測試結果進行處理，得到lnk*與1/T的關系(見圖3)，進而利用式(9)擬合得到不同反應級數下的lnA和E，擬合結果見表8。

將不同n下的lnA和E列于圖4。顯然，對同一組ARC數據，選用不同的反應級數n，得到的動力學參數之間存在明顯的動力學補償效應，并且其斜率(0.297)與圖2(a)的斜率(0.306)幾乎相等。這也是對同一樣品不同樣品質量的測試結果進行動力學計算時，盡管反應級數n值不同，lnA和E仍然存在良好線性關系的原因。

圖2　在ARC數據基礎上lnA和E的擬合結果Fig.2　Fitting results of lnAand E based onARC data

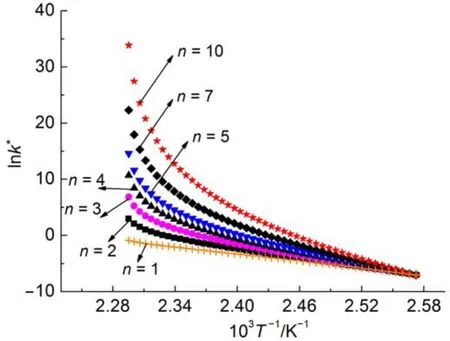
圖3　同一組數據不同n計算得到的lnk*與1/T的關系Fig.3　Relationship between lnk*and 1/T with different n for the same set of data k*:pseudo rate constant

表8　同一組數據不同n計算得到lnA和E的值Table 8　Calculated lnAand E with different n for the same set of data

圖4　同一組數據不同n計算得到的lnA和E的擬合結果Fig.4　Fitting results of lnAand E with different n for the same set of data

嘗試將DCP、葡萄糖、40%DCP和45%葡萄糖溶液的動力學結果共同列于圖5中，結果發現DCP和葡萄糖之間不存在動力學補償效應(見圖5)。而有關文獻表明，性質相近的物質相同實驗條件下進行同類型反應時，得到的動力學參數也具有明顯的動力學補償效應2。對比這兩種截然不同的結果可知：具有相同或者相似的反應機理才會存在動力學補償效應。

圖5　在ARC數據基礎上4種樣品的lnA和E擬合結果Fig.5　Fitting results of lnAand E for four samples based onARC data

3.3.2絕熱模式和動態模式結果

DSC的動態模式與ARC的絕熱模式測試原理以及動力學參數的處理過程均不同。為了研究分別基于動態模式和絕熱模式得到動力學處理結果之間是否同樣存在動力學補償效應，圖6給出了DCP和40%DCP溶液，葡萄糖和45%葡萄糖溶液在動態模式和絕熱模式測試基礎上獲得的E和lnA的關系。

圖6　在ARC和DSC數據基礎上lnA和E的擬合結果Fig.6　Fitting results of lnAand E based on ARC and DSC data

結果顯示，基于動態模式計算獲得的E和lnA普遍小于基于絕熱模式得到的結果，但是兩者之間存在良好的動力學補償效應。這從另一角度說明盡管測試模式不同，但是兩類樣品(DCP及其溶液，葡萄糖及其溶液)的反應機理并沒有發生變化。

4　結論

采用ARC和DSC兩種量熱設備獲得了4種樣品(DCP、40%DCP溶液、葡萄糖、45%葡萄糖溶液)在絕熱模式和動態模式下的熱分解特性，進而計算得到活化能E和指前因子A。結果如下：

(1)絕熱測試的樣品量不同會導致起始分解溫度、絕熱溫升等參數有所不同，但基于絕熱模式計算得到DCP和40%DCP溶液之間，葡萄糖和45%葡萄糖溶液之間存在明顯的動力學補償效應。

(2)盡管絕熱模式和動態模式的測試原理不同，且由動態模式獲得的E和lnA普遍小于絕熱模式的相應結果，但兩種模式下相同樣品及其溶液的lnA和E之間存在顯著的動力學補償效應。

(3)對絕熱測得的數據采用不同反應級數n進行動力學分析時，得到的lnA和E之間也會存在動力學補償效應。

(4)盡管操作模式不同，但是具有相同或相似反應機理的反應活化能和指前因子之間仍然會存在動力學補償效應。

References

(1)Chen,J.H.;Li,C.R.Thermal Analysis and Its Application, 1th ed.;Science Press:Beijing,1985;pp 6－118.[陳鏡泓,李傳儒.熱分析及其作用.第一版.北京:科學出版社,1985:6－118]

(2)Hu,R.Z.;Gao,S.L.;Zhao,F.Q.;Shi,Q.Z.;Zhang,T.L.; Zhang,J.J.Thermal Analysis Kinetics,2nd ed.;Science Press: Beijing,2008;pp 151－155.[胡榮祖,高勝利,趙鳳起,史啟禎,張同來,張建軍.熱分析動力學.第二版.北京:科學出版社,2008:151－155.]

(3)Tang,H.;Yan,Y.D.;Zhang,M.L.;Xue,Y.;Zhang,Z.J.;Du, W.C.;He,H.Acta Phys.-Chim.Sin.2013,29(8),1698.[唐浩,顏永得,張密林,薛云,張志儉,杜衛超,何輝.物理化學學報,2013,29(8),1698.]doi:10.3866/PKU. WHXB201305102

(4)Su,H.Z.;Yin,J.M.;Liu,Q.S.;Li,C.P.Acta Phys.-Chim. Sin.2015,31(8),1468.[宿洪禎,尹靜梅,劉青山,李長平.物理化學學報,2015,31(8),1468.]doi:10.3866/PKU. WHXB201506111

(5)Gallagher,P.K.;Johnson,D.W.Thermochim.Acta 1976,14 (3),255.doi:10.1016/0040-6031(76)85002-2

(6)Zhang,D.M.;Zheng,C.M.;Heng,S.Y.;Liu,Z.R.;Pan,Q.; Lu,H.L.Chinese Journal of Explosives&Propellants 2014, 37(3),82.[張冬梅,鄭朝民,衡淑云,劉子如,潘清,陸洪林.火炸藥學報,2014,37(3),82.]

(7)Qin,Z.;Balasubramanian,S.K.;Wolkers,W.F.;Pearce,J.A.; Bischof,J.C.Annals of Biomedical Engineering 2014,42(12), 2392.doi:10.1007/s10439-014-1100-y

(8)Pouretedal,H.R.;Ravanbod,M.J.Therm.Anal.Calorim. 2015,119(3),2281.doi:10.1007/s10973-014-4330-1

(9)Chen,H.W.;Chen,J.T.;Wei,R.G.;Chen,L.Journal of Central South University:JCR-SC 2013,44(4),1695.[陳鴻偉,陳江濤,危日光,陳龍.中南大學學報:自然科學版, 2013,44(4),1695.]

(10)Barrie,P.J.Phys.Chem.Chem.Phys.2012,14(1),318.doi: 10.1039/C1CP22666E

(11)Yelon,A.;Sacher,E.;Linert,W.Phys.Chem.Chem.Phys. 2012,14(22),8232.doi:10.1039/c2cp40618g

(12)Zuniga-Hansen,N.;Silbert,L.E.;Calbi,M.M.Breakdown ofKinetic Compensation Effect in Physical Desorption.http:// arxiv.org/abs/1503.06362(accessed Mar 21,2015).

(13)Garn,P.D.Therm.Anal.1976,10(1),99.doi:10.1007/ BF02179195

(14)Brill,T.B.;Gongwer,P.E.;Williams,G.K.J.Chem.Phys. 1994,98(47),12242.

(15)Liu,T.T.;Ran,Y.Y.;Wang,B.C.;Dong,W.B.;Wu,S.G.; Gong,J.B.Front.Chem.Sci.Eng.2014,8(1),55.

(16)Koga,N.;?esták,J.Thermochim.Acta 1991,182(2),201.doi: 10.1016/0040-6031(91)80005-4

(17)Townsend,D.I.;Tou,J.C.Thermochim.Acta 1980,37(1),1. doi:10.1016/0040-6031(80)85001-5

(18)Stoessel,F.Thermal Safety of Chemical Process:Risk Assessment and Process Design;Science Press:Beijing,2009; pp 73－74;translated by Chen,W.H.,Peng,J.H.,Chen,L.P. [Stoessel,F.化工工藝熱安全:風險評估與工藝設計.陳網樺,彭金華,陳利平,譯.北京:科學出版社,2009:73－74.]

(19)Lu,K.The Influence of the TypicalAdditives of Emulsion Explosives on the Thermal Decomposition of Emulsion Explosives.M.S.Dissertation,Nanjing University of Science and Technology,Nanjing,2009.[魯凱.乳化炸藥中典型組分對其熱分解行為影響的研究[D].南京:南京理工大學, 2009.]

(20)Fisher,H.G.;Forrest,H.S.;Grossel,S.S.;Huff,J.E.;Muller, A.R.;Noronha,J.A.;Shaw,D.A.;Tilley,B.J.Emergency Relief System Design Using DIERS Technology:The Design Institute for Emergency Relief Systems(DIERS)Project Manual;John Wiley&Sons:New York,2010:pp 385－395.

(21)Liu,R.H.;Chen,W.H.;Hu,Y.T.Safety Principle and Dangerous Chemicals Assessment Technology,1st ed.; Chemical Industry Press:Beijing,2004;pp 158－163.[劉榮海,陳網樺,胡毅亭.安全原理與危險化學品測評技術.第一版.北京:化學工業出版社,2004:158－163.]

(22)Chen,L.P.Experimental and Theoretical Studies on Thermal Hazards of Toluene Nitrations.Ph.D.Dissertation,Nanjing University of Science and Technology,Nanjing,2009.[陳利平.甲苯硝化反應熱危險性的實驗與理論研究[D].南京:南京理工大學,2009.]

(23)Zhou,Y.S.;Chen,L.P.;Chen,W.H.;Yang,T.;Zhang,C.X.; Yin,R.L.CIESC Journal 2014,65(11),4383.[周奕杉,陳利平,陳網樺,楊庭,張彩星,尹瑞麗.化工學報,2014,65 (11),4383.]

(24)Kissinger,H.E.Anal.Chem.1957,29(11),1702.doi:10.1021/ ac60131a045

(25)Peng,M.J.;Lu,G.B.;Chen,W.H.;Chen,L.P.;Lü,J.Y.Acta Phys.-Chim.Sin.2013,29(10),2095.[彭敏君,路貴斌,陳網樺,陳利平,呂家育.物理化學學報,2013,29(10),2095.] doi:10.3866/PKU.WHXB201307122

Kinetic Compensation Effect under Two Different Calorimetric Modes for Thermal Decomposition

YIN Rui-Li1CHEN Li-Ping1,*CHEN Wang-Hua1WU Ke2ZHANG Cai-Xing1LI Han1YU Cheng1
(1Department of Safety Engineering,School of Chemical Engineering,Nanjing University of Science and Technology,Nanjing 210094, P.R.China;2ChangzhouEntry-ExitInspectionandQuarantineBureau,Changzhou 213003,JiangsuProvince,P.R.China)

Thermal analysis calorimeters can be used with different temperature control modes.Dynamic, isothermal,isoperibolic,and adiabatic modes are commonly used.A kinetic compensation effect was discovered when the kinetic parameters were calculated using the Arrhenius equation,based on dynamic and isothermal data.To determine whether the kinetic compensation effect existed in adiabatic mode, accelerating rate calorimetry(ARC)and differential scanning calorimetry(DSC)were used to obtain thermal decomposition curves of dicumyl peroxide(DCP),40%(w)DCP in ethylbenzene,glucose,and 45% (w)glucose in water.The apparent activation energies(E)and pre-exponential factors(A)were calculated based on the Arrhenius rate constant.An obvious kinetic compensation effect was observed in a plot of lnA vs E for a given sample at different concentrations or for the same set of ARC data analyzed with different reaction orders n.Although the calculated lnA and E values using the dynamic differential scanning calorimetry data were usually lower than those using the adiabatic ARC data,a significant kinetic compensation effect existed between the two sets of results.This result suggested that the kineticcompensation effect existed between the activation energy and pre-exponential factor in reactions with the same or similar reaction mechanisms,regardless of the temperature control mode.

Kinetic compensation effect;Adiabatic model;Dynamic model;Activation energy; Pre-exponential factor

October 6,2015;Revised:November 2,2015;Published on Web:November 2,2015.

O643；O642

*Corresponding author.Email:clp2005@hotmail.com;Tel:+86-25-84315526-8004.

The project was supported by the National Natural Science Foundation of China(51204099)and Science and Technology Plan Projects of Jiangsu Entry-Exit Inspection and Quarantine Bureau,China(2014KJ59).

國家自然科學基金(51204099)和江蘇出入境檢驗檢疫局科技計劃(2014KJ59)資助項目

?Editorial office ofActa Physico-Chimica Sinica