醫院手術調度問題的兩階段魯棒優化方法研究

王 昱，唐加福

（1.東北大學流程工業綜合自動化國家重點實驗室，遼寧 沈陽110819；2.沈陽農業大學經濟管理學院，遼寧 沈陽110866；3.東北財經大學管理科學與工程學院，遼寧 大連116025）

醫院手術調度問題的兩階段魯棒優化方法研究

王 昱1,2，唐加福3

（1.東北大學流程工業綜合自動化國家重點實驗室，遼寧 沈陽110819；2.沈陽農業大學經濟管理學院，遼寧 沈陽110866；3.東北財經大學管理科學與工程學院，遼寧 大連116025）

手術服務時間受患者身體狀況，醫生技術水平等因素影響，具有不確定性.如何有效地調度患者手術成為醫院管理的一大挑戰.研究了醫院的手術調度問題，以院方收益最大為目標，在考慮患者最遲手術日期限制的情況下，建立了手術調度問題的確定型模型.進一步考慮手術服務時間的不確定性，將手術的服務時間表示為有界區間，考慮了管理者風險偏好對患者服務時間不確定集的影響，在確定型模型的基礎上，提出了區間型手術調度問題的兩階段魯棒優化方法.數值實驗結果表明，將魯棒優化運用于手術調度問題，能夠減小服務時間不確定性給醫院效益帶來的影響.同時，考慮最遲手術日期會降低醫院收益，最大收益差可達到10.7%.

1 引 言

近年來，我國醫改各項工作不斷推進，隨著醫療體制改革的深化，醫療服務業引發了全社會的關注.醫療機構自負盈虧，在有限的醫療服務資源和激烈的市場競爭雙重壓力下，醫院管理者越來越重視醫院效率和服務品質.手術部在醫院利潤中所占的比例最大［1,2］，且服務品質直接關系到患者的健康乃至生命，因此，手術部受到管理者和病人的高度重視.優化安排患者手術日程，提高醫院收益，減少患者調度過程中的不合理現象，創造一個良好的就診環境成為手術部管理者的目標.所謂手術調度問題，實質上是根據患者需求和醫院的手術能力，產生一段時間內，滿足一定約束條件的手術時間表的過程.廣義的手術調度除手術時間的調度外，還包括手術地點、醫護人員、手術器械等相關資源的調度.科學、合理、高效的手術安排更加人性化，使患者在較為合理的時間段進行手術，良好的控制病情的發展；同時高效的利用的手術資源，為醫院帶來了巨大的經濟效益.

醫院的手術服務時間具有較大的不確定性，手術時長受醫生技能水平、疲勞程度、患者身體狀態等多方面因素影響，難以準確給出手術服務時長的確定值.因此，在考慮手術服務時間為定長情況下的手術調度方案魯棒性較差，在醫院實際運作中往往偏差較大甚至無法實施.手術服務的內在不確定性給院方手術調度帶來了巨大的困擾，近年來，手術調度問題也吸引了學者的關注.隨機規劃和魯棒優化方法是解決不確定問題的強大工具.隨機規劃方法需要已知隨機參數的分布函數.通過對大量的歷史數據的分析，Strum等［3］發現手術服務時間可以近似用對數正態或者正態分布來描述.Lamiri等［4］假定手術需求服從正態分布，提出了手術室能力分配的隨機規劃模型，并使用蒙特卡羅近似法模擬患者的需求情景，將隨機規劃模型轉換為標準的混合整數規劃模型進行求解.Batun等［5］獲取了愛爾蘭某醫院的患者就診數據，模擬患者服務時間的分布函數，以醫院最小運作成本為目標建立了兩階段隨機規劃模型，決策患者的手術順序、時間及地點.

隨機規劃方法依賴于歷史數據和分布規律.然而，在醫院的實際調度當中，患者的就診數據往往是不充足的，難以準確描述患者服務時間的分布.因此，我們使用魯棒優化方法來求解手術調度問題.不確定優化問題的魯棒解是最壞不確定情景下使目標函數具有最優值的解，它的一個重要特點是對于任何具體的情景，魯棒解只是近似最優解，但是對于整個不確定集合是最優的［6,7］.傳統的優化方法在系統的內部參數或者外部環境變化時往往顯得無能為力，得到的優化結果與實際偏差很大.魯棒優化方法在系統的內部結構和外部環境發生變化時，仍然能夠保持系統的功能［8］.因此，魯棒優化在求解不確定優化問題時凸顯了其巨大的優勢.

在手術調度系統中，來自手術操作過程、術中突發狀況等不確定性都會直接影響到調度方案能否順利實施.在這些不確定因素的作用下，魯棒性成為能否確保醫院手術部收益和患者服務質量的重要因素.在國際上，魯棒優化在醫院管理中的應用還處于起步階段.迄今為止，使用魯棒優化方法求解手術室優化調度問題的文章只有3篇.2010年，Denton等［9］首次將魯棒優化方法應用到醫院手術室優化調度中，文章考慮了手術時長的不確定性，以最小化手術室運作成本為目標的建立了手術室分配問題的魯棒優化模型，并解析的推導出手術室最優開放數量的上下界.2012年，Mannino等［10］提出了醫院手術班次調度的新型模式，以最小化手術室的超時開放成本為目標建模，使用light robustness的方法減小手術需求波動給醫院運作成本帶來的不利影響；2013年，Holte和Mannino［11］在手術班次調度的模式下，研究了手術室資源的優化分配問題，文章考慮了各科室的患者需求的不確定性，以患者等待的隊列最短為目標，建立了問題的魯棒優化模型，并開發了行列生成算法求解此問題.

本文在Denton等［9］工作的基礎上，進一步人性化地考慮了患者的最遲手術日期限制，采用“收益管理”的思想對醫院手術室調度問題建模，并分析了管理者風險偏好系數和最遲手術日期對醫院收益和運作成本的影響.文章主要完成了以下幾個部分工作：1）在考慮患者最遲手術日期限制的情況下，建立了手術調度問題的確定型模型.2）將患者的手術服務時間表示為有界區間，利用Bertsimas［12,13］等的思想，引入管理者風險控制參數，建立了區間型手術調度問題的相對魯棒優化模型.使用對偶理論將Max-min形式的魯棒優化模型轉化為標準的混合整數規劃模型，使用優化軟件ILOG CPLEX求解.3）在實驗設計部分，使用魯棒優化和隨機規劃兩種方法求解算例，比較魯棒優化方法的求解性能.應用魯棒優化方法求解了醫院的實際案例.

2 手術調度問題

考慮醫院某科室一周（D=5天）的手術安排.科室有N個患者等待手術，主治醫生根據患者病情及入院時間給定患者的最晚手術日期Di.為確保患者在等待手術期間病情穩定且等待時間不會過長，醫院要求在最晚手術日期前一定要為患者安排手術.科室設有手術室K個，手術室日規定開放時長為T小時，開放一個手術室的固定成本為cf.若手術計劃在手術室規定開放時間內未能完成，則需要加班，單位加班費用為cv，由于醫務人員加班費用昂貴，cv＞cf/T.患者i的手術時長為ti，醫院為患者i手術可獲得收入為ci.決策患者的手術日期和地點，使醫院在一周的總收益最大.

定義決策變量如下：

xikd=1表示安排患者i在手術室k的第d天手術；否則xikd=0；

ykd=1表示手術室k在日期d開放；否則ykd=0.

okd為中間變量，表示手術室k在第d天的加班時長.

2.1 手術調度問題的確定性模型

假定患者的手術服務時間為常數，即患者的手術時長為確定已知的，手術調度模型（surgery scheduling model，SSM）如下

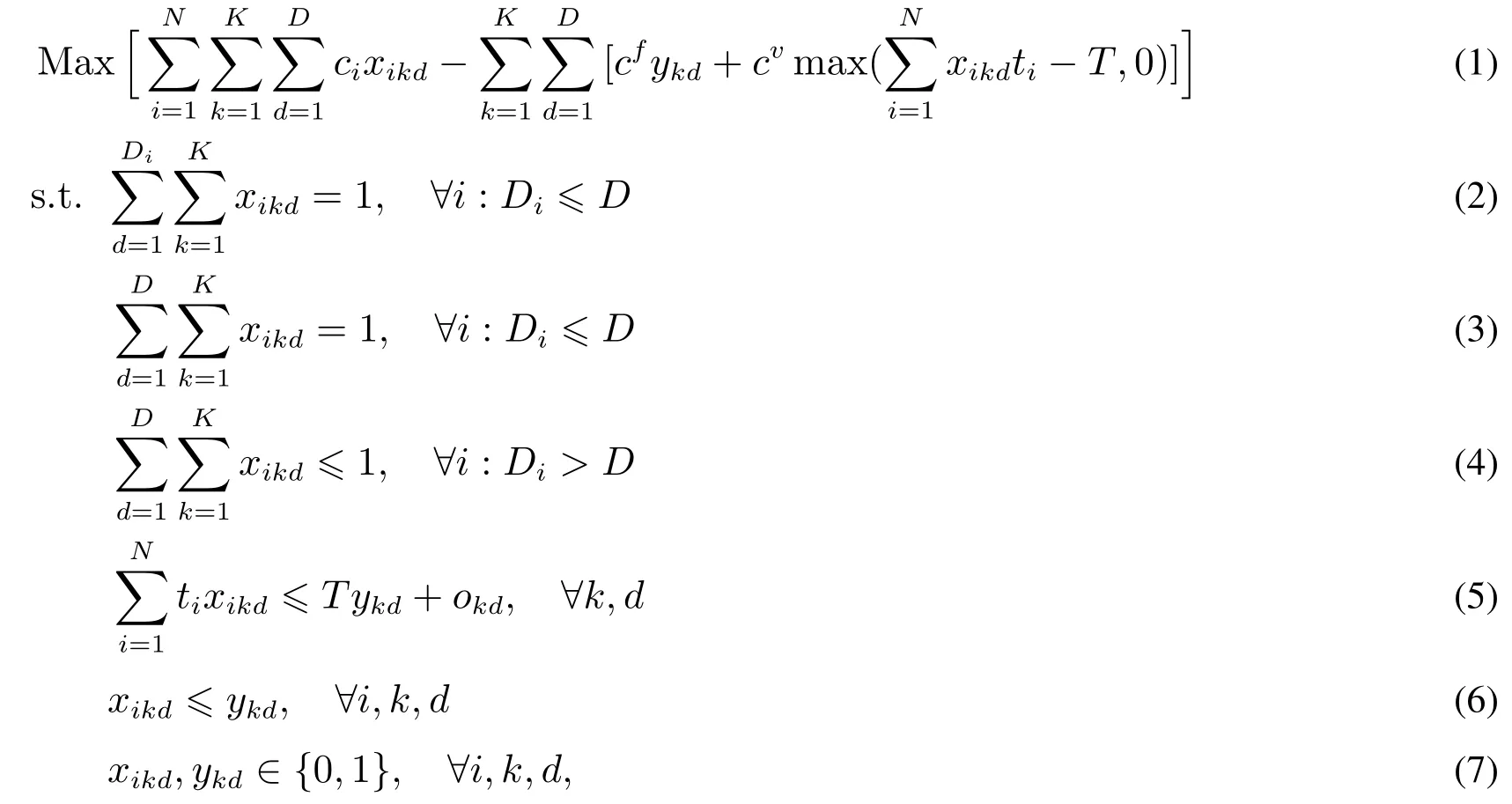
目標（1）分為兩部分，第一部分表示院方獲得的手術總收入，第二部分表示與開放手術室數量及加班時長相關的手術室運作成本，目標（1）表示最大化一個調度周期內醫院的總收益.約束（2）和（3）表示當患者的最遲手術日期在當前調度周期內時，患者在最遲手術日前一定被安排手術且只安排一次.約束（4）表示若患者的最遲手術時間晚于當前調度周期，患者至多被安排一次手術.約束（5）為手術室的日手術能力約束.約束（6）表示決策變量的關系.

圖1 患者的實際手術時長與上下界的關系Fig.1 The relationship between the actual surgery duration and its upper and lower bound

2.2 手術調度問題的兩階段魯棒模型

在SSM模型中，患者的手術時間被設置為定長.但在實際手術調度中，由于患者的手術時長ti受醫生技術水平、疲勞程度、患者身體狀況等眾多因素影響，在術前是無法準確預測的，患者的預期服務時長和實際值往往存在偏差，患者的服務時間稍有波動就可能使得原有的調度方案遠離最優，甚至不可行.因此，作者采用魯棒優化方法求解不確定服務時間下的手術調度問題.魯棒優化考慮的是最壞情況下的最好，它代表了一種保守的觀點，得到的優化方案并不一定是“最優”的.但是當不確定參數發生擾動時，得到的解仍然可行.本文假定患者的手術服務時間為連續的區間數，以最大化手術科室收益為目標，將不確定服務時間下的手術調度問題描述為一個極大化極小的優化模型，并通過對偶等理論將模型轉化為標準的混合整數線性規劃模型.

主治醫生根據診療經驗給出每位患者服務時間的上下界，則患者的服務時長可表示為連續的區間數，令δikd為患者i分配到手術室k的第d天的實際手術時長，則.定義參數? =，?表示患者的服務時長偏離下界的程度，如圖1.?=0時，所有患者的手術時間取下界（最好值）；?=1時，所有患者的手術時間取得上界ti（最差值），?的取值范圍是［0，1］.

本文使用了Bertsimas和Sim［12,13］的思想來控制魯棒模型的保守程度.對于周期D內所有調度的患者引入約束

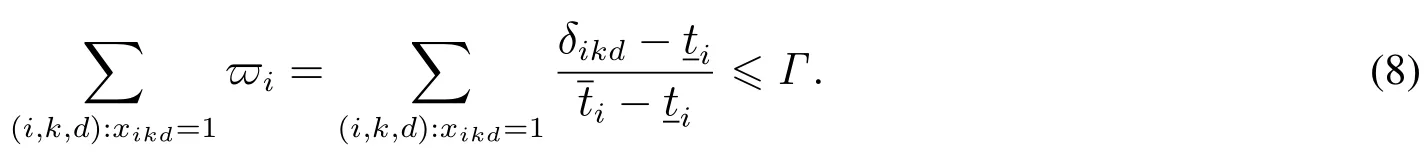
式（8）表示最多有Γ個患者的手術時間同時達到最差值（上界）.參數Γ的取值大小由管理者事先給定，反映了醫院管理者的風險偏好程度，0≤Γ≤N.Γ=0時，此問題為確定型問題，表示所有患者的手術時間均為下界（最好情況）；Γ=N時，表示所有患者的手術時間均為上界（最差情況）.根據決策者的風險偏好程度，調整Γ的取值.若決策者較為保守，則設定Γ取值較大；反之取值較小.

由此，患者手術時長的不確定集表示為

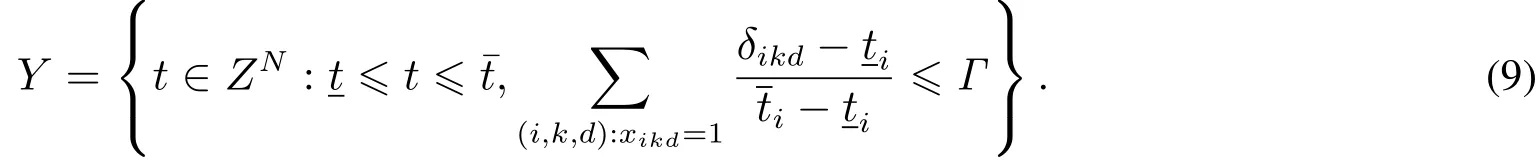
重新建立魯棒優化模型（robust surgery scheduling model，RSSM）：魯棒優化是求得一個這樣的解，使得最壞情況下的目標函數最優，最大化最壞情況下的醫院手術部的利潤，即

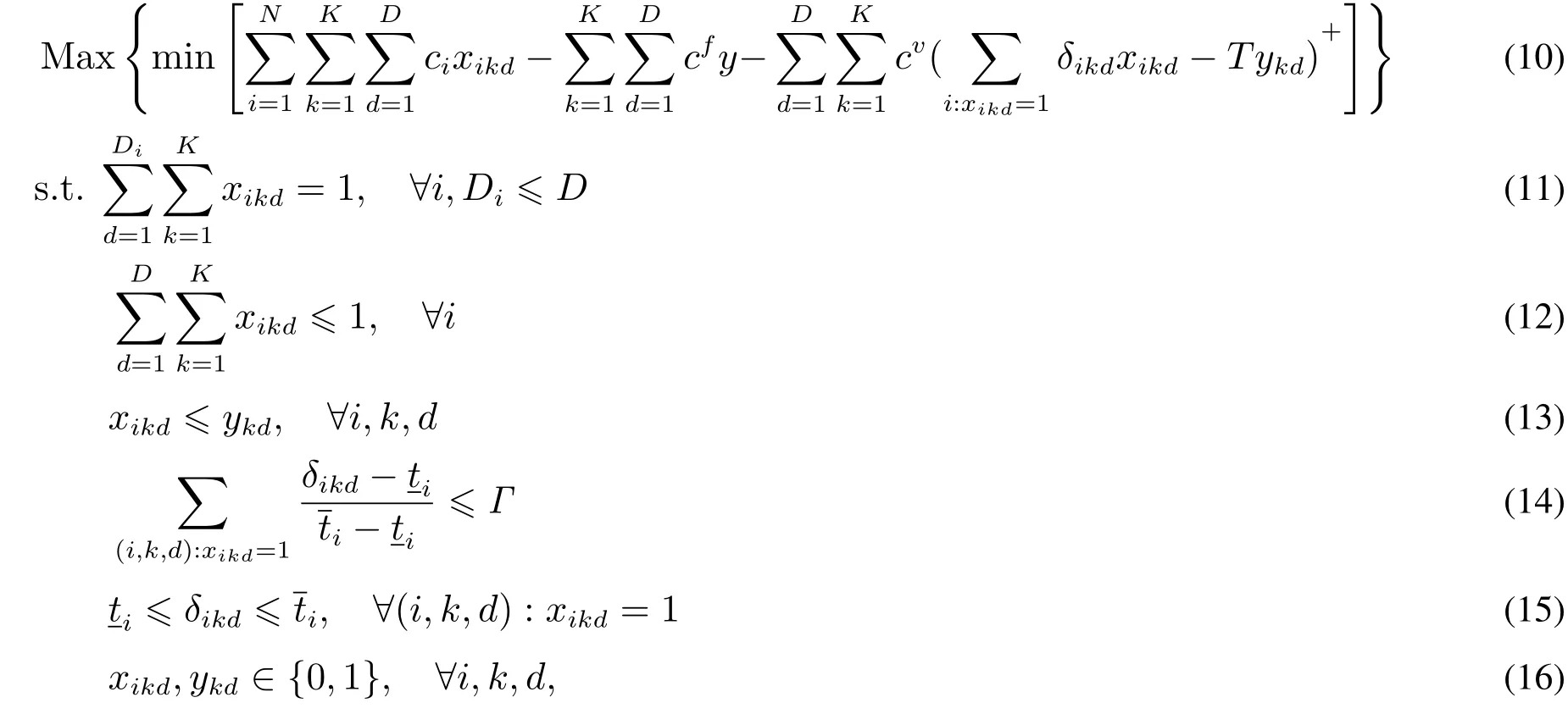
約束（14），（15）組成了手術服務時間的不確定集合.目標（10）表示在不確定集合取得最差情景下，醫院的收益最大.在模型RSSM中，發現只有目標函數（10），約束（14）和（15）受手術服務時長不確定性的影響，因此，RSSM模型可以表示為兩階段魯棒優化模型，第一階段的決策變量為xikd，ykd，第二階段的決策變量為δ.

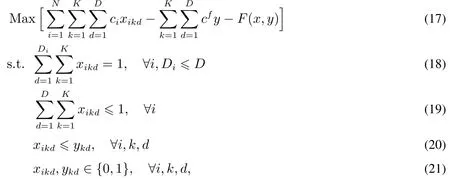
其中F（x,y）是與手術室超時開放時長相關的費用，即

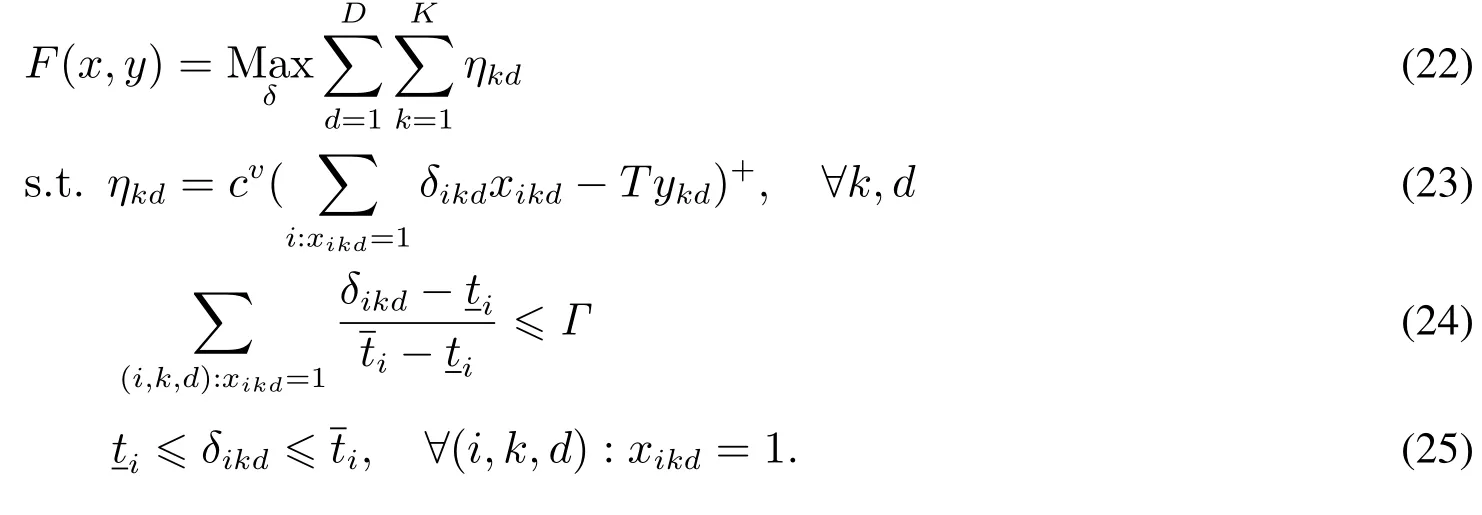
2.2.1模型轉化

為了使得F（x,y）可以代入原模型中直接求解，需要引入對偶理論對模型F（x,y）進行變換，首先使用Denton等［9］方法化簡F（x,y）的表達式.引入決策變量zkd，zkd=1表示有手術室k在第d天有超時開放現象發生，否則zkd=0.重新建模F（x,y），即

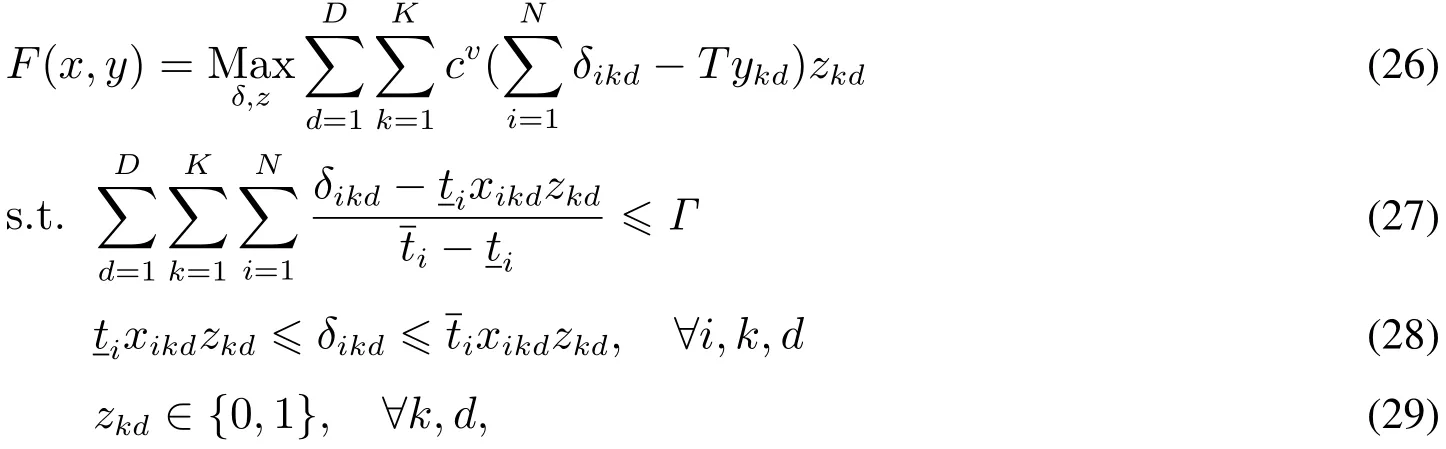
由約束（28）可知，zkd=0，則δikd=0.因此，目標函數可以化簡為

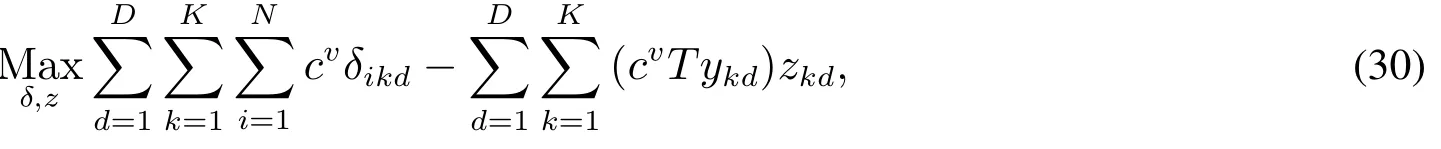
F（x,y）由非線性化簡為線性規劃問題，即

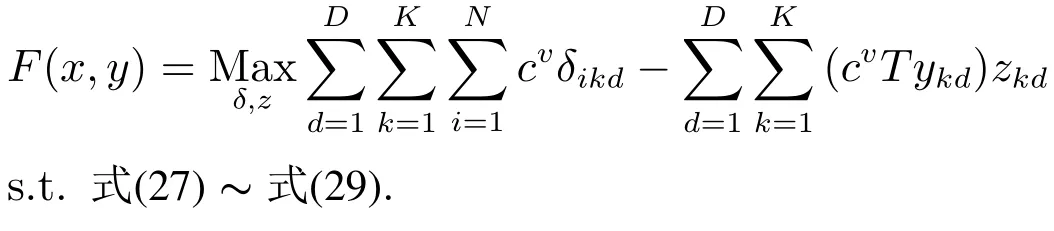
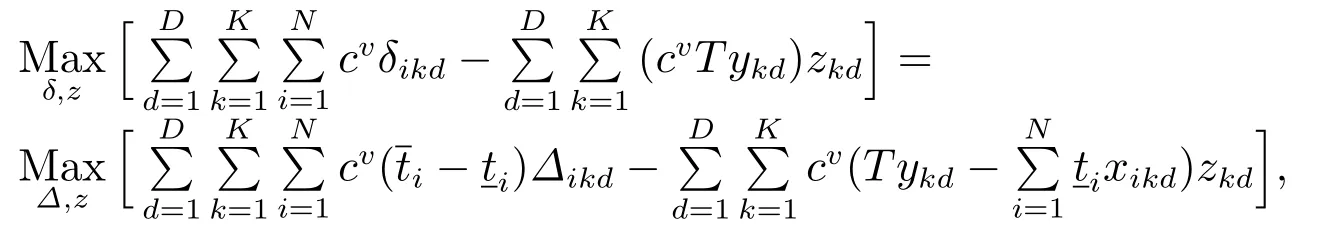
模型F（x,y）可以重新表達為

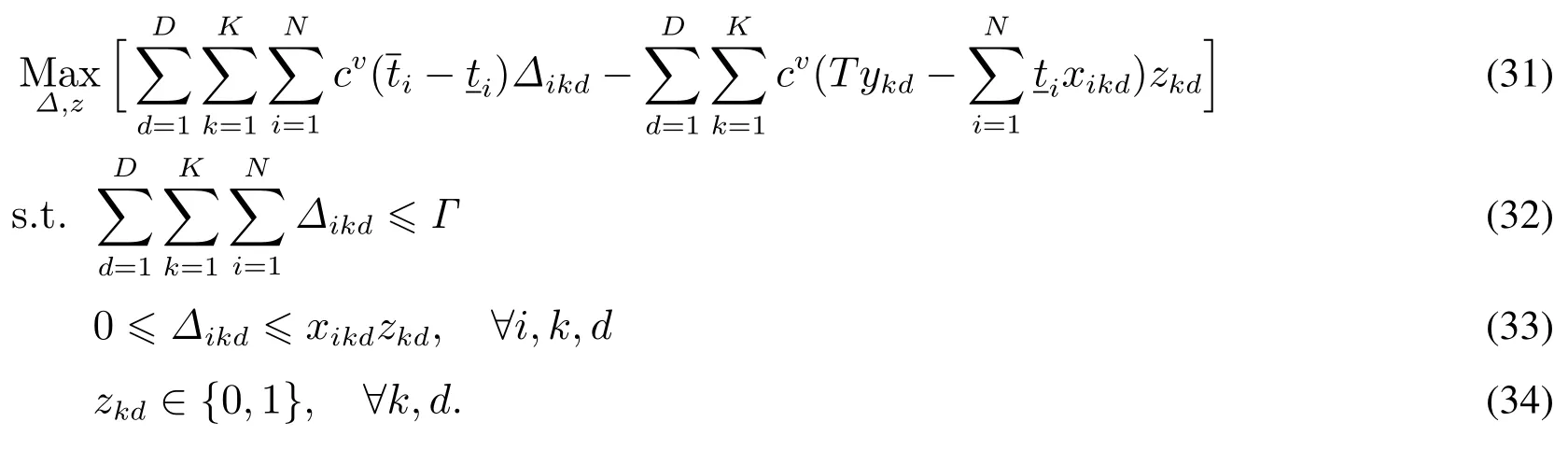
上述模型為線性規劃模型，由于線性規劃問題的基可行解對應于可行域的頂點.若可行域有界，線性規劃問題的目標函數一定可以在其可行域頂點上達到最優，因此，由命題1可知，F（x,y）的線性松弛的解等價于原問題的解，即

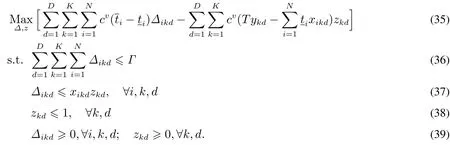
由于上述線性規劃問題式（35）～式（39）是可行且有界的，通過強對偶定理可知，原最大化問題可以等價轉化為最小化問題.定義?,ikd（i∈1,2,...,N；k=1,2,...,K；d=1,2,...,D）,?kd（k=1,2,...,K；d=1,2,...,D）為約束式（36），式（37），式（38）的對偶變量.則式（35）～式（39）的對偶線性規劃問題為

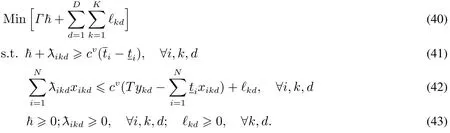
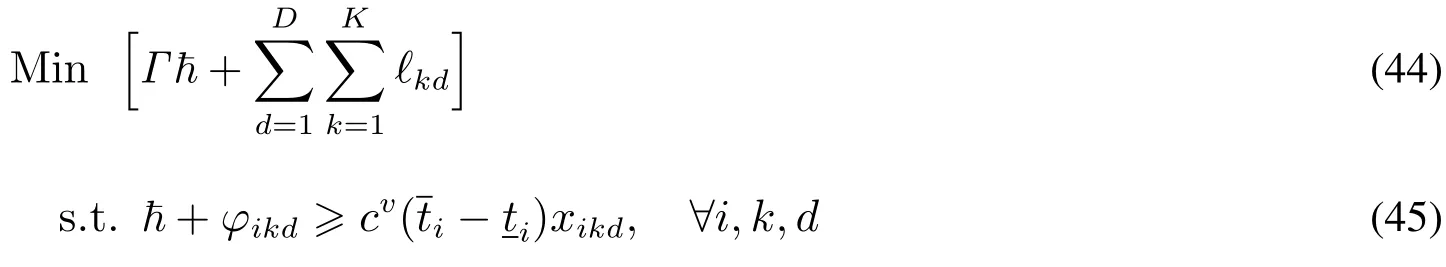
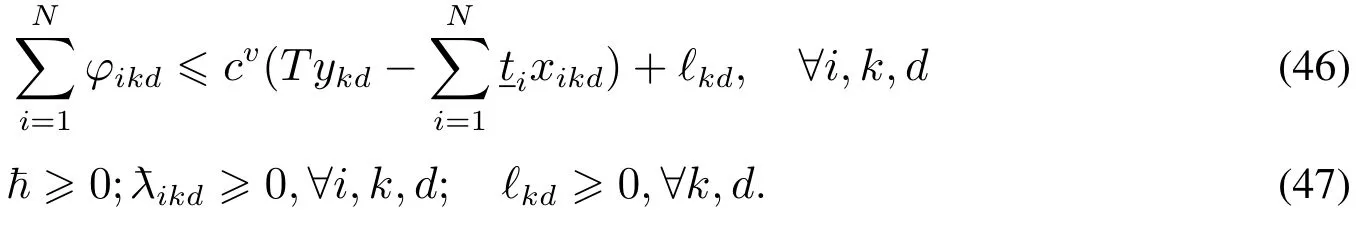
將式（44）～式（47）代入到初始模型RSSM中，得到RSSM的魯棒對等模型RSSM1

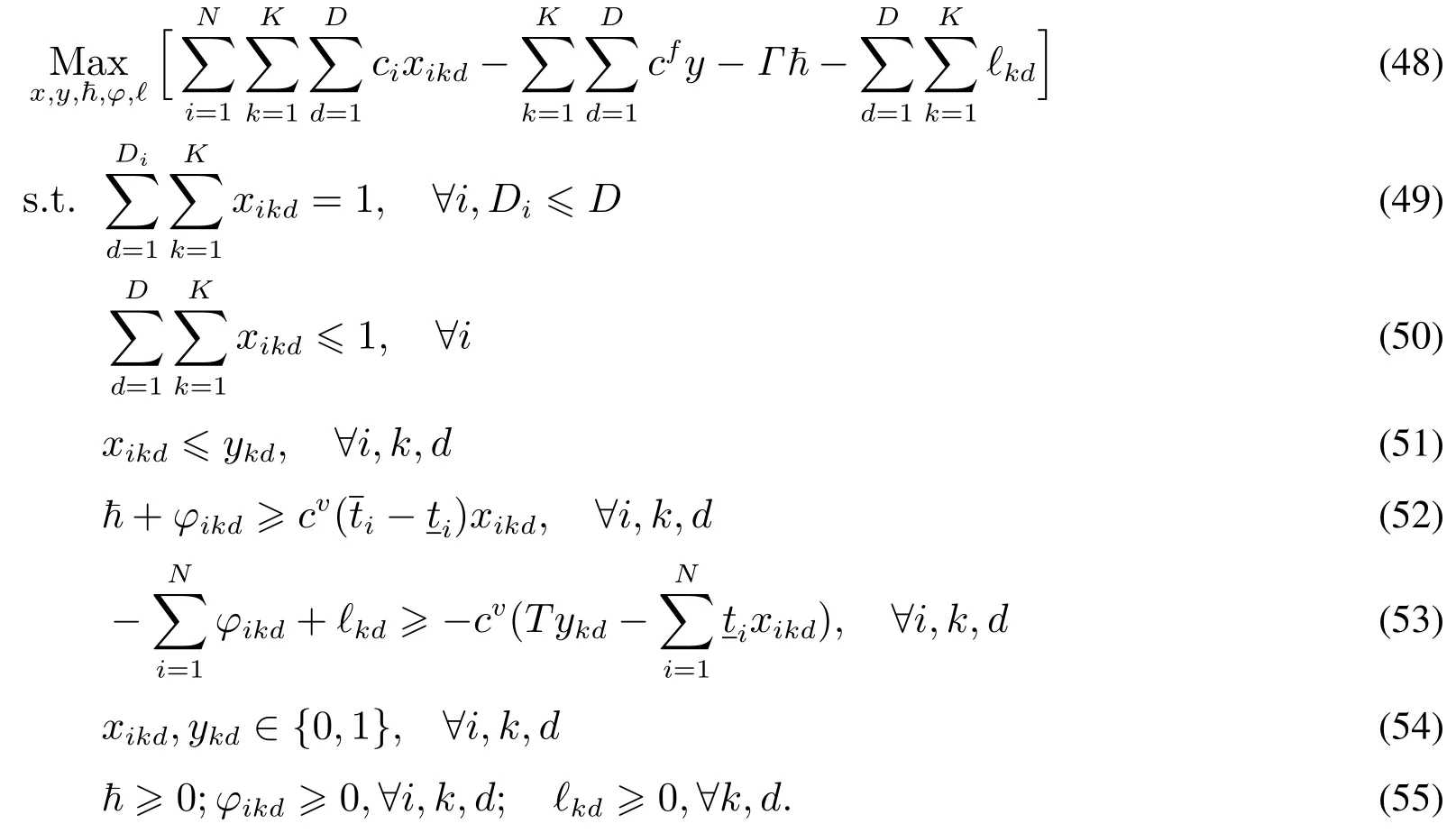
3 數值仿真

數值實驗在運行環境Dell Optiplex GX620，Intel（R）Pentium（R）D CPU 2.80GHz 2.00Gb下進行.由于模型RSSM1為標準的混合整數線性規劃模型，可以使用優化軟件ILOG CPLEX求解.在Visual studio2008平臺下使用計算機語言C#調用CPLEX12.2進行數據測試.

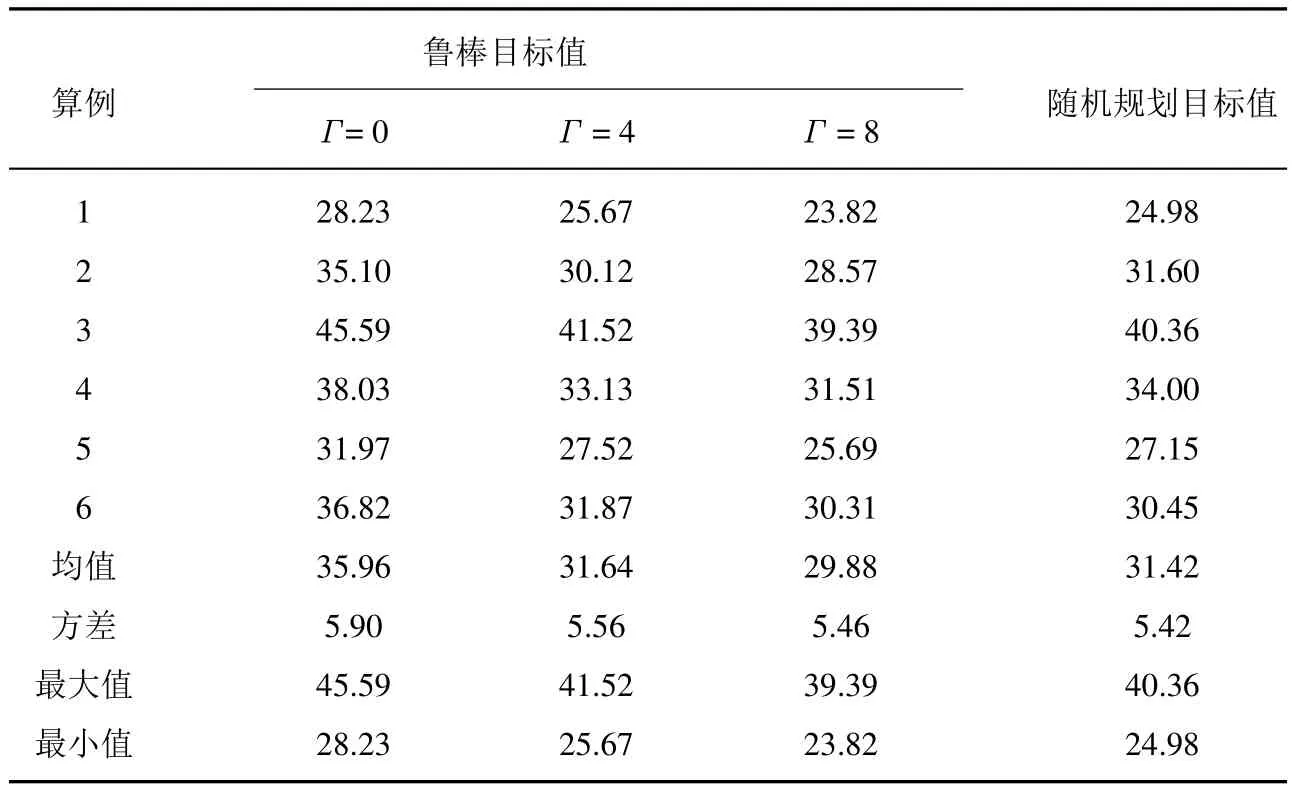
表1 魯棒優化與隨機規劃方法求解性能的比較Table 1 Comparison between the robust method and stochastic programming

為了測試魯棒優化方法的求解性能，首先將魯棒優化方法與隨機規劃方法進行比較.取指數分布函數的40%和60%為患者手術時間的上下界，患者的手術時長為有界區間，上下界取值在區間［20，200］隨機產生.假定患者的手術服務時間服從正態分布，取上下界的均值為正態分布的均值，在給定分布下采樣模擬患者手術時長的可能情景，樣本數量取值為50，使用隨機規劃和魯棒優化兩種方法求解手術調度問題.問題的其他參數設定如下：N=15,T=8,cv=1,cf=4,K=2,Dcycle=5，患者的最遲手術日期在［1，10］之間取值.隨機產生6組實例進行測試，由表1可見，當Γ=4，隨機規劃與魯棒優化的求解結果近似相同；然而，兩種方法的求解效率相差很大.魯棒優化方法的平均求解時間為41 s，隨機規劃的平均求解時間為370 s.因此，魯棒優化方法在問題的求解效率上凸顯了優勢.

為了說明Γ取值對魯棒優化方法的影響，使用大連大學附屬新華醫院肛腸科1獲得的6組實例，在兩種參數設定cf/T＜cv＜ci/，cf/T＜ci/i＜cv情況下進行實驗.當cf/T＜cv＜ci/i，ci/i∈（1，2），患者數為45時，求解結果如表2、圖2所示.根據決策者的風險偏好程度改變參數Γ的取值，Γ取值越大，表示決策者越保守，Γ取值越小，表示決策者越偏好風險.由表2、圖2可以得到如下結論：

表2 cf/T＜cv＜ci/i時，參數Γ對醫院收益的影響Table 2 The influence of the parameter Γ on hospital's revenue with cf/T＜cv＜ci/i

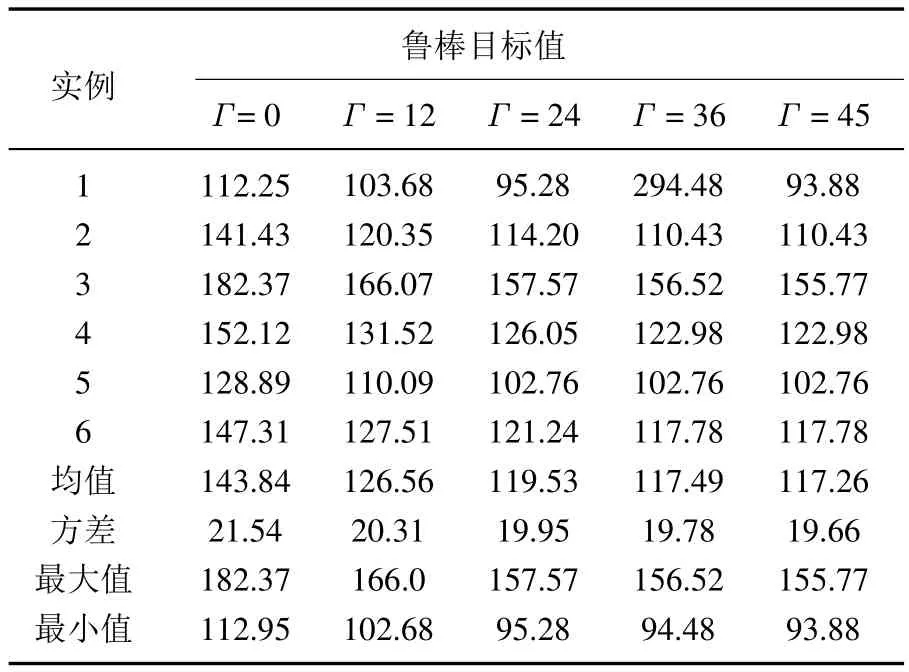
表2 cf/T＜cv＜ci/i時，參數Γ對醫院收益的影響Table 2 The influence of the parameter Γ on hospital's revenue with cf/T＜cv＜ci/i

魯棒目標值實例 Γ=0 Γ=12 Γ=24 Γ=36 Γ=45 1 112.25 103.68 95.28 294.48 93.88 2 141.43 120.35 114.20 110.43 110.43 3 182.37 166.07 157.57 156.52 155.77 4 152.12 131.52 126.05 122.98 122.98 5 128.89 110.09 102.76 102.76 102.76 6 147.31 127.51 121.24 117.78 117.78均值 143.84 126.56 119.53 117.49 117.26方差 21.54 20.31 19.95 19.78 19.66最大值 182.37 166.0 157.57 156.52 155.77最小值 112.95 102.68 95.28 94.48 93.88

表3 cf/T＜ci/i＜cv時，參數Γ對醫院收益的影響Table 3 The influence of the parameter Γ on hospital's revenue with cf/T＜ci/i＜cv

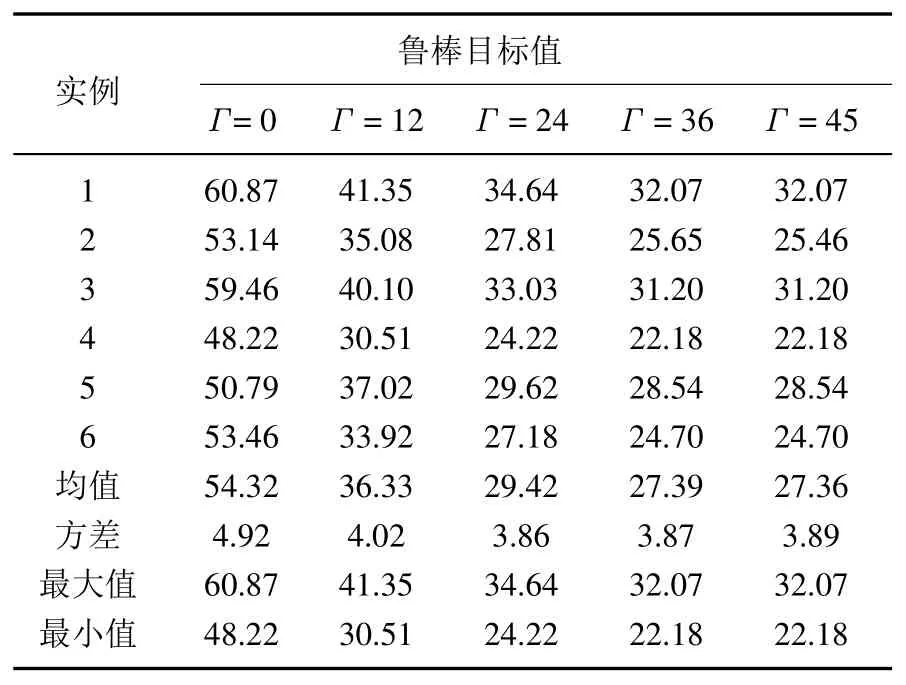
表3 cf/T＜ci/i＜cv時，參數Γ對醫院收益的影響Table 3 The influence of the parameter Γ on hospital's revenue with cf/T＜ci/i＜cv

Γ=36 Γ=45 32.07 32.07 25.65 25.46 31.20 31.20 22.18 22.18 28.54 28.54 24.70 24.70 27.39 27.36 3.87 3.89 32.07 32.07最小值 48.22 30.51 24.22 22.18 22.18

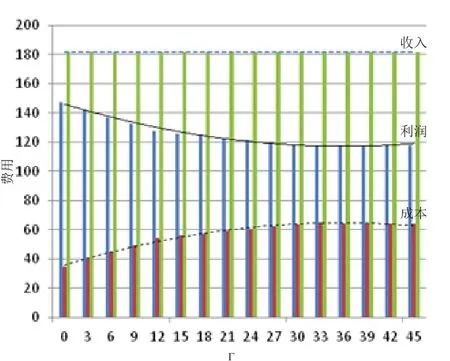
圖2 cf/T＜cv＜ci/i時，參數Γ對利潤、收入和成本的影響Fig.2 The influence of the parameter Γ on revenue，income and cost with cf/T＜cv＜ci/i

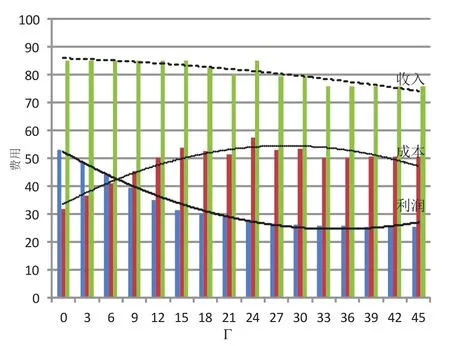
圖3 cf/T＜ci/i＜cv時，參數Γ對利潤、收入和成本的影響Fig.3 The influence of the parameter Γ on revenue，income and cost with cf/T＜ci/＜cv

解的保守性隨著Γ的增加而增強.隨著Γ的增加，醫院的利潤呈現單調非增的趨勢，即管理者規避風險降低了醫院的收益.醫院的管理者可以根據不同的風險偏好程度選擇Γ的取值，進而獲得醫院的患者手術調度方案.

當醫院的手術能力充足，且cf/T＜cv＜ci/i時，對于所有的風險偏好系數Γ取值，醫院的總收入相同（見圖2），這是由于所有患者都被安排手術時醫院的總收益值達到最大.隨著Γ的增加，醫院的手術成本以及開放手術室的數量呈現單調非減的趨勢.

當cf/T＜ci/i＜cv，ci/i∈（0.5,1），患者數為45時，求解結果如表3、圖3所示.根據表3和圖3的實驗結果，可以得到如下結論：

解的保守型隨著Γ的增加而增強.隨著Γ的增加，醫院的利潤呈現單調非增的趨勢，即管理者規避風險降低了醫院的收益.

隨著Γ的變化，醫院的手術收入呈現不規則變化（如圖3），這說明即使醫院的手術能力充足，在cf/T＜ci/i＜cv范圍內，并非所有的患者都被安排手術，而且存在著患者選擇.隨著Γ的增加，醫院的手術成本呈現不規則變化，有增加的趨勢.

為了避免患者入院后遲遲安排不上手術，或者患者入院后因未及時治療導致的病情惡化，本文的模型中，更加人性化的引入了患者最遲手術日期.患者入院檢查后，由其主治醫生根據患者入院時間和病情規定最遲手術時間，確保患者在最遲手術日期前接受治療.為了進一步說明考慮最遲手術時間對醫院收益、運作成本等因素的影響，將引入最遲手術日期的模型與不考慮此因素的方法進行比較，獨立重復進行十組實驗.圖4為不同Γ下，十組實驗中手術科室的平均收入、成本和利潤.根據表4和圖4的實驗結果可以發現，考慮最遲手術時間會降低醫院的收益，最大收益差為10.7%.考慮最遲手術時間時，手術室的平均運作成本更高.

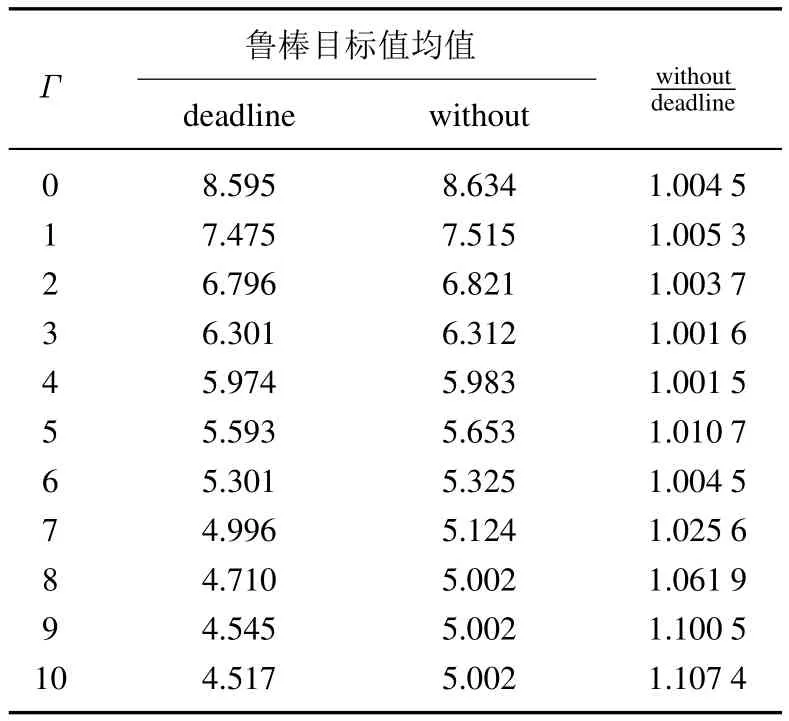
表4 最晚手術日期對醫院利潤的影響Table 4 The influence of surgery deadline on hospital's revenue

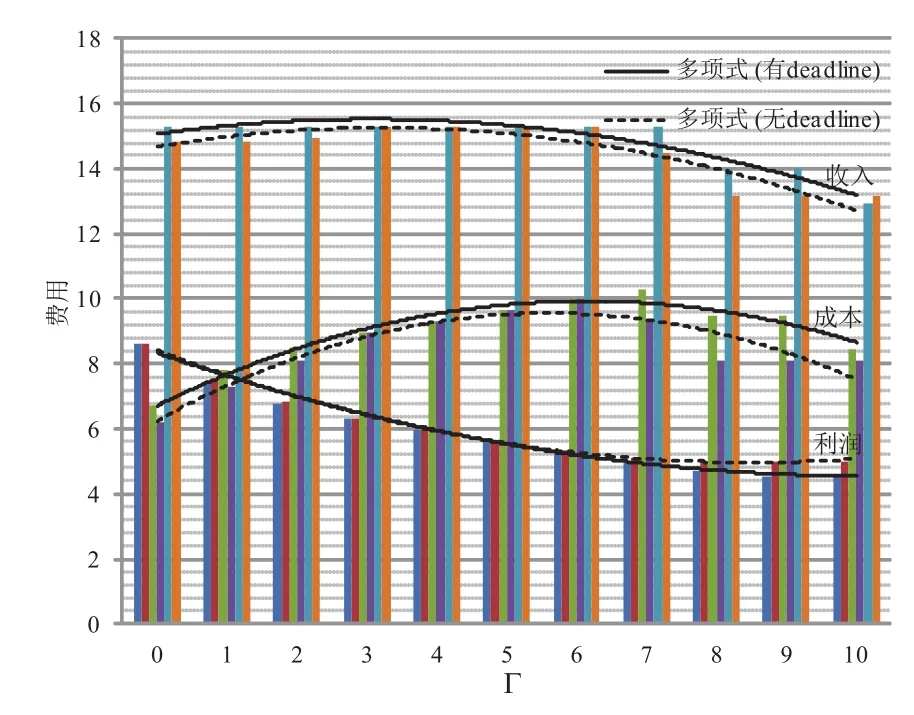
圖4 最晚手術日期對手術部的利潤、收入和成本的影響Fig.4 The influence of surgery deadline on revenue，income and cost

4 結束語

本文在考慮患者最遲手術日期情況下，對區間型患者服務時長的手術調度問題進行研究.在引入管理者風險控制參數的情況下，以最大化醫院收益為目標，建立了手術調度問題的魯棒優化模型.該方法在應對患者服務時間波動時，具有良好的魯棒性.將提出的魯棒優化方法與隨機規劃方法進行比較，驗證了方法在求解效率上的優勢.實驗結果表明，將魯棒優化運用于手術調度問題，能夠減小服務時間不確定性給醫院效益帶來的影響.同時，考慮最遲手術日期會降低醫院收益，最大收益差可達到10.7%.

［1］Bowers J，Mould G.Ambulatory care and orthopaedic capacity planning.Health Care Management，2005，8（1）：41—47.

［3］Strum D P，Jerrold M D，May H，et al.Modeling the uncertainty of surgical procedure times comparison of log-normal and normal models.Anesthesiology，2000，92（4）：1160—1167.

［4］Lamiri M，Grimaud F，Xie X L.Optimization methods for a stochastic surgery planning problem.International Journal of Production Economics，2009，120（2）：400—410.

［5］Batun S.Operating room pooling and parallel surgery processing under uncertainty.INFORMS Journal on Computing，2011，23（2）：220—237.

［6］吳小歡，朱金福，吳薇薇.航線網絡區間型相對魯棒優化設計.系統工程學報，2012，27（1）：69—78. Wu X H，Zhu J F，Wu W W.Relative interval robust optimization of airline network designing.Journal of Systems Engineering，2012，27（1）：69—78.（in Chinese）

［7］許曉晴，崔文田，林 軍，等.基于最小最大遺憾的同型并行機魯棒調度模型.系統工程學報，2013，28（6）：729—737. Xu X Q，Cui W T，Lin J，et al.Robust identical parallel machines scheduling model based on min-max regret criterion.Journal of Systems Engineering，2013，28（6）：729—737.（in Chinese）

［8］田文迪，胡慕海，崔南方.不確定性環境下魯棒性項目調度研究綜述.系統工程學報，2014，29（1）：135—144. Tian W D，Hu M H，Cui N F.Review of studies on robust project scheduling under uncertainty.Journal of Systems Engineering，2014，29（1）：135—144.（in Chinese）

［9］Denton B T，Miller A J，Balasubramanian H J.Optimal allocation of surgery blocks to operating rooms under uncertainty.Operations Research，2010，58（4）：802—816.

［10］Mannino C，Nilssen E J，Nordlander T E.Apattern based，robust approach to cyclic master surgery scheduling.Journal of Scheduling，2012，15（5）：553—563.

［11］Holte M，Mannino C.The implementor/adversary algorithm for the cyclic and robust scheduling problem in health-care.European Journal of Operational Research，2013，226（3）：551—559.

［12］Bertsimas D，Sim M.The price of robustness.Operations Research，2004，52（1）：35—53.

［13］Bertsimas D，Sim M.Robust discrete optimization and network flows.Mathematical Programming，2003，98（1/3）：49—71.

A two-stage robust optimization method for solving surgery scheduling problem

Wang Yu1,2，Tang Jiafu3
（1.State Key Lab of Synthetic Automation of Process Industry，Northeastern University，Shenyang 110819，China；2.The College of Economics and Management，Shenyang Agricultural University，Shenyang 110866，China；3.College of Management Science and Engineering，Dongbei University of Finance and Economics，Dalian 116025，China）

The surgery service duration，which is influenced by individuals' physical conditions，the surgeon's skills，and so on，is uncertain in advance.How to effectively schedule surgeries is a challenge for managers in hospitals.This paper studies a surgery scheduling problem with regard to surgery deadline.Firstly，a deterministic surgery scheduling model is built with the objective of maximizing the revenue of surgery department.Then，the uncertain surgery service durations are represented as bounded intervals，and a two-stage robust optimization approach for solving surgery scheduling is described with a risk-preference parameter.The computational experiments prove that the proposed robust optimization method helps to reduce the influence of uncertainty on the hospital's revenue.In view of surgery deadline，the hospital's revenue reduces with a maximum level of 10.7%.

robust optimization；uncertain surgery duration；operating room scheduling；hospital management

10.13383/j.cnki.jse.2016.04.001

王 昱（1987—-），女，遼寧鐵嶺人，博士生，研究方向：優化與調度，魯棒優化，醫療服務業運作管理，Email：wangyuguomei@ 163.com.

2014-01-17；

2014-09-04.

國家自然科學基金資助項目（71021061）；教育部博士點專項基金資助項目（20120042110023）；

唐加福（1965—-），男，湖南東安人，博士，教授，博士生導師，研究方向：制造系統生產與物流運作管理，服務系統運作優化等，Email：jftang@mail.neu.edu.cn.