基于GPU的并行條件模擬算法及其在儲量估算中的應用

王冰怡， 鄧維科， 余先川

(北京師范大學信息科學與技術學院，北京100875)

?

基于GPU的并行條件模擬算法及其在儲量估算中的應用

王冰怡， 鄧維科， 余先川

(北京師范大學信息科學與技術學院，北京100875)

條件模擬是一種計算非常耗時的高精度三維插值算法。針對串行條件模擬算法計算時間過長的問題，提出基于GPU的并行條件模擬算法，并進行儲量估算。對條件模擬算法進行并行分析，利用GPU的高度并行性，構建CUDA通用計算開發環境，實現串行條件模擬算法到并行條件模擬算法的轉換，使條件模擬算法的時間復雜度從O(n)降至O(logn)。并對西藏甲瑪銅礦進行了儲量估算。實驗結果表明，在安裝普通NVIDIA顯卡的計算機以及估算精度不下降的情況下，GPU并行條件模擬的計算效率比CPU串行條件模擬的計算效率提高了60倍以上。

條件模擬；GPU；并行計算；儲量估算；甲瑪銅礦；西藏

0　引　言

地質統計學是數學地質領域一門發展迅速的新興邊緣學科(王仁鐸等，1988)，在優化采樣方案、處理不規則采樣及最優化插值計算等方面具有明顯的優點。條件模擬是地質統計學中迅速發展的一門新技術，是一種新的蒙特卡羅(Monte Carlo)方法。采用條件模擬方法得出的模擬值，不僅能與已知數據Z(x)保持一致的數學期望、方差和分布函數，而且還能保持一致的協方差函數C(h)或變差函數γ(h)，同時還滿足在各已知點處的模擬值等于該點實測值的條件。條件模擬充分考慮了原始量的空間結構性、隨機性和局部變異性，較好地解決了克立格法中難以克服的平滑效應等問題(李星等，2003)。目前，條件模擬基本方法主要有轉向帶法(Brooker，1985；Dean，1995)、誤差模擬方法(Boudreault et al., 2016；Liang et al., 2016)、傅立葉變換法(Pinheiro et al., 2016)和序貫條件模擬方法(Juang et al., 2004；Sojdehee et al., 2015；Yamamoto et al., 2015；Ribeiro et al., 2016)等。其中，誤差模擬方法作為基礎方法運用最為廣泛，其主要思路為：在克立格估值的基礎上，人為增加一個被克立格法的平滑效應濾掉的隨機誤差部分。

1　串行條件模擬算法及其應用缺陷

設Z(x)是滿足二階平穩假設的局域化變量，E[Z(x)]=m并存在協方差函數C(h)或變差函數γ(h)。要求Z(x)的條件模擬為ZCS(x)，即要求獲得與Z(x)同構的區域化變量ZCS(x)的一個現實，且在已知點xa上滿足模擬值等于實測值。即：

ZCS(xa)=Z(xa),?xaa=1,2,…,n

(1)

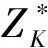
(2)

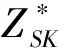
(3)

(4)

式(4)為計算誤差條件模擬的實用型公式。根據公式(4)可知，首先求出非條件模擬值ZS(x)，再對實測點xa上的誤差值[Z(xa)-ZS(xa)],a=1,2,…,n進行克立格估算，最后將二者相加得到ZCS(x)，此方法可以減少1次克立格方程組計算。

隨著已知信息的增加，估算層數眾多、網格劃分細的大型區域儲量時，串行條件模擬算法計算時間過長，無法滿足實時分析的要求(白樹仁等，2011)，并行算法是解決這一問題的一種有效方法(Pesquer et al., 2011；Hu et al., 2015；Liu et al., 2016)。利用GPU在處理通用計算時的高度并行性、優秀的浮點運算能力，構建CUDA通用計算開發環境，提出了基于GPU的并行條件模擬算法，在不失真的情況下降低了運算時間，提高了估算精確度。

2　基于GPU的并行條件模擬算法

2.1GPU與CUDA開發環境

GPU專注于解決數據并行計算的問題，具有極高的計算密度。GPU 并不要求對精密流的控制，可通過高速運算來隱藏存儲器的訪問延遲，而不必使用較大的數據緩存。

統一計算設備架構(Compute Unified Device Architecture，CUDA)是一個軟硬件協同的完整的解決方案。這種架構可以使用GPU處理復雜的科學計算問題，特別是極大數據量的并行計算問題。CUDA 在GPU 架構上將晶體管更多地投入到數據處理，減少數據緩存和流量控制對晶體管資源的消耗。

2.2并行條件模擬算法

并行條件模擬算法首先需要將地質實體網格化，將其劃分為若干規則的網格塊段。條件模擬法依據空間已知點，對待模擬網格進行條件模擬，并將所有待模擬網格相加得到礦體總儲量，其串行過程包括以下步驟。

(1) 輸入：空間已知點集合A，集合A元素為Pi(x,y,z,Z(x,y,z)),i=1,2,…,N；各向異性軸信息；輸出：條件模擬結果，即若干網格。

(2) 根據各向異性軸，對礦體實體進行網格化，將地質實體劃分為S個待模擬網格。

(3) fori= 1 toS

① 根據3個各向異性軸信息，形成1個橢球形的搜索區域；

② 以網格Gridi為橢球中心，搜索落在此橢球搜索區域內、距離該中心最近的若干空間已知點，將其保存為集合B；

③ 根據B中保存的已知點，計算待模擬網格Gridi的條件模擬結果ZSi(x,y,z)；

④ 若條件模擬為序貫方法(序貫高斯條件模擬與序貫指示條件模擬)，則需要將條件模擬結果放入已知點集合中；

end for。

(4) 根據每個網格儲量估算公式計算儲量結果Wi：

Wi=ZSi(x,y,z)·p·Vi(x,y,z)/100

(5)

式(5)中，Wi為儲量估算結果，x,y,z為網格塊段位置，ZSi(x,y,z)為該網格處的條件模擬值，Vi(x,y,z)為網格塊段體積，p為礦石體重(即密度)。

(5) 將所有待模擬網格計算后的儲量，相加得到礦體總條件模擬量W：

(6)

對于上述步驟(3)，每個待模擬的網格都是一個獨立的計算，因此可以通過并行計算的思想來開發。步驟(5)為加法運算，可用CUDA的規約方式實現并行優化。分析得到并行條件模擬插值算法步驟如下。

(1) CPU主線程：同串行條件模擬算法中的步驟(1)。

(2) CPU主線程：執行串行條件模擬算法中的步驟(2)，并將網格信息作為參數輸入CUDA的kernel核函數。

(3) CPU主線程：設置線程屬性，包括CUDA計算環境的Grid、Block中線程數。

(4) GPU各線程：對于線程i，計算網格xi對應的插值結果Zi(x,y,z)。

① 利用變異性分析結果，獲取3個各向異性軸信息，形成一個橢球形的搜索區域。

② 以網格i為橢球中心，搜索落在此橢球搜索區域內的空間已知點，將其保存。

③ 根據步驟②中保存的已知點，利用條件模擬法進行計算得到待模擬網格i的條件模擬值ZSi(x,y,z)。

④ 根據每個網格條件模擬后的結果，計算儲量，見公式(5)。

(5) GPU各線程：

① _syncthreads()； //CUDA同步函數

② i= blockDim.x/ 2；j = 1；

③ while (i != 1)

if (j < i)

then W[i] = W[i] + W[j + i]；

end if；

_syncthreads()；//CUDA同步函數

i = i/ 2；

end while；

④ return W[1]；

其中，W[1]為相加后的礦體條件模擬結果W。過程(5)將計算累積結果的算法時間復雜度從O(n)降至O(logn)，并且通過GPU并行化計算，提高了運算效率。

(6) CPU主線程：保存條件模擬結果W。

3　實驗設置與結果分析

3.1實驗設置

為了驗證基于GPU的并行條件模擬算法的效率，在Windows操作系統下，使用GPU方法與傳統CPU方法分別進行條件模擬實驗，其計算環境如下。

GPU運算平臺為NVIDIA GeForce GT445M顯卡(144 CUDA核)；GPU最低主頻1.18 GHz，動態調頻；顯存3 072 M(DDR3 800 MHz)，位寬192 bit；CUDA驅動版本4.10/4.0；CUDA運算版本2.1。操作系統Windows 7(64 bit)。

CPU運算平臺為Intel i7 Q740(4核8線程)；CPU最低主頻1.73 GHz，動態調頻；內存8 G(DDR3 1 333 MHz)。操作系統Windows 7(64 bit)。

采用西藏甲瑪銅礦實驗數據，鉆孔采樣點統計信息如表1所示。

注：數據來源于中國地質科學院礦產資源研究所

3.2實驗結果分析

條件模擬算法在CPU平臺和GPU平臺上的計算時間增長曲線如圖1所示。從圖中看出，隨著條件模擬網格數的增加，條件模擬的CPU計算時間越來越長，GPU的效率依然很高，優越性越明顯。

圖1　 CPU 與GPU 條件模擬耗時增長曲線比較Fig.1　Comparison of time-consuming growth curves of CPU and GPU conditional simulation

條件模擬在CPU 平臺與GPU 平臺的運算時間比較如表2所示。隨著網格精細程度的增加，基于CPU的條件模擬過程耗時越長，GPU的加速效果越明顯，并在達到峰值后保持平穩。

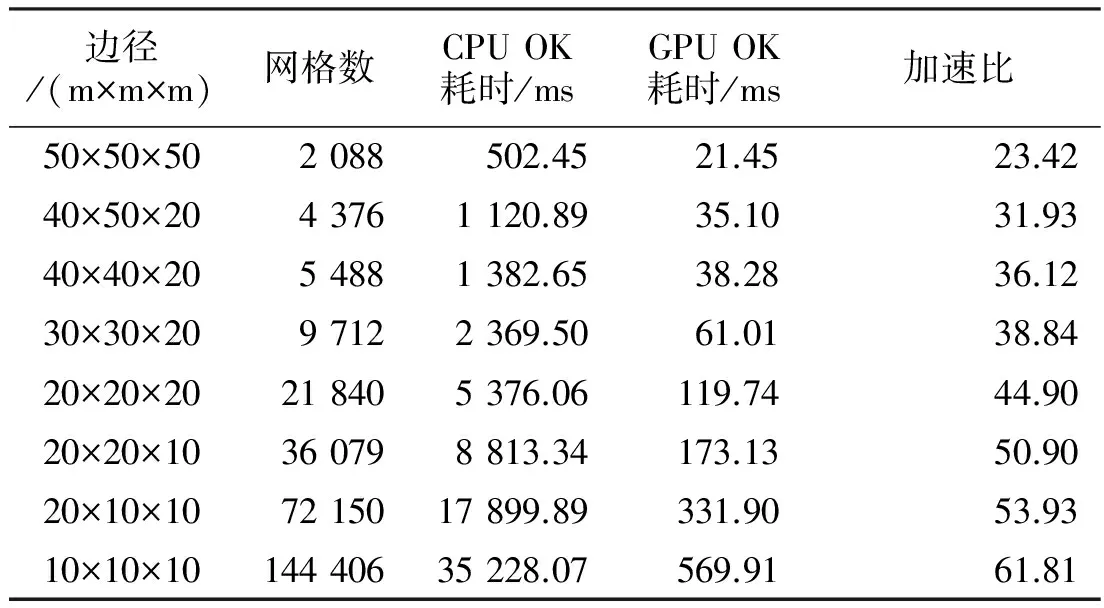
表2　CPU與GPU 的條件模擬運算時間比較

分別利用基于CPU的條件模擬和基于GPU的條件模擬，對西藏甲瑪銅礦進行儲量估算(表3)。理論上，由于條件模擬具有隨機性，GPU平臺的條件模擬結果與CPU平臺的條件模擬結果會有所差別，但均在克立格方差的可控范圍內，因此通過表3的對比分析，也同樣驗證了基于GPU將條件模擬并行化的準確性與穩定性。

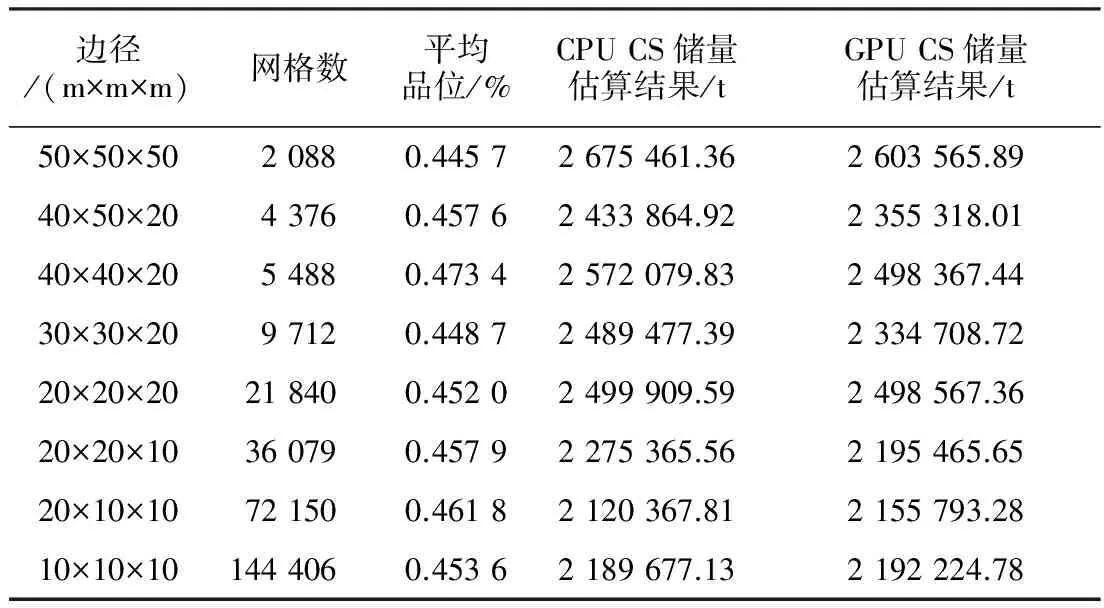
表3　CPU與GPU條件模擬的儲量估算結果比較

分析圖2的GPU加速比，可以看出：當數據數量較少時，GPU的加速效果不明顯；隨著待模擬網格數量的增加，計算時間也隨之增加，GPU的加速效果將越來越好，并行計算的優越性越明顯；直到加速至GPU的并行加速極限時，加速比趨于平穩。

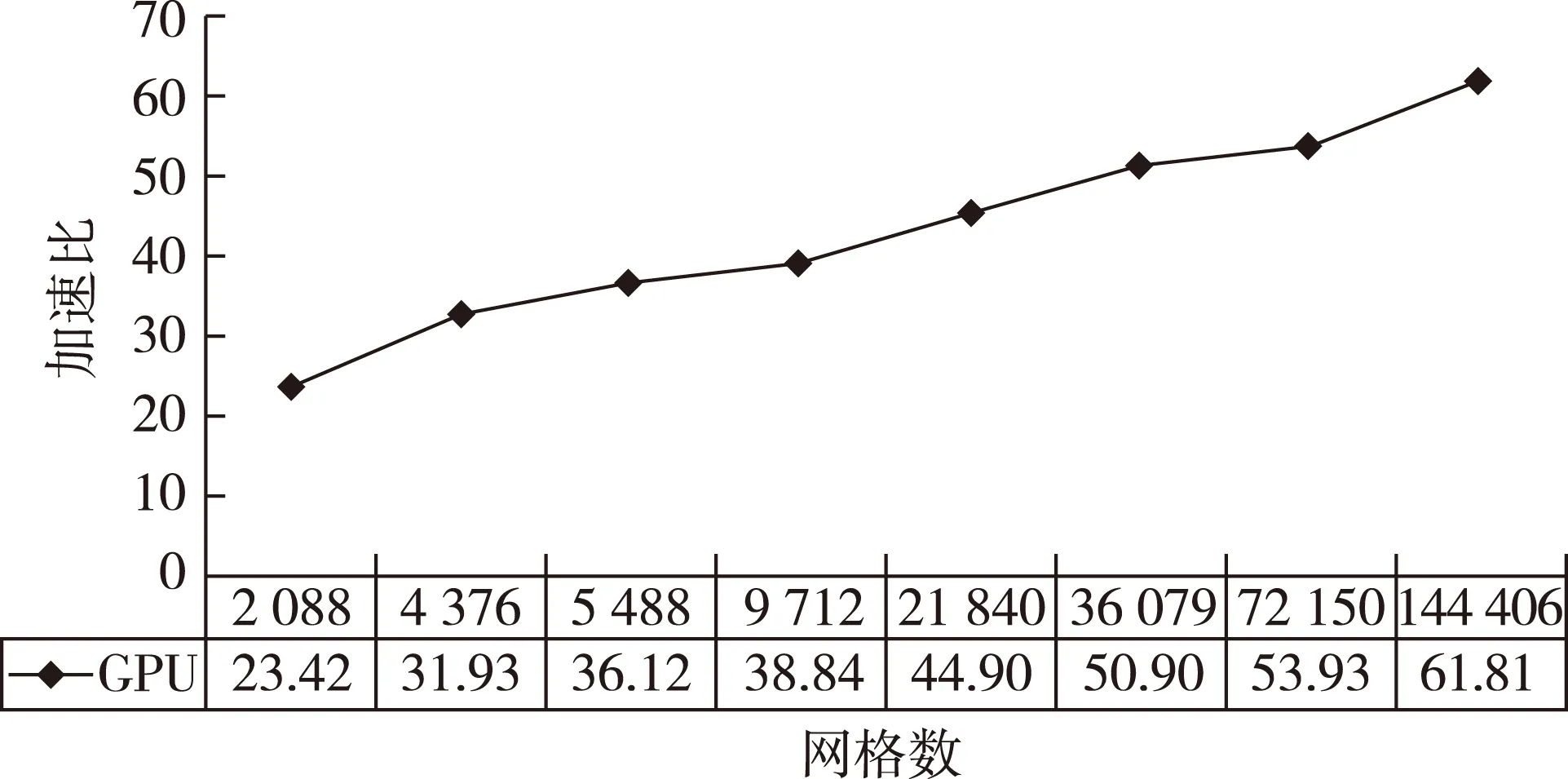
圖2　 GPU的加速比分析Fig.2　Analysis of speed-up ratio for GPU

4　結　論

(1) 在已有的條件模擬模型基礎上，針對三維實體模型的復雜性，提出分布式算法，改進了運算過程。

(2) 提出了基于GPU并行計算的并行條件模擬算法，將時間復雜度從O(n)降至O(logn)，并進行了儲量估算。

(3) 實驗結果表明，提出的并行條件模擬在估計精度不變或不下降的情況下具有很高的加速比與并行計算效率，適用于固體礦產儲量計算。

白樹仁，李濤，寧錦陽，2011. 基于MPI的并行Kriging空間降水插值[J]. 計算技術與自動化，30(1)：71-74.

李星，趙彥超，王國慶,2003. 條件模擬的原理及應用[J]. 地球學報, 24(增刊1)：226-228.

王仁鐸，胡光道，1988. 線性地質統計學[M]. 北京：地質出版社.

BROOKER P I, 1985. Two-dimensional simulation by turning bands[J]. Journal of the International Association for Mathematical Geology, 17(1): 81-90.

BOUDREAULT J P, DUBé J S, MARCOTTE D, 2016. Quantification and minimization of uncertainty by geostatistical simulations during the characterization of contaminated sites: 3-D approach to a multi-element contamination[J]. Geoderma, 264: 214-226.

DEAN S O,1995. Moving averages for Gaussian simulation in two and three dimensions[J]. Mathematical Geology, 27(8): 939-960.

HU H D, SHU H, 2015. An improved coarse-grained parallel algorithm for computational acceleration of ordinary Kriging interpolation[J]. Computers & Geosciences, 78(2): 44-52.JUANG K W, CHEN Y S, LEE D Y, 2004. Using sequential indicator simulation to assess the uncertainty of delineating heavy-metal contaminated soils[J]. Environmental Pollution, 127(2): 229-238.

LIANG M, MARCOTTE D, SHAMSIPOUR P, 2016. Simulation of non-linear coregionalization models by FFTMA[J]. Computers & Geosciences, 89(1): 220-231.

LIU L, WU C L, WANG Z B, 2016. Parallelization of the Kriging Algorithm in stochastic simulation with GPU accelerators[C]//BIAN F, XIE Y C. Geo-Informatics in Resource Management and Sustainable Ecosystem. Berlin: Springer, 197-205.

OLIVER D S, 1995. Moving averages for Gaussian simulation in two and three dimensions[J]. Mathematical Geology, 27(8): 939-960.

PESQUER L, CORTéS A, PONS X, 2011. Parallel ordinary Kriging interpolation incorporating automatic variogram fitting[J]. Computers & Geosciences, 37(4): 464-473.

PINHEIRO M, VALLEJOS J, MIRANDA T, et al., 2016. Geostatistical simulation to map the spatial heterogeneity of geomechanical parameters: A case study with rock mass rating[J]. Engineering Geology, 205: 93-103.

RIBEIRO S, CAINETA J COSTA A C, et al., 2016. Detection of inhomogeneities in precipitation time series in Portugal using direct sequential simulation[J]. Atmospheric Research, 171: 147-158.

SOJDEHEE M, RASA I, NEZAFATI N, et al., 2015. Probabilistic modeling of mineralized zones in Daralu copper deposit (SE Iran) using sequential indicator simulation[J]. Arabian Journal of Geosciences, 8(10): 8449-8459.

YAMAMOTO J K, LANDIM P M B, KIKUDA A T, et al., 2015. Post-processing of sequential indicator simulation realizations for modeling geologic bodies[J]. Computational Geosciences, 19(1): 257-266.

The parallel conditional simulation algorithm based on GPU and its application in reserve estimation

WANG Bingyi, DENG Weike, YU Xianchuan

(College of Information Science and Technology, Beijing Normal University, Beijing 100875, China)

Conditional simulation is a very time-consuming algorithm of three-dimensional high-precision interpolation. To solve the time-consuming problem in serial conditional simulation algorithm, we proposed a parallel conditional simulation algorithm based on GPU, and applied it to ore reserve estimation. First, this work conducted parallel analysis on the serial conditional simulation algorithm, and constructed CUDA general computing development environment based on the high parallelism of GPU. This realized the transformation of serial conditional simulation algorithm to parallel conditional simulation algorithm, and cut the time complexity of conditional simulation algorithm fromO(n) toO(logn). Experimental results of the Jiama copper deposit in Tibet on a computer with NVIDIA graphics demonstrated that, compared with the serial conditional algorithm, the GPU parallel conditional simulation algorithm could improve the efficiency by more than 60 times, without estimation accuracy loss.

conditional simulation; GPU; parallel computing; reserve estimation; Jiama copper deposit; Tibet

10.3969/j.issn.1674-3636.2016.03.507

2016-06-02；

2016-06-22；編輯：陳露

國土資源部公益性行業科研專項經費項目(201511079-02)，國家自然科學基金項目(41272359)，教育部博士點基金項目(20120003110032)

王冰怡(1995—)，女，碩士研究生，計算機軟件與理論專業，主要研究方向為空間信息數據處理與挖掘，E-mail：201521210034@mail.bnu.edu.com

P612; P628+.5

A

1674-3636(2016)03-0507-05