基于同步擾動隨機逼近的混合螢火蟲算法

李維剛，馮 寧，劉 超，劉 翱

（1.武漢科技大學信息科學與工程學院，湖北武漢，430081；2.武漢科技大學冶金工業過程系統科學湖北省重點實驗室，湖北武漢，430065；3.武漢科技大學管理學院，湖北武漢，430081；4.武漢科技大學智能信息處理與實時工業系統湖北省重點實驗室，湖北武漢，430065）

基于同步擾動隨機逼近的混合螢火蟲算法

李維剛1，2，馮 寧1，劉 超1，劉 翱2，3，4

（1.武漢科技大學信息科學與工程學院，湖北武漢，430081；2.武漢科技大學冶金工業過程系統科學湖北省重點實驗室，湖北武漢，430065；3.武漢科技大學管理學院，湖北武漢，430081；4.武漢科技大學智能信息處理與實時工業系統湖北省重點實驗室，湖北武漢，430065）

針對標準螢火蟲算法（FA）中存在的種群過早收斂、容易陷入局部最優等不足，提出一種以memetic算法為框架、將同步擾動隨機逼近和螢火蟲算法相結合的混合算法（FA-SPSA），即首先使用螢火蟲算法對種群進行全局尋優，然后使用同步擾動隨機逼近算法對選出的部分最優個體進行局部搜索，從而增強螢火蟲算法跳出局部最優解的能力。通過6個標準測試函數對FA-SPSA算法的性能進行檢驗，并與標準螢火蟲算法、果蠅算法、改進的果蠅算法等其他4種算法進行比較，結果表明，FA-SPSA算法在尋優精度、收斂速度、魯棒性等方面的性能總體上優于對比算法。

螢火蟲算法；同步擾動隨機逼近（SPSA）；memetic算法；全局搜索；局部搜索

螢火蟲算法（firefly algorithm，FA）［1］是一種新型智能優化算法，受螢火蟲發光相互吸引的現象啟發而設計。經過近幾年的發展，螢火蟲算法在理論和應用研究方面取得了較為豐富的成果，目前已在云計算調度［2］、路徑規劃［3］、PID控制器參數優化［4］、流水線調度［5］、鋼結構優化［6］等領域得到廣泛應用。

盡管螢火蟲算法及其改進算法可以解決一些復雜的優化問題，但是它仍然存在收斂過早、容易陷入局部最優、精度不夠高等問題，因此不少研究人員從改進位置更新公式和相對吸引度計算方法、自適應步長以及算法混合等諸多方面來彌補標準螢火蟲算法的不足。例如:針對大范圍搜索中尋優精度低、收斂速度慢等問題，白永珍［3］提出一種參數方差調節螢火蟲算法，通過計算種群亮度的方差評估種群的斂散性，根據優化的需要調節參數，從而解決了隨機搜索算法的收斂反彈問題，該算法在三維路徑規劃的實際應用中可以得到較好的優化解；針對PID控制器對復雜系統進行調節時會產生超調、震蕩等問題，李遠梅等［4］利用螢火蟲算法求出目標系統函數的最優值，對比用傳統Z-N算法計算得到的PID控制器參數值，該算法可以得到更好的解；張明等［7］在螢火蟲進化模式和搜索步長兩方面對算法進行改進，并與BP神經網絡相結合以平衡算法的收斂速度和精度，改進算法應用于5個標準測試函數，均得到了最優解。楊單等［8］提出在螢火蟲算法中加入混沌優化結果以改善個體之間的差異喪失，該混合算法可以解決云計算資源調度問題，并且具有較高的收斂速度。

本文提出一種以文化基因算法（memetic algorithm）為框架、將同步擾動隨機逼近和螢火蟲算法相結合的混合算法，該算法的主要思路為:采用螢火蟲算法對種群進行全局尋優，然后采用同步擾動隨機逼近算法對全局算法獲得的部分較優個體進行局部搜索，以增強螢火蟲算法跳出局部最優解的能力。本文最后通過6個標準測試函數對混合算法的尋優性能進行檢驗，并與其他幾種優化算法進行比較。

1　標準螢火蟲算法

考慮以下優化問題:

其中:f（X）為目標函數；X為決策變量；n為決策變量的個數；Lbi和Ubi分別為決策變量的下界和上界。

螢火蟲算法相關符號與定義如下:

（1）對于最大值優化問題，螢火蟲的發光亮度I與目標函數值f（X）之間的關系為［1］

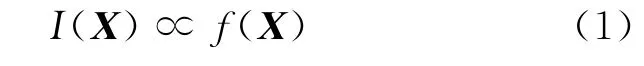
即二者成正比，螢火蟲的發光亮度越大，目標函數值就越好，而對于本文中的最小值問題，則恰好相反。

（2）螢火蟲的發光亮度I與距離r之間的關系為

式中:I0為r=0時螢火蟲自身的亮度；γ為光強吸收系數。

（3）吸引度β與距離r之間的關系為

式中:β0為r=0時的吸引度初始值。

（4）設螢火蟲i、j的位置為Xi、Xj，兩者之間的距離公式為

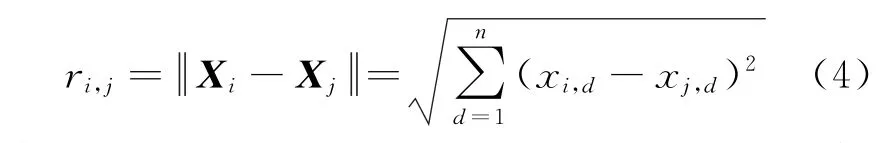
式中:d為空間維度；xi，d為螢火蟲i的空間坐標向量中的元素。

（5）位置更新函數為

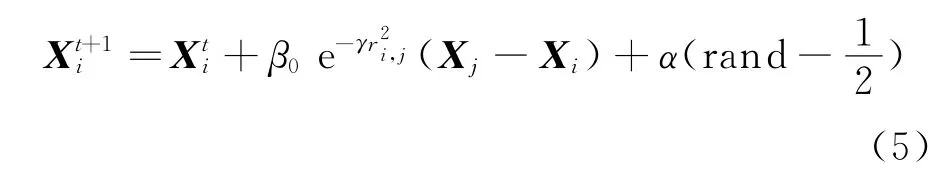
標準螢火蟲算法流程如下:

（1）輸入種群規模Popsize、最大進化次數Maxiter、參數β0和γ。

（2）隨機初始化螢火蟲種群Xi（i=1，2，…，n），計算發光亮度I（Xi），令進化次數iter=0。

（3）種群進化，其程序偽代碼為:

2　改進的混合螢火蟲算法

根據式（2）和式（3）可知，螢火蟲算法是根據螢火蟲的亮度來尋找函數最優值，而螢火蟲的亮度I（r）和吸引度β（r）都隨距離的增大而呈指數級減小，故距離較近的螢火蟲個體由于相對吸引度大而靠近，但距離較遠的個體相對吸引度就變得很小，同時由式（5）可知，標準螢火蟲算法的位置更新函數中只有一個隨機擾動項，所以該算法存在種群早熟、容易陷入局部最優等不足。

memetic算法是一種基于種群的全局搜索和基于個體的局部啟發式搜索的結合體，其實質是一種進化算法設計框架，通過組合不同的全局搜索算子和局部搜索算子可以構成不同的memetic算法。因此，針對標準螢火蟲算法的不足之處，本文根據memetic算法框架提出一種基于同步擾動隨機逼近（SPSA）的混合螢火蟲算法FASPSA，即采用螢火蟲算法進行全局搜索，得到m個最優個體，然后用同步擾動隨機逼近算法對這些個體進行局部搜索，以增強算法跳出局部最優解的能力。

2.1同步擾動隨機逼近

同步擾動隨機逼近是一種求解損失函數最優值問題的有效算法，通過同時擾動所有的待優化參數、再測量兩次損失函數的值就可以得到迭代過程中的逼近梯度。

在SPSA算法中，定義待優化的目標函數（即損失函數）為L（θ），梯度函數的逼近公式為

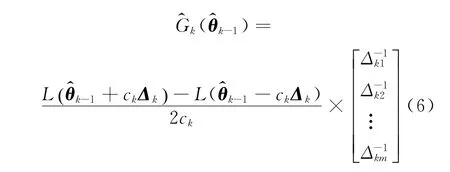
估計值θ的更新公式為

式中:ak=a/（A+k+1）α，其中，a、A、α均為系數。

2.2FA-SPSA算法流程

（1）確定算法參數:種群規模Popsize、最大進化次數Maxiter、運行的次數Runtime、亮度I0、吸引度β0、增益系數a和c，并初始化種群。

（2）利用標準螢火蟲算法對種群執行全局搜索，取出m個最優的螢火蟲個體。

（3）利用同步擾動隨機逼近算法對m個最優螢火蟲個體進行局部搜索:

a）生成同時擾動向量Δk；

b）產生兩個損失函數測量值L（θk-1+ckΔk）和L（θk-1-ckΔk）；

c）按式（6）進行梯度逼近；

d）按式（7）更新估計值。

3　算法驗證

3.1標準測試函數

為驗證FA-SPSA算法的尋優性能和收斂速度，本文選取6個標準測試函數（見表1）進行計算，并與標準螢火蟲算法（FA）和3種果蠅優化算法（FFO、FFO_LGMS、IFFO）［9］進行性能比較。

表1　標準測試函數［9］Table 1 Benchmark functions

3.2實驗環境

Window 7操作系統，CPU Inter（R）Core（TM）i5-2430M，主頻2.40 GHz，內存4 GB，編程語言為MATLAB 2012a。

3.3參數設置

為保證結果的公平性及客觀性，在測試中，FA和FA-SPSA算法中全局搜索部分采取相同參數:Popsize均分別取30和50，Maxiter=300，β0=1，γ=1。SPSA算法中的參數為:α=0.602，γ′=0.101［10］，最優螢火蟲個體數m=1，局部搜索允許的最大迭代次數為40；為了產生更小的擾動量，使函數在尋優過程中保持合適的搜索范圍，計算函數f3的增益系數取值為a=0.01、c=1，而計算其他5個函數的增益系數取值為a=0.1、c=1。

3.4結果分析

表2為5種不同算法用于6個標準測試函數（函數維度n=30）得到的平均值和標準差的尋優統計結果，其中:①FA和FA-SPSA算法分別獨立運行20次，種群規模為30，函數評價次數達到9000次終止進化；②FFO、FFO_LGMS、IFFO等3種算法的統計結果來源于文獻［9］，其最大函數評價次數為50 000。

從表2中可以看出，對于f1、f2、f4、f5、f6這5個函數，與其他4種算法相比，FA-SPSA算法具有更好的尋優性能:在標準測試函數的維度n為30時，FA-SPSA算法不僅優于標準螢火蟲算法，而且通過較少的函數評價次數獲得的結果要優于3種果蠅算法的結果，表現出更好的魯棒性和適應性。

對于測試函數f3，FA-SPSA算法比IFFO算法的優化精度低，比其他3種算法的優化精度高。但FA-SPSA算法以較少的計算代價找到了排名第二的較優解，其平均值和標準差與IFFO算法得到的最優結果相差不是很大，可推測在加大計算資源的條件下FA-SPSA算法將會找到更優解。

表2　5種算法的優化結果比較Table 2 Comparison of optimization results by five algorithms

表3為種群規模分別取30和50的情況下，FA和FA-SPSA算法在6個標準測試函數上的平均值和標準差的尋優統計結果，其中:每種算法分別獨立運行20次，種群規模為30時，函數評價次數達到9000次終止進化，種群規模為50時，函數評價次數達到15 000次終止進化。種群規模為30時，FA和FA-SPSA算法對于6個標準測試函數的優化收斂曲線如圖1所示，種群規模為50的優化收斂曲線與此類似。

結合表3和圖1可以看出:①種群規模增大時，FA和FA-SPSA的尋優精度和魯棒性都有一定提升；②與FA相比，FA-SPSA由于綜合了全局搜索和局部搜索的優點而具有更高的尋優精度；③FA-SPSA算法在經過2000～3000次函數評價后基本能找到最優解，收斂速度遠快于FA；④FA算法在進化一段時間后的收斂曲線變化緩慢，即在搜索過程中陷入了局部最優，而FASPSA因引入了梯度隨機變量擾動使算法能夠很快跳出局部最優而繼續尋找更優解。

圖1　FA和FA-SPSA對于標準測試函數的優化收斂曲線（Popsize=30）Fig.1 Convergence curves of FA and FA-SPSA on benchmark functions（Popsize=30）

綜上所述，相比其他幾種優化算法，特別是標準螢火蟲算法，FA-SPSA在尋優精度、收斂速度和魯棒性方面都占有優勢，因此利用memetic框架將螢火蟲算法和同步擾動隨機逼近算法結合在一起，十分有效地增強了混合算法的尋優能力。

4　結語

針對螢火蟲算法存在過早收斂、容易陷入局部最優、全局探索能力較弱、精度不夠高等問題，本文提出基于同步擾動隨機逼近的混合螢火蟲算法（FA-SPSA）。該算法采用螢火蟲算法執行全局搜索，采用同步擾動隨機逼近算法對部分已優化個體執行局部搜索，有效提高了算法跳出局部最優并進行全局探索的能力。從6個標準測試函數的對比實驗中可以看出，FA-SPSA算法在5個標準測試函數中找到最優解，在另外1個測試函數中找到了與最優解相差不大的次優解，總之，其在尋優精度、收斂速度、魯棒性方面表現出較優的性能。進一步的研究工作包括:①深入研究種群規模、吸引系數等參數對FA-SPSA尋優性能的影響；②考察FA-SPSA在多峰測試函數中的應用情況；③研究FA-SPSA在云計算調度、工程優化、車間調度等實際問題中的應用。

［1］Yang X S.Firefly algorithms for multimodal optimization［C］//Stochastic Algorithms:Foundations and Applications，SAGA 2009，Lecture Notes in Computer Science.Sapporo，Japan，October 26-28，2009，5792:169-178.

［2］李邐，姚曄，李鐵.基于改進型人工螢火蟲算法的云計算資源研究［J］.計算機應用研究，2013，30（8）:2298-2300.

［3］白永珍.基于參數方差調節螢火蟲算法的三維路徑規劃［J］.計算機系統應用，2015，24（5）:92-99.

［4］李遠梅，張宏立.基于改進螢火蟲算法PID控制器參數優化研究［J］.計算機仿真，2015，32（9）:356-359.

［5］李永林，葉春明.基于螢火蟲算法的零等待流水線調度優化［J］.機械設計與研究，2013，29（6）:50-54.

［7］張明，張樹群，雷兆宜.改進的螢火蟲算法在神經網絡中的應用［J/OL］.計算機工程與應用.（2015-12-03）［2016-01-05］.http://www.cnki.net/kcms/detail/11.2127.TP.20151202.0931.012.html.DOI: 10.3778/j.issn.1002-8331.1508-0134.

［8］楊單，李超鋒，楊健.基于改進混沌螢火蟲算法的云計算資源調度［J］.計算機工程，2015，41（2）: 17-20，25.

［9］Pan Q K，Sang H Y，Duan J H，et al.An improved fruit fly optimization algorithm for continuous function optimization problems［J］.Knowledge-Based Systems，2014，62（5）:69-83.

［10］Spall J C.Multivariate stochastic approximation using a simultaneous perturbation gradient approximation［J］.IEEE Transactions on Automatic Control，1992，37（3）:332-341.

［責任編輯 尚 晶］

Hybrid firefly algorithm based on simultaneous perturbation stochastic approximation

Li Weigang1，2，Feng Ning1，Liu Chao1，Liu Ao2，3，4
（1.College of Information Science and Engineering，Wuhan University of Science and Technology，Wuhan 430081，China；2.Hubei Province Key Laboratory of Systems Science in Metallurgical Process，Wuhan University of Science and Technology，Wuhan 430065，China；3.College of Management，Wuhan University of Science and Technology，Wuhan 430081，China；4.Hubei Province Key Laboratory of Intelligent Information Processing and Real-time Industrial System，Wuhan University of Science and Technology，Wuhan 430065，China）

To overcome such disadvantages as premature convergence and falling into local optimum easily in the basic firefly algorithm（FA），a hybrid algorithm named as FA-SPSA is presented，which introduces simultaneous perturbation stochastic approximation（SPSA）into FA under the frame of memetic algorithm.Firstly，FA is employed to search for global optimal solutions.Then SPSA is used in the local search aiming at the selected part of the best individuals，which enhances the ability of firefly algorithm to jump out of local optimum.The performances of FA-SPSA are testified by six benchmark functions and the calculation results are compared with those of basic firefly algorithm，fruit fly optimization and two improved fruit fly optimization algorithms，which indicates that FASPSA is generally superior to the other four algorithms in optimization accuracy，convergence speed and robustness.

firefly algorithm；SPSA；memetic algorithm；global search；local search

TP301.6

A

1674-3644（2016）05-0376-06

2016-03-30

湖北省教育廳科學技術研究計劃重點項目（D20161103）；武漢科技大學冶金工業過程系統科學湖北省重點實驗室開放基金資助項目（Z201501）；武漢科技大學智能信息處理與實時工業系統湖北省重點實驗室開放基金面上項目（2016znss18B）；武漢科技大學青年科技晨光計劃資助項目（2016070204010099）.

李維剛（1977-），男，武漢科技大學教授，博士.E-mail:liweigang.luck@foxmail.com

劉 翱（1987-），男，武漢科技大學講師，博士.E-mail:liuao@wust.edu.cn