基于直覺模糊集的時域證據組合方法研究

宋亞飛　王曉丹　雷蕾

基于直覺模糊集的時域證據組合方法研究

宋亞飛1王曉丹1雷蕾1

證據理論已廣泛應用于時空信息融合領域，由于時域信息融合表現出明顯的序貫性和動態性，為實現基于證據理論的時域信息融合，有效處理時域沖突信息，結合證據可靠性評估和證據折扣的思想，在直覺模糊框架內提出了一種基于復合可靠度的時域證據組合方法.首先定義一種基于可靠度的直覺模糊數排序方法，在此基礎上提出一種基于直覺模糊多屬性決策的證據可靠性評估方法；然后，基于此方法對時域信息序列中相鄰時間節點的證據可靠性進行評估，得到時域證據的相對可靠性因子；最后，結合由時域證據可靠度衰減模型得到的實時可靠性因子，得到時域證據的復合可靠性因子，再基于證據折扣運算和Dempster證據組合規則提出一種基于復合可靠度的時域證據組合方法.數值算例和仿真表明，該方法具有較強的時間敏感性，充分體現了時域信息融合的動態性特點，可以較好地處理時域證據中的沖突信息，基于該方法構建的融合識別系統具有較強的抗干擾能力.

證據理論，直覺模糊集，時域證據組合，可靠性評估，復合可靠度，證據折扣

引用格式宋亞飛，王曉丹，雷蕾.基于直覺模糊集的時域證據組合方法研究.自動化學報，2016，42（9）：1322-1338

證據理論最早由Dempster提出，后經Shafer對其進行完善和發展，所以又稱為Dempster-Shafer證據理論，或D-S證據理論［1-2］.證據理論中使用非精確概率對不確定性進行建模，相對于概率論中嚴格的公理化體系而言，證據理論滿足的公理化體系較為寬松，基于證據理論的推理不僅擺脫了對先驗概率的依賴，而且對自然語言中的模糊概念也有一定的處理能力，在不確定推理方面有很大優勢，可在一定程度上彌補貝葉斯推理方法的不足［3］.證據理論中，不確定性信息通過基本概率分配函數（Basic probability assignment function，BPAF）、信任函數（Belief function，BF）、似真函數（Plausibility function，PF）、眾信度函數（Commonality function，CF）等信任量化函數來描述，各量化函數均有明確的物理意義，且各量化函數之間存在對應關系.

在證據理論中，信度可以分配到辨識框架的所有子集，通過Dempster組合規則能夠對多個獨立的證據進行合成，可以對不確定信息進行有效融合，因此證據理論在不確定信息處理方面得到了廣泛的應用，證據理論中相關概念的物理意義及與其他不確定性理論之間的關系也引起了一些學者的興趣［3］.證據理論在實際應用中遇到的最大問題是沖突證據的組合問題，Zadeh首先指出Dempster組合規則在處理高沖突證據會產生錯誤的合成結果［4］，自此以后，Dempster組合規則飽受爭議，沖突證據的處理一度成為證據理論研究的熱點.國內外學者針對沖突證據的合成問題提出了許多改進方法［5-10］，主要包括基于沖突再分配的合成規則修訂以及基于證據折扣和加權平均的數據模型修訂兩大類.

目前大多數關于信息融合的研究都是在空域開展的，相關的融合方法也都是基于多傳感器信息融合系統提出的.然而，在信息融合中，受干擾信息和傳感器性能的影響，單個測量周期內各傳感器所獲取的信息并不一定準確，在信息融合中，往往還需要綜合利用多個時間節點的信息進行時域信息融合，因此信息融合應該是基于多傳感器的時空序貫融合的過程.在空域信息融合中，各傳感器所獲取的信息可以同時進行融合，沒有時間上的先后順序，而時域信息融合所處理的信息不是在同一時間獲取的，而是隨時間序列逐步獲取的；另外，時域信息融合系統一般對實時性有較高要求，不可能在各時間節點的識別信息全部獲取以后再進行融合，因此時域信息的融合具有明顯的序貫性、動態性和實時性，體現為融合結果的繼承和更新.

雖然基于證據理論的時域信息融合受到了一些研究者的關注，但目前仍缺乏有針對性的時域證據組合方法.Hong等［11］首先對基于證據理論的時空不確定信息融合模型進行了研究，以綜合目標識別為背景，提出了三種時空信息融合模型：遞歸集中式融合模型、遞歸分布無反饋融合模型和遞歸分布有反饋融合模型，對三種融合模型的特點進行了分析，但沒有給出具體的時域融合方法.洪昭藝等［12］對這三種融合模型進行了研究與改進，提出了一種混合式時空信息融合模型，在進行時域融合時直接運用Dempster規則進行證據組合.盡管部分學者基于遞歸集中式融合模型針對融合目標識別中的時空證據組合方法進行了研究［13-14］，但涉及到具體的時域證據組合方法時，有的直接利用空域證據組合方法［13］，不能反映時域信息序貫性的特點，時間因素對時域融合的作用不明顯；有的則是依據空域中各證據之間的相互關系來確定時域融合方法［15］，沒有充分利用時域信息之間的相互關系，不能很好地處理時域信息間的沖突.因此，時域證據組合方法還有待于進一步深入研究，需要基于時域信息融合的特點構建有針對性的時域證據組合方法.

本文面向時域信息融合對證據理論中的相關問題進行研究，從證據理論的相關研究中可知，證據組合的關鍵在于沖突信息的處理，證據可靠性評估是一種重要的沖突處理方法，時域證據組合的重點也在于如何處理證據間的沖突，因此，本文圍繞時域證據序列的動態可靠性評估展開研究.結合證據理論中的BPAF與直覺模糊集之間的關系，提出一種基于直覺模糊集的證據可靠性評估方法，以此為基礎對時域證據序列中相鄰證據間的相對可靠性進行評估，得到時域證據的相對可靠度；將前期研究中基于可靠度衰減模型提出的實時可靠度與相對可靠度結合，得到時域證據的復合可靠度，然后以復合可靠度為折扣因子，利用Shafer折扣準則對時域證據進行修正，最后利用Dempster組合規則進行證據組合.本文提出的時域證據組合方法充分考慮了時間因素對時域證據組合的影響，具有較強的動態性，而且對時域證據序列中的沖突證據也有較強的處理能力.

本文內容安排如下：第1節對證據理論相關知識進行簡要介紹，重點介紹證據理論中的基本概念、證據折扣運算、證據組合規則及證據理論中的決策規則；第2節回顧直覺模糊集相關知識，分析直覺模糊集與證據理論的關系；第3節基于直覺模糊數之間的排序提出一種基于直覺模糊多屬性決策的證據可靠性評估方法，為時域證據可靠性評估奠定基礎；第4節結合時域證據的實時可靠性因子和相對可靠性因子提出一種基于復合可靠度的時域證據組合方法；第5節對本文進行總結.

1　D-S證據理論

D-S證據理論的數學模型要求首先確立辨識框架，然后確定證據對每個集合的支持程度，再利用證據合成公式算出對所有命題的支持度.辨識框架是證據理論中進行證據建模和證據組合的基礎，也正是通過辨識框架將命題與集合對應起來，實現從抽象邏輯概念向直觀集合概念的轉化.在證據理論中，對于一個判決問題而言，其所有互不相容的結果組成的完備集合Θ=｛θ1，θ2，···，θn｝稱為辨識框架.由辨識框架Θ的所有子集組成Θ的冪集，記作2Θ，它的基數為2|Θ|，證據理論是基于辨識框架用集合來表示命題的.

1.1基本概念

辨識框架Θ確定以后，可以根據可用信息對其命題所對應的子集賦予相應的信任度，具體表現為基本概率分配函數、信任函數、似真函數等信任量化函數，這些函數分別從不同角度對信任度進行量化，各函數之間均存在對應關系，通過其中一個函數可以同時獲取其他所有函數.下面對證據理論中的幾種信任量化函數進行說明.

設Θ=｛θ1，θ2，···，θn｝為辨識框架，若函數m：2Θ→［0，1］滿足：1）m（?）=0；2）?A?Θ，0≤m（A）≤1；3）∑A?Θm（A）=1.則稱之為基本概率分配函數（BPAF）.

基本概率分配函數也稱為基本信任分配函數（Basic belief assignment function，BBAF）或mass函數.由于基本概率分配函數反映了證據對各子集的支持程度，通常將BPAF與證據對應起來.?A?Θ，m（A）稱為A的基本概率質量（Basic probability mass，BPM），表示證據對命題A的支持度.

對于辨識框架Θ=｛θ1，θ2，···，θn｝上的基本概率分配函數m，?A?Θ，若m（A）＞0，則稱A為m的焦元.如果|A|=1，則A為單元素焦元；若|A|≥2，則A為復合焦元.所有焦元的并集稱為m的核（Core），記為C，并稱m聚焦在C上.如果m的焦元均為辨識框架Θ的單元素子集，那么退化為Bayesian基本概率分配，與Θ上的概率分布函數有相同的數學形式.

設m為辨識框架Θ=｛θ1，θ2，···，θn｝上的基本概率分配函數，與之對應的信任函數表示為Bel：2Θ→［0，1］，滿足Bel（?）=0，?A?Θ且A/=?，有Bel（A）=∑X?Am（X），Bel（A）的數值表示證據對A為真的信任程度.與m對應的似真函數定義為函數Pl：2Θ→［0，1］，滿足?A?Θ，有Pl（A）=，Pl（A）的取值稱為A的似真度，表示了A為非假的信任度.

Bel（A）和Pl（A）分別代表了證據對A的支持度的最小值和最大值，通常用［Bel（A），Pl（A）］來表示A的信任度區間，Pl（A）-Bel（A）在某種程度上反映了A的不確定程度.

定義1.Shafer折扣準則［2］.若辨識框架Θ=｛θ1，θ2，···，θn｝上的基本概率分配函數m對應的證據源不完全可靠，且該證據源的可靠性因子為λ，λ∈［0，1］，則可通過Shafer折扣準則對m進行折扣運算，折扣后的證據表示為

可以看出，經過證據折扣后，mλ中Θ獲得的基本概率質量增加，其他焦元的基本概率質量則減小，Shafer折扣準則將證據源不可靠性帶來的影響轉化為mλ中完全未知的部分，而且可靠性因子取值越接近0，折扣后的BPAF的不確定性越大.Shafer折扣準則對研究沖突證據的組合具有重要意義.

1.2證據組合規則

在多源信息系統中，多個證據源分別獲得BPAF m1，m2，···，mp，或同一證據源在不同時刻分別獲得BPAF mt1，mt2，···，mtr，則多個BPAF組合后可以得到一個新的BPAF，這一過程在證據理論中表現為證據的動態更新.

定義2.Dempster組合規則［1］.設m1和m2是辨識框架Θ=｛θ1，θ2，···，θn｝上兩個相互獨立的基本概率分配函數，二者組合后得到新的BPAF為m=m1⊕m2，簡記為m1⊕2，對?A?Θ滿足

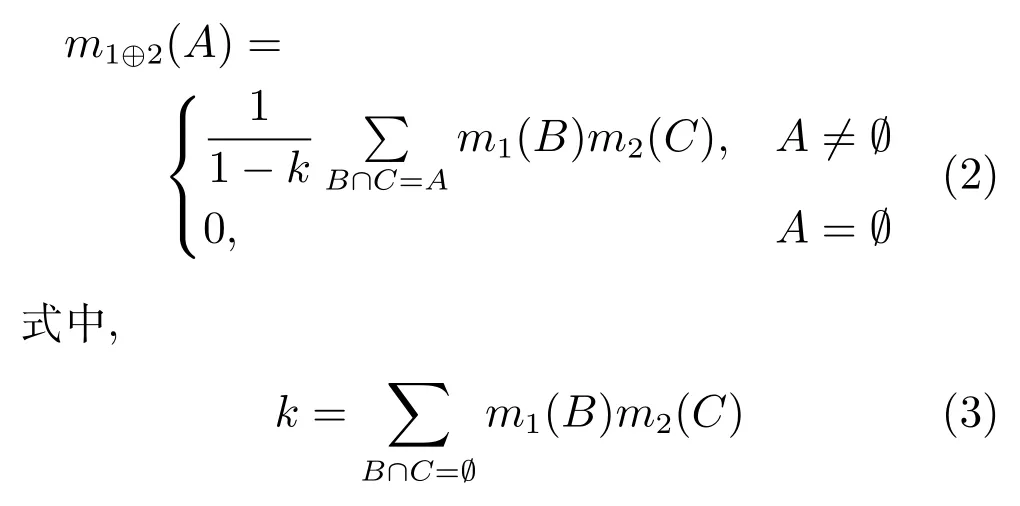
表示兩證據間的沖突度，k=1表示m1和m2完全沖突，二者不能通過Dempster組合規則進行組合.

Dempster組合規則可以推廣到多組證據組合的情形，Dempster證據組合規則滿足交換律和結合律，這為多個證據的組合提供了方便，既可以串行計算，將各個證據依次組合；也可以并行處理，將若干個證據分別合成，然后再將它們的合成結果進行組合.而且，對若干個相同的證據進行組合時，Dempster規則表現出較強的聚焦性，即元素少的焦元的基本概率質量會增加，元素多的焦元的基本概率質量會減少，而且證據數量越大該現象越明顯.

1.3證據理論中的決策

Dempster-Shafer證據理論中用來量化信任的主要函數（基本概率分配函數、信任函數以及似真函數），分別從不同角度對辨識框架中各子集的信任度進行度量，進行最終決策時，可以分別或共同使用這些函數進行決策，也可以將它們轉化為辨識框架上的概率分布后再進行決策.盡管基于信任度量函數進行決策的方法對實際的決策問題具有一定的指導作用，但這些方法難以給出具體的決策結果，因為這些方法都是直接基于證據焦元設計的，在存在復合焦元或各焦元之間存在共同元素的情況下，得到的決策結果具有太大的不確定性，不利于最終的決策.只有將基本概率分配函數轉換為辨識框架上的概率分布函數才能從根本上對決策進行指導，依據辨識框架中每一個單元素子集的概率函數，可以利用最大概率準則直接進行決策，或進一步結合效用函數或損失函數進行決策.將基本概率分配函數轉化為概率的過程稱為BPAF概率轉換，或貝葉斯轉換.雖然多種BPAF概率方法已相繼被研究者們提出［15］，但Pignistic概率轉換方法在決策中的應用最為廣泛，Pignistic概率轉換方法可表述如下.

定義3.Pignistic概率轉換［16］.對辨識框架Θ=｛θ1，θ2，···，θn｝上的BPAF m，?A?Θ，其Pignistic概率轉換定義為

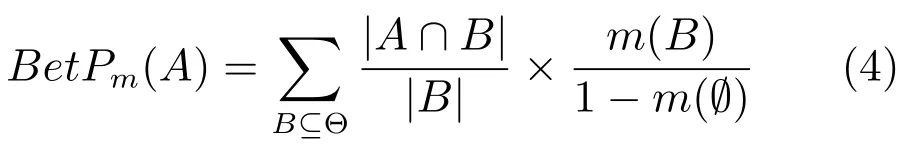
式中，BetPm（·）稱為Pignistic概率函數，在數學形式上與一般的概率函數相同.

特別地，對于單元素子集而言，?θ∈Θ，｛θ｝的Pignistic概率為

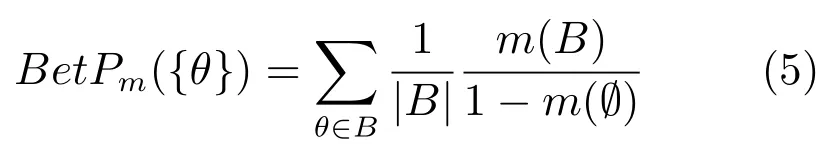
2　直覺模糊集與證據理論

2.1直覺模糊集相關概念

在經典集合論中，對于論域中的任何一個元素（對象），它與該論域中集合之間的關系只能是屬于或不屬于，即一個元素（對象）是否屬于某一集合的特征函數的值域為0和1兩個數，這種二值邏輯為現代數學的發展奠定了基礎.而Zadeh模糊集的核心思想在于把特征函數的值域擴展到閉區間［0，1］上，稱其為隸屬度函數，而把取定的值稱為元素相對于集合的隸屬度.

定義4.模糊集［17］.設X=｛x1，x2，···，xn｝為非空論域，X上的模糊集（Fuzzy set，FS）A定義為

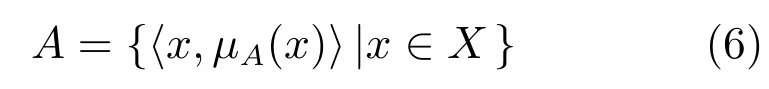
其中，μA（x）：X→［0，1］為隸屬度函數，表示x屬于A的程度.

論域X上的所有模糊集可表示為FSs（X）.在模糊集中，vA（x）=1-μA（x）為x相對于A的非隸屬度函數，因此，x與A的關系完全是由隸屬度來刻畫的，μA（x）越接近于1，表示x屬于模糊集A的程度越高；μA（x）越接近于0，表示x屬于模糊集A的程度越低；當μA（x）∈｛0，1｝時，A退化為經典集合，相對于模糊集而言，經典集合也稱為精確集（Crisp set，CS）.因此，模糊集可以看作是經典集合的推廣，而精確集則是特殊的模糊集.

為了更好地對不確定性信息進行表述和建模，Atanassov提出了直覺模糊集的概念.

定義5.直覺模糊集［18］.設X=｛x1，x2，···，xn｝為非空論域，X上的直覺模糊集（Intuitionistic fuzzy set，IFS）A定義為

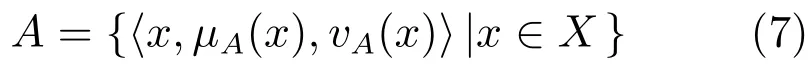
其中，μA（x）：X→［0，1］和vA（x）：X→［0，1］分別為x相對于A的隸屬度函數和非隸屬度函數，且滿足

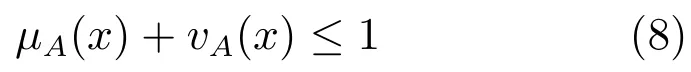
在直覺模糊集中，由隸屬度與非隸屬度函數的和不大于1可以導出另一個參數，即猶豫度函數πA（x）：X→［0，1］，x相對于A的猶豫度函數表示為

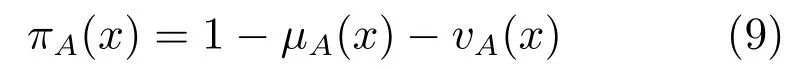
為方便表述后文，用IFSs（X）表示論域X中所有直覺模糊集；單元素論域X=｛x｝中的直覺模糊集可以簡記為〈μA（x），vA（x）〉或〈μA，vA〉，A=〈μA，vA〉也常用來表示一個直覺模糊數（Intuitionistic fuzzy value，IFV）.

需要說明的是，除了定義5，直覺模糊集還有其他表述方式，已有研究表明，直覺模糊集與Vague集是等價的［19］，而且也可以用區間的形式表述［20］，直覺模糊集〈μA（x），vA（x）〉可以用區間［μA（x），1-vA（x）］表示，μA（x）和1-vA（x）分別表示x屬于A的隸屬度的下界和上界，這與區間值模糊集的表述方式相似，因此直覺模糊集與區間值模糊集之間可以互相轉化.而且，在證據理論中曾用區間［Bel（A），Pl（A）］表示命題的信任度區間，這與直覺模糊集的區間表示方法很接近.后文將基于此對證據理論與直覺模糊集之間的關系進行分析.

對于直覺模糊集A，當πA（x）=0時，vA（x）= 1-μA（x），直覺模糊集A退化為Zadeh的模糊集.因此，模糊集可以看作是特殊的直覺模糊集，同樣，精確集也是直覺模糊集的一個特例.由此可見，精確集和模糊集都可以在直覺模糊框架內統一表示.

設A為論域X=｛x1，x2，···，xn｝中的任意非空精確子集，即A?X且A/=?，那么A可以表示為直覺模糊集，其中，若x∈A，則；否則，

例如，論域X=｛x1，x2，x3，x4｝中的子集和B=｛x1，x2，x3｝可分別表示為直覺模糊集.

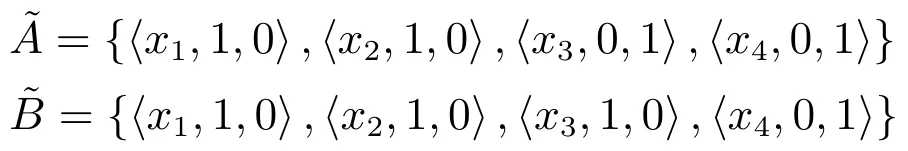
精確集、模糊集、直覺模糊集在形式上的統一進一步表明了直覺模糊集在信息表述方面的靈活性，在直覺模糊集框架內，可以對各種不確定信息進行統一建模.

2.2直覺模糊集與BPAF之間的關系

近年來，越來越多的學者開始關注直覺模糊集與證據理論之間的關系.例如，Li等［21］從Vague集的角度分析證據理論，認為證據理論是一種特殊的Vague集，并利用Vague集之間相似度的概念討論了BPAF之間的相似程度問題，由于Vague集與直覺模糊集是等價的，因此，從這個意義上講，證據理論也是直覺模糊集的特例；文獻［22］和文獻［23］從證據理論的角度對直覺模糊集中的相關概念進行了解釋，并提出了基于證據理論的直覺模糊數排序方法和決策規則；Yager［24］則直接從直覺模糊集的角度對證據理論進行研究；文獻［25］通過定義廣義信任函數和廣義似真函數來確定直覺模糊集中的隸屬度與非隸屬度函數.下面進一步分析證據理論中的BPAF與直覺模糊集之間的關系.

從集合論的角度來看，證據理論中的辨識框架對應于直覺模糊理論中的論域，若將證據理論中辨識框架Θ=｛θ1，θ2，···，θn｝上的基本概率分配函數m看作是論域Θ=｛θ1，θ2，···，θn｝上的直覺模糊集M，那么對于Θ中的元素θi而言，信任函數Bel（θi）表示θi∈M的隸屬度，Bel（ˉθi）即1-Pl（θi）表示θi相對于直覺模糊集M的非隸屬度.通過該方法，可以將基本概率分配函數的焦元進行簡化，全部聚焦在單元素焦元上，每個焦元的信任度為直覺模糊數〈Bel（θi），1-Pl（θi）〉，此外，直覺模糊數〈Bel（θi），1-Pl（θi）〉也可以看作是對象θi與判決問題真實解之間的匹配程度，例如在目標識別中，〈Bel（θi），1-Pl（θi）〉可以表示目標θi與真實目標之間的匹配程度.

另一方面，定義在論域X=｛x｝上的直覺模糊集A=〈x，μA（x），vA（x）〉可以看作是對問題“x是否屬于A”的回答，在該問題中，辨識框架為Θ=｛Y es，No｝，根據隸屬度函數和非隸屬度函數的意義可得m（｛Y es｝）=μA，m（｛No｝）=vA，m（Θ）=πA.因此A=〈x，μA（x），vA（x）〉對應于一個二分支持函數m，表示為

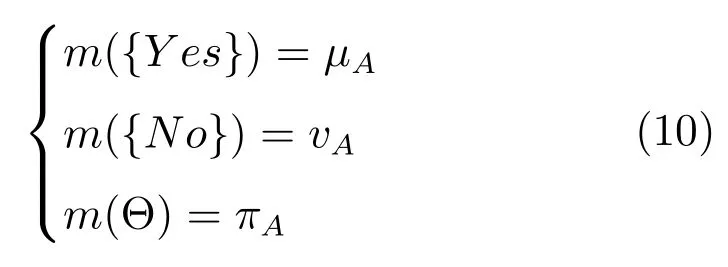
顯然，該轉換關系可以推廣到任意論域上的直覺模糊集.因此，可以在證據理論框架內對直覺模糊集之間的運算規則以及直覺模糊測度進行研究.需要說明的是，從證據理論到直覺模糊集的轉換會帶來一定的信息損失，而且基本概率分配函數與直覺模糊集之間不是一一對應的.

3　直覺模糊框架內的證據可靠性評估

為削弱不可靠信息對融合結果的影響，在進行證據組合前需要對證據源的可靠性進行評估，這也是處理高沖突證據的一種有效方法.近些年，國內外學者在證據可靠性評估方面做了大量工作［26-29］，在傳感器靜態可靠性評估中，需要利用已知訓練樣本獲得傳感器的固有屬性信息，然而，在信息融合實際中，先驗信息總是非常有限的，因此，在大多數情況下，靜態可靠性的評估帶有較強的不確定性.而且，在工程應用中，傳感器的工作環境可能會發生變化，傳感器的性能與其工作環境密切相關，諸如人為干擾、惡劣天氣等因素都會使傳感器的可靠度降低，甚至使其失效.所以傳感器靜態可靠性評估方法具有一定的局限性，不能滿足工程實際的需求.對于基于證據理論的信息融合系統而言，證據的可靠性評估更多的是基于傳感器實時輸出的動態可靠性評估.

現有的證據動態可靠性評估大都是基于“大多數原則”開展的，在多個傳感器提供的證據中，如果某個證據被其他大多數證據都支持，那么可以認為該證據的可靠度較高；對于兩個證據而言，如果它們之間存在較大的沖突，那么至少有一個是不可靠的［26］.所以，證據動態可靠性評估大都是基于證據間的沖突度量和距離度量進行的，這類證據動態可靠性的評估方法最終都歸結為證據沖突度量和距離度量的定義問題，而證據沖突度量問題依然未能很好地解決，不同的沖突度量標準可能會得到不同的評估結果.而且，當只有兩個證據時，通過以上方法得到兩個證據的可靠性因子均為1，與具體的BPAF無關，即使二者之間存在較大沖突，根據相等的可靠性因子無法確定哪一個證據不可靠，因此基于“大多數原則”的可靠性評估方法不適用于只有兩個證據的情況，無法利用此類方法對時域證據序列中相鄰兩個證據的可靠性進行評估.為了對證據的動態可靠性進行全面客觀的評估，更好地適應時域證據可靠性評估的需要，本節將提出一種基于直覺模糊多屬性決策（Intuitionistic fuzzy multiple criteria decision making，IFMCDM）的證據動態可靠性評估方法.

3.1基于可能度的直覺模糊數排序

定義6.基于可能度的區間數排序［30］.設兩個區間數分別為α=［aL，aU］和β=［bL，bU］，滿足aL≤aU，bL≤bU，那么α不小于β的可能度P（α≥β）可定義為

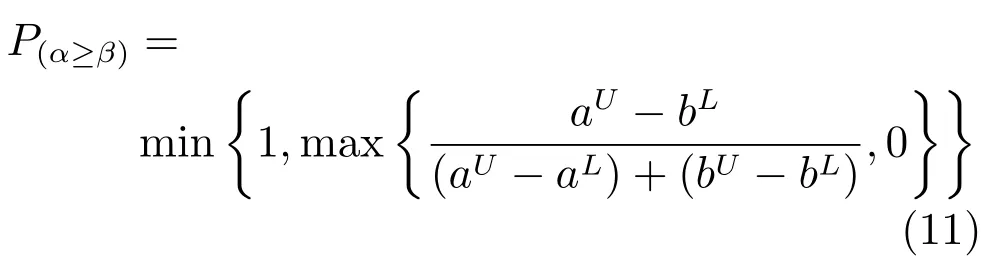
當aL=aU=a，bL=bU=b同時成立時，分母為零，式（11）不再適用.此時，α和β退化為精確的實數，因此有a＞b?P（α≥β）=1，a＜b?P（α≥β）=0，a=b?P（α≥β）=0.5.

對于區間數α=［aL，aU］和β=［bL，bU］，α不小于β的可能度P（α≥β）滿足下列性質：

1）0≤P（α≥β）≤1；

2）P（α≥α）=0.5；

3）P（α≥β）=1?aL≥bU；

4）P（α≥β）+P（β≥α）=1.

由于直覺模糊數A=〈μA，vA〉和B=〈μB，vB〉可分別表示為區間數的形式A=［μA，1-vA］和B =［μB，1-vB］，于是，基于區間數間的排序規則，可對A、B進行排序.

定義7.基于可能度的直覺模糊數排序.A=〈μA，vA〉和B=〈μB，vB〉為兩個直覺模糊數，其中πA和πB不同時為零，那么A≥B的可能度P（A≥B）定義為

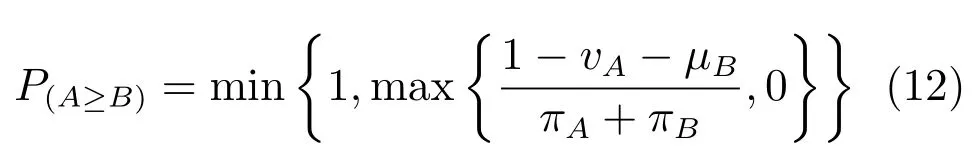
當πA和πB同時為零時，A和B都表示精確數，于是有μA＞μB?P（A≥B）=1，μA＜μB?P（A≥B）=0，μA=μB?P（A≥B）=0.5.

對于兩個直覺模糊數A=〈μA，vA〉和B=〈μB，vB〉，P（A≥B）滿足以下性質：

1）0≤P（A≥B）≤1；

2）P（A≥A）=0.5；

3）P（A≥B）=1?μA≥1-vB；

4）P（A≥B）+P（B≥A）=1.

值得注意的是，根據性質3）可得P（A≥B）=1?μA≥1-vB，由1-vA≥μA，1-vB≥μB，可得1 -vA≥μA≥1-vB≥μB，由此可進一步得到μA≥μB，vA≤vB，即P（A≥B）=1?μA≥μB，vA≤vB，但其逆命題不成立.

假設有N個直覺模糊數A1，A2，···，AN，表示為Ai=〈μAi，vAi〉，i=1，2，···，N，那么根據定義7中的排序規則可對N個直覺模糊數進行排序，過程如下：

1）計算Ai≥Aj的可能度.

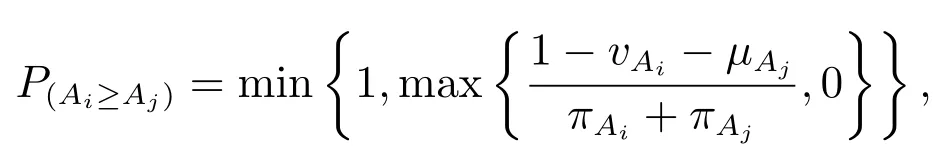
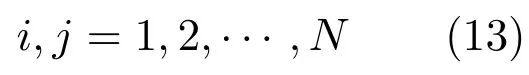
為簡化表述，可令Pij=P（Ai≥Aj）.

2）構造N個直覺模糊數之間的對比關系矩陣.

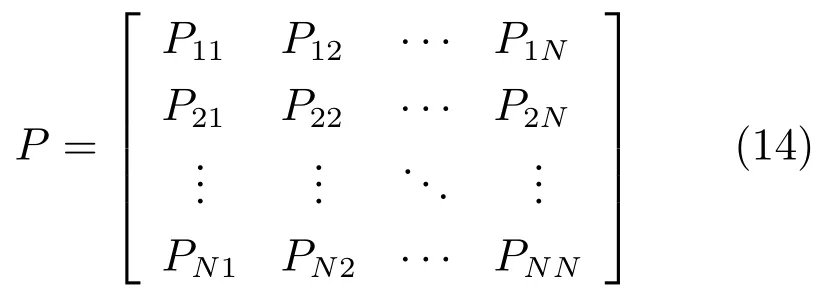
顯然，P滿足?i，j∈｛1，2，···，N｝，0≤Pij≤1，Pij+Pji=1，Pii=0.5.

3）計算矩陣P中每一行中所有元素的和，可以得到

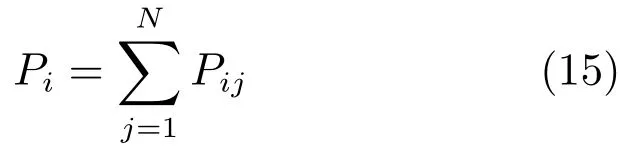
4）由于Pi反映了Ai不小于其他元素的可能度，即Pi≥Pj?Ai≥Aj.因此，可以根據Pi的大小順序對A1，A2，···，An進行排序.

該排序方法的具體實施過程，如例1所示.

例1.已知三個直覺模糊數分別為A1=〈0.6，0.3〉，A2=〈0.45，0.2〉，A3=〈0.5，0.25〉.

A1、A2和A3之間基于可能度的對比關系矩陣為

計算行和可得

由于P1＞P2＞P3，因此A1、A2和A3的排序結果為A1＞A2＞A3.

3.2基于IFMCDM的證據可靠性評估

設A=｛A1，A2，···，Am｝為方案集，X=｛x1，x2，···，xn｝為屬性集，方案Ai在屬性xj下的評估結果表示為直覺模糊數〈μij，vij〉，i=1，2，···，m；j =1，2，···，n.〈μij，vij〉也可認為是方案Ai在屬性xj下滿足理想方案的程度.直覺模糊多屬性決策模型表述為A在X上的決策矩陣：

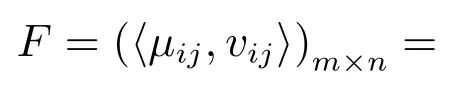
根據前面的介紹，可以將辨識框架Θ=｛θ1，θ2，···，θn｝上的BPAF m轉化為直覺模糊集，直覺模糊數〈Bel（θi），1-Pl（θi）〉可以看作該證據對θi的支持度.在基于證據理論的目標融合識別系統中，每個傳感器以BPAF的形式給出對待識別目標身份的識別信息，通常每個傳感器反映了目標的不同屬性，對于傳感器Sk提供的BPAF m而言，〈Bel（θi），1 -Pl（θi）〉可以視為θi在屬性Sk下滿足待識別目標真實類別的程度，從這個意義上講，證據組合問題與直覺模糊多屬性決策是等價的.

設Θ=｛θ1，θ2，···，θp｝為辨識框架，q個待組合證據對應的BPA為m1，m2，···，mq，Suij=〈μj（θi），vj（θi）〉是mj對θi的支持度，其中μj（Ai）= Belj（Ai），vj（Ai）=1-Plj（Ai），i=1，2，···，p；j =1，2，···，q.那么，該證據組合問題等價于如式（17）所示的直覺模糊多屬性決策模型.

因此，證據組合問題就轉化為多屬性條件下的方案評估問題，各個證據的動態可靠性等價于多屬性決策中各屬性的權重，接下來，將提出一種基于IFMCDM的證據動態可靠性評估方法.

將證據組合問題轉化為直覺模糊多屬性決策問題以后，可以利用直覺模糊多屬性決策中屬性權重的估計方法來對證據動態可靠性進行評估，盡管相關學者提出了大量屬性權重確定方法，但這些方法大都是基于有序加權平均運算（Ordered weighted averaging，OWA）和非線性優化模型開展的，有的還需要先驗信息來提供所謂的理想方案.顯然，這些方法并不適用于缺乏先驗知識條件下的證據動態可靠性評估.因此，我們提出一種基于自我評估的證據動態可靠性評估方法.

在多屬性決策中，已知各個備選方案在各屬性下的評估結果，如果假設每一種方案為獨立的“經濟人”，由于“經濟人”的顯著特點在于追逐最大利益，因此每一個“經濟人”（方案）會將最大的權重賦給那些最支持它的屬性.例如對于方案Ai而言，在屬性xj下的評估結果為〈μij，vij〉，如果〈μik，vik〉= max｛〈μij，vij〉｝，那么Ai會給xk賦予最大的權重，但是這會帶來另外一個問題，即每一個方案把所有的權重都分配給最支持它的屬性，即Ai會給xk賦予權重1，其他各屬性的權重為0，這將會帶來極大的信息損失，并不利于最終的決策.我們需要既能夠尊重最大評估結果所對應的屬性xk的優先地位，又要充分利用各屬性下的評估結果.因此，我們可以借助基于可能度的直覺模糊數排序方法構建一種屬性權重估計方法，進而實現證據動態可靠性評估.

方案Ai在屬性xj下的評估結果為〈μij，vij〉，i =1，2，···，p；j=1，2，···，q，對于任意兩個屬性xj和xk下的評估結果〈μij，vij〉和〈μik，vik〉，可以設為〈μij，vij〉大于〈μik，vik〉的可能度，那么

據此可以構建q個直覺模糊數之間的對比關系矩陣P（i）

矩陣P（i）第k行的和可以作為xk大于其他各屬性的可能度，于是有

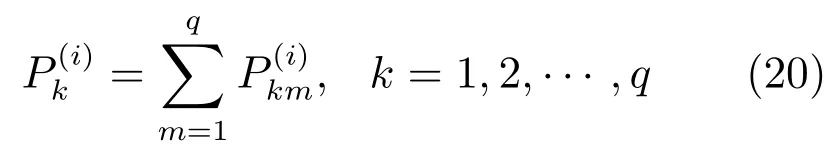
根據“經濟人”的假設，最好的評估結果對應的屬性應該被賦予最大的權重系數，因此，方案Ai對屬性xj賦予的權重可表示為

最終可以得到依據方案Ai獲得的屬性權重向量

由于各個屬性的權重是每個方案根據其在各個屬性下的評價結果而得到的，因此該方法也稱為自主評價法.然而不難發現，各個方案對賦予每個屬性的權重系數不盡相同，因此需要確定最終的權重系數.在此，可以借鑒群決策的思想，將每個方案提供的權重向量視為不同專家對屬性權重做出的決策，可以假設最終的理想權重向量與所有之間的夾角之和最小.可以運用特征根法來求解理想權重向量，設矩陣，那么方陣WWT的最大特征值所對應的特征向量 www（Perron-Frobenius向量）即為理想權重向量.由于同一特征值對應的特征向量并不唯一，因此需要將w進行歸一化

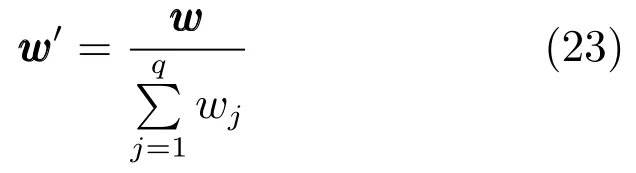
最終，基于證據動態可靠性與屬性權重之間的關系，可以得到證據的動態可靠性因子，但是在證據動態可靠性評估中，通常令最可靠的證據的可靠度為1，因此歸一化的證據動態可靠性因子可表示為

以上證據可靠性評估方法稱為基于直覺模糊多屬性決策的證據可靠性評估（Evidence reliability evaluation based on IFMCDM，ERE-IFMCDM）.

4　基于復合可靠度的時域證據組合方法

文獻［31］對時域證據融合中的可信度衰減模型進行了研究，提出了基于實時可靠度的時域證據序貫組合方法，時域證據的實時可靠性因子定義如下.

定義8.實時可靠性因子（Real-time reliability factor，RTRF）.系統在tj時刻所獲取的BPAF mj在時刻ti（ti＞tj）的實時可靠性因子為

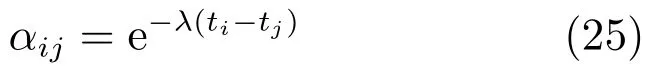
其中，λ＞0為可靠度衰減因子，為減小信息損失，λ的取值范圍為0＜λ＜ln2.

為便于表述，當前時刻k記為tk，前一時刻k -1記為tk-1，各時刻的證據對應的BPAF為mk和mk-1，根據可靠度衰減模型可知，前一時刻的累積融合結果mk-1在當前時刻的可靠性因子為α= e-λ（tk-tk-1），因此當前時刻需要考慮的兩個BPAF為mk-1折扣后的BPAF和當前時刻各傳感器的融合結果mk.

時域證據融合的關鍵在于如何處理當前獲得的最新證據mk與前一時刻累積結果mk-1之間的沖突，雖然文獻［31］提出的可靠度衰減模型可以用于沖突證據的組合，但在計算證據可靠度只利用了時域信息本身的時效性，與各時間節點的證據對應的BPAF無關，而且沒有考慮mk與mk-1之間的相互關系，因此單純依靠可信度衰減模型進行時域證據組合不夠全面.為進一步增強時域融合算法對沖突信息的處理能力，本節將在直覺模糊框架內對mk和mk-1的相對可靠性進行評估，結合實時可靠性因子得到兩個相鄰時間節點間證據的復合可靠度，進而確定折扣因子，實現時域沖突信息的有效融合.

4.1證據相對可靠性評估

根據第3節關于證據可靠性評估的論述可知，基于證據距離的可靠性評估并不能用來對m（k）和m（k-1）的可靠性進行評估，因為在只有兩個證據的情況下，最終的評估結果為兩個證據的可靠性都為1，無法對證據源進行折扣.基于直覺模糊多屬性決策模型的證據動態可靠性評估方法擺脫了對證據距離度量的依賴，可用于對兩個證據的動態可靠性進行評估，因此可以基于此方法對時域證據m（k）和m（k-1）的可靠性進行評估，其主要目的在于通過可靠性評估，綜合分析m（k）和m（k-1）在對當前時刻融合結果的影響程度.

設辨識框架為Θ=｛θ1，θ2，···，θn｝，根據基于IFMCDM的證據動態可靠性評估方法，可以按如下流程對相鄰時間節點間的證據進行可靠性評估.

1）根據可靠度衰減模型，計算mk-1在當前時刻的可靠度因子α：

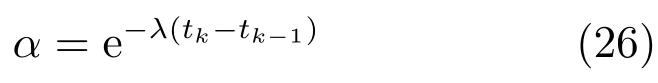
2）按照Shafer折扣準則，對mk-1進行折扣運算，折扣后的BPAF為mαk-1：

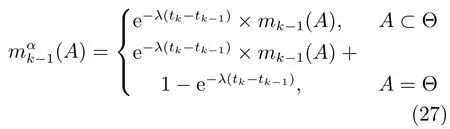
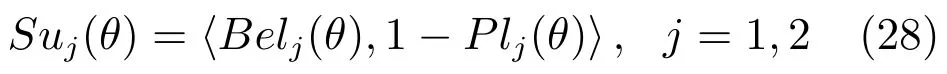
5）根據基于可能度的直覺模糊數排序規則，在θi（i=1，2，···，n）的條件下計算Su1（θi）大于Su2（θi）的可能度為

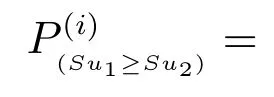
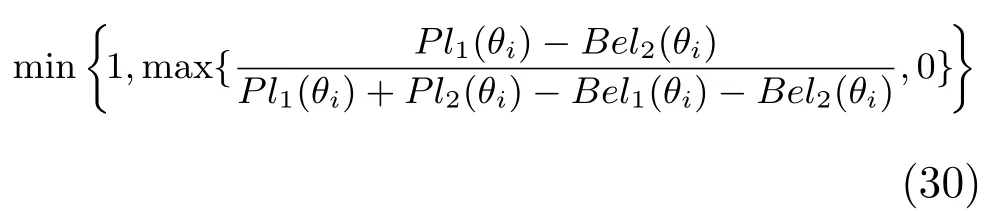
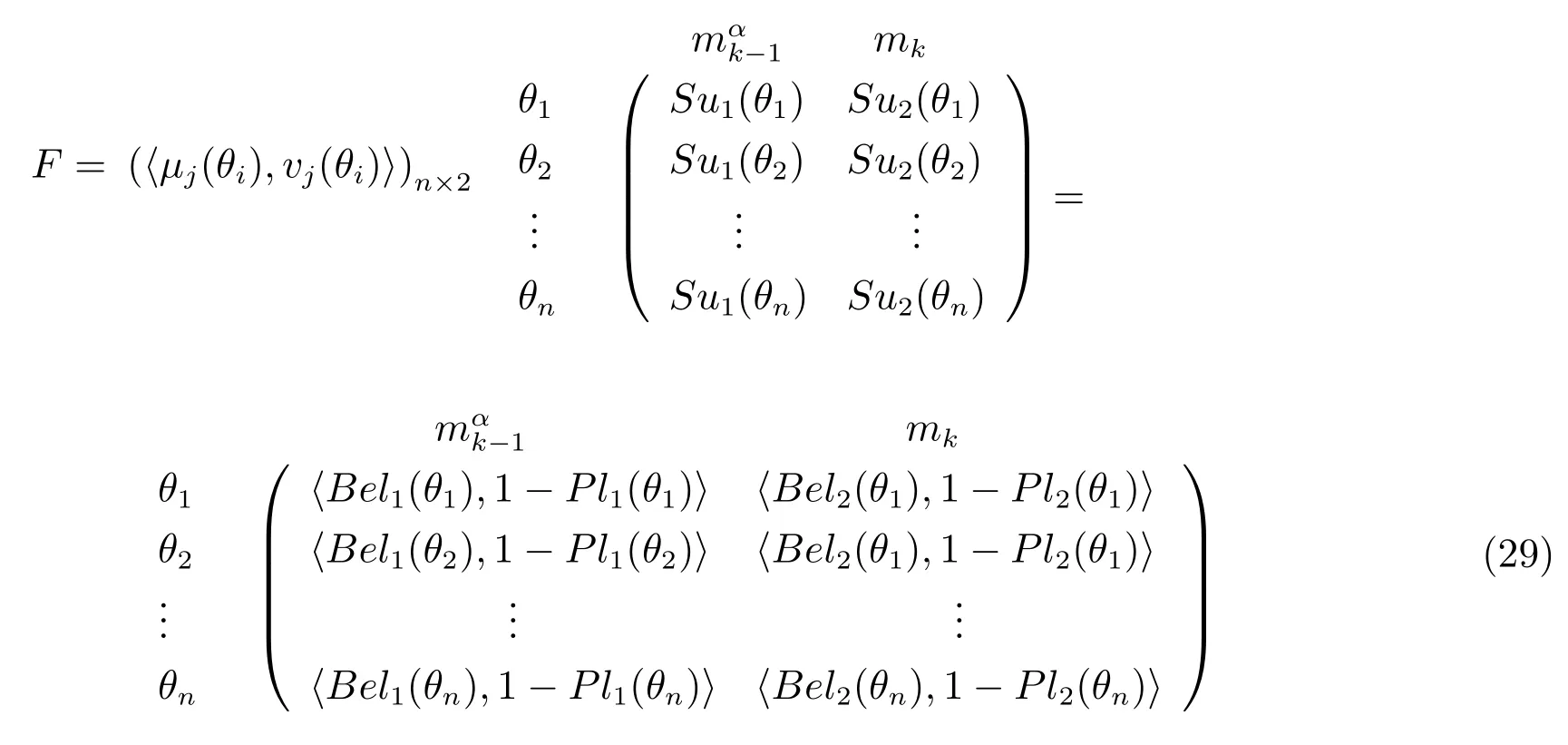
6）θi（i=1，2，···，n）條件下Su1（θi）與Su2（θi）之間的對比關系矩陣為

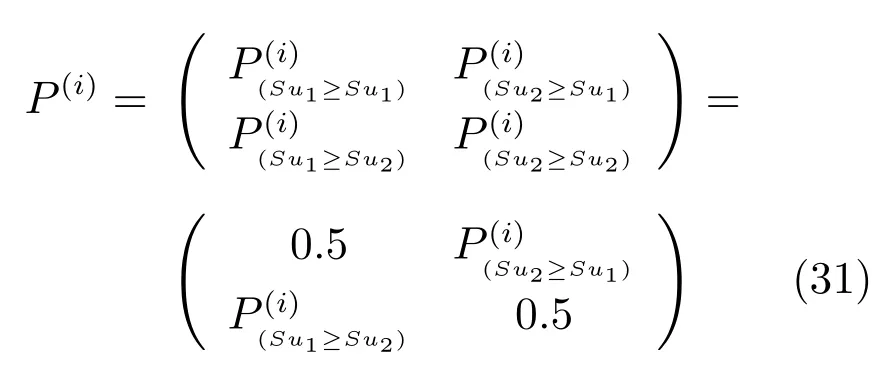
7）根據P（i）的行和，可得到θi賦予和 mk的權重分別為

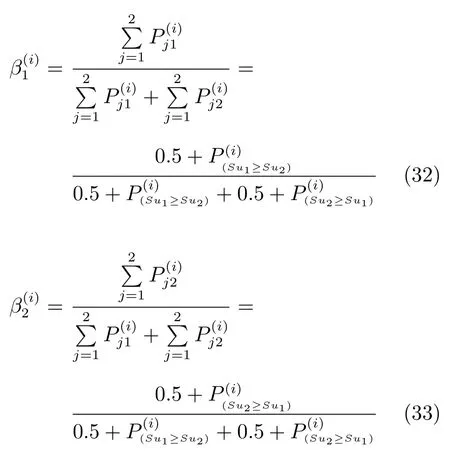
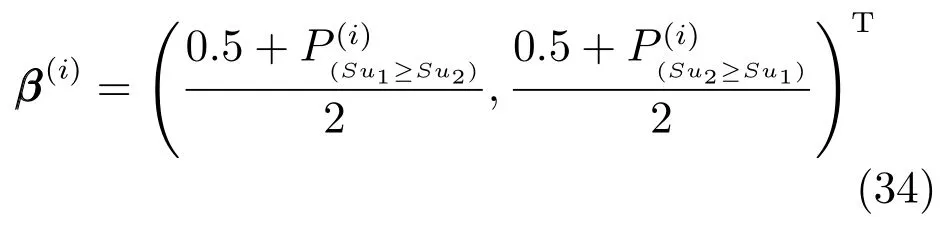
8）構造矩陣W=?β（1），β（2），···，β（n）￠，矩陣WWT的最大特征值對應的特征向量即為和 mk的權重向量β=（β1，β2）T，即β滿足

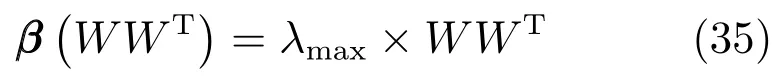
9）為保證β的各分量均為正值，對β進行歸一化可得

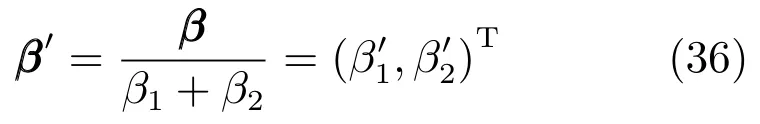
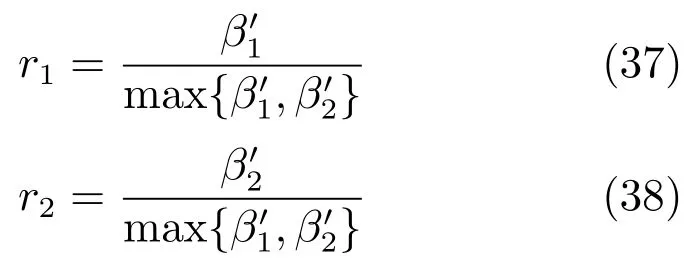
由于r1為證據相對于mk的可靠性因子，r2為mk相對于的可靠性因子，因此，以上證據可靠性評估方法稱為相對可靠性評估（Relative reliability evaluation，RRE），r1和r2稱為相對可靠性因子（Relative reliability factor，RRF）.

4.2時域證據復合可靠度與證據折扣組合方法

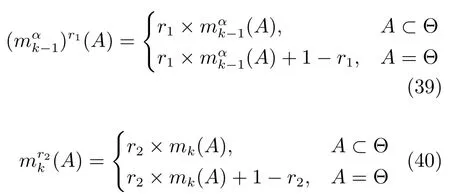
得到mk-1和mk的復合可靠性因子后，可以按照Shafer折扣準則對mk-1和mk進行折扣運算，然后再運用Dempster組合規則進行組合，該過程稱為基于復合可靠度的時域證據組合方法（Temporal evidence combination based on CRF，TEC-CRF），按照此方法進行遞歸融合即可獲得最終融合結果.根據時空信息遞歸分布無反饋融合模型［11］，可以得到基于復合可靠度的時空證據序貫組合方法，如圖1所示.其中，虛線箭頭表示證據折扣運算，點劃線箭頭表示運用Dempster組合規則進行證據組合，運用該方法可以對基于多傳感器的時空信息進行融合.

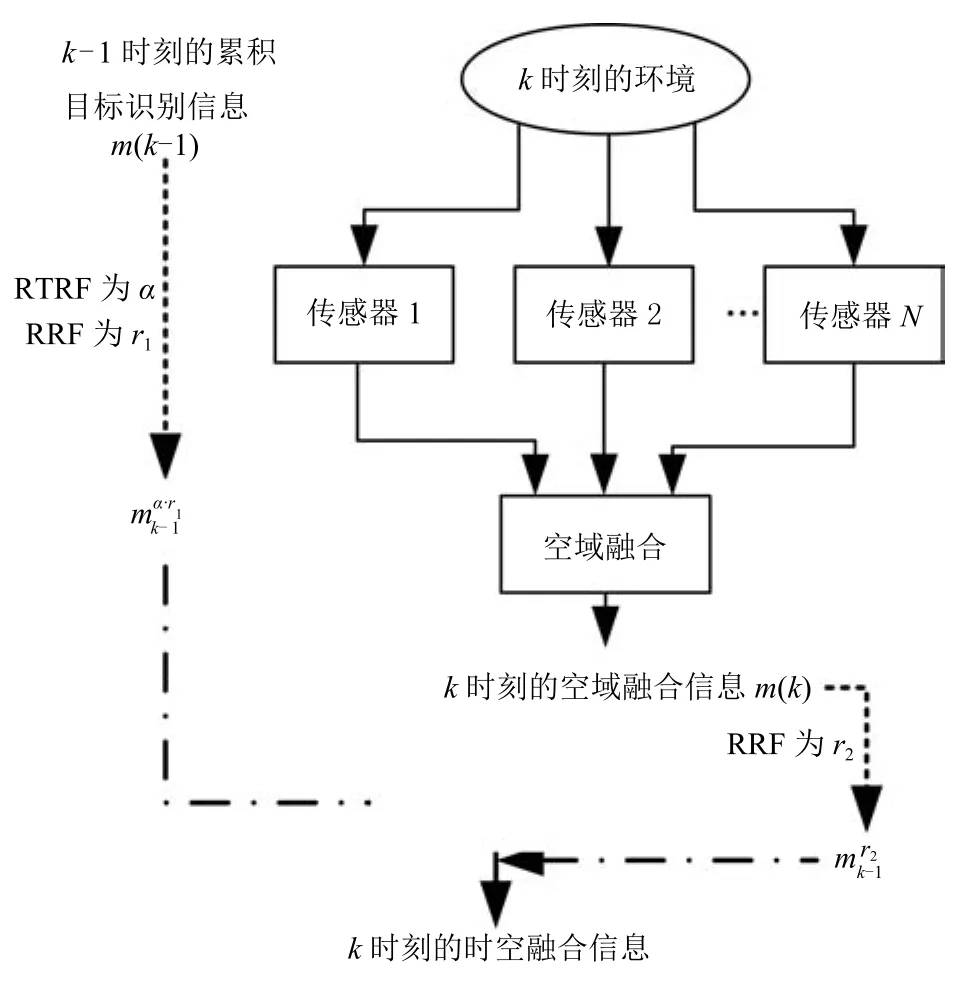
圖1　基于復合可靠度的時空證據序貫組合流程Fig.1The flowchart of spatial-temporal evidence combination based on TEC-CRF

4.3數值算例與仿真

本小節通過決策層融合中的數值算例和實驗仿真對基于復合可靠度的時域證據組合（TEC-CRF）方法的性能進行分析.

4.3.1沖突處理能力分析

例2.設辨識框架為Θ=｛θ1，θ2，θ3｝，融合識別系統在t1=10s時的累積識別結果對應的BPAF為m1，在當前時刻t2=12s獲得的最新識別信息對應的BPAF為m2，m1和m2分別表示如下：

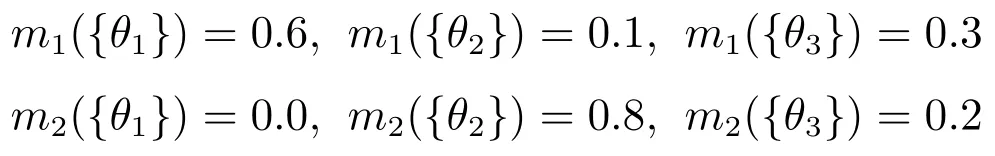
在本算例中計算實時可靠性因子時，取λ=0.1.

m1與m2在t2時刻的實時可靠性因子（RTRF）為

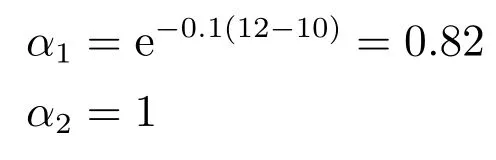
m1按照其在當前時刻的RTRF折扣后的BPAF為

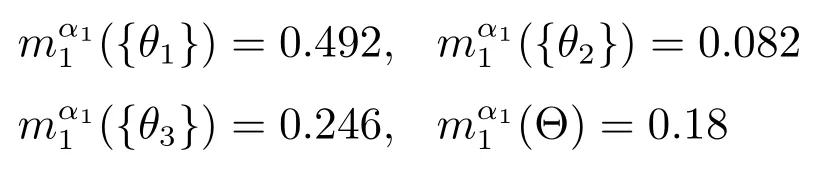
由此可得m1與m2在t2時刻的復合可靠性因子為c1=0.82，c2=0.48.

依據復合可靠性因子分別對m1和m2進行折扣可得

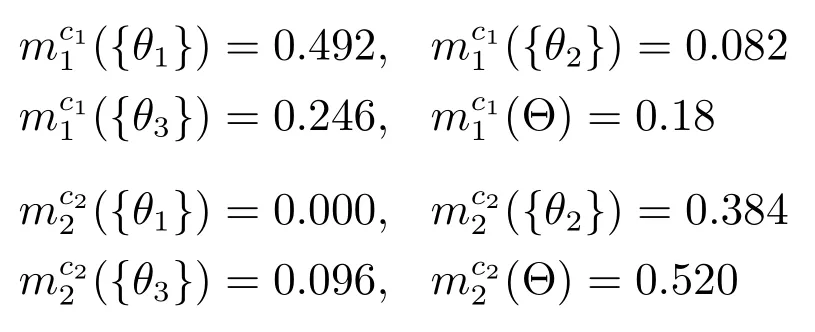
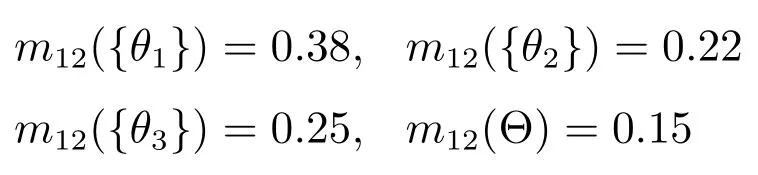
可以看出，最終的融合結果中對｛θ1｝的支持度最大，與m1支持的命題一致.如果直接采用Dempster組合規則，那么將會出現m12（｛θ1｝）=0，即使后面再獲取的證據支持｛θ1｝，聚焦在｛θ1｝上的BPM將一直為0，從而陷入“一票否決”的困境.單純依靠實時可靠性因子得到的結果中，m12（｛θ1｝）= 0，m12（｛θ2｝）=0.71，m12（｛θ3｝）=0.29，雖然隨著后續證據的加入，｛θ1｝的支持度可能會上升，但如果t2時刻就是最后的識別節點，系統在該時刻受到嚴重干擾，那么基于實時可靠性因子的方法將會得到錯誤的結果，導致決策失誤.由此可知，基于復合可靠度的時域證據融合方法能夠較好地處理相鄰證據之間的沖突，有利于做出合理的決策.

4.3.2抗干擾能力分析

例3.在例2的基礎上，系統在t3=15s獲得的識別信息對應的BPAF為m3，為進一步說明該組合方法的性能，分別考慮m3支持θ1和θ2這兩種情況.

1）m3（｛θ1｝）=0.5，m3（｛θ2｝）=0.3，m3（｛θ3｝）=0.2；

2）m3（｛θ1｝）=0.1，m3（｛θ2｝）=0.75，m3（｛θ3｝）=0.15.

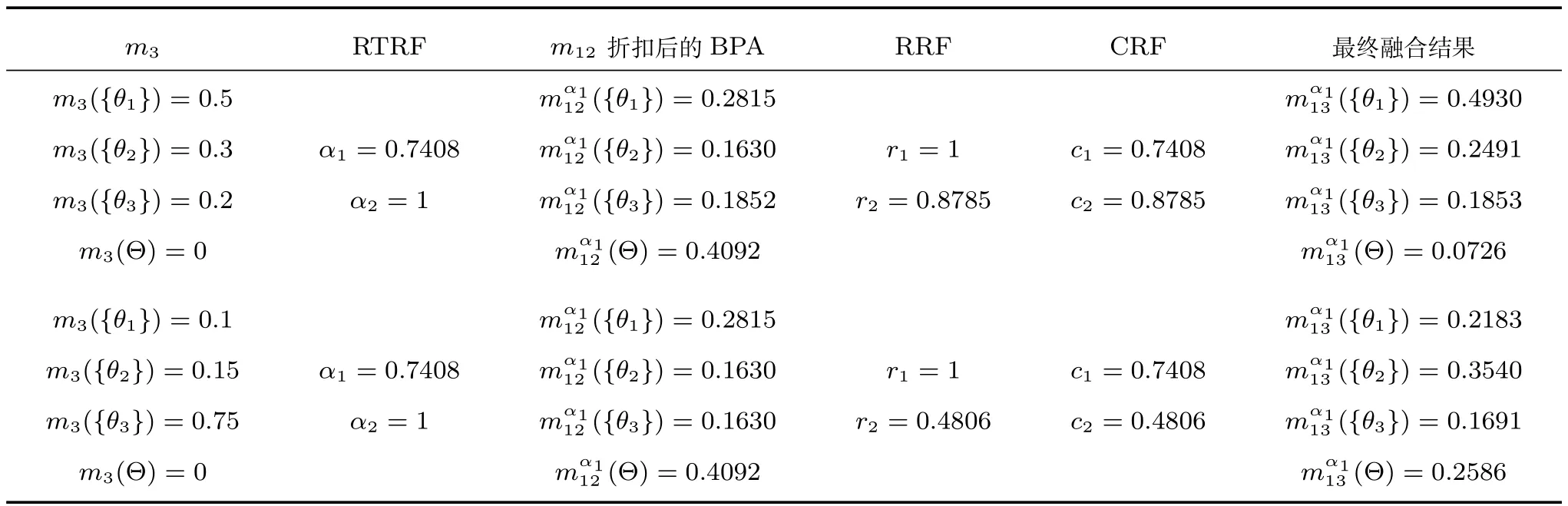
表1　兩種情況下TEC-CRF方法的融合結果Table 1The combination results obtained by TEC-CRF for two cases

按照基于復合可靠度的時域證據組合方法分別對以上兩種情況下的證據進行組合，時域組合結果如表1所示.從表1可以看出，在這兩種情況下獲得的最終結果明顯不同.在情況1）下得到的融合結果支持｛θ1｝，而情況2）下的結果則支持｛θ2｝.情況1）下的m3與m1比較接近，都傾向于支持｛θ1｝，這種情況可以理解為在t2時刻系統受到干擾，獲得錯誤的識別信息，導致在t2時刻的累積識別信息中，｛θ1｝的支持度有所下降；在t3時刻，系統恢復正常，因此此時的融合結果中｛θ1｝的支持度明顯上升，最終決策結果為｛θ1｝.在情況2）下，m3與m2比較接近，都傾向于支持｛θ2｝，可以理解為在t1時刻系統獲得的識別結果有較大偏差，隨著時間的推移，獲取的信息越來越準確，對｛θ2｝的支持度逐漸上升，最終決策結果為｛θ2｝.這表明TEC-CRF方法對證據的變化較為敏感，能夠較好地處理時域融合識別中的沖突信息，有助于提升融合識別系統的抗干擾能力.

為了與Dempster組合方法和文獻［31］中基于實時可靠度的時域證據組合方法進行對比，表2和表3給出了兩種情況下分別運用Dempster方法和基于實時可靠度的時域證據組合方法（Temporal evidence combination based on RTRF，TECRTRF）的融合結果.

表2　兩種情況下Dempster方法的融合結果Table 2The combination results obtained by Dempster＇s rule for two cases

表3　兩種情況下TEC-RTRF方法的融合結果Table 3The combination results obtained by TEC-RTRF for two cases

可以看出，在情況1）下，系統在t2時刻受到干擾，運用Dempster組合方法時，由于沒有考慮證據的可靠性，得到的融合結果對｛θ1｝的支持度為0，盡管后續的證據對｛θ1｝的支持度較大，但最終的融合結果依然不支持｛θ1｝，系統無法從干擾狀態恢復出來；運用TEC-RTRF方法雖然在t3的融合結果中｛θ1｝的支持度有所上升，但增幅較小，系統雖然可以從干擾狀態恢復，但恢復速度較慢.

在情況2）下，可以認為是初始時刻的信息偏差較大，運用Dempster組合方法和TEC-RTRF方法都有利于得到正確的結果，但存在較大風險，如果后續時刻再次受到干擾，那么融合識別系統將無法恢復或恢復速度較慢.對比這三種方法可知，TECCRF方法的抗干擾能力最強，具有較高的可靠性，對初始干擾、識別過程中的干擾都有較強的抵抗能力，適合用來進行時域信息融合.不考慮證據折扣的經典Dempster組合方法和TEC-RTRF方法的抗干擾能力則非常有限，在時域證據融合中的適用性較差.

4.3.3數值仿真

本仿真基于彈道中段目標綜合識別仿真系統開展，本系統立足于在多傳感器平臺，在有限時間內對目標進行連續觀測，多次識別采用圖1所示的時空證據組合流程進行融合識別.

在綜合識別仿真系統中，6個傳感器位于不同的平臺上，各傳感器之間以及同一雷達各時間節點之間的探測信息互不影響，滿足證據理論中各證據源相互獨立的要求，特征提取及分類器設計不屬于本文研究范疇，故在此不作具體說明.待識別目標可能的類別為：彈頭、氣球和碎片，因此，辨識框架為Θ =｛θ1（彈頭），θ2（氣球），θ3（碎片）｝，根據6個傳感器在連續5個時間節點的探測信息對目標類別進行識別，基于某特定戰情設置，各傳感器在各識別節點的識別結果對應的BPAF如表4所示.

表5和表6給出了在5個時間節點對各傳感器的識別結果進行融合得到的空域融合結果.在空域融合中可以選用的方法較多，因此這里只給出了利用經典Dempster組合方法和文獻［32］中提出的基于證據信任度和虛假度的證據組合方法（EC-CF方法）的計算結果.

從表5和表6中可以看出，在t1時刻兩種方法的計算結果有較大差異，這是由于在該時刻的識別結果中，傳感器S5獲得的結果與其他5個傳感器的識別結果直接有較大的沖突，直觀來看，S1，S2，S3，S4，S6這5個傳感器的識別結果都支持｛θ3｝，只有S5傾向于｛θ1｝，因此該時刻的融合結果應該賦予｛θ3｝最大的支持度，可見運用EC-CF方法可以得到與直觀分析一致的融合結果.從t2～t5時刻的空域融合結果可看出，對于低沖突證據而言，EC-CF方法與Dempster方法的結果相差不大；另外，由于該實驗中識別框架的基數不大，而且各BPAF均聚焦在單元素子集上，相對于Dempster方法，EC-CF方法不會帶來時間復雜度的大幅提升，因此在空域融合中，可以運用EC-CF方法對各傳感器的識別結果進行融合，以降低沖突信息的影響.接下來的時域融合即為對在各時間節點使用EC-CF方法獲得的空域融合結果進行序貫融合，該仿真實驗中證據可靠度衰減因子λ的取值為0.05.

為了對比分析TEC-CRF方法在時空信息融合中的性能，表7給出了使用Dempster組合規則進行時域證據累積的結果，表8給出了運用TEC-CRF方法獲得各時間節點的時域累積識別結果.

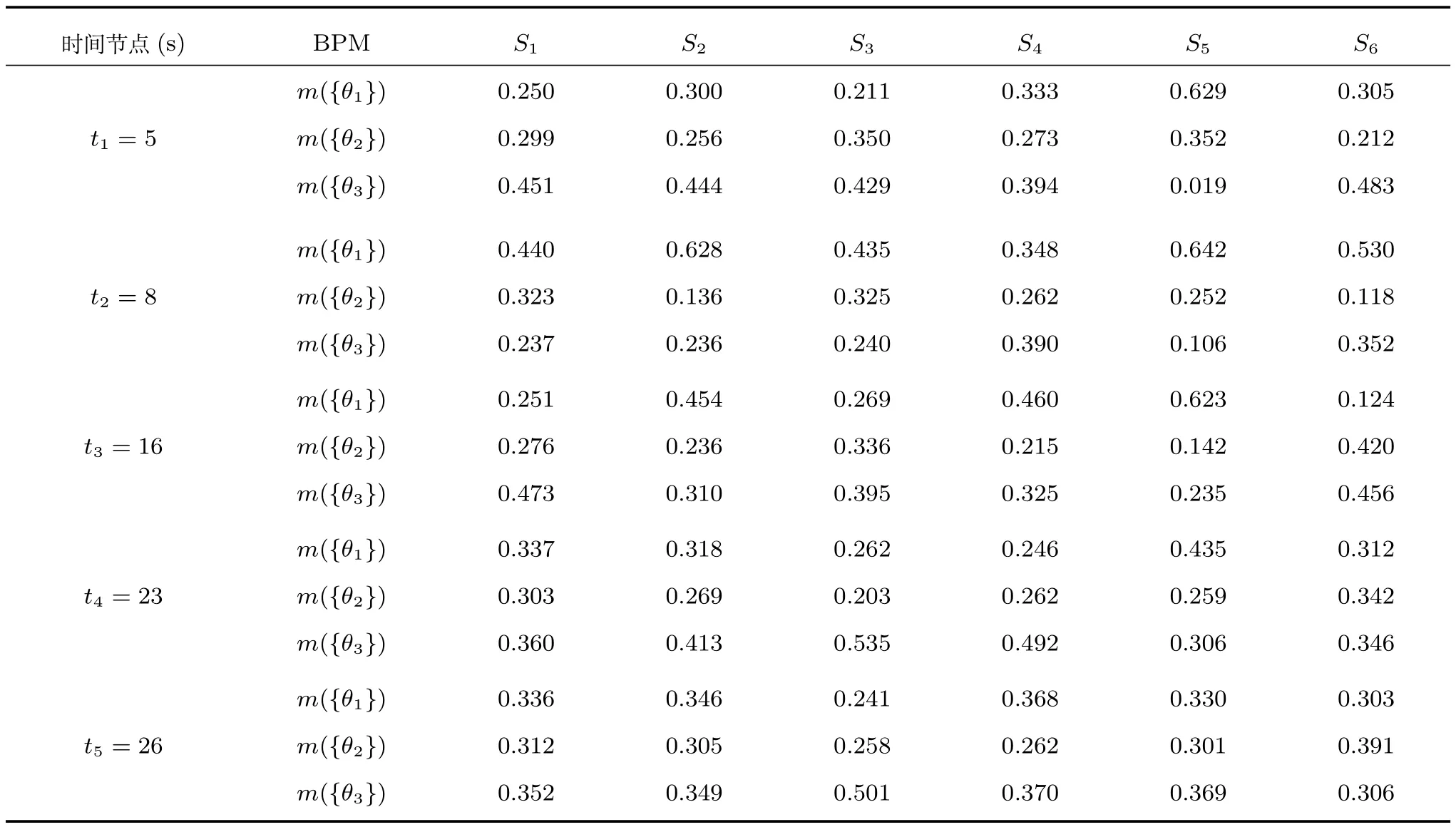
表4　各傳感器在不同時間節點的識別結果Table 4Recognition results of each sensor at all time nodes

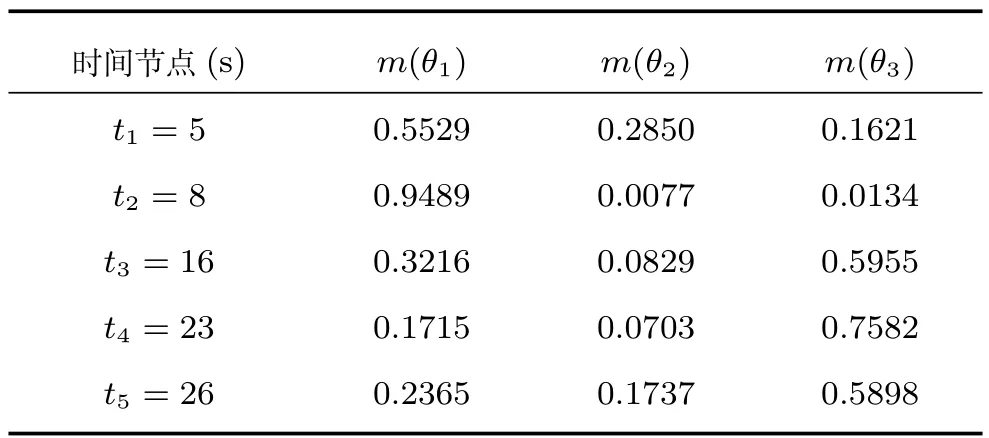
表5　運用Dempster組合規則獲得的空域融合結果Table 5Spatial evidence combination results obtained by Dempster＇s rule

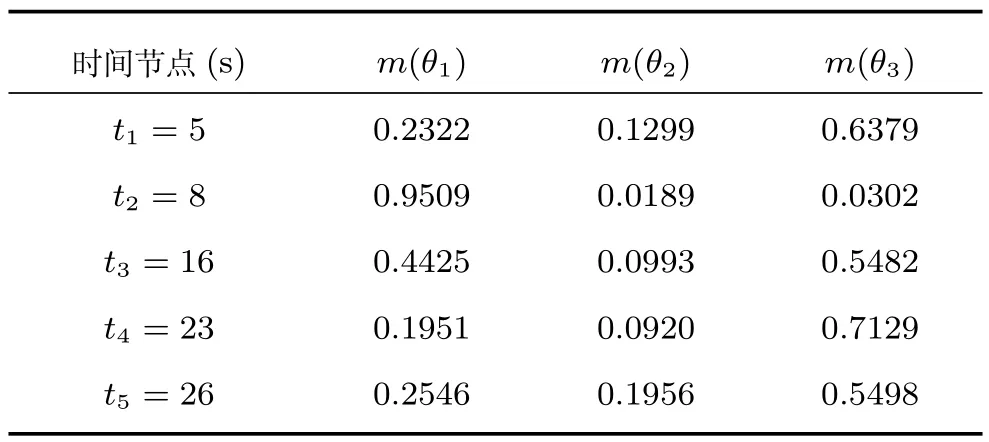
表6　運用EC-CF方法獲得的空域融合結果Table 6Spatial evidence combination results obtained by EC-CF

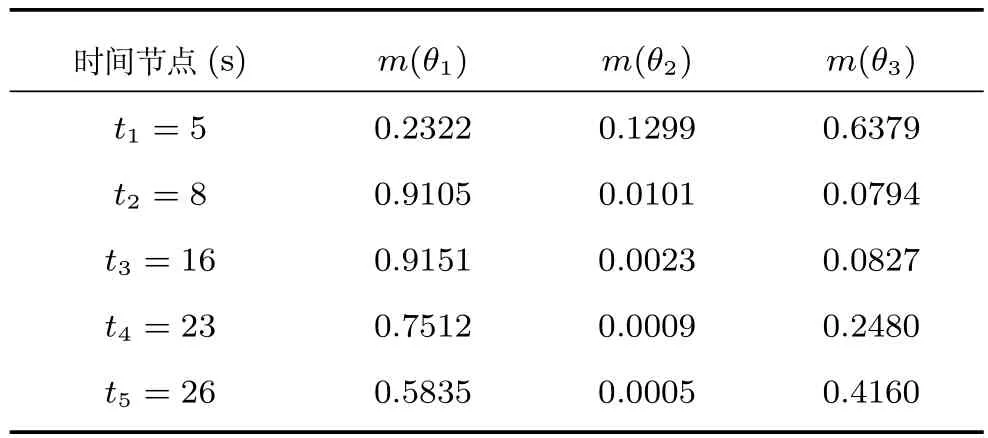
表7　運用Dempster組合規則獲得的時域累積融合結果Table 7Spatial evidence combination results obtained by Dempster＇s rule

從表7和表8中可以看出，在t2=8s的時候，系統受到干擾，導致該時刻的累積識別結果對｛θ1｝的支持度大于｛θ3｝，但隨著后續識別信息的加入，兩種組合方法都可以使｛θ3｝的支持度逐漸上升，但由于TEC-CRF方法考慮了時域證據可靠性的衰減以及相鄰證據間的相對可靠度，因此運用TEC-CRF方法可以使系統盡快地從干擾狀態恢復過來，到t5=26s時，可以得到最終的識別結果為｛θ3｝，而在此時運用Dempster組合方法的結果則依然將目標識別為｛θ1｝，與直觀分析不一致.

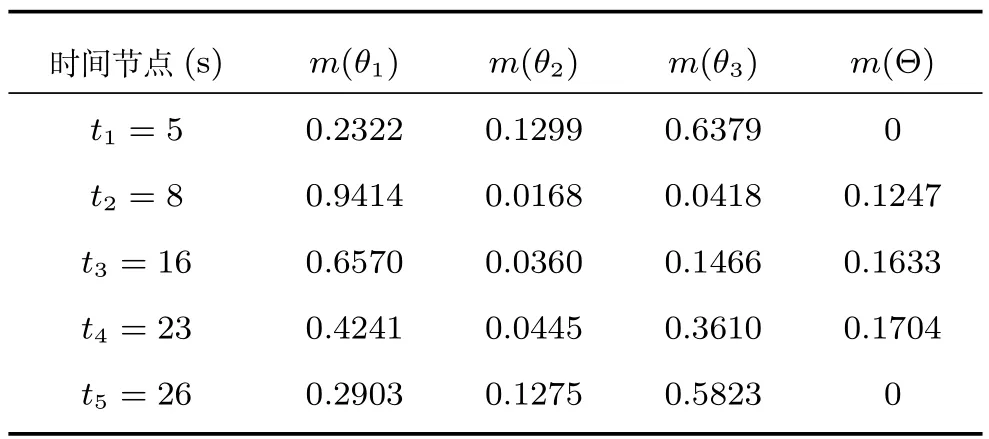
表8　運用TEC-CRF方法獲得的時域累積融合結果Table 8Temporal evidence accumulation results obtained by TEC-CRF

為便于進行直觀分析，圖2和圖3分別給出了基于Dempster方法和TEC-CRF方法進行時域融合時Pignistic概率分布隨時間的變化趨勢.從圖中可以看出，運用Dempster方法進行時域融合時，在t2時刻以后，BetPm｛θ1｝下降的較慢，而BetPm｛θ3｝上升的也較慢，到t5=26s時，BetPm｛θ1｝依然大于BetPm｛θ3｝，因此目標被識別為｛θ1｝.而運用TEC-CRF方法進行時域融合時，在干擾過后，BetPm｛θ1｝急劇下降，BetPm｛θ3｝上升的速度也較快，在最終時刻由BetPm｛θ2｝＜BetPm｛θ1｝＜BetPm｛θ3｝，可將目標識別為｛θ3｝，符合直觀分析.這說明基于TEC-CRF的時域融合方法更有利于進行實時決策.

根據兩種方法的計算過程可知，運用Dempster組合方法進行時域證據組合時，沒有考慮時間因素的影響，只是單純地將證據序列依次組合.本文提出的TEC-CRF方法則充分考慮了時域證據融合的兩個顯著特點，即證據可靠度隨時間的變化和相鄰兩個時間節點獲得的證據之間的相互關系.為了說明時間因素對時域證據融合的影響，對本例中t1時刻獲得的證據mt1與t2時刻獲得的證據mt2進行交換，即各傳感器在t1時刻和t2時刻獲得的識別結果對應的BPAF如表9所示，其余各時間節點的識別結果保持不變.

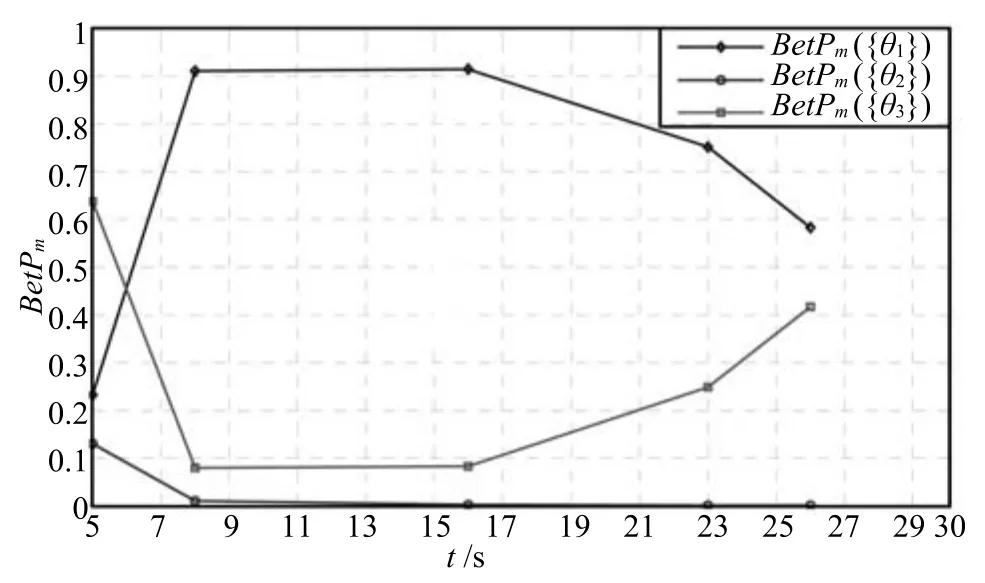
圖2　基于Dempster組合方法的時域累積融合結果Fig.2Temporal evidence accumulation results obtained by Dempster＇s rule

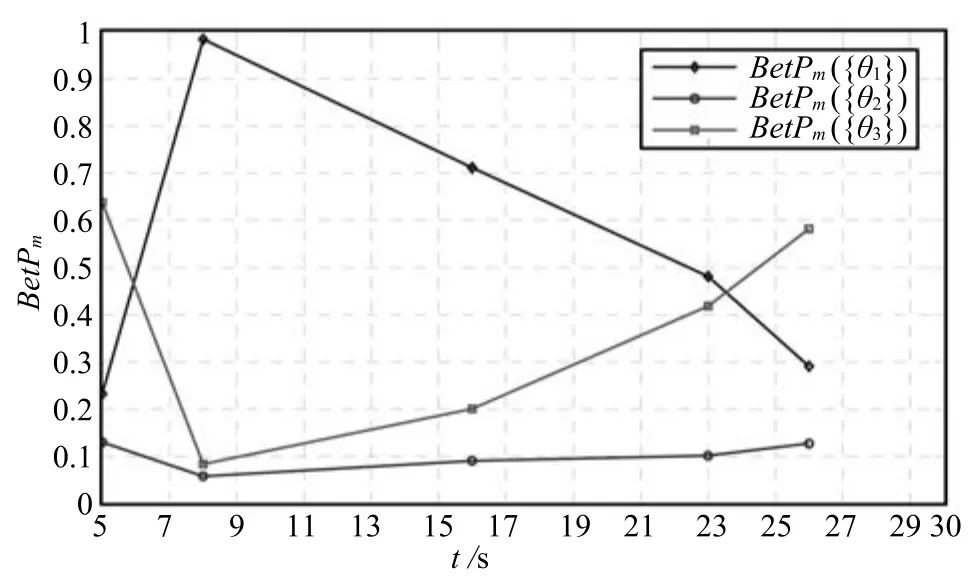
圖3　基于TEC-CRF方法的時域累積融合結果Fig.3Temporal evidence accumulation results obtained by TEC-CRF

表10和表11給出了mt1與mt2交換后各時刻的空域融合結果，可以看出在t1和t2時刻的空域融合結果進行了互換，其余時刻的空域融合結果則保持不變，符合空域證據融合的特點.

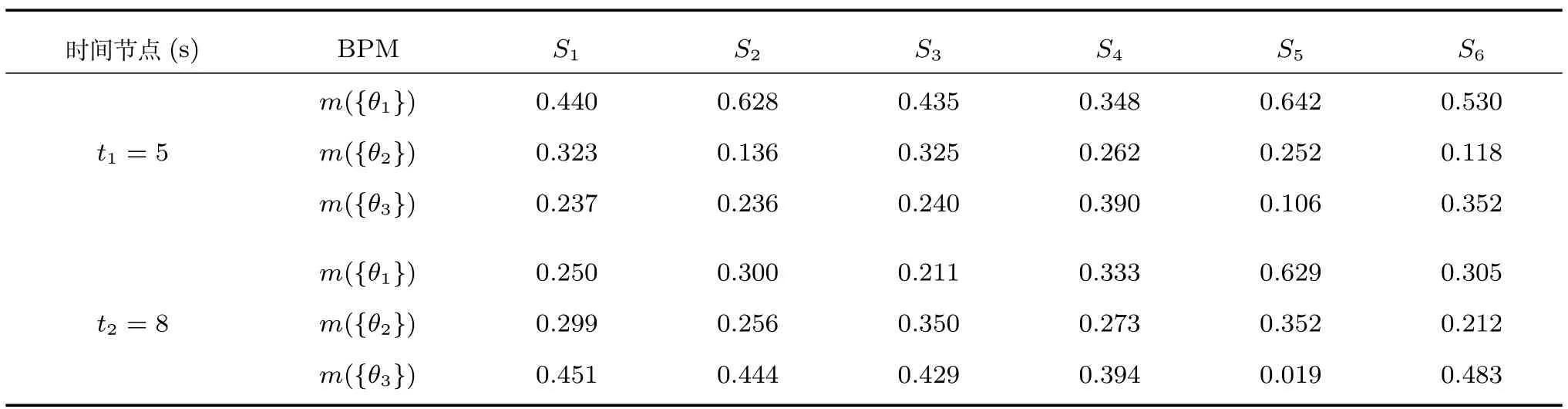
表9　各傳感器在t1和t2時刻的識別結果Table 9Recognition results of each sensor at t1and t2

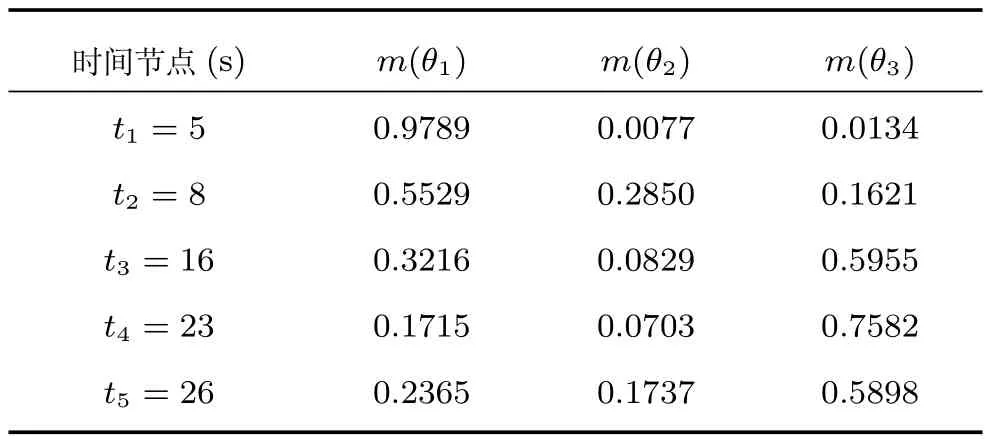
表10　基于Dempster方法的空域融合結果Table 10Spatial evidence combination results based on Dempster＇s rule

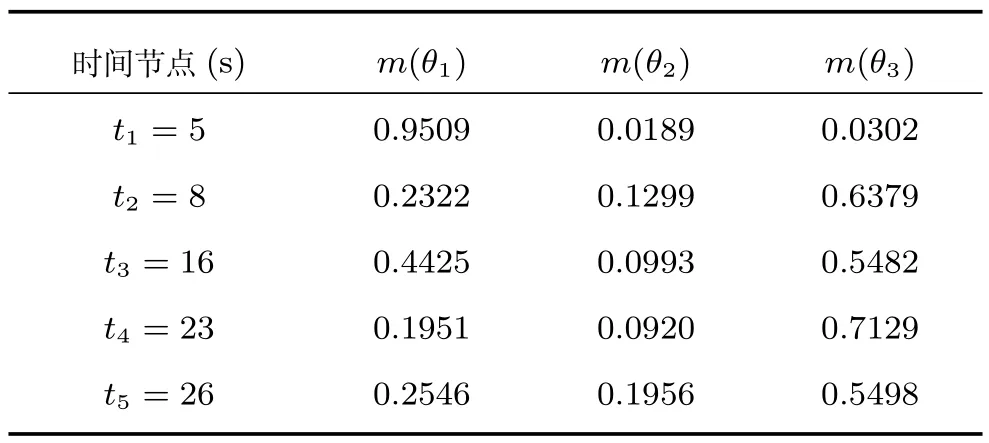
表11　基于EC-CF方法的空域融合結果Table 11Spatial evidence combination results based on EC-CF

運用Dempster組合方法和TEC-CRF方法對表11中運用EC-CF方法獲得的空域融合結果進行時域累積，各時刻的時域累積融合結果如表12和表13所示.

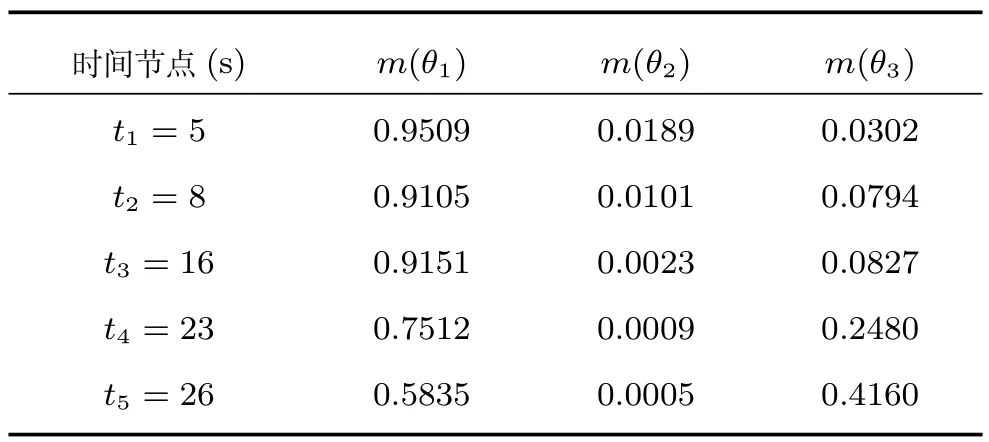
表12　基于Dempster方法的時域累積融合結果Table 12Temporal evidence combination results based on Dempster＇s rule

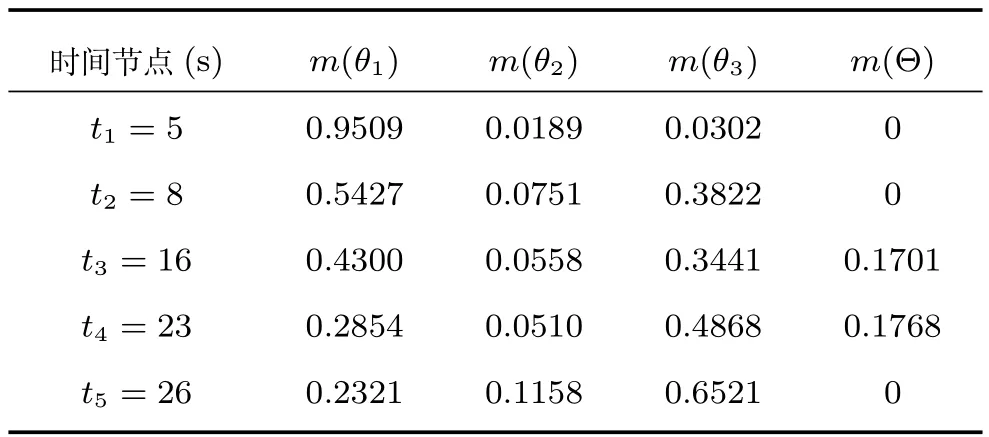
表13　基于TEC-CRF方法的時域累積融合結果Table 13Temporal evidence accumulation results based on TEC-CRF

對比表12和表7可看出，運用Dempster組合規則時，除了t1時刻的累積融合結果即該時刻的空域融合結果發生變化外，其余各時間節點的累積識別結果不會發生變化，表現出了與空域融合相同的特點，沒能體現時域證據融合動態性的特點.

從表13可以看出，TEC-CRF方法在任一時刻獲得的累積融合結果都與表8中對應的結果不同，由于t1時刻的空域融合結果與后續的結果沖突較大，而后續各時刻的空域融合結果之間沖突較小，因此可以認為系統在t1時刻受到干擾或信息不準確而導致識別信息有較大偏差.隨著對目標的不斷識別，t1時刻結果的可靠度逐漸降低，新到的識別信息較為準確而且可靠度較高，因此時域累積識別結果不斷更新.可以看出在新的條件下，根據t4時刻的累積結果即可做出合理的決策，t5時刻的累積結果則進一步增強了決策的合理性，充分體現了時域證據融合結果的繼承與更新.而且，容易驗證，使用TEC-CRF方法時，任何兩個時間間隔的改變、識別信息獲取順序的改變都可能會帶來時域融合結果的變化，這說明TEC-CRF方法對時間是敏感的，符合時域信息融合的特點.

同樣，為直觀分析mt1與mt2的交換帶來時域累積融合結果的變化，圖4和圖5分別給出了mt1與mt2交換后，兩種方法獲得的Pignistic概率變化趨勢.對比圖4與圖2可以看出，運用Dempster組合方法進行時域融合時，除了在初始時刻的Pignistic概率分布不相同以外，前兩個時間節點信息的交換并不影響后續各時刻的Pignistic概率分布.對圖5和圖3進行對比可知，運用TEC-CRF方法時，mt1與mt2的交換造成所有時刻的累積融合結果都發生了變化，表明TEC-CRF方法可以充分體現時間因素對時域融合的影響.

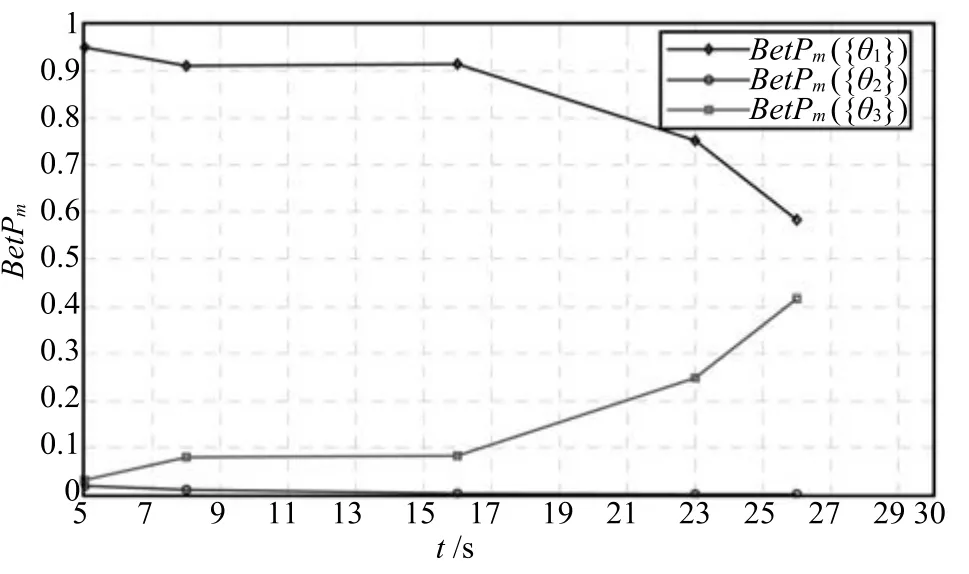
圖4　Dempster方法獲得的Pignistic概率Fig.4The Pignistic probability obtained by Dempster＇s rule

5　結束語

為了實現基于證據理論的時域不確定信息融合，進一步增強時空信息融合系統對沖突信息的處理能力，本文在對時域證據融合中相鄰時間節點間的信息進行對比分析的基礎上，結合基于直覺模糊多屬性決策的證據可靠性評估方法，給出了相對可靠度的概念，在此基礎上結合時域證據可靠度衰減模型及時域證據實時可靠度的概念，提出了一種基于復合可靠度的時域證據組合方法（TEC-CRF）方法，基于TEC-CRF方法構建了時空信息序貫融合模型.數值算例和實驗仿真驗證了TEC-CRF方法的性能特點，結果表明，TEC-CRF方法可以較好地處理時域信息間的沖突，對時間變化較為敏感，充分體現了時域融合動態性的特點，即當前時刻融合結果是對前一時刻融合結果的繼承與更新.需要說明的是，時域信息融合是一個復雜的工程問題，在實際應用中還有諸多因素需要考慮，為實現時域信息的有效融合，有必要將本文所提方法與其他相關理論結合起來，這也是我們下一步的研究方向.

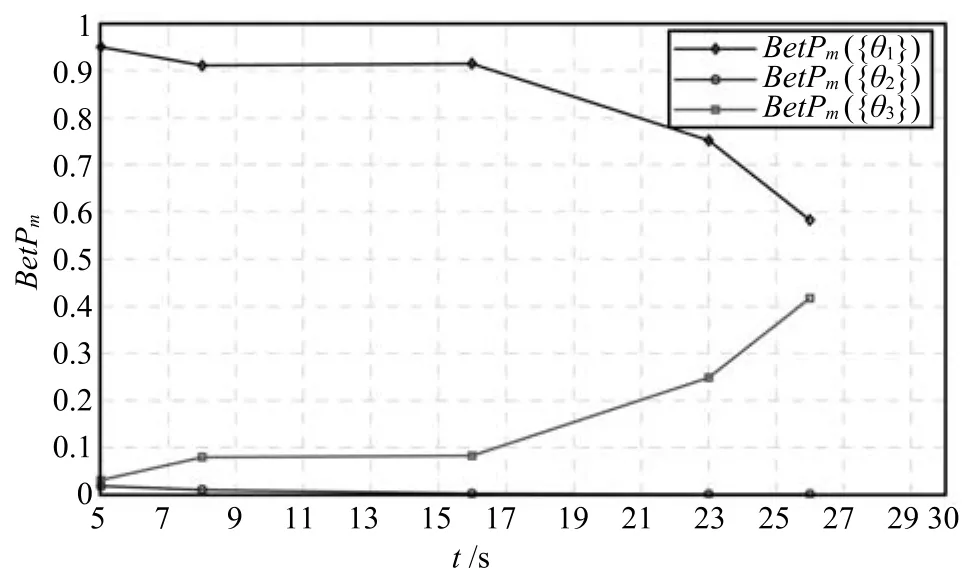
圖5　TEC-CRF方法獲得的Pignistic概率Fig.5The Pignistic probability obtained by TEC-CRF

References

1 Dempster A P.Upper and lower probabilities induced by a multivalued mapping.The Annals of Mathematical Statistics，1967，38（2）：325-339

2 Shafer G.A Mathematical Theory of Evidence.Princeton，NJ：Princeton University Press，1976.

3 Pan Quan，Yu Xin，Cheng Yong-Mei，Zhang Hong-Cai.Essential methods and progress of information fusion theory. Acta Automatica Sinica，2003，29（4）：599-615（潘泉，于昕，程詠梅，張洪才.信息融合理論的基本方法與進展.自動化學報，2003，29（4）：599-615）

4 Zadeh L A.A simple view of the Dempster-Shafer theory of evidence and its implication for the rule of combination. The AI Magazine，1986，7（2）：85-90

5 Yang Yi，Han De-Qiang，Han Chong-Zhao.Evidence combination based on multi-criteria rank-level fusion.Acta Automatica Sinica，2012，38（5）：823-831（楊藝，韓德強，韓崇昭.基于多準則排序融合的證據組合方法.自動化學報，2012，38（5）：823-831）

6 Zhou Zhe，Xu Xiao-Bin，Wen Cheng-Lin，Lv Feng.An optimal method for combining conflicting evidences.Acta Automatica Sinica，2012，38（6）：976-985（周哲，徐曉濱，文成林，呂鋒.沖突證據融合的優化方法.自動化學報，2012，38（6）：976-985）

7 Deng Yong，Shi Wen-Kang.A modified combination rule of evidence theory.Journal of Shanghai Jiaotong University，2003，37（8）：1275-1278（鄧勇，施文康.一種改進的證據推理組合規則.上海交通大學學報，2003，37（8）：1275-1278）

8 Murphy C K.Combining belief functions when evidence conflicts.Decision Support Systems，2000，29（1）：1-9

9 Deng Y，Shi W K，Zhu Z F，Liu Q.Combining belief functions based on distance of evidence.Decision Support Systems，2004，38（3）：489-493

10 Han De-Qiang，Han Chong-Zhao，Deng Yong，Yang Yi. Weighted combination of conflicting evidence based on evidence variance.Acta Electronica Sinica，2011，39（3A）：153-157（韓德強，韓崇昭，鄧勇，楊藝.基于證據方差的加權證據組合.電子學報，2011，39（3A）：153-157）

11 Hong L，Lynch A.Recursive temporal-spatial information fusion with applications to target identification.IEEE Transactions on Aerospace and Electronic Systems，1993，29（2）：435-445

12 Hong Zhao-Yi，Gao Xun-Zhang，Li Xiang.Research on temporal-spatial information fusion model based on DS theory.Signal Processing，2011，27（1）：14-19（洪昭藝，高勛章，黎湘.基于DS理論的混合式時空域信息融合模型.信號處理，2011，27（1）：14-19）

13 Liu Yong-Xiang，Zhu Yu-Peng，Li Xiang，Zhuang Zhao-Wen.Integrated target discrimination model in missile defense system.Journal of Electronics and Information Technology，2006，28（4）：638-642（劉永祥，朱玉鵬，黎湘，莊釗文.導彈防御系統中的目標綜合識別模型.電子與信息學報，2006，28（4）：638-642）

14 Wu Jun，Cheng Yong-Mei，Qu Sheng-Jie，Pan Quan，Liu Zhun-Ga.An effective multi-platform multi-radar target identification algorithm based on three level fusion hierarchical structure.Journal of Northwestern Polytechnical University，2012，30（3）：367-372（吳俊，程詠梅，曲圣杰，潘泉，劉準釓.基于三級信息融合結構的多平臺多雷達目標識別算法.西北工業大學學報，2012，30（3）：367-372）

15 Daniel M.Probabilistic transformations of belief functions. Symbolic and Quantitative Approaches to Reasoning with Uncertainty.Berlin Heidelberg：Springer，2005.539-551

16 Smets P，Kennes R.The transferable belief model.Artificial Intelligence，1994，66（2）：191-234

17 Zadeh L A.Fuzzy sets.Information and Control，1965，8（3）：338-353

18 Atanassov K T.Intuitionistic furzy sets.Fuzzy Sets and Systems，1986，20（1）：87-96

19 Bustince H，Burillo P.Vague sets are intuitionistic fuzzy sets.Fuzzy Sets and Systems，1996，79（3）：403-405

20 Hong D H，Kim C.A note on similarity measures between vague sets and between elements.Information Sciences，1999，115（1-4）：83-96

21 Li J P，Yang Q B，Yang B.Dempster-Shafer theory is a special case of Vague sets theory.In：Proceedings of the 2004 International Conference on Information Acquisition.Hefei，China：IEEE，2004.50-53

22 Dymova L，Sevastjanov P.An interpretation of intuitionistic fuzzy sets in terms of evidence theory：decision making aspect.Knowledge-Based Systems，2010，23（8）：772-782

23 Dymova L，Sevastjanov P.The operations on intuitionistic fuzzy values in the framework of Dempster-Shafer theory. Knowledge-Based Systems，2012，35：132-143

24 Yager R R.An intuitionistic view of the Dempster-Shafer belief structure.Soft Computing，2014，18（11）：2091-2099

25 Xing Qing-Hua，Liu Fu-Xian.Method of determining membership and nonmembership function in intuitionistic fuzzy sets.Control and Decision，2009，24（3）：393-397（邢清華，劉付顯.直覺模糊集隸屬度與非隸屬度函數的確定方法.控制與決策，2009，24（3）：393-397）

26 Guo H，Shi W，Deng Y.Evaluating sensor reliability in classification problems based on evidence theory.IEEE Transactions on Systems，Man，and Cybernetics—Part B：Cybernetics，2006，36（5）：970-981

27 Elouedi Z，Mellouli K，Smets P.Assessing sensor reliability for multisensor data fusion within the transferable belief model.IEEE Transactions on Systems，Man，and Cybernetics—Part B：Cybernetics，2004，34（1）：782-787

28 Yang Wei，Jia Yu-Ping，Fu Yao-Wen.Research on fusion recognition algorithm for different reliable sensors based on the belief function theory.Signal Processing，2009，25（11）：1766-1770（楊威，賈宇平，付耀文.傳感器可靠性相異的信任函數理論融合識別算法研究.信號處理，2009，25（11）：1766-1770）

29 Fu Yao-Wen，Jia Yu-Ping，Yang Wei，Zhuang Zhao-Wen. Sensor dynamic reliability evaluation and evidence discount. Systems Engineering and Electronics，2012，34（1）：212-216（付耀文，賈宇平，楊威，莊釗文.傳感器動態可靠性評估與證據折扣.系統工程與電子技術，2012，34（1）：212-216）

30 Nakahara Y.User oriented ranking criteria and its application to fuzzy mathematical programming problems.Fuzzy Sets and Systems，1998，94（3）：275-286

31 Song Y F，Wang X D，Lei L，Xing Y Q.Credibility decay model in temporal evidence combination.Information Processing Letters，2015，115（2）：248-252

32 Song Ya-Fei，Wang Xiao-Dan，Lei Lei，Xue Ai-Jun.Evidence combination based on the degree of credibility and falsity.Journal on Communications，2015，36（5）：2015104-1-2015104-6（宋亞飛，王曉丹，雷蕾，薛愛軍.基于信任度和虛假度的證據組合方法.通信學報，2015，36（5）：2015104-1-2015104-6）

宋亞飛空軍工程大學防空反導學院講師.2015年在空軍工程大學獲博士學位.主要研究方向為模式識別，智能信息處理，證據推理.本文通信作者.

E-mail：yafei_song@163.com

（SONG Ya-FeiLecturer at the College of Air and Missile Defense，Air Force Engineering University（AFEU）. He received his Ph.D.degree from AFEU in 2015.His research interest covers pattern recognition，intelligent information processing，and evidential reasoning.Corresponding author of this paper.）

王曉丹空軍工程大學防空反導學院教授.主要研究方向為模式識別，智能信息處理.

E-mail：afeu_wang@163.com

（WANGXiao-DanProfessor at the College of Air and Missile Defense，Air Force Engineering University（AFEU）.Her research interest covers pattern recognition and intelligent information processing.）

雷蕾空軍工程大學防空反導學院博士研究生.2012年在空軍工程大學獲碩士學位.主要研究方向為模式識別，智能信息處理.

E-mail：wendyandpaopao@163.com

（LEI LeiPh.D.candidate at the College of Air and Missile Defense，Air Force Engineering University（AFEU）. She received her master degree from AFEU in 2012.Her research interest covers pattern recognition and intelligent information processing.）

Combination of Temporal Evidence Sources Based on Intuitionistic Fuzzy Sets

SONG Ya-Fei1WANG Xiao-Dan1LEI Lei1

Evidence theory has been widely used in spatial and temporal information fusion.The sequential and dynamic characteristics of temporal fusion calls for a new combination rule of temporal evidence sources.In this paper，temporal evidence combination is analyzed in the framework of evidence reliability and evidence discounting.A method of temporal evidence combination is proposed based on the composite reliability factor of temporal evidence.A ranking method for intuitionistic fuzzy values is firstly presented，followed by the presentation of evidence reliability evaluation based on intuitionistic fuzzy multiple criteria decision making.Then the relative reliability factors of evidence sources in neighboring time nodes are evaluated.By combining the relative reliability factor and real-time reliability factor yielded by the credibility decay model，a composite reliability factor is obtained.Finally，according to evidence discounting and Dempster＇s combination rule，a method of temporal evidence combination based on the composite reliability factor is proposed.Numerical examples and simulation demonstrate that the proposed method is time sensitive，which can reflect the dynamic nature of temporal information fusion.Moreover，it is illustrated that this method can deal with conflict in temporal fusion well.The proposed temporal evidence combination rule can enhance the anti-interference performance of the target identification fusion system.

Evidence theory，intuitionistic fuzzy sets，temporal evidence combination，reliability evaluation，composite reliability factor，evidence discounting

Manuscript December 10，2015；accepted February 18，2016

10.16383/j.aas.2016.c150829

Song Ya-Fei，Wang Xiao-Dan，Lei Lei.Combination of temporal evidence sources based on intuitionistic fuzzy sets.Acta Automatica Sinica，2016，42（9）：1322-1338

2015-12-10錄用日期2016-02-18

國家自然科學基金（61273275，60975026，61503407，61573375）資助

Supported by National Natural Science Foundation of China（61273275，60975026，61503407，61573375）

本文責任編委陳積明

Recommended by Associate Editor CHEN Ji-Ming

1.空軍工程大學防空反導學院西安710051

1.Air and Missile Defense College，Air Force Engineering University，Xi＇an 710051