灰色理論在BP神經網絡預測中的應用

劉明明

【摘要】 針對灰色系統的不確定性，將灰色理論應用到BP神經網絡預測模型中。首先深入研究了灰色系統理論以及BP神經網絡的原理，并將二者結合建立灰色神經網絡的預測模型。最后，總結了該模型的特性，并對其進行展望。

【關鍵字】 灰色理論 BP神經網絡 預測模型

一、引言

隨著大數據時代的到來，BP神經網絡預測模型已成為學術界研究的熱點，并應用到多領域中。BP神經網絡具有很好的非線性逼近以及自學習的能力，可高精度擬合預測值，但是，由于很多系統存在不確定性，傳統的BP神經網絡將原始時間序列直接作為輸入值，而原始時間序列中具有很大的隨機性和不確定性，使得神經網絡在預測結果中，存在較大偏差。解決此問題的有效方法是將原始時間序列經過灰色理論進行白化處理，過濾掉數列中的不確定性和隨機性等灰色特性，再將白化處理后的結果作為BP神經網絡的輸入。

二、灰色預測理論研究

根據研究對象的特性可將其分為白、灰、黑三類，該分類取決于研究者對系統信息的掌握程度，是基于認識程度而言，具有相對性。其中白色系統信息完全明確，黑色系統信息完全缺乏，而灰色系統是介于白色系統和黑色系統之間，其信息具有不充分、不完全的特性。灰色預測為灰色系統最典型的應用，在樣本數據量較少、預測結果具有一定的隨機性時，灰色理論是應用最為廣泛的，克服了系統周期短和數據不足的矛盾。對于樣本少、貧信息的不確定性系統[1]而言，由于原始數據毫無規律可循，因此灰色理論首先將原始時間序列進行累加，使其具有遞增規律，然后對其進行擬合，最終將累加數據進行還原。其具體原理如下所示：設原始時間序列為累加為時間序列為，累加后是單調不減時間序列，可見，一般累加可將非負的任意無規律數列轉換為單調不減數列。根據該時間序列，建立白化方程并得到方程的解。所得即為的估計值，但是由原始數列累加變換所得，因此，還需對估計值進行累減處理，最終即為所求預測值。

三、BP神經網絡理論研究

BP神經網絡是一種具有連續傳遞函數的前饋神經網絡，其訓練方法是誤差反向傳播算法，常用的為梯度下降法[2]。以均方誤差最小化為目標不斷修改網絡權值和閾值，最終能高精度地擬合數據。BP神經網絡模型結構分為三層，第一層為輸入層，輸入值為預測系統的主要影響因素的定量值；第二層為隱含層，每個神經網絡模型至少包含一個隱含層，為了計算方便，本論文中采用一個隱含層進行預測；第三層為輸出層，輸出即為系統的預測結果，輸出可為一個或多個，本文采用一個輸出模式。設輸入層的輸入值為，隱含層的神經元值為，輸出層的神經元值為。輸入層神經元與隱含層神經元的權值為，隱含層神經元與輸出層神經元的權值為。隱含層神經元的閾值為，激發函數為，輸出層神經元的閾值為，激發函數為。在神經網絡進行訓練時，分為兩個方向：信息正向傳遞和誤差反向傳播。在信息正向傳遞的過程中，隱含層每個神經元通過該神經元的閾值、其與輸入層各神經元的權值及輸入層各神經元本身的值的結合，在本層激勵函數的作用下取得。神經網絡經過以上的正向信息傳遞，將M維向量的N個樣本數據作為輸入，計算出隱含層神經元的值，最后計算出實際輸出值。利用其與期望輸出值T可計算出均方誤差。將所得MSE沿原來正向信息傳遞的路徑逐層反向傳遞，依據輸出的MSE計算出各層的，并將作為依據，更新各連接的閾值和權值，此時誤差反向傳遞完畢。網絡模型反復進行信息正向傳遞和誤差反向傳遞著兩個過程，直到MSE達到標準或小于標準ε。

四、灰色神經網絡預測模型的建立

由于灰色系統具有明顯的不確定性，因此用灰色模型先將原始輸入數據進行累加，使其具有明顯的指數特性，并對其進行白化即用微分方程對其進行擬合預測。對于有N個參數的灰色神經網絡的微分方程為：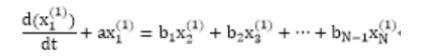

其中，xi（1）（i=2，3，...，N）為系統輸入值，xi（1）為系統輸出值。記微分方程系數為

將GM（1，N）的輸出值作為神經網絡的輸入值，即可得到灰色神經網絡模型。

總結和展望：由于現實世界中的系統很多屬于灰色系統，在對未來數據的預測過程中，僅憑傳統的BP神經網絡預測存在很大的偏差。而本文提出的灰色神經網絡預測模型可以有效地過濾系統中的灰色特性，并充分發揮灰色理論和BP神經網絡各自的優勢，二者取長補短，使得最終對灰色系統的預測更加準確。但值得注意的是在神經網絡預測的過程中，采用的梯度下降法只能找到局部最有值[3]，無法準確獲取全局最優。可在以后的預測模型研究中考慮加入遺傳算法等對此模型進行優化。

參 考 文 獻

[1] 劉金英. 灰色預測理論與評價方法在水環境中的應用研究[D].吉林大學，2004.

[2] 汪鐳. 人工神經網絡理論在控制領域中的應用綜述[J]. 同濟大學學報，2001-29-3：357-361.

[3] 樊振宇. BP神經網絡模型與學習算法[J]. 軟件導刊， 2011-10-7：66-68.