基于多重自由設站在基坑沉降監測中的研究

羅伯成　吳海科

(貴州大學土木工程學院，貴州 貴陽　550025)

?

基于多重自由設站在基坑沉降監測中的研究

羅伯成吳海科

(貴州大學土木工程學院，貴州 貴陽550025)

介紹了全站儀三角高程測量的原理，并以茅臺4號大橋古藺岸工程為例，對全站儀測量位移和沉降精度進行了分析，通過分析結果，選擇了相應的測量儀器，達到了實時、快速和準確反映基坑沉降的目的。

復雜基坑，多重自由設站，沉降監測，監測點

0　引言

在多山地區的基坑監測中，基坑周圍工作面較為狹窄、基坑開挖形狀不規則，采用常規的監測方法往往無法對基坑沉降進行實時監測。為此，我們可以采用在基坑附近自由設站的方法進行監測[1,2]。但以往測量的科研工作者在布置自由設站點時都只有一個或幾個相互獨立的自由設站點，由于開挖基坑和施工場地的特殊性，以上自由設站的方法無法覆蓋整個監測網。為了對整個基坑進行實時監測，在此提出基于多重自由設站的方法對基坑進行沉降監測，也就是為了建立能夠對基坑所有監測點進行監測，采用多個連續自由設站的方法對基坑進行監測。下面就貴州省茅臺4號大橋古藺岸為例來闡述深基坑監測測站點的布置方法的優化。

茅臺4號大橋位于貴州省遵義市茅臺鎮茅臺酒廠附近，交通方便，橋位橫跨赤水河。由于該橋為人行懸索，為保護當地的自然環境，不允許為了施工和監測的需要而大量破壞基坑周圍的自然環境，這就導致監測場地往往較為狹窄。隨著智能型全站儀的應用和普及，采用全站儀隨架隨測的多重自由設站法能有效解決以上監測的困難。

1　全站儀自由設站

1.1全站儀計算坐標的原理

全站儀可以測量測站點與監測點之間的斜距S以及直接測量出監測點相對于測站點的垂直角β，進而全站儀自帶的程序將自動計算出待測點的坐標[3]，其高差計算公式為：ΔH=Ssinβ，其計算理論原理如下：

z監測點=z測站點+i+Ssinβ-v

(1)

其中，z監測點，z測站點分別為監測點和測站點的高程坐標；i為儀器高；v為棱鏡高。

1.2全站儀多重自由設站觀測原理

全站儀自由設站法觀測，它是一種以角度與距離同時測量的極坐標法為基礎，應用自動化高精度全站儀在基坑附近一方便觀測的位置設一觀測站，隨意設置測站點的坐標及任一個方向的方位角進行定向，將其中一個基準點作為后視點，利用全站儀的自動監測功能采用極坐標的方法對每個監測點進行觀測，這樣實際上就是建立了一個自由坐標系，每次都利用其中一個基準點作為測站點，另一個基準點作為后視點，對自由設站的測站點進行監測，進而得到其坐標，然后從觀測站上觀測若干個已知基準點及變形監測點的方向和距離。當聯測這幾個基準點時，基準點就有了自由坐標系和統一坐標系中的兩套坐標數據。全站儀內置的自由設站觀測程序就可以利用這些基準點將所有點(包括測站點)的自由坐標轉換為統一坐標，通過對各點的周期性觀測，便可得到各變形觀測點的位移變化[4]。

2　全站儀測量位移和沉降精度估算

2.1監測點的點位誤差

將式(1)全微分，再根據誤差傳播定律[5]，可得監測點的坐標誤差：

(2)

其中,mS，mβ，mi,mv分別為全站儀測量斜距的中誤差、垂直角的中誤差、儀器高中誤差、棱鏡高中誤差。

2.2球氣差：由地球曲率和大氣折光引起的誤差

高程的測量受地球曲率c和大氣折光r的影響，其中：

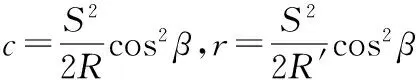
則有：

(3)

將式(3)全微分，再根據誤差傳播定律，可得球氣差引起的誤差：

mc-r=

(4)

其中，mK為大氣折光系數誤差[6]。

根據已有的實驗證明，當S<1 000 m時，大氣折光系數K在我國約為0.08～0.14，大氣折光系數誤差mK為±(0.3～0.5)[7]。在橋梁監測中，斜距一般不會很大，所以若斜距S≤300 m時，mc-r≈0，所以球氣差的影響可以忽略不計。

2.3儀器對中誤差、監測點偏心誤差、儀器高中誤差和棱鏡高中誤差

全站儀對中是采用儀器自帶的激光對中器或光學對中器，根據大量的現場實際經驗，當對中器和照準部水準器進行嚴格的檢驗校正后，儀器對中誤差在±1 mm內；當監測點采用三腳架和棱鏡基座安置棱鏡時，其偏心誤差和棱鏡高中誤差在±1 mm內，有m儀器對中=m偏心=mv=±1 mm[8]。

當建立具有穩定的觀測墩和具有強制對中裝置的棱鏡臺，那么儀器對中誤差和監測點偏心誤差以及棱鏡高中誤差都很小，可以不予考慮，即m儀器對中=m偏心=mv=0 mm[8]；在儀高測量中，采用游標卡尺在基座三個方向量取，使三個方向量取的校差小于0.2 mm，并在測前、測后進行兩次量測，使mi=0.2 mm，以此減少儀高測量的誤差[9]。

2.4多重自由設站時監測點沉降的點位中誤差

在應用全站儀測量坐標時，由于儀器的監測點的點位誤差、由地球曲率和大氣折光引起的誤差、儀器對中誤差、監測點偏心誤差、儀器高中誤差和棱鏡高中誤差之間相互獨立，因此根據誤差傳播定律，第一個自由設站點(自由設站點1)沉降的點位中誤差為：

(5)

其中，S1，i1，β1，v1，m儀器對中1，m偏心1分別為測量第一個自由設站時的斜距、儀高、垂直角、棱鏡高、儀器對中誤差、偏心誤差。

同理，根據誤差傳播定律，第二個自由設站點(自由設站點2)沉降的點位中誤差為：

(6)

其中，S2，i2，β2，v2，m儀器對中2，m偏心2分別為測量第二個自由設站時的斜距、儀高、垂直角、棱鏡高、儀器對中誤差、偏心誤差。

同理，監測點沉降的點位中誤差為：

(7)

其中，S3，i3，β3，v3，m儀器對中3，m偏心3分別為測量第三個自由設站時的斜距、儀高、垂直角、棱鏡高、儀器對中誤差、偏心誤差。

同理可以推導多重自由設站沉降的點位中誤差公式。

3　復雜基坑自由設站點和監測點的布置實例分析

3.1基坑自由設站點和監測點布置概況

茅臺4號大橋古藺岸為擴大基礎，基坑最大深度達到22 m。其現場施工圖如圖1所示。

從圖1可以看出，基坑周圍地形起伏很大，且有大量綠化植物。由于在穩定區域無法找到可以通視全部監測點的基準點，所以采用常規的方法無法對基坑的沉降進行監測。但在西側的房屋處有一處相對空曠場地，為此可以在房屋處布置兩個基準點1和基準點2，在基坑旁布置自由設站點1。但即便如此，利用基準點1也無法監測整個基坑，所以在自由設站點1的基礎上建立自由設站點2，這樣就建立了二重自由設站(兩個連續自由設站)，其設站和監測點布置圖如圖2所示。

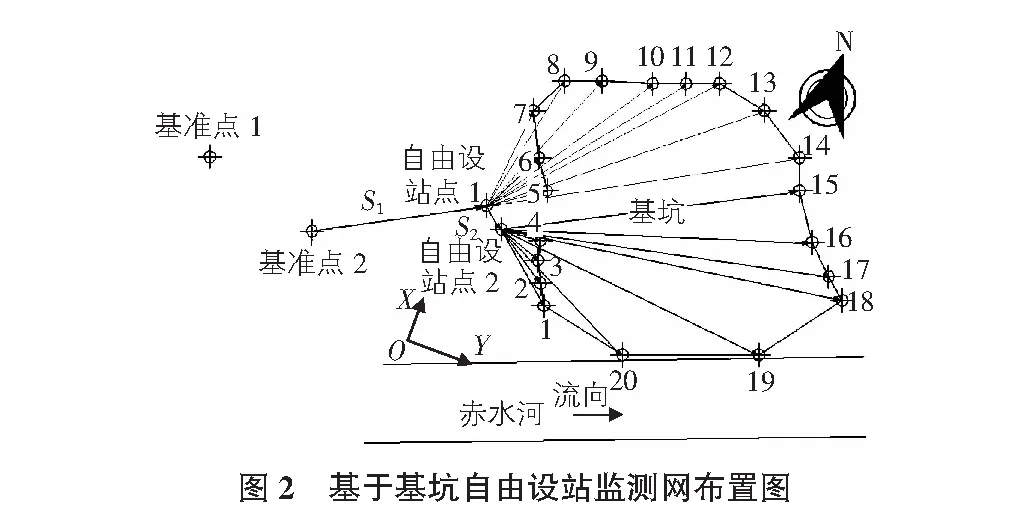
如圖2所示，為了能夠更加清楚的反映基坑的變形，對監測點的布置進行適當的加密。基準點1，點2布置于穩定區域，由于工程周邊地形的復雜與特殊性，本次測量只建立了兩個基準點。但在條件允許的情況下，一般應建立3個～4個基準點，這樣可以檢驗基準點是否穩定。自由設站點1、點2布置于基坑開挖影響范圍之內的場地。由于自由設站點的坐標會隨著基坑的開挖而發生輕微的變化，所以每次在進行測量之前都要對自由設站1和自由設站2進行校核。

3.2測量精度分析

由于篇幅的限制，這里選擇單一的徠卡TPS1200全站儀進行精度分析。根據儀器的標稱精度可知，其測角精度為±1.0 mm，測距精度為±(1.0 mm+1 ppm×S)，經過多次驗證統計，在人工照準目標200 m距離內，其實際角度測量精度mβ1=mβ2=mβ3=mβ=±0.38″，測距精度mS=±0.4 mm[10,11]。根據實際測量情況，兩個自由設站點的位置只會發生輕微的變動，為了便于分析，可以認為S1，S2在整個監測周期中保持不變，且有S1≈100 m，S2≈10 m，β1=20°,β2=0°，則mS1=mS2=±0.4 mm；為了提高精度，強制歸心裝置的觀測墩和棱鏡臺采用強制對中裝置，則有m儀器對中1=m儀器對中2=m儀器對中3=m儀器對中=0 mm，mi1=mi2=mi3=mi=±0.2 mm，m偏心1=m偏心2=m偏心3=m偏心=0 mm,mv1=mv2=mv3=mv=0 mm。代入式(5)可求得m1=±0.30 mm；同理代入式(6)可得m2=±0.4 mm。

結合式(7)，分析對不同斜距S和垂直角β以及在有強制歸心裝置的觀測墩和棱鏡臺采用強制對中裝置的情形下進行精度分析，如表1所示。

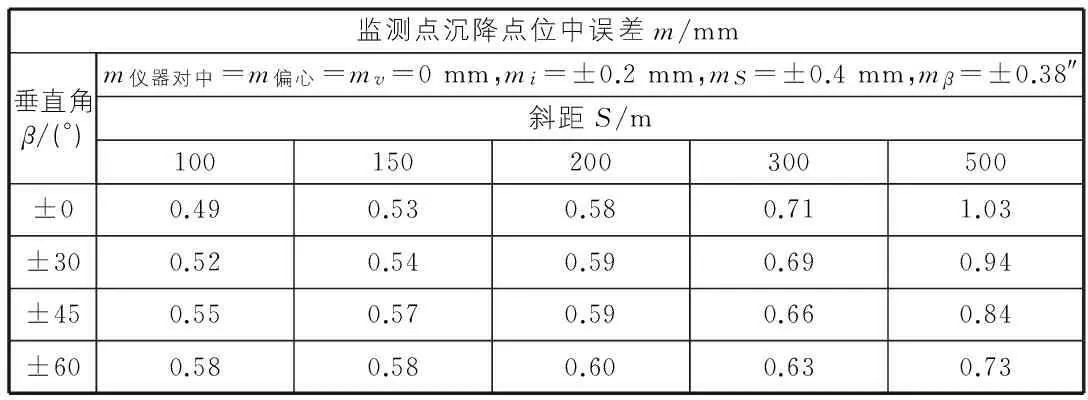
表1　在二重自由設站下監測點沉降精度分析

從表1中可以得出以下結論：

1)在斜距不大于300 m時,采用具有強制歸心裝置的觀測墩和具有強制對中裝置的棱鏡臺時，可以滿足基坑沉降三等精度的要求[10]；從表1中數據上看，在斜距不大于500 m時，也基本滿足三等精度的要求，但此數據是在200 m內mS=±0.4 mm，mβ=±0.38″的經驗數據上求得，所以在斜距為500 m時的精度被提高，不能滿足三等精度的要求。

2)在斜距不大于300 m時，沉降的精度隨著垂直角的增大而減小，大于300 m時，沉降的精度隨著垂直角的增大而增大。

3)以上精度分析數據表面，盡量選用低重自由設站，這樣可以提高測量精度。

4　結語

1)在基坑開挖形狀和周圍環境較為特殊，一個或多個獨立自由設站也無法對整個監測網實施監測時，可以考慮采用多重自由設站的方法來建立監測網，以對整個基坑進行實時監測。

2)全站儀基于多重自由設站的基坑沉降監測的方法，能有效解決基坑在特殊的地形和地物條件下，對于穩定基準點與監測點之間不能通視的問題。該方法測站擺放靈活，網形多變，能快捷的對整個監測網進行監測。

3)該工程最大斜距約為150 m，沉降監測按三等精度要求執行。沉降通過對二重自由設站水平位移監測精度的分析，采用徠卡TPS1200全站儀，具有強制歸心裝置的觀測墩和具有強制對中裝置的棱鏡臺，可以滿足沉降監測三等精度的要求。

4)為了能夠滿足精度的要求，多重自由設站的個數不宜較多，所以一般采用該方法確定1個～2個自由設站點較為合適。

[1]楊雪峰,劉成龍,羅雁文.基于自由測站的基坑水平位移監測方法探討[J].測繪科學,2011,36(5):153-154.

[2]駱旭佳,高飛,胡小華,等.全站儀自由設站在測繪中的應用[J].勘察科學技術,2010(1):44-45.

[3]王剛.全站儀結構原理與發展分析[J].現代建設,2013,12(10):34-36.

[4]劉沛.自動化全站儀在高層建筑基坑變形監測中的應用[J].測繪與空間地理信息,2011,34(3):239-141.

[5]武漢測繪科技大學測量平差教研室.測量平差基礎[M].北京：測繪出版社，1996.

[6]孔祥元,梅是義.控制測量[M].武漢:武漢大學出版社,2002:270-279.

[7]馮顯堂.大氣折光系數的取值[J].鞍鋼技術,1996(2):48-50.

[8]汪孔政.全站儀監測基坑水平位移精度分析[J].建筑技術,2009,40(2):153-154.

[9]晏紅波,黃騰,鄧標.智能全站儀精密三角高程測量替代二等水準測量[J].水電自動化與大壩監測,2007,31(4):43-46.

[10]GB 50026—2007,工程測量規范[S].

[11]王登杰,田文寶.基于差分技術的基坑位移監測方法研究[J].工程勘察,2015(2):79-84.

Research on the method of multiple free station based settlement monitoring of foundation pit

Luo BochengWu Haike

(CivilEngineeringCollege,GuizhouUniversity,Guiyang550025,China)

Introduced the principle of trigonometric leveling with total station instrument, and taking the Guling’an engineering of Maotai No.4 bridge as an example, analyzed the total station measuration displacement and settlement precision and the corresponding measuring instruments are selected to achieve the purpose of real-time, fast and accurate response of foundation pit.

complex foundation pit, multiple free station, settlement monitoring, monitoring point

1009-6825(2016)23-0066-03

2016-06-07

羅伯成(1989- )，男，在讀碩士；吳海科(1990- )，男，在讀碩士

TU433

A