“數與形”教學研究報告

漣源市小學數學研究會瀟湘數學教育工作室

“數與形”教學研究報告

漣源市小學數學研究會瀟湘數學教育工作室

一、對數形結合思想方法的理解

數學是研究現實世界空間形式和數量關系的科學。數學的許多問題都是圍繞數和形的提煉、演變、發展而展開的。在數學上，我們把根據數與形之間的對應關系，通過數與形的相互轉化來解決數學問題的思想方法叫做數形結合。小學數學教材一直都很重視對數形結合思想方法的滲透與運用。幾乎從第一節課認識數字開始，學生就受到數形結合思想方法的熏陶。

人教版新教材在六年級上冊安排了數與形為主題的教學，讓學生有機會走近、理解并運用數形結合的思想方法。這一內容呈現在“數學廣角”版塊中，集中發揮了它在培養學生的思維能力上的優勢——由數思形，培養思維的靈活性；由形思數，培養思維的縝密性；數形結合，培養思維的創造性；數形對照，培養思維的批判性。這種抽象思維與形象思維有機結合時，能促使學生多方位、多角度、多層次地思考問題，進而培養他們靈活、深刻地分析問題與解決問題的能力。

二、教學中存在的問題及分析

（一）教學實踐中的問題

因為這是教材新增的內容，可供參考的文獻資料不多，無形中給教學增加了難度。實際教學中，數學老師對數形結合的思想方法了解多少？在具體的操作中，又是如何落實這種思想與方法的呢？對此，我們在全市抽取了40名小學數學教師和40名六年級學生作為樣本進行了問卷調查。調查結果顯示，大多數教師對數形結合基本含義的理解多集中于一些具體現象，對功能性含義關注不夠；認為數學思想方法在教學目標中是隱性的，想滲透但不知怎樣滲透；教學時關注了以形助數，對以數解形重視不夠。學生只有少部分聽說過數形結合的思想方法，主動用數形結合的方法解決問題的經驗明顯不足。由此可見，數形結合的思想方法還沒有真正落實到小學數學課堂教學中，老師們普遍重視不夠，數學思想方法的教學是不到位的。

1.如何合理地定位教學目標。在舊教材中，例2及后面的幾道練習題都屬于思考題甚至競賽題，而新教材把這些內容作為主體內容進行教學，那么這部分內容在教學時究竟要達到怎樣的要求呢？

2.如何精選教學材料。課后練習題里編入的習題哪些能讓學生真正感悟數形結合的思想方法？需要補充哪些學習材料讓學生體會數形結合的優越性？

3.如何選擇有效的教學策略。這部分內容的教學難度較大且相對獨立，教學時如何搭建腳手架，既能讓學生夠得著又能夠避免教師硬給？

4.如何讓學生較好地感悟極限思想。教材中例2的內容體現了極限思想。極限思想作為一種數學思想，小學生理解起來會覺得比較抽象。教材也試圖借助形直觀形象地解釋的結果就是1。這樣的處理，學生對結果1的理解是否有困難？教學時如何創設合適的情境，讓學生感悟極限思想？

1.學生常常把畫線段圖、作圖等借助幾何圖形簡化代數思考的過程看成是老師加在他們身上的負擔，體會不到數形結合方法的精妙。

2.數形結合大致可以分為以形助數、以數解形兩大類。由于小學生年齡、知識的局限，數形結合在小學階段更多地表現為以形助數，以降低思維難度。也因為小學階段學生接觸的大多是具體的數據，用字母表示數的內容較少，往往難以滿足以數解形教學的需要。

（二）對問題的分析

1.抓住問題情境和數學思想方法之間的結合點

如果教師用心琢磨，就會發現數形結合思想在數學教學中無處不在。教師教學時，要善于發現，充分挖掘問題情境中隱含的數學思想方法，找準數學思想方法與問題情境之間的結合點，利用數形結合思想幫助學生在形象思維和抽象思維之間搭建橋梁，讓學生在學習數學、理解數學的過程中感悟數學思想方法，發展思維能力。

2.如何提升學生運用數學思想方法解題的素養

對學生而言，如果能充分感受數形結合思想方法在數學學習中的價值，并將數形結合的思想遷移到解決其他一些實際問題，對他們形成良好的思維素質與技巧，提升數學能力是大有裨益的。所以，問題的關鍵還在于教師如何把教學內容中隱含的數形結合思想方法顯性地傳遞給學生，把學生潛在的關于數形結合思想方法的經驗激活。教師的教學需要在這方面下功夫。

三、教學實踐

片段一：

教師板書一列數：1，4，9，16，（）。

師：猜猜看，接下來的這個數會是什么呢？說說你的想法。

生1：這列數中相鄰兩數之間依次相差：3、5、7，是連續的奇數，接下來應該加9，所以這個數應該是16+9=25。

師：同學們聽明白了他的意思嗎？誰還有不同的發現嗎？

生2：我發現這些數都是平方數。第一個數是1的平方，第二個數是2的平方，第三個數是3的平方，第四個數是4的平方，所以我猜第五個數是5的平方，應該填25。

師：看到這些平方數，你能馬上聯想到我們熟悉的哪個圖形呢？

生3：正方形，正方形的面積就是邊長的平方。

師：棒極了！難怪平方數又叫正方形數呢。看來，數與形之間有著一些奇妙的聯系，這節課我們就一起來研究“數與形”（板書課題）。

師：有意思的是，在上面的同一組數據中，同學們找出了兩種不同的規律，這又是為什么呢？帶著這個疑問，我們一起走近這個奇妙的正方形吧。（出示圖1）你能一眼看出這是多少個小方格嗎？是怎么知道的？

生4：25個小方格，用5×5=25。

師：不錯，25就是5的平方數。現在的問題是，這些小方格的個數除了用5×5計算外，還有沒有別的算法？也許你會覺得這個問題很奇怪，除了用5×5計算，還能有什么好辦法呢？數學就是這樣有意思，有時候我們換個角度思考就會有不一樣的發現。剛才我們不是在同一組數據中發現了不同的規律嗎？現在，你換個角度看看這幅圖，怎么看就能看出每次加3、加5、加7……這樣的規律呢？

圖1

學生思考。

生5：我是拐著彎進行計數求和的，第一層1個，第二層3個，第三層5個，第四層7個，第五層9個，那么25=1+3+5+7 +9。（課件相機演示，如圖2）

師：咦，加一層不就是加一行一列嗎？一行2個，一列2個，兩個2不是4嗎？為什么這里只加了3個？

生6：看圖就會發現，拐角上的這個方格在行里數到它，在列里又數到它，重復了一次，減去1，就只有3個了！

師：噢，我明白了！數形結合就是這么奇妙！（動畫演示：依次遞加一層）

圖2

生7：3+3-1加了5個，4+4-1加了7個，5+5-1加了9個。

師：每加一層，正方形的邊長就多1，1+3+5+7+9構成了5×5的正方形！剛才我們從不同的角度研究了同一個圖形，找到了兩種不同的算法，一種是5× 5，另一種是1+3+5+7+9，若綜合這兩方面考慮，這兩個算式之間可以用什么符號聯結？

生：等于號。（板書：5×5=1+3+5+7+9）

師：大家大膽地想象一下，如果我們在這個正方形的外面再加一層，這個等式會怎么變？

生8：6×6=1+3+5+7+9+11。

師：真好！我們再大膽地想象一下，有一個正方形的小方格數可以寫成這樣一個算式：1+3+5+…+99，那是多少個小方格的正方形呢？

學生交流討論。

生9：我們找到了規律，這個算式有多少個加數，小方格的個數就是這個加數個數的平方數。100以內的奇數有50個，這個正方形的小方格數就是50× 50！

師：數學真奇妙，換個角度看一看，竟然有了這么多的發現！同學們，如果再換個角度觀察這個正方形，你還會有新的發現嗎？

學生獨立思考后進行同桌交流。

生10：我們發現斜著看也很有意思（如圖3），1+2+3+4+5+4+3+2 +1。

師：太棒了！斜著看，誰還有不同的發現？

生11：斜著看，每次多了1個小方格，加到5以后，每次又少1個小方格，5是最大數，5的左右兩邊是對稱的。

圖3

師：你們的表現真不錯！正因為這種對稱，才使得這些小方格拼成了一個5×5的正方形。同學們大膽地猜想一下，如果這個最大數是6呢？1+2+3+4 +5+6+5+4+3+2+1又會是幾行幾列的正方形呢？

生12：6行6列，有36個小方格。

師：看樣子，同學們在數與形中找到了規律。回顧剛才的研究歷程，我們從兩個不同的角度研究了同一個圖形，發現1+3+5+7+9和1+2+3+4+5+4 +3+2+1都可以表示5行5列的大正方形中小正方形的個數。怎么樣？數學有意思吧？剛才這些有意思的發現都源于一個非常簡單的圖形——正方形。我們都要感謝它！難怪數學家華羅庚也曾這般感嘆：“數缺形時少直觀，形少數時難入微；數形結合百般好，隔離分家萬事休。”數形結合的方法如此之好，不如老師給一個問題，你們也來體驗體驗數形結合的妙處吧。（課件出示：

生13：分母有規律呢，后一個加數的分母總是前一個加數的分母的2倍。

師：嗯，很重要的發現！

生14：如果通分再計算的話太難了，肯定有簡便算法的吧？

師：尋求簡便算法是一條很好的思路。問題是，你沒有這類題的解題經驗的時候，如何找到這個方法就顯得特別重要了。華羅庚先生說過這么一個方法，不知道對同學們尋求方法有沒有幫助——我們要善于退，足夠地退，退到原始而不失重要性的地方，退到我們容易看清問題的地方。對這個問題，我們要退到什么地方比較合適呢？

生15：先計算兩個數相加，然后每次加一個數看看。

師：對，摸著石頭過河，大家試試看吧。

學生獨立計算，小組交流、展示。

生16：我是一個一個加的，得數好像有點規律。

生17：得數的分子總是比分母少1。

生18：得數的分母和最后一個加數的分母是一樣的。

生19：我知道了，這樣加下去的話，結果的分母是最后一個加數的分母，分子總比分母少1。

生20：我也知道了這道題的結果

師：這是一個很有意思的結果，老師很欣賞大家學習數學的方法。我們面臨一個新的問題時，尋求解決問題的方法很重要。前面我們學習了數形結合的方法，你能找到一個合適的形表示這個加法算式的意思嗎？

生21：我用一個正方形表示的。正方形的一半是

圖4

師：這個形很生動地解釋了這個結果。同學們可以大膽地想象，加的數越多，這個結果越接近1。除了正方形，你還能想到別的形嗎？

生：長方形！圓形！線段！

師：（課件相機出示，如圖5）有道理！雖然形各不相同，但說明的數理是一樣的。而且我們不難發現，像這樣比較復雜的問題，畫圖的確是個解決問題的好方法！

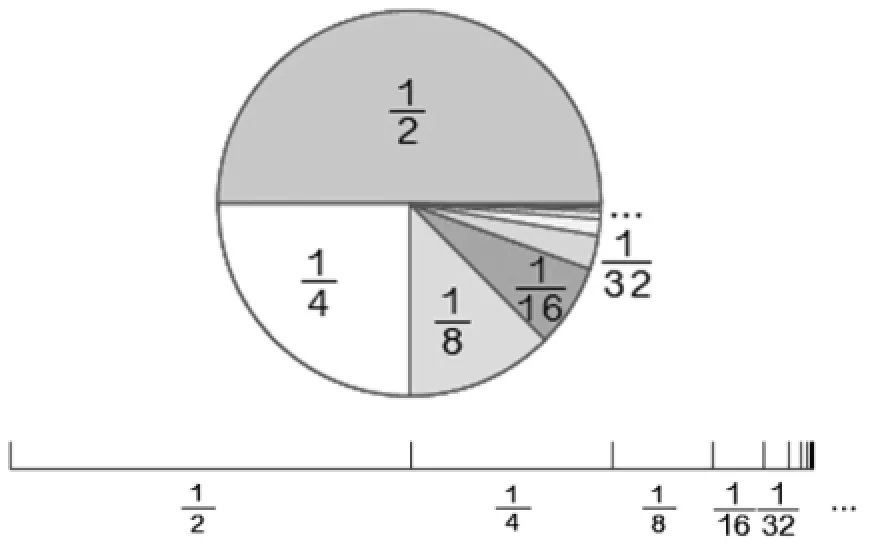
圖5

教學意圖：這一片段的設計體現數形結合中以形助數的一般特征和解題優勢，實現了數學問題中數與形的溝通，使學生初步了解了數與形之間的緊密聯系，掌握了數與形進行轉化的方法，提升了應用數形結合思想解決數學問題的意識，發展了數學思維的靈活性。

片段二：

師：孩子們，在前面的學習中，大家都有了不起的表現。在形的幫助下我們解決了有關數的難題（板書：以形助數）。其實，數與形真是一對好朋友，數形結合除了以形助數外，數對形的幫助也同樣重要。這節課我們一起研究以數解形（板書：以數解形）。研究從一道有意思的數學題開始。（課件出示圖6）如圖，長方形ABCD被線段EG和FH分割成4個小長方形，其中長方形BEOF的面積為30平方厘米，長方形CGOF的面積為20平方厘米，長方形DGOH的面積為12平方厘米，求長方形AEOH的面積。

學生先獨立思考，然后同桌交流再匯報。

生1：我們覺得要求長方形AEOH的面積，就需要找到它的長和寬，但是題目只給了另外幾個長方形的面積，并且這幾個長方形的長和寬都沒有確定，我們沒有找到解決問題的辦法。

師：你們雖然沒有找到解決問題的辦法，但清楚地表達了自己思考問題的過程以及困惑，也不錯。

生2：我們覺得面積是30平方厘米的①號長方形和面積是20平方厘米的②號長方形有一條公共的邊，這條邊的長度應該是這兩個數的最大公因數，所以是10厘米，另外兩條邊分別是3厘米、2厘米，而這個3厘米和2厘米同時也是④號長方形和③號長方形的一條邊長，③號長方形的另一條邊的長度是6厘米，也是④號長方形的一條邊長，這樣，④號長方形的面積就是3×6=18（平方厘米）。（如圖7所示）

師：這位小老師很有范兒，一邊表達自己組的觀點，一邊用數描繪了這個長方形面積的計算過程，你們對他的發言有什么意見嗎？

生3：他講得好像有點道理，但是①號和②號長方形的那條公共邊的長度一定是它們的最大公因數嗎？

師：這問題提得非常有價值！是啊，如果這條公共邊不是最大公因數，還有可能是哪些數呢？

生4：可能是2，也有可能是5！生5：還有可能是1呢！

生6：說不定是個小數呢。

師：要不你們各自選一個可能的數，算一算④號長方形的面積吧。

圖6

圖7

學生獨立運算后交流。

生7：我把①號和②號長方形的公共邊看成5厘米，算出④號長方形的面積仍然是18平方厘米。（如圖8所示）

生8：我把①號和②號長方形的公共邊看成2厘米，算出④號長方形的面積仍然是18平方厘米。（如圖9所示）

師：問題研究到這里，你們有什么疑問嗎？

生9：看上去，只要是已知的3個長方形的面積不變，邊的長短不影響問題的結果，這是為什么呢？

師：會提問題的小朋友一定是最會思考的！是啊，這是為什么呢？

學生再一次陷入沉思。

生10：我想，既然邊的長短與問題的結果沒有關系的話，我們用字母表示應該也可以啊，這個字母想代表幾都是可以的。

師：你說的有道理，下面我們把OE，OF，OG，OH的長度分別記作a，b，c，d（如圖10所示），算一算這些長方形的面積，你又

發現了什么？

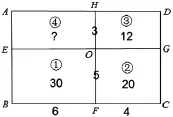
圖8

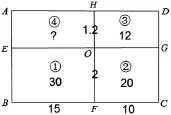
圖9

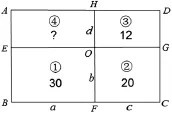
圖10

生11：從圖形中我們可以看出a×b=30（1），b×c=20（2），c×d=12（3），問題是求a×d=？這里的a和d在算式（1）和算式（3）中，而且要算乘積，我們可以把算式（1）和算式（3）乘起來，a×b×c×d=30×12=360，其中b×c是20，那a×d就是360÷ 20=18！

師：多么了不起的研究！用字母表示數，解開了一個大謎團！事實上，在一個乘法算式里，在積不變的情況下，一個因數擴大幾倍，另一個因數一定會縮小幾倍。④號長方形的面積就是由兩個這樣的因數相乘得來的，面積難怪總是固定的。

生12：老師，上面的算式（1）和（3）

相乘的結果就是①號和③號長方形的面積的積，是a×b×c×d，其實②號和④號長方形的面積的積也是a×b×c×d！

師：你發現了對角線上的兩個長方形的面積的乘積相等，真了不起！

生13：早知道這樣，我們只要用①號和③號長方形的面積之積除以②號長方形的面積就可以算出④號長方形的面積了！

師：真是茅塞頓開啊！在解決這個問題的過程中，邊長和面積對應的數給了我們那么多的啟發。在這些數的幫助下，我們深入地研究了這幾個長方形面積，發現了這幾個長方形之間的奇妙聯系。我們不得不說，數形結合百般好啊！

教學意圖：這一片段的設計體現數形結合中以數解形的一般特征和工具性作用，實現了數學問題中數與形的溝通。學生初步了解了數在對形的本質屬性探究中的意義，認識到相對于以形助數的技巧性，以數解形具有更強的工具性和普遍性。特別值得一提的是，在教學過程中，教師從學生思考問題最自然的路徑出發，滲透了從特殊到一般的思想方法，讓學生經歷了從特殊到一般的歸納推理過程。

四、不得不說的后話

數與形的教學，當然要關注數形結合，而數形結合離不開以形助數與以數解形這兩個方面。既然作為一個專題出現在“數學廣角”版塊，如果只滲透以形助數的方法，我們認為是不全面的。教師通過對教材的理解，開發出能夠體現這兩個方面的教學內容，讓學生對數形結合的兩個方面都有所了解，為后繼學習（特別是中學階段的解析幾何的學習）鋪路是很有必要的。為此，我們對教材作了以下幾方面的處理。

1.教材中的學習材料強調了對一個圖形進行研究，從不同的角度分析它、計算它，就可能得到新的結論（數學家富比尼稱之為“算兩次”）。比如，從1開始連續幾個奇數之和恰好是一個自然數的平方。這當然是研究問題的重要方法。但問題是，學生如何理解“為什么要對同一幅圖算兩次”呢？為了讓學生思考問題有更自然的路徑，我們補充設計了“給一組數據找規律”的問題。學生在教師的引領下嘗試從不同角度觀察同一圖形，發現數與形的奇妙聯系，然后呈現教材中的幾個學習材料，學生對形之于數的作用就有了深入的理解。

3.片段二的學習材料是教材中沒有的，我們之所以利用它來教學，源于這么幾個思考。一是這個材料的確能讓學生體會到以數解形的工具性，隨著學生假設的數據不斷呈現，規律慢慢地被揭示。這種發現的驚喜應該是學生思考獲得的獎賞。二是這個材料的選取具有開放性。在對問題的討論中，當結論集中指向一點時，學生在不經意間經歷了由特殊到一般的歸納推理過程。而在課堂教學中滲透數學思想與方法是我們一直以來的追求。事實上，學生在整個學習過程中情緒飽滿，始終處于“火熱的數學思考”中，課堂也因此成為讓思考發生的樂園。

數形結合在小學階段更多地表現為以形助數，用字母表示數的內容較少，故往往難以滿足以數解形教學的需要。事實上，隨著學生思維能力的發展和數學知識的積累，以數解形在中學階段將大放異彩。尤其在學習了函數、解析幾何等知識后，數學學習才真正進入以數解形的快車道。那么，如何讓小學生體會到這一點，尋找以幾何內容為出發點，因形尋數，將直觀的圖形與抽象的代數語言結合起來，并容易被小學生所接受的素材成為我們研究的新問題。（本文系湖南省教育科學“十二五”規劃立項課題（課題批準號：XJK014CZXX041）《以小課題研究促進小學數學教師專業成長的研究》的階段性成果）

（執筆：王麗燕、謝加文、劉碩鵬、唐紅霞、肖石堅、徐旺、李闖）