球的接、切問題處理策略

安徽省太和中學 岳峻 韓長峰

球的接、切問題處理策略

安徽省太和中學 岳峻 韓長峰

從2016年起，安徽省高考不再是自主命題，而是采用全國Ⅰ卷，這是挑戰，其中的一個挑戰包括球的接、切問題。近十年安徽省自主命題一般不考查此類問題，但是這在全國Ⅰ卷屬于必考知識點。作為一個不可小覷的考點，我們要了解球的概念，掌握球的性質，掌握球的表面積公式、體積公式，從而解決與球的截面有關的問題。

下面就球的接、切問題進行分類探討，并給出相應的解決對策。

一、考查球的表面積、體積

策略 關鍵是由已知球的接、切信息的幾何特征探求球的半徑，然后代入相應的公式S球=，求解球的表面積和體積。

例1 設球的體積為V1，它的內接正方體的體積為V2，下列說法最合適的是（ ）。

A.V1比V2大約多一半 B.V1比V2大約多兩倍半

C.V1比V2大約多一倍 D.V1比V2大約多一倍半

評注 本題利用球的直徑亦即內接正方體的體對角線這一知識點，建立等量關系求得兩個幾何體的內在聯系。

二、考查球的截面的性質

策略 球心與球的截面圓的圓心的連線垂直于該截面圓，球心與球面上任意一點所連的線段都是球的半徑。這些性質是解決球的接、切問題過程中化空間為平面的根本依據。

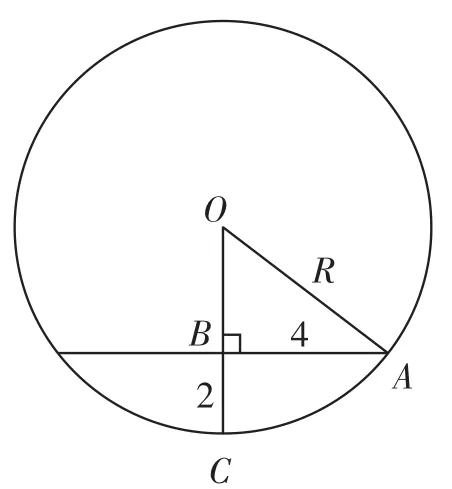
例2 已知A、B是球O的球面上兩點，∠AOB=90°，C為該球面上的動點，若三棱錐O-ABC體積的最大值為36，則球O的表面積為（ ）。

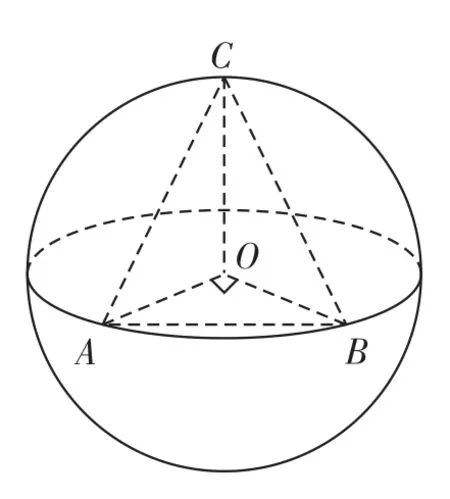
A.36π B.64π C.144π D.256π

解析 如右圖所示，當點C位于垂直于平面AOB的直徑端點時，三棱錐O-ABC的體積最大。設球O的半徑為R，此時

解得R=6，所以球O的表面積為S=4πR2=144π。故選C。

評注 本題求三棱錐O-ABC體積的最大值時，靈活地借助于三棱錐的特性轉化為求三棱錐C-AOB體積的最大值，是一個很好的策略。

例3 如右圖所示，半徑為R的球O中有一內接圓柱。當圓柱的側面積最大時，球的表面積與該圓柱的側面積之差是。

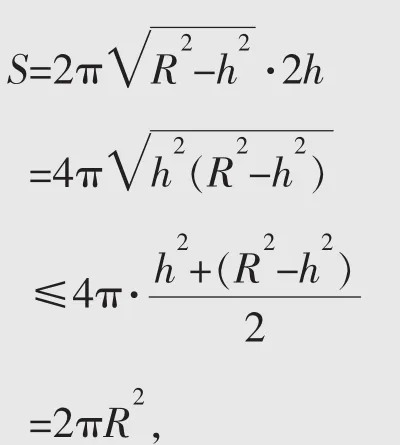
當且僅當h2=R2-h2，即2h2=R2時取等號。

故圓柱側面積的最大值為2πR2。

此時球的表面積與該圓柱的側面積之差是4πR2-2πR2=2πR2。故填2πR2。

評注 本題運用已知信息及圓柱體的有關性質，建立圓柱體側面積關于球半徑R的關系式，靈活應用基本不等式，求得圓柱的側面積最大時R與圓柱體高h的關系。

三、考查與球有關的組合體

策略與球有關的組合體問題，一種是內切，一種是外接。解題時要認真分析圖形，明確切點和接點的位置，確定有關元素之間的數量關系，并作出合適的截面圖，常見的一些軸截面圖如下：

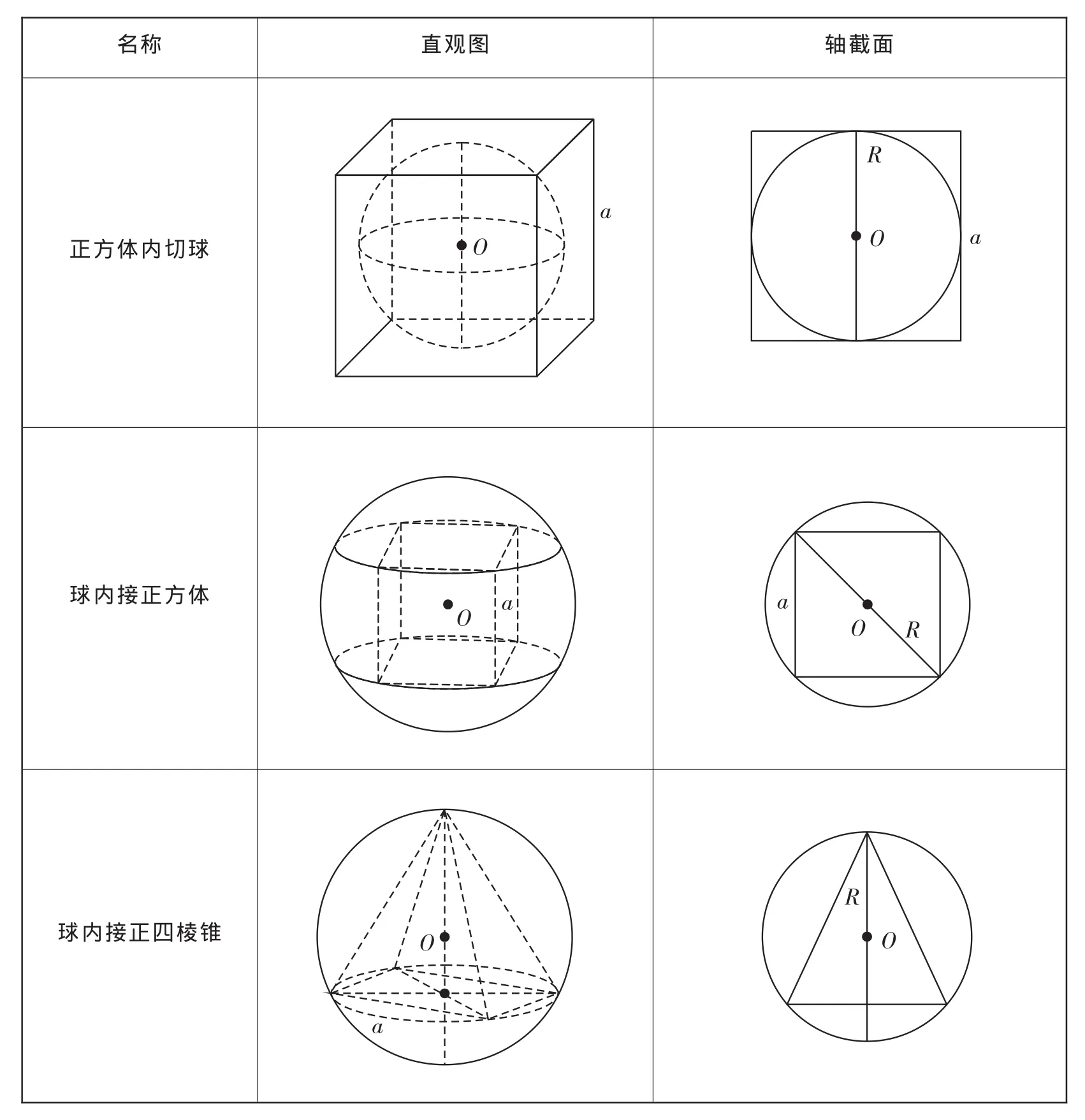
內切問題的關鍵是抓住相切時的實質，即球心到切點的距離等于球的半徑；外接問題的關鍵是抓住相接時的特征，即球心到接點（多面體的頂點）的距離等于球的半徑。

例4 正四棱錐的頂點都在同一球面上，若該棱錐的高為4，底面邊長為2，則該球的表面積為（ ）。

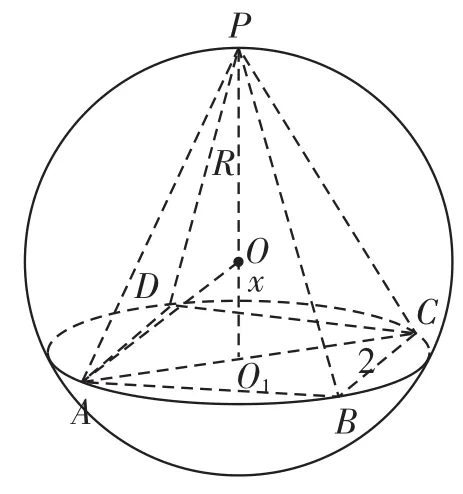
解析 如右圖所示，設O為球心，PO=OA=R，OO1=x，

評注 本題巧妙運用正四棱錐的性質，確定其外接球的球心在它的高PO1上，進而建立直角三角形，解出球的半徑，再求出球的表面積。

例5 如右圖所示，有一個水平放置的透明無蓋的正方體容器，容器高8 cm，將一個球放在容器口，再向容器內注水，當球面恰好接觸水面時測得水深為6 cm，如果不計容器的厚度，則球的體積為（ ）。

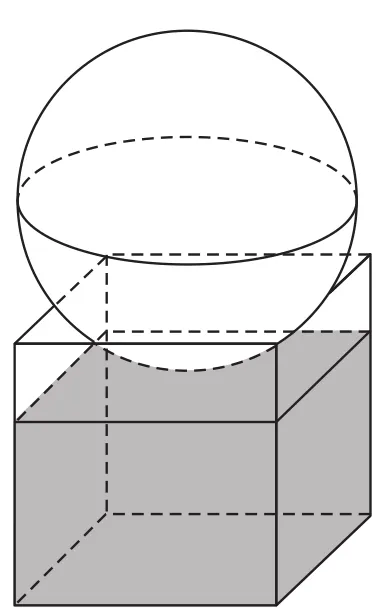
解析 設球的半徑為R，則由題知，球被正方體上底面所在平面截得圓的半徑為4，球心到截面圓的距離為R-2，球平行于正方體側面的軸截面如右圖所示，△OBA為直角三角形，

則R2=（R-2）2+42，解得R=5，

評注 球與多面體間的“切”的問題，關鍵突破口是作出過它們的切點且與軸截面重合的一個截面，將空間問題轉化為平面問題解決，在計算過程中要抓住球半徑這個主要元素。

解析 如右圖所示（部分線段未畫出），設球心為O，正方形ABCD的中心為O1，

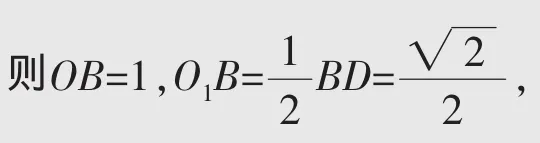
易知SO2為線段OO1的垂直平分線，所以SO1=SO=1。故選C。

評注 解決球與其他幾何多面體間的“接”的問題，關鍵在于仔細觀察和分析，弄清相關元素的幾何關系和數量關系，選準最佳角度作出截面，使這個截面盡可能多地包含球、幾何體的各種元素以及體現這些元素之間的關系，達到空間問題平面化的目的。

例7 正四面體的內切球、與棱相切的球、外接球這三類球的半徑之比為。

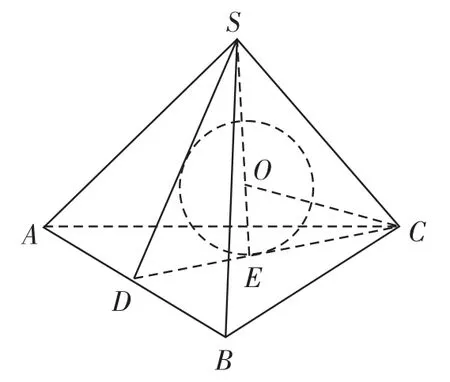
解析 設正四體的棱長為1，外接球和內切球半徑依次為R、r，由正四面體三個球心重合及其特征，則正四面體的高

評注 正四面體的棱長為a，高為h，外接球、內切球的半徑分別為R、r，相鄰兩個表面所成的角為θ，則，其推導方法中隱含著等體積變換和分割法。如果將正四面體納入正方體中得到其伴隨正方體，正四面體的體積等于其伴隨正方體體積的，正四面體的外接球和其伴隨正方體的外接球是同一個球，正四面體的棱長等于其伴隨正方體棱長的倍。利用這種伴隨關系可以簡化求正四面體的有關問題。

例8 設三棱柱的側棱垂直于底面，所有棱的長都為a，頂點都在一個球面上，則該球的表面積為（ ）。

解析 過三棱柱的側棱AD及球心O作一平面截球，得如圖所示的平面，設點G為正三角形ABC的中心，連接AO、OG，則OG⊥AG，

四、考查與多球有關的接、切

策略解決此類問題的關鍵是抓住球與球之間的連心線的長是兩球半徑的和。

例9 將半徑都為1的4個鋼球完全裝入形狀為正四面體的容器里，這個正四面體的高的最小值為（ ）。

解析 由題意，四個半徑為1的小球的球心O1，O2，O3，O4恰好構成一個棱長為2的正四面體O1-O2O3O4，并且各面與正四面體容器P-ABC的各對應面的距離都為1。

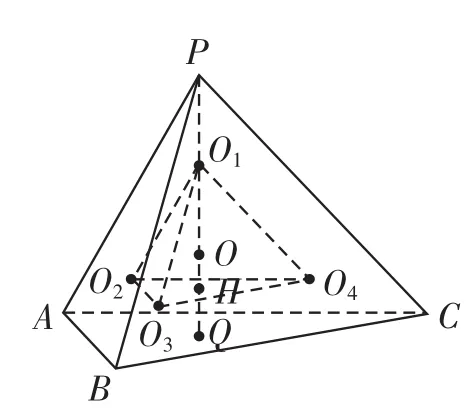
如圖所示，正四面體O1-O2O3O4與P-ABC是有共同的外接球球心O的相似正四面體，從而有，

又HQ=1，所以O1P=3，由于

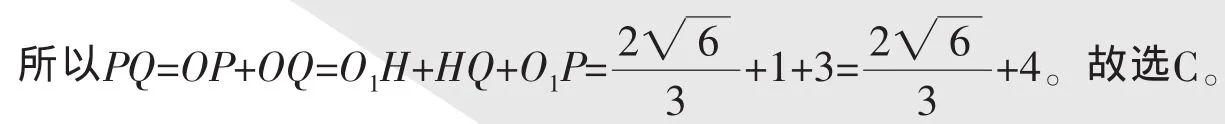
由于“球”是“圓”在空間概念上的延伸，所以研究球的性質時，應注意與圓的性質類比。球的軸截面是大圓，它幾乎含有球的全部元素，所以針對有關球的計算，往往可以作出球的一個大圓，化“球”為“圓”來解決問題；在解決與球有關的“切”“接”問題時，一般要過球心及多面體中的特殊點或線作截面，把空間問題轉化為平面問題，從而尋找幾何體各元素之間的關系。總之，只要發揮好空間想象力，借助于數形結合進行合理轉化，所有問題便可迎刃而解。