求解含小阻抗支路配電網潮流的牛頓法

初　壯，于群英，李笑薇

（1.東北電力大學電氣工程學院，吉林 132012；2.國網吉林省電力有限公司電力科學研究院，長春130000；3.吉林省送變電工程公司，長春 130000）

求解含小阻抗支路配電網潮流的牛頓法

初壯1，于群英2，李笑薇3

（1.東北電力大學電氣工程學院，吉林 132012；2.國網吉林省電力有限公司電力科學研究院，長春130000；3.吉林省送變電工程公司，長春 130000）

基于節點導納矩陣的雅可比矩陣為病態，是采用牛頓法求解含合環支路等小阻抗支路的配電網潮流不易收斂的主要原因。文中以等效負荷支路、合環支路分別為連支建立兩類基本回路，潮流方程基于回路電流-負荷節點電壓方程建立，合環支路參數不會作為回路矩陣的獨立元素存在；采用牛頓法求解時，基于回路導納矩陣建立良態的雅可比矩陣，使計算收斂性得到保證。多個算例驗證了該方法在計算含合環支路和PV節點配電網潮流時的正確性和有效性。

配電網潮流計算；收斂性；回路分析；牛頓法；小阻抗支路

典型的傳統配電網是單一電源供電的輻射狀網絡。而現代配電網構成日趨復雜：風力、光伏發電等分布式電源的大力發展改變了配電網單一電源供電模式［1-6］；而實際運行時會出現閉合分段開關和聯絡開關的情況，使配電網呈現為弱環網［6］。潮流計算是電力系統運行分析的基礎，配電網潮流計算需要面對這些新問題。前推回代法在求解傳統配電網潮流時具有簡捷、高效的特點，但不能直接用于弱環網或電網具有PV節點的情況。因此，文獻［7-8］采用疊加原理來處理環網問題，文獻［5-6］在迭代中采用不同方法對PV節點進行電壓修正。這些修正使前推回代算法的效率有所降低。

牛頓法易于處理多電源節點和復雜網絡結構，廣泛用于輸電網潮流計算；但配電網潮流采用牛頓法時，網絡中合環開關等小阻抗支路［9］的存在使算法收斂性有很大程度下降。對牛頓法計算含小阻抗支路的輸電網潮流收斂性較差的原因與解決方法已有較多研究：文獻［10-11］指出，小阻抗支路的存在使潮流方程雅可比矩陣呈現病態，使迭代過程不收斂；文獻［10］指出提高程序計算精度可以提高算法收斂性；文獻［11］通過改變迭代過程電壓初值提高收斂性；文獻［12］則采用線性變換對雅可比矩陣進行預處理等。配電網多呈輻射網或弱環網運行，R/X較大，小阻抗支路數量要多于輸電網，這些特點使牛頓法在計算基于節點形式潮流方程時更加不易收斂［9］。

本文采用牛頓法計算基于回路形式配電網潮流方程。采用回路形式潮流方程，不但可有效處理弱環網，更重要的是可避免出現病態的雅可比矩陣；牛頓法的應用則使算法可直接用于含PV節點的配電網，對含分布式電源配電網有良好的適應性。

1　基于回路分析的配電網潮流方程

1.1回路的形成和分類

對于帶有環路的配電網，按如下規則建立回路電流方程：斷開形成環路的支路，則配電網呈輻射狀，此時，將各節點負荷或分布式電源視為接地支路，則自根節點至負荷節點或分布式電源所在節點的對地支路可形成回路，取回路電流為負荷節點或電源節點對地的注入電流，稱其為第1類回路；取回路電流為負荷節點對地的注入電流，對應的回路方程稱為第1類回路方程；將形成環路的支路接入配電網，則自根節點至該支路一個關聯節點、經由該支路至另一關聯節點并由另一節點回溯至根節點也會形成回路，稱其為第2類回路；取回路電流為環路支路電流，方向規定為由節點編號大的節點指向編號小的節點。

配電網輻射狀運行時，各線路皆為樹支，而節點負荷投入或合環支路閉合則會使配電網中出現回路；負荷等效支路、合環支路都是連支，但它們性質不同，因此，把由它們的出現而產生的回路分別定義為第1類和第2類回路。

例如，圖1是一個8節點（未計入接地點）、9條支路的配電網絡，其中支路b11、b12是合環支路。另外，有1、3、6共3個節點接負荷，可看作3條支路b8、b9、b10；根節點與接地節點之間可看作為一條電壓源支路，記為b0。通常的配電網絡的支路概念中不含b0、b8、b9、b10這些支路。

對應支路b8、b9、b10，有3個第1類回路：

loop 1-1：b0-b1-b3-b6-b8；

loop 1-2：b0-b1-b4-b7-b9；

loop 1-3：b0-b2-b5-b10。

對應兩個合環支路b11、b12，有兩個第2類回路：

loop 2-1：b3-b11-b4；

loop 2-2：b1-b12-b2。

然后，消去第2類回路（下文詳細說明），可以得到關于1、3、6共3節點的方程，求取得到帶有負荷節點的參數，然后根據支路方程求取不帶負荷節點的參數，進而得到所有節點參數。同樣，對于8節點系統，如果每個節點都帶有負荷，則經消去第2類回路可建立含有8個方程的方程組，可直接求出每個節點的參數。

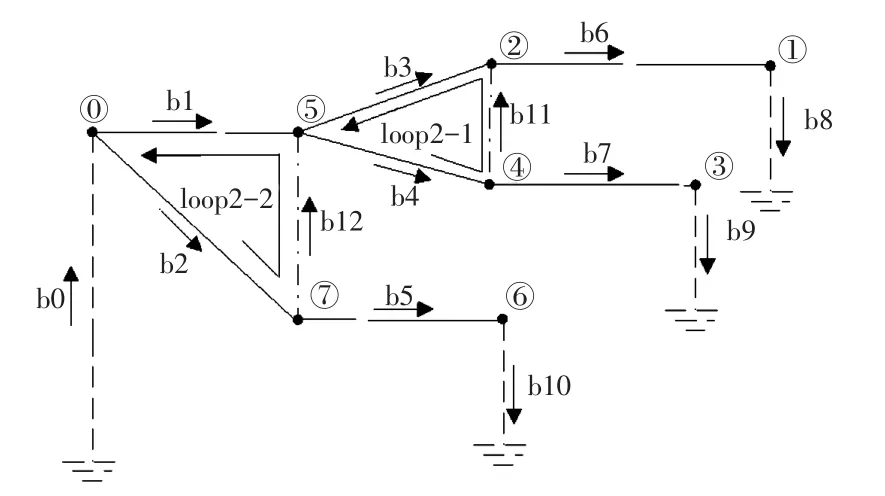
圖1　兩類回路的劃分Fig.1 Two types of loops

1.2分布式電源的處理

目前，比較成熟的分布式電源主要有光伏、風力發電機、燃料電池、微型燃氣輪機。對于光伏可根據其無功功率與有功功率、電流、節點電壓的關系，將其轉化成PQ節點處理［4］；雙饋風力發電機可直接等效成功率方向相反的負荷；而對于燃料電池，微型燃氣輪機，在潮流計算時會被處理成PV節點［4］。對于PV節點來說，無需計算關于其無功功率的方程式，其有功功率的不平衡量以及對應的雅可比矩陣元素與PQ節點相同。

1.3回路方程的建立

本文中將第1類回路方程連續排列在先，第2類回路方程連續排列在后，則回路電流方程寫為

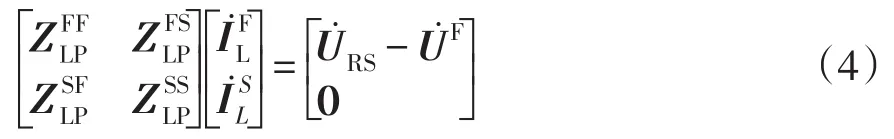
消去第2類回路對應各行，回路方程變為

方程（10）消去了第2類回路對應的方程，方程個數為第1類回路個數，即負荷節點及分布式電源節點的總數。這樣處理的優點在于，雖然第2類回路的出現會使回路方程數量增多，但在進一步建立潮流方程之前將其等值，使回路方程規模與第2類回路出現前相同，不會增加潮流計算的計算量。

另一方面，由兩類回路的定義可見，即使合環支路為小阻抗或零阻抗支路，因其不在第1類回路中，也不會是第1、2類回路之間的互阻抗，不會對第1類回路產生影響；而第2類回路自阻抗則至少含有兩個正常阻抗支路，也不會出現過小的情況。

2　基于回路方程的配電網潮流計算

2.1基于回路分析的潮流方程

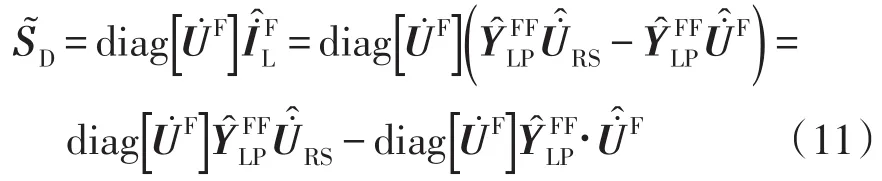
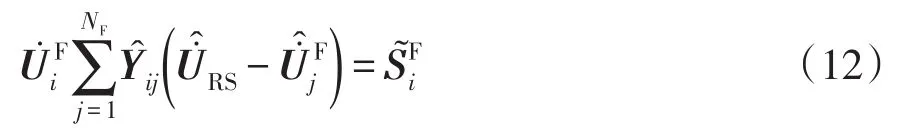
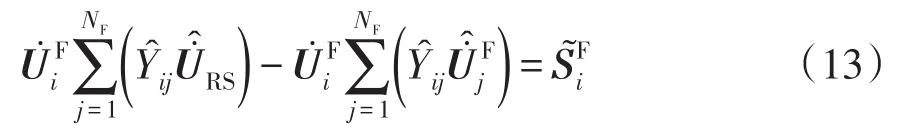
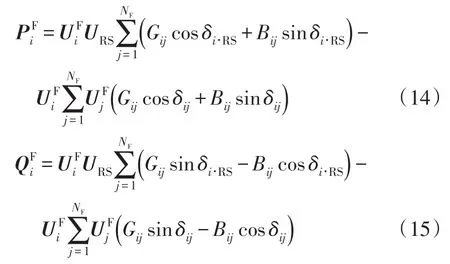
式中：δi·RS為節點i電壓相量與根節點電壓相量的相角差；δij節點i、j電壓相量的相角差。節點注入功率不平衡量為

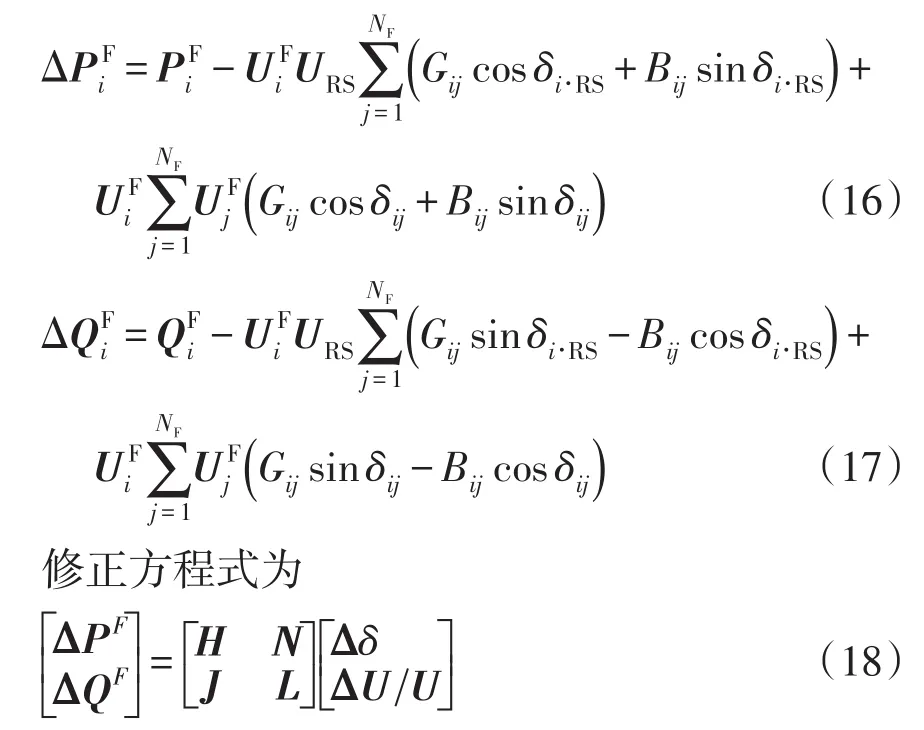
4個子矩陣H、N、J、L構成了修正方程式的雅可比矩陣。當i≠j時，雅可比矩陣的各個元素分別為

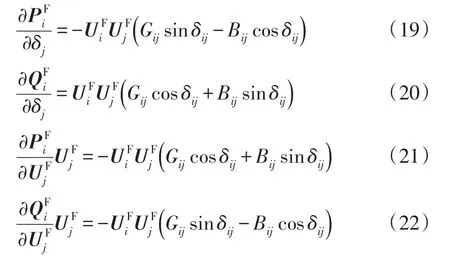
δj為節點 j電壓相量與參考節點電壓相量的相角差。當i=j時，雅可比矩陣的各個元素分別為

2.2牛頓法潮流計算步驟

在建立式（14）、（15）形式的潮流方程后，采用牛頓法求解，求解過程與采用牛頓法求解節點形式潮流方程基本相同，其步驟簡述如下。

（1）讀取系統原始數據，形成支路阻抗矩陣，根據回路與支路阻抗矩陣的關系，求取回路阻抗的矩陣；

（2）根據式（6）～（8）消去第2類回路，求出等效回路導納矩陣；

（4）將各節點電壓的初值代入式（16）、（17）求出功率不平衡量

（5）將各節點電壓的初值代入式（19）～（26），求出雅可比矩陣的各個元素

由1.1小節建立回路方程的分析可知，潮流計算收斂后可直接得到負荷節點電壓列向量和第1類回路的回路電流列向量；由1.3節式（4）可得第2類回路的回路電流列向量為

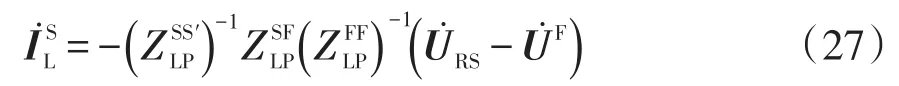
3　線性方程組系數矩陣的條件數

無論采用節點方程形式，還是采用回路方程形式，牛頓法中求解的修正方程都是一個以潮流方程雅可比矩陣為系數矩陣的線性方程組。

對于線性方程組的系數矩陣A，其條件數為

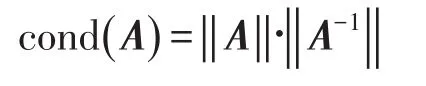
‖·‖為某種矩陣范數，如2-范數。由矩陣分析理論可知，系數矩陣的條件數可反映矩陣的非奇異程度。條件數越小，矩陣A的非奇異程度越高；條件數越大，A的非奇異程度越差，呈現“病態”。

對含小阻抗支路的電網絡建立節點導納矩陣并據此建立潮流方程，采用牛頓法求解，其迭代過程中的雅可比矩陣條件數非常大，矩陣為病態。數值計算時處理病態線性方程組的方法或是對系數矩陣進行預處理［12-14］，如文獻［12］；或是采用更高的計算精度，如文獻［10］所指出的那樣。

對于同一電網絡，根據2.2小節回路導納矩陣建立的潮流方程，采用牛頓法求解，迭代過程中的雅可比矩陣條件數要小得多，非奇異程度高，對應的線性方程組收斂性好。因此，不必采用提高計算精度或對雅可比矩陣進行預處理等特殊方法處理小阻抗支路帶來的收斂性問題。

在下文第4.1小節中，分別計算了節點形式和回路形式兩種潮流方程迭代過程中雅可比矩陣的條件數，用來反映潮流方程的病態程度。

4　算例分析

基于Matlab R2010a實現下文所用各方法，各算法都采用雙精度數據類型，允許誤差設為1×10-6。采用本文回路形式潮流牛頓法對IEEE33節點系統［8］、PG&E69節點系統［15］及文獻［7］的90節點系統進行計算，計算均能可靠準確收斂，表明了本文算法的正確性。下面分別從迭代次數、雅可比矩陣的條件數、處理環網能力及處理PV節點幾個方面進行分析。

4.1迭代次數

表1中對比了本文算法（算法1）與直接法（算法2）、電流前推回代法（算法3）、傳統節點形式潮流方程牛頓法（算法4）迭代次數。

表1　4種算法潮流迭代次數比較Tab.1　Comparison of the number of iterations among four kinds of algorithms

由表1可見，對于文獻［7］的90節點系統，傳統牛頓法由于受到小阻抗支路的影響不收斂；本文算法通過建立回路方程，避免了求取節點導納矩陣，取而代之的是回路導納矩陣，算法收斂。從表中還可看出，對于含有PV節點的網絡以及弱環網，本文算法收斂所需迭代次數與算法4收斂時相同，明顯少于算法2與算法3。

4.2雅可比矩陣條件數

采用牛頓法求解文獻［7］的90節點系統的節點形式潮流方程不收斂，而牛頓求解本文回路形式潮流方程則是收斂的。表2給出了兩種算法下前五次迭代過程雅可比矩陣的條件數。由表2可見，前者迭代過程中的雅可比矩陣條件數很大，非奇異程度很差，相應線性方程組呈現病態，因此迭代不收斂；而后者雅可比矩陣條件數相對很小，非奇異程度較好，迭代5次后收斂。

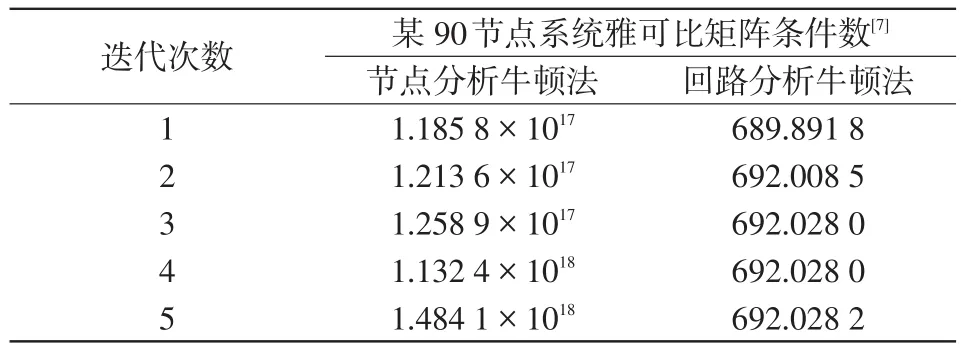
表2　兩種算法關于雅可比矩陣條件數的比較Tab.2　Comparison of Jacobian condition number between two algorithms

4.3環網數對收斂性的影響

表3是在IEEE33節點系統加入了合環支路，考察本文算法處理環網的能力。可見，隨著環網個數的增多，迭代次數并無明顯變化；算例表明本文算法具有較強的環網處理能力，計算弱環網潮流時穩定性更高，收斂效果更好。

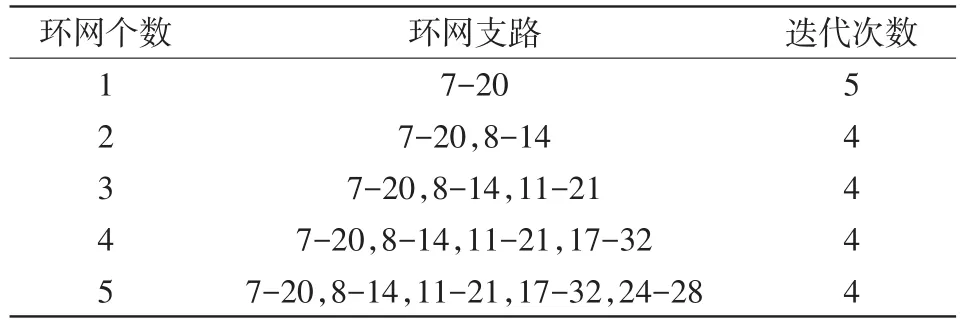
表3　環網個數對IEEE33節點系統收斂影響Tab.3　Impact of the number of meshes on convergence of IEEE 33-node system

4.4PV節點數對收斂性的影響

表4反映了采用本文模型與方法計算IEEE33節點系統含有分布式電源節點為PV節點的情況。可見，迭代次數并未隨著PV節點接入個數的增多而增多。算法把根節點作為平衡節點，其他分布式電源作為PV節點。牛頓法處理PV節點的高效特性是直接阻抗法和前推回代法等支路法無法達到的。

表4　PV節點個數對IEEE33節點系統收斂影響Tab.4　Impact of the number of PV nodes on convergence of IEEE 33-node system

5　結論

本文建立了基于回路形式配電網潮流方程，并采用牛頓法進行求解。與傳統方法相比，除了可以用于含分布式電源這一特點外，本文方法還具有以下特點：

（1）采用回路分析，能高效處理弱環配電網的潮流計算問題，不需在迭代計算中采用補償方法計算環路電流，方程數即為負荷及電源節點數，環路支路不影響方程組規模，也不會增加求解過程的計算量；

（2）采用牛頓法求解潮流方程，對PV節點的處理過程和能力與牛頓法求解輸電網潮流的情況相同，因此，本文方法可直接用于求解含有分布式電源的配電網潮流計算；

（3）本文方法基于回路分析及回路矩陣，在網絡中含有小阻抗支路時，迭代過程中的雅可比矩陣條件數較小，非奇異程度高，避免了采用節點分析與節點矩陣時“病態”雅可比矩陣的出現，收斂性較好。在基于節點導納矩陣的潮流計算因小阻抗支路存在不易收斂的情形下，本文模型與算法是獲得配電網潮流分布一個有效的替代解決方案。

回路導納矩陣是一個滿陣，而節點導納矩陣則是一個稀疏矩陣。因此，基于相同規模的回路導納矩陣和節點導納矩陣的潮流計算迭代過程，前者的計算量要高于后者，這是回路方法的一個不足。但是，由于配電網的回路數要小于節點數，其回路導納矩陣的規模也要小于節點導納矩陣，這在一定程度上抵消了因回路導納矩陣為滿陣而帶來的計算量的增大。

［1］王成山，李琰，彭克（Wang Chengshan，Li Yan，Peng Ke）.分布式電源并網逆變器典型控制方法綜述（Overview of typical control methods for grid-connected inverters of distributed generation）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2012，24（2）：12-20.

［2］王進，劉嬌，陳加飛，等（Wang Jin，Liu Jiao，Chen Jiafei，et al）.計及風電不確定性的配電網無功模糊優化（Research on reactive power fuzzy optimization of distribution network with wind turbines）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2015，27（6）：8-13.

［3］王建勛，呂群芳，劉會金，等（Wang Jianxun，Lyu Qunfang，Liu Huijin，et al）.含分布式電源的配電網潮流快速直接算法（Fast and direct power flow algorithm for distribution network with distributed generation）［J］.電力自動化設備（Electric Power Automation Equipment），2011，31（2）：17-21.

［4］付英杰，汪沨，陳春，等（Fu Yingjie，Wang Feng，Chen Chun，et al）.考慮分布式電源的配電網電壓控制新方法（New method of voltage control considering distribution network containing distributed generation）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2015，27（6）：26-31.

［5］朱星陽，張建華，劉文霞，等（Zhu Xingyang，Zhang Jianhua，Liu Wenxia，et al）.考慮負荷電壓靜特性的含分布式電源的配電網潮流計算（Power flow calculation of distribution system with distributed generation considering static load characteristics）［J］.電網技術（Power System Technology），2012，36（2）：217-223.

［6］丁明，郭學鳳（Ding Ming，Guo Xuefeng）.含多種分布式電源的弱環配電網三相潮流計算（Three-phase power flow for the weakly meshed distribution network with the distributed generation）［J］.中國電機工程學報（Proceedings of the CSEE），2009，29（13）：35-40.

［7］Chang Gary，Chu Shou-Yung，Hsu Ming-Fong，et al.An efficient power flow algorithm for weakly meshed distribution systems［J］.Electric Power Systems Research，2012，84（1）：90-99.

［8］車仁飛，李仁俊（Che Renfei，Li Renjun）.一種少環配電網三相潮流計算新方法（A new three-phase power flow method for weakly meshed distribution systems）［J］.中國電機工程學報（Proceedings of the CSEE），2003，23（1）：74-79.

［9］Goswami S K，Basu S K.Direct solution of distribution systems［J］.IEEE Proceedings C，1991，138（1）：78-88.

［10］Tylavsky D J，Crouch P E，Jarriel L F，et al.The effects of precision and small impedance branches on power flow robustness［J］.IEEE Trans on Power Systems，1994，9（1）：6-14.

［11］姚玉斌，魯寶春，陳學允（Yao Yubin，Lu Baochun，Chen Xueyun）.小阻抗支路對牛頓法潮流的影響及其處理方法（A method to deal with the effect of small impedance branches to prevent divergence inNewton-Raphson load flow）［J］.電網技術（Power System Technology），1999，23（9）：27-31.

［12］胡博（Hu Bo）.大規模復雜電力系統并行潮流計算和并行可靠性跟蹤研究（Parallel Algorithms of Power Flow and Unreliability Tracing for Large-Scale Complex Power Systems）［D］.重慶：重慶大學電氣工程學院（Chongqing：School of Electrical Engineering of Chongqing University），2010.

［13］薛毅.數值分析與科學計算［M］.北京：科學出版社，2011.

［14］周碩，郭麗杰，吳柏生（Zhou Shuo，Guo Lijie，Wu Baisheng）.Jacobi迭代預處理中的條件數與迭代次數的關系（Relation between condition number and iteration degrees in Jacobi iteration pretreatment）［J］.東北電力學院學報（Journal of Northeast China Institute of Electric Power Engineering），2003，23（6）：57-60.

［15］王守相，王成山.現代配電系統分析［M］.北京：高等教育出版社，2007.

Newton Method for Solving Power Flow of Distribution Networks with Small Impedance Branches

CHU Zhuang1，YU Qunying2，LI Xiaowei3
（1.College of Electrical Engineering，Northeast Dianli University，Jilin 132012，China；2.Electric Power Research Institute，State Grid Jilin Electric Power Ltd，Changchun 130000，China；3.Jilin Province Transmission and Substation Engineering Company，Changchun 130000，China）

The non-convergence of Newton method for the power flow computation of distribution networks is mainly due to the ill condition of Jacobi matrix built on node admittance matrix.In this paper，two kinds of loops are defined by two kinds of links respectively，i.e.，equivalent branches of loads and branches for closing.The model of power flow is based on loop-current load-node-voltage equations，and the parameters of small impedance branches are not independent elements in the network matrix.Newton method is applied to solving the equations，and the Jacobi matrix based on loop-admittance matrix is well-conditioned，which ensures the convergence of computation.Different cases with branches for closing and PV nodes indicate the correctness and efficiency of the proposed method.

power flow computation of distribution networks；convergence；loop analysis；Newton method；small impedance branches

TM712

A

1003-8930（2016）09-0036-06

10.3969/j.issn.1003-8930.2016.09.006

初壯（1973—），男，博士，副教授，研究方向為電力系統運行分析。Email：chuzhuang@hotmail.com

于群英（1988—），男，碩士，助理工程師，研究方向為電力系統運行分析。Email：happy7998523@126.com

李笑薇（1988—），女，本科，助理工程師，研究方向為電力系統運行分析。Email：happy6181056@126.com

2014-09-25；

2015-11-30

國家高技術研究發展計劃（863計劃）資助項目（2014AA052502）