基于秦嶺樣區的四種時序EVI函數擬合方法對比研究

劉亞南，肖　飛，杜　耘

1 中國科學院測量與地球物理研究所，武漢　430077 2 湖北省環境與災害監測評估重點實驗室，武漢　430077 3 中國科學院大學，北京　100049

?

基于秦嶺樣區的四種時序EVI函數擬合方法對比研究

劉亞南1,2,3，肖飛1,2,*，杜耘1,2

1 中國科學院測量與地球物理研究所，武漢430077 2 湖北省環境與災害監測評估重點實驗室，武漢430077 3 中國科學院大學，北京100049

函數曲線擬合方法是植被指數時間序列重建的一個重要方法，已經廣泛應用于森林面積動態變化監測、農作物估產、遙感物候信息提取、生態系統碳循環研究等領域。基于秦嶺樣區多年MODIS EVI遙感數據及其質量控制數據，探討并改進了時序EVI重建過程中噪聲點優化和對原始高質量數據保真能力的評價方法；在此基礎上，比較了常用的非對稱性高斯函數擬合法(AG)、雙Logistic函數擬合法(DL)和單Logistic函數擬合法(SL)。基于SL方法，調整了模型形式并重新定義d的參數意義，提出了最值優化單Logistic函數擬合法(MSL)，并與其他3種方法進行對比。結果表明；在噪聲點優化及保留原始高質量數據方面，AG方法和DL方法二者整體差別不大，而在部分像元的處理上AG方法表現出更好的擬合效果；MSL方法和SL方法相比于AG方法和DL方法其效果更為突出；在地形氣候復雜，植被指數噪聲較多的山區，MSL方法表現出更好的適用性。

MODIS EVI；曲線擬合；時間序列重建；Logistic；秦嶺

植被指數數據已經廣泛應用于農情監測、物候信息提取、碳通量估算、陸地生態系統對氣候變化的響應等研究領域[1- 3]。然而，遙感獲取的植被指數時間序列曲線包含很多噪聲點，往往對研究精度造成很大影響[4- 5]。為有效濾除噪聲，學者發展了一系列植被指數時間序列重建方法。主要包括：NDVI閾值法[6- 7]、后向移動平均法[8]、最大上升速率判斷方法[9]、曲線擬合法[10]和經驗回歸方程法[11]，動態權重濾波法[12]。其中，函數曲線擬合法針對每一像元進行單獨處理，利用函數方程對植被指數時間序列曲線進行重建，不需設定閾值或經驗系數，故在不同環境條件中得到廣泛應用[13- 16]。有學者研究發現函數曲線擬合方法總體上優于濾波方法[17- 18]。

函數曲線擬合最常用的方法包括：非對稱性高斯函數擬合法(AG)、雙Logistic函數擬合法(DL)和單Logistic函數擬合法(SL)。Jonsson等利用非對稱高斯函數擬合法對西非地區時序NDVI數據進行重建，發現其效果要優于濾波方法[17]。雙 Logistic 函數擬合法(DL)對于生長季較短的高緯度地區具有很好的適用性，但是對中緯度地區的植被指數的重建效果需要進一步驗證[15]。單Logistic函數擬合方法針對各個生長季的不同特點分段擬合，對于生長季較長或年內具有多個生長季的地區也能適用[10]。

不同函數曲線擬合方法對不同地理環境有不同的適應性。尤其山地區域，因其地形復雜、數據噪聲大，不同函數曲線擬合方法往往結果差異較大。因而，在區域研究中，通常需要對比選擇一種適用于區域植被指數波動特征的曲線擬合方法。

目前，擬合方法的對比研究大多從直觀視覺角度出發來判別噪聲點及其擬合重建效果。傳統的求算擬合相關系數和回歸估計標準差(RMSE)的方法，只能表現對原始數據的擬合程度，無法定量表征噪聲點的影響程度，因而也無法充分說明重建后的曲線保留原始高質量數據的能力[18- 21]。

本文基于秦嶺樣區MODIS EVI多年遙感數據及其質量評價數據，探討并發展了時序NDVI重建過程中噪聲點優化和原始高質量數據保真能力的評價方法；對比了常用的 AG方法、DL方法和SL方法的擬合效果，并將上述三種方法和我們基于山區植被指數波動特征改進的MSL方法做了比較研究。

1　研究區及數據

本文選取了均勻分布于秦嶺的10個樣區進行分析。秦嶺為濕潤地區和半濕潤地區的分界線、地形起伏較大、植被時空分異明顯，以其作為樣區具有較好典型性和代表性。樣區位置如圖1所示。

研究使用的實例數據選擇EOS/Terra衛星的MODIS MOD13Q1產品，其中包括基于MVC方法16d合成的250m分辨率EVI及其質量控制數據。與EVI相比，NDVI 在植被生長旺盛期容易達到飽和[20]，EVI比NDVI的動態變幅更大[21]，能更真實地反映植被的生長變化過程。數據來源于中國科學院計算機網絡信息中心地理空間數據云(http://www.gscloud.cn)。該產品經過幾何校正和大氣校正。EVI值的標準范圍為-1.0—1.0。MOD13Q1 EVI產品是-3000—10000的DN值，-3000為填充值，從DN值轉化成 EVI 值的關系式為:

NDVI=0.0001·DN

(1)

秦嶺樣區是利用MOD13Q1的兩景圖像通過MRT拼接裁剪和投影變換得到。此外，還需從MOD13Q1的兩景EVI產品中提取 data pixel reliability數據集，其空間、時間分辨率與EVI數據集匹配。該數據對區域每個像元EVI數據質量進行說明，分為5個不同等級，其中DN值等級為0的數據質量最高。本研究中將DN值等級為0和1的符合質量要求的像元作為擬合的原始數據，其他則全部設為NAN不參與計算。所以可能出現某些期EVI數據是空值的情況。樣區2011—2013的原始EVI數據，共8328個像元(2776×3年)。

圖1　秦嶺樣區位置分布圖Fig.1　Distribution of the sample sites in the Qinling Mountains

2　4種函數曲線擬合方法

2.1常用函數曲線擬合方法介紹

非對稱性高斯函數擬合法(AG)、雙Logistic函數擬合法(DL)和單Logistic函數擬合法(SL)是目前最常用的函數曲線擬合方法。

非對稱高斯函數擬合方法(AG)是一個從局部擬合到整體擬合的方法過程, 使用分段高斯函數來模擬植被生長過程, 最后通過平滑連接各高斯擬合曲線實現時間序列重建[17]。其過程大致可分為3 步驟：區間提取、局部擬合和整體連接[20]。

Pieter S.A.等，于2006年研究高緯度地區植被物候提取問題提出雙Logistic曲線擬合法[13]。首先，將整個時間序列中時間點對應的值按極大或極小值分成多個區間, 分別對該區間進行雙 Logistic 函數局部擬合，最后再和AG一樣，進行整體連接。

張曉陽[10]等提出了利用單Logistic函數擬合方法。單Logistic函數是一種分段式Logistic函數擬合的方法，利用擬合曲線曲率變化的特點，確定EVI時序曲線上植物各物候轉換期。具體形式為：

(2)

式中，y(t)是t時刻的EVI值，a、b為擬合參數，d為植被指數初始背景值，c+d為最大值。此方法針對各個生長季的不同特點分段擬合，對于生長季較長或年內具有多個生長季的地區也能適用，而且有十分廣泛的應用[13-14,22-23]。Logistic模型方法同時被NASA(National Aeronautics and Space Administration)作為計算其MODIS全球物候數據產品MGLCD(MODIS Global Land Cover Dynamics Product)的方法之一。

2.2最值優化單Logistic函數擬合法(MSL)

原單Logistic模型中，參數d作為植被指數初始背景值，其通常通過植被指數時間數據序列直接計算得出，一般為植被指數時間序列中的最小值[21]。然而，由于植被指數最小值處于植被休眠期內(生長季初始或生長季末期)，此時地表植被覆蓋度很低，地表下墊面背景對數據干擾較大，其時空變化往往導致植被指數最小值產生較大波動，這是導致模型擬合精度降低的原因之一。在分析了秦嶺地區多年EVI最值波動特征的基礎上，本文發現其最大值相對其最小值更為穩定。

基于上面的原因，本文對模型形式進行改動，并重新定義d的參數意義。

(3)

式中,d為最大EVI值；a、b、c是待擬合參數，其意義同前。由于EVI數據序列最大值相對較為穩定，使得上述改進的模型形式希望能達到較好的擬合效果。

3　基于秦嶺樣區4種方法的擬合效果對比分析

3.1時序植被指數擬合效果評價方法探討

對呈鋸齒狀波動的植被指數平滑重建是為了最大程度消除噪聲點的影響，同時保留高質量原始數據，還原植被生長的季節性變化特征。然而不同的重建方法差別很大，如何客觀定量的比較不同方法的優劣是十分重要的問題。上包絡線分析法、擬合曲線特征直觀比較法、擬合指標評價法和相關統計量分析法是目前常用的幾種評價方法。在實際研究中往往需要幾種方法綜合使用，如Jonsson等參考原始時序NDVI數據上包絡線，同時比較不同擬合曲線形態特征得出AG方法總體上要優于兩種濾波方法[17]。上包絡線分析法及擬合曲線特征直觀比較法往往從直觀的視覺角度出發來衡量不同擬合方法對噪聲點的擬合重建效果，主觀干擾較強，因而有些學者輔助其他方法來進行定量分析。如宋春橋等除了比較擬合曲線和原始數據的上包絡線之外，還利用擬合的相關系數和回歸估計標準差對AG方法、DL方法和Savitzky-Golay濾波方法進行了比較研究[18]。曹云鋒等引入NDVI均值、NDVI平均絕對誤差和相對誤差等統計量來比較分析3種濾波算法[21]。朱文泉等，基于模擬的真實的EVI時序曲線再混進不同程度的噪聲來評價不同擬合方法抗噪聲干擾的能力[12]。

通過比較原始數據上包絡線和不同擬合曲線的特征，能夠準確判斷不同擬合曲線對原始數據的擬合重建效果，對噪聲點的敏感性及其優化噪聲點的能力。然而，這種比較只局限于個別像元的對比，缺乏客觀的定量指標來衡量不同擬合方法對整個研究區域所有像元的擬合能力；同時此方法對噪聲點的正確判讀依賴很大，容易受到研究者主觀因素的影響，將個別突降的低值判定為噪聲點，卻忽略了連續噪聲點的情況。有些學者選用了相關系數和回歸估計標準差(RMSE)等指標來對不同曲線擬合效果進行定量分析[14],相關系數表明兩組數據之間的相關強度；而RMSE可以表明兩組數據之間平均差異程度。相對于NDVI均值、NDVI平均絕對誤差和相對誤差等統計量，相關系數和RMSE能更好的衡量不同擬合曲線的擬合效果。通過對不同方法擬合區域每個像元得到的相關系數和RMSE再分別求取均值，或者進行差值比較，可以從整體上評價不同方法對研究區的適用性。然而，如果只簡單將擬合前后的數據進行組合，求算得到的相關系數和RMSE則不能突出擬合后的數據與高質量原始數據之間的相關程度，無法充分說明重建后的曲線保留原始高質量數據的能力。

本文利用質量控制數據定位噪聲點(質量級別為1)，而不是主觀判定突降的低值為噪聲點，能相對客觀的比較不同擬合曲線對噪聲的重建效果。在此基礎上，用去除噪聲點的高質量原始數據(質量級別為最高0)和與其相對應的擬合重建后的EVI數據進行組合求算相關系數和回歸估計標準差(RMSE)，因而求算出的相關系數和RMSE能夠充分說明重建后的曲線與原始高質量數據的相關性及差異性。

3.24種方法擬合效果的直觀比較

基于上述方法，本文從秦嶺10個樣區中抽取4種方法擬合效果差別較大的6個典型像元對EVI時間序列重建前后的曲線進行對比分析(圖2)。

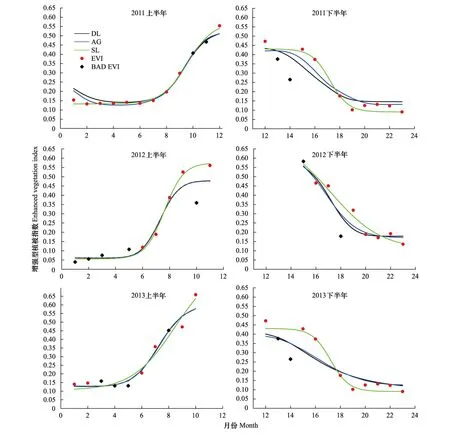
圖2　2011—2013年6個生長季的典型像元EVI(Enhanced Vegetation Index) 時間序列重建前后曲線對比Fig.2　Comparison of the original and reconstructed MODIS EVI time-series during 2011—2013

TIME表示影像期號，MOD13Q1數據是16d合成，一年23期。圖2中可以看出，4種法都不同程度的去除了鋸齒波動，重建后的EVI曲線更加平滑。4種方法都會受到連續噪聲點(質量級別為1的BAD EVI)的影響，如2012上半年的1、2、3、5期和2013上半年年的3、4、5期。

總體上，AG方法和DL方法的擬合曲線比較接近，但都對噪聲點比較敏感，曲線形態容易受到噪聲點的影響發生變化。這種影響大多發生在生長季的初期和末期。但是在生長季的中期也會受到影響。如2012下半年的第18(9月份)期和2013上半年的第14期(7月份)。MSL方法和SL方法的擬合曲線有較好的一致性；相比于AG方法和DL方法，MSL方法和SL方法對高質量EVI原始數據(質量級別為0的 EVI數據)有更好的重建效果。

3.34種方法擬合效果的定量分析

本文利用4種方法擬合3年6個生長季EVI數據(6×2776個像元)，并用去除噪聲點的高質量原始數據(質量級別為最高0)和與其相對應的擬合重建后的數據進行組合求算相關系數和RMSE，對比其各生長季的整體平均值，以此反映4種方法對不同生長季EVI 重建保真性能力(表1,表2)。

表1和表2中可以看出，MSL方法擬合的相關系數各期都高于其他3種方法，MSL方法擬合的RMSE都各期要小于其他3種方法，其中2011年上半年和2012年，這種效果比較明顯，反映出MSL方法保留高質量原始數據的能力更強。同時說明MSL方法擬合值與原始值之間的平均差異程度更小，代表性更好。SL方法的表現比MSL方法稍差，但是優于AG方法和DL方法。除了在2011和2012上半年，AG方法與DL方法差別不是很大。

表1　4種方法擬合2011—2013年EVI數據的相關系數的總體均值

非對稱性高斯函數擬合法(AG)、雙Logistic函數擬合法(DL)和單Logistic函數擬合法(SL)

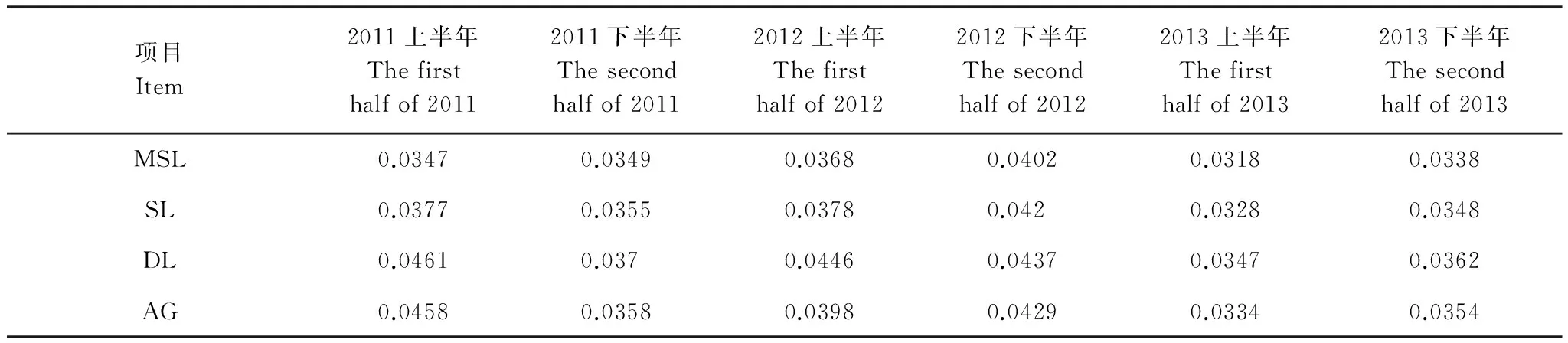
表2　4種方法擬合2011—2013年EVI數據的RMSE的總體均值

本文統計了4種方法擬合相關系數差值大于0的像元點個數占該生長季總像元數(2776)的比例(圖3)。

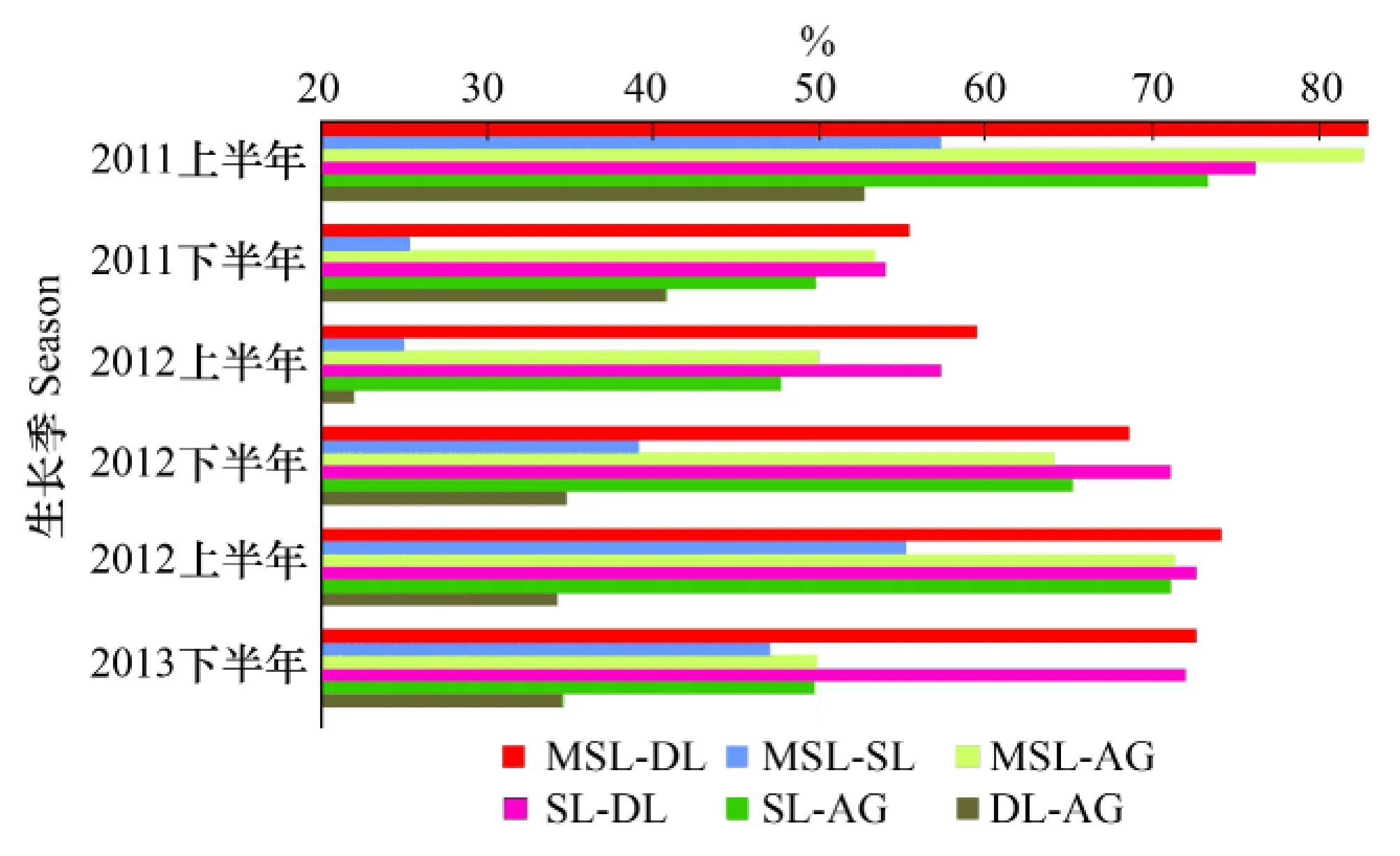
圖3　4方法擬合的相關系數差值大于0的像元的百分比　Fig.3　The percentage of pixels which correlation coefficient difference greater than zero among the four methods

從圖3可以看出，MSL與SL相比，在2011年上半年和2013上半年，相關系數差值大于0的像元占該期總像元數的比例都大于50%；MSL方法與AG方法和DL方法相比，相關系數差值大于0的像元占該期總像元數的比例都不小于50%，其中2011年上半年和2013年達到70%以上。SL方法與DL方法的相關系數差值大于0的像元占該期總像元數的比例都大于50%；SL與AG方法的比較中，2011上半年，2012下半年和2013上半年，這種比例都超過60%。綜上所述，相對于其他3種方法，MSL方法在對絕大多數像元的擬合上，都表現出更好的效果。MSL方法和SL方法比另外兩種方法保留高質量原始數據的能力更強。

經分析3年6個生長季的EVI實驗數據(6×2776個像元)發現，噪聲點數目小于3個的象元比例為17%，小于等于4個的為82%，為了進一步分析4種方法對不同程度噪聲的抗干擾能力，本文分別隨機從實驗數據中提取噪聲點數目小于3個，3—4個和大于4個的像元各500個。利用4種方法分別擬合這3種EVI數據得到RMSE，并對比分析其均值(表3)。

從表3可以看出，MSL和SL比DL和AG抗噪聲干擾的能力更強。對包含較多噪聲的像元的擬合，MSL比SL、DL和AG表現出更好的擬合效果，RMSE總體均值明顯低于其它3種方法。MSL擬合方法抗噪聲干擾的能力最強。

表3　4種方法擬合EVI數據的RMSE均值

3.4分析與討論

函數曲線擬合法針對每一像元進行單獨處理，利用函數方程對植被指數時間序列曲線進行重建，不需設定閾值或經驗系數。而其他方法，如NDVI閾值法、后向移動平均法、最大上升速率判斷方法都需要先設定一個合理的閾值或經驗系數。地形復雜的山區往往缺乏足夠的物候觀測數據來確定閾值或經驗系數，故本文重點對比分析了常用的函數曲線擬合方法。然而，函數擬合方法會受其限定的函數曲線形態的影響，與其他方法相比，也表現出一定的局限性。如在人為干預較大的農耕地區，植被指數曲線往往呈現多鋒，動態濾波方法則能達到更好的效果。Logistic函數曲線的特點是開始增長緩慢，而在以后的某一范圍內迅速增長，達到某限度后，增長又緩慢下來。曲線略呈拉長的“S”型。這種特點符合絕大多數自然植被的生長規律，在函數曲線擬合方法中最為常用。AG和DL模型都是以整個生長季為擬合區間的(往往為1a)，其曲線形態近似為“幾“字形。其優點在于，在缺乏有效觀測數據的情況下，也能大致模擬出植被整個生長季的生長特征。在生長季較短的高緯度地區，一年內植被長時間處于休眠期，植被生長期非常短，植被指數的振幅很小，加上雪蓋云掩等影響，往往缺乏有效觀測數據來分段模擬植被生長期或者衰老期的變化特征。在這種情況下，與MSL和SL相比，AG和DL就有一定優勢。一年中，各個生長季EVI波動特征有不同特點，很多象元上下半年的EVI曲線呈現非對稱性。分段擬合能較合理的還原植被生長的季節性變化特征，而且有更大的靈活性。在地形氣候復雜的中緯度山區，植被上下半年的自然生長規律都呈現出較好的“S”型曲線形態，與AG和DL相比，SL和MSL的擬合效果更佳。與其他3種函數曲線擬合方法相比，MSL擬合方法有更強的抗噪聲干擾的能力。

本文所采用的幾種函數曲線擬合方法都屬于最小二乘非線性擬合方法，非線性回歸過程可以獲得模型參數的最小二乘無偏性估計。所采用的算法分為3種：Trust-Region算法、Gauss-Newton算法、和Levenberg-Marquardt算法。利用這此算法進行迭代時,都必須先給出模型中各參數的初始值。初始值選擇不當會對擬合結果造成很大影響。本文選用的是最為常用的Levenberg-Marquardt算法，它是利用梯度求最值的算法，屬于“爬山”法的一種，同時具有Trust-Region算法和Gauss-Newton算法的優點。在參數初始值的確定上，本文先基于模型參數的生態學意義限定某參數的取值范圍并利用三點法進行估算(如logistic函數中，c為環境負載力或容納量，其值大于0)，然后利用線性化回歸求出模型其他參數的估計值并且進行顯著性檢驗，再以此估計值為初始值進行非線性回歸。這樣可以最少的迭代次數獲得參數滿意的擬合精度。還有很多可以對參數初始值進行估算的方法，如四點法、拐點法、遺傳算法等。有關非線性函數曲線擬合參數初始值的估算目前還沒有一種公認的最優算法。

4　結論

本文基于質量控制數據，改進了時序EVI數據重建效果的定量評價方法，能相對客觀的比較不同擬合曲線對噪聲點的重建效果及其保持原始高質量數據的能力。基于改進的評價方法，本文以秦嶺均勻分布的10個樣區為研究區，對比了非對稱性高斯函數擬合法(AG)、雙Logistic函數擬合法(DL)、單Logistic函數擬合法(SL)和最值優化單Logistic函數擬合法(MSL)，結果表明：與AG和DL相比，MSL和SL在噪聲點優化和保留原始高質量數據的能力方面更為突出，同時擬合值與原始值之間的平均差異程度更小，代表性更好。AG和DL的擬合曲線比較接近，但都對噪聲數據比較敏感，曲線形態容易受到噪聲點的影響發生變化。AG相對于DL，在部分像元的處理上擬合效果更好。MSL比SL、DL和AG表現出更好的擬合效果，在噪聲點較多的情況下這種效果更為突出。4種方法擬合效果的優劣依次是MSL>SL>AG>DL。

[1]李正國, 楊鵬, 周清波, 王仰麟, 吳文斌, 張莉, 張小飛. 基于時序植被指數的華北地區作物物候期/種植制度的時空格局特征. 生態學報, 2009, 29(11): 6216- 6226.

[2]何月, 樊高峰, 張小偉, 柳苗, 高大偉. 浙江省植被NDVI動態及其對氣候的響應. 生態學報, 2012, 32(14): 4352- 4362.

[3]Zhu W Q, Chen G S, Jiang N, Liu J H, Mou M J. Estimating carbon flux phenology with satellite-derived land surface phenology and climate drivers for different biomes: A synthesis of AmeriFlux observations. Plos One, 2013, 8(12): e84990.

[4]Josef Cihlar, Hung Ly, Li Z Q, Chen J, Hartley Pokrant, Huang F T. Multitemporal, multichannel AVHRR data sets for land biosphere studies——artifacts and corrections. Remote Sensing of Environment, 1997, 60(1): 35- 57.

[5]李杭燕, 頡耀文, 馬明國. 時序NDVI數據集重建方法評價與實例研究. 遙感技術與應用, 2009, 24(5): 596- 602.

[6]Daniel Lloyd. A phenological classification of terrestrial vegetation cover using shortwave vegetation index imagery. International Journal of Remote Sensing, 1990, 11(12): 2269- 2279.

[7]Michael A White, Peter E Thornton, Steven W Running. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Global Biogeochemical Cycles, 1997, 11(2): 217- 234.

[8]Bradley C Reed, Jesslyn F Brown, Darrel VanderZee, Thomas R Loveland, James W Merchant, Donald O Ohlen. Measuring Phenological Variability from Satellite Imagery. Journal of Vegetation Science, 1994, 5(5): 703- 714.

[9]J?rg D Kaduk, Martin Heimann. A prognostic phenology scheme for global terrestrial carbon cycle models. Climate Research, 1996, 6(1): 1- 19.

[10]Zhang X Y, Mark A Friedl, Crystal B Schaaf, Alan H Strahler, John C F Hodges, Gao F, Bradley C Reed, Alfredo Huete. Monitoring vegetation phenology using MODIS. Remote Sensing of Environment, 2003, 84(3): 471- 475.

[11]Zhu W Q, Pan Y Z, He H, Wang L L, Mou M J, Liu J H. A changing-weight filter method for reconstructing a high-quality NDVI time series to preserve the integrity of vegetation phenology. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(4): 1085- 1094.

[12]Moulin S, Kergoat L, Viovy N, Dedieu G. Global-scale assessment of vegetation phenology using NOAA/AVHRR satellite measurements. Journal of Climate, 1997, 10(6): 1154- 1170.

[13]Pieter S A Beck, Clement Atzberger, Kjell Arild H?gda, Bernt Johansen, Andrew K Skidmore. Improved monitoring of vegetation dynamics at very high latitudes: a new method using MODIS NDVI. Remote Sensing of Environment, 2005, 100(3): 321- 334.

[14]吳文斌, 楊鵬, 唐華俊, 周清波, Shibasaki Ryosuke, 張莉, 唐鵬欽. 過去20年中國耕地生長季起始期的時空變化. 生態學報, 2009, 29(4): 1777- 1786.

[15]苗翠翠, 江南, 彭世揆, 呂恒, 李揚, 張瑜, 王妮, 李軍. 基于NDVI時序數據的水稻種植面積遙感監測分析——以江蘇省為例. 地球信息科學學報, 2011, 13(2): 273- 280.

[16]Aziz Habib, Chen X L, Gong J Y, Wang H Y, Zhang L. Analysis of China vegetation dynamics using NOAA-AVHRR data from 1982 to 2001. Geo-spatial Information Science, 2009, 12(2): 146- 153.

[17]Jonsson P, Eklundh L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40: 1824- 1832.

[18]宋春橋, 游松財, 柯靈紅, 劉高煥. 藏北地區三種時序NDVI重建方法與應用分析. 地球信息科學學報, 2011, 13(1): 133- 143.

[19]Jennifer N Hird, Gregory J McDermid. Noise reduction of NDVI time series: an empirical comparison of selected techniques. Remote Sensing of Environment, 2009, 113(1): 248- 258.

[20]李儒, 張霞, 劉波, 張兵. 遙感時間序列數據濾波重建算法發展綜述. 遙感學報, 2009, 13(2): 335- 341.

[21]曹云鋒, 王正興, 鄧芳萍. 3種濾波算法對NDVI高質量數據保真性研究. 遙感技術與應用, 2010, 25(1): 118- 125.

[22]李紅軍, 鄭力, 雷玉平, 李春強, 周戡. 基于EOS/MODIS數據的NDVI與EVI比較研究. 地理科學進展, 2007, 26(1): 26- 32.

[23]劉珺, 田慶久, 黃彥, 杜靈通. 黃淮海夏玉米物候期遙感監測研究. 遙感信息, 2013, 28(3): 85- 90.

[24]張明偉. 基于MODIS數據的作物物候期監測及作物類型識別模式研究[D]. 武漢: 華中農業大學資源與環境學院, 200

Analysis of four time series EVI data reconstruction methods

LIU Yanan1,2,3, XIAO Fei1,2,*, DU Yun1,2

1InstituteofGeodesyandGeophysics,ChineseAcademyofSciences,Wuhan430077,China2KeyLaboratoryforEnvironmentandDisasterMonitoringandEvaluation,Wuhan430077,China3UniversityofChineseAcademyofSciences,Beijing100049,China

Time-series vegetation index data are contaminated with residual noise and cannot be used in land-cover change detection and crop yield estimation directly. To remove noise effectively, researchers have developed a series of methods for vegetation-index data reconstruction. Function curve-fitting methods are popular in the reconstruction of time-series vegetation index data and have been widely applied in many fields. Different function curve-fitting methods have specific adaptabilities to different geographical environments. In practice, researchers usually have to compare many function curve-fitting methods and select the most suitable one according to the characteristics of regional time-series vegetation index curve fluctuation. Therefore, the means of comparing different function curve fitting methods objectively and quantitatively is very important. Based on ten-year MODIS EVI data of evenly distributed sample areas and its quality control data from the Qinling Mountains, the evaluation method for EVI time-series data reconstruction was discussed and developed in this study. The new evaluation method can compare different function curve fitting methods objectively and quantitatively on two important aspects. One is the function curve-fitting effect under the disturbance of noise points, and another is the ability of retaining original high-quality data. In this study, we used EVI time series data of the sampling area in the Qinling Mountains to analyze the stability of the maximums and minimums of the EVI curves and found that the maximums are more stable in the EVI time series data than the minimums. Then we modified the form of the single logistic model on the basis of the above analysis. Finally, the Maximum optimization Logistic function fitting method (MSL) was proposed to improve the accuracy of the EVI time series reconstruction with large noise in complex mountains. In this study, a new evaluation method was used to compare the Asymmetry Gauss function fitting method (AG), Double Logistic function fitting method (DL), and Single Logistic function fitting method (SL) with the Maximum optimization Logistic function fitting method (MSL). The results show the following: (1) For the function curve fitting effect under the disturbance of the noise points while maintaining original high-quality data, AG showed better results in the treatment of several pixels. (2) Compared to the AG and DL, the fitting effect of SL and MSL is more significant. They not only undisturbed by the noise points but also have a stronger ability to maintain the original high-quality data than AG and DL. (3) Compared to the other methods, MSL was found to be more applicable for EVI time-series data reconstruction in complex mountains with large noise.

MODIS EVI; logistic curve fitting; time-series reconstruction; phenology; Qinling

國家自然科學基金資助項目(41271125)；國家重點基礎研究發展計劃項目(2012CB417001)

2015- 01- 07; 網絡出版日期:2015- 11- 16

Corresponding author.E-mail: xiaof@whigg.ac.cn

10.5846/stxb201501070054

劉亞南，肖飛，杜耘.基于秦嶺樣區的四種時序EVI函數擬合方法對比研究.生態學報,2016,36(15):4672- 4679.

Liu Y N, Xiao F, Du Y.Analysis of four time series EVI data reconstruction methods.Acta Ecologica Sinica,2016,36(15):4672- 4679.