兩輪自平衡小車的建模與控制

李楊，戰藝，周曉明，袁輝

（1.廣西大學機械工程學院，廣西南寧530004；2.廣西大學電氣工程學院，廣西南寧530004；3.深圳愛啃蘿卜機器人技術有限公司，廣東深圳518000）

兩輪自平衡小車的建模與控制

李楊1，戰藝1，周曉明2，袁輝3

（1.廣西大學機械工程學院，廣西南寧530004；2.廣西大學電氣工程學院，廣西南寧530004；3.深圳愛啃蘿卜機器人技術有限公司，廣東深圳518000）

兩輪自平衡小車利用狀態反饋法和串級PID控制實現其原地直立。對兩輪自平衡車進行建模，通過測量兩輪小車的實際物理參數，根據動力學、電氣關系建立系統的數學模型，運用設計控制算法來對兩輪小車實施控制并通過MATLAB來仿真控制效果。仿真和實驗結果表明：基于狀態空間表達式的控制器比基于傳遞函數的控制器有更好的控制效果和魯棒性。

自平衡小車；控制；仿真

兩輪自平衡車自身是個開環不穩定系統，具有狀態變量多、系統模型非線性、變量間強耦合等特點［1］。其控制方法主要有常規PID控制、自適應控制、模糊控制等［2］。本文通過經典控制理論和現代控制理論的知識實現對兩輪小車的控制，建立數學模型，確定其系統模型，采用串級PID控制，在MATLAB上仿真編寫控制程序，并在實物模型上驗證，通過驗證，確定基于狀態空間表達式的控制器比基于傳遞函數的控制器具有更好的控制效果和魯棒性［3］。

1　兩輪自平衡小車控制模型的建立

兩輪自平衡小車的抽象模型如圖1所示，小車整體由輪子和車體兩部分構成，其中車體由輪軸和擺桿組成。建立空間坐標系，α為擺桿與z軸夾角，β為輪軸與y軸夾角，即輪軸的初始位置與y軸重合，左輪指向右輪的方向為y軸的正向。擺桿傾斜時在地平面上的垂直投影與x軸重合，x軸的正向與擺桿傾斜的方向相同。輪軸的中點即空間坐標系的原點O，豎直向上為z軸的正方向［4］。

圖1　兩輪小車整體的抽象模型

由圖1建立自平衡小車的表達式：

如圖2、3分別為輪子和擺桿的受力分析圖。其中，θr分別為左右輪旋轉角度，xo為轉軸中點水平位移，zpxl為車身質心的豎直位移，L為擺桿質心到端點的長度，R為輪子半徑，D輪軸長度，Hr分別為左、右輪水平作用力，Pr為左、右輪豎直作用力，fr為左、右輪摩擦力，Vr、Vl分別為左右輪電壓。

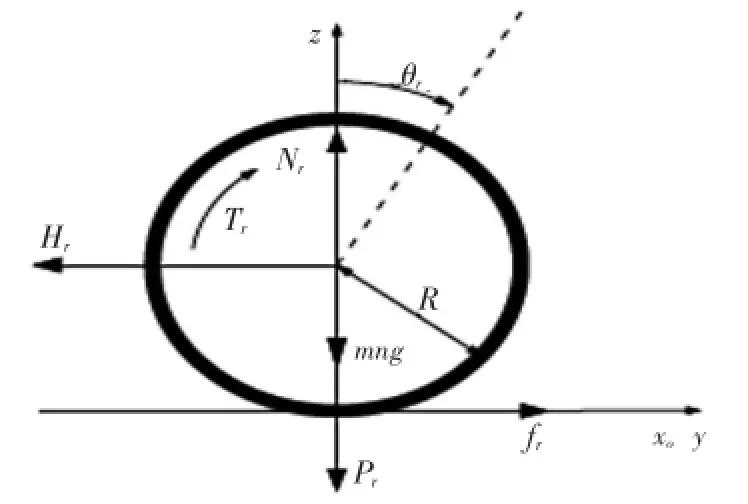
圖2　輪子的受力分析

圖3　擺桿的受力分析

由此可得其具體數值的狀態表達式：

2　仿真驗證

2.1開環穩定性

根據李雅普諾夫第一法判定兩輪小車開環系統是不穩定的［5］。為獲得開環系統的自由響應，輸出的空間表達式如公式為：

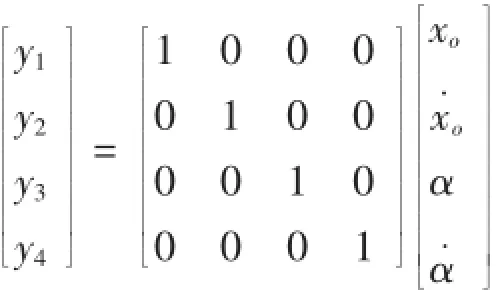
并使自平衡小車初始狀態為有一個α=1°的傾角可得：

系統的自由響應如圖4所示輸出圖像。

圖4　開環系統的非零自由響應

由圖像可知，在不到1 s的時間內，狀態變量及其導數逐漸向負方向移動。而狀態變量及其導數逐漸向正方向移動。且狀態變量移動的速度隨著時間推移越來越快。

仿真的結果與實物模型的動作是相符合的：小車在自由釋放后很快地失去平衡，在極短的時間內倒地，雙輪位置相比初始位置稍有后退，擺桿傾角在不到1 s內達90°.整個過程的各個狀態變量的變化隨著時間推進越來越快。具體數值由于已經超出了可線性化的區間意義不大。

2.2直立控制

由以上分析可知，兩輪小車是一個開環不穩定系統。為了對兩輪小車實現穩定控制，現根據兩輪小車的開環狀態表達式，通過狀態反饋的方式建立兩輪小車的閉環系統，從而改善系統的動態響應，使其受到任意的狀態擾動時，系統的狀態變量能很快地收斂到零。兩輪小車成為兩輪自平衡小車，并實現原地直立的控制目標。

令系統的初始狀態為［1 0 0 0］，通過很短的時間的自由響應，各個狀態變量收斂于零，系統的狀態變量曲線如圖5所示。

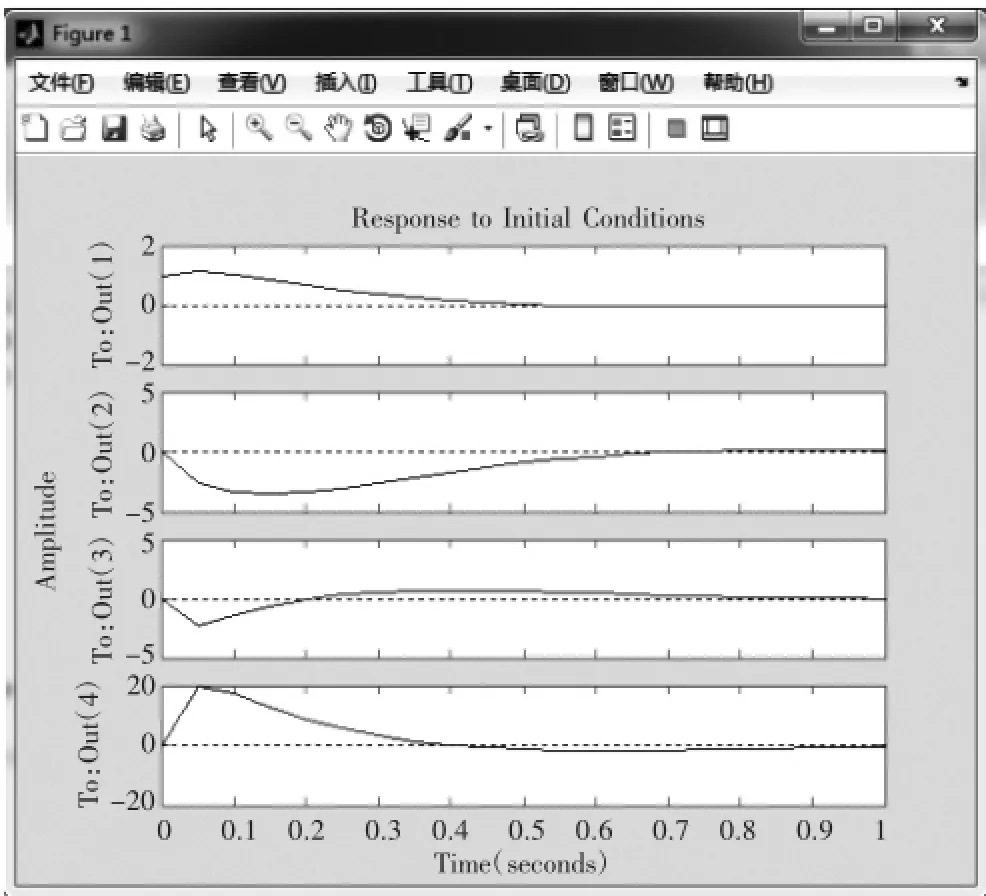
圖5　初始狀態［1 0 0 0］的自由響應

2.3速度控制

顯然，此時系統各個環節的傳遞函數都階數較高，這將導致系統的控制難度增大。然而根據實際經驗，采用PID控制器的雙閉環兩輪小車系統是完全能實現速度控制的（如圖6）。直接在實物模型上調試PID參數，并根據實際效果對系統結構優化，如圖7所示。優化的目的都在于保持角度環的參考輸入變化不劇烈并且不超出數學建模的線性化區間，從而確保兩路小車的基本平衡不被破壞。

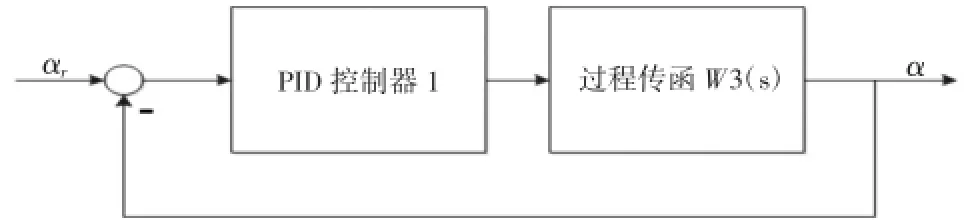
圖6　傾角閉環控制

圖7　優化后系統結構圖

經過優化后的速度控制算法通過在實物模型上驗證并微調參數，能達到很好的效果。速度控制的誤差滿足設計要求。

3　實物驗證

實現小車速度控制的關鍵在于維持小車傾角穩定，小車的傾角穩定通過PID算法實現。通過PID控制器的典型傳函對比可確認PID的三個參數，如圖8所示。

圖8　兩輪自平衡小車實物圖

使用狀態反饋法設計的控制器能使兩輪小車的原地直立具有較小的抖動，且無論受到何種干擾，小車都能較快地回復原平衡狀態。程序中，反饋的增益的設置與理論推導完全一致。在增益允許的條件下，將系統極點配置的盡可能地遠離虛軸能得到最好的控制效果。

而使用串級PID控制器控制兩輪小車，由于該控制器的控制對象是速度，令參考速度為零，也能實現直立的效果。但直立時的抖動要比前一種控制方式明顯，且當推動小車遠離原平衡位置時，其不能自動回到原位置平衡。

4　結束語

本文實現兩輪小車的控制，結果表明基于狀態空間表達式的控制器比基于傳遞函數的控制器具有更好的控制效果和魯棒性。

［1］劉莉宏.基于智能控制的PID控制方式的研究［J］.北京工業職業技術學院學報，2012，14（2）：33-38.

［2］屠運武，徐俊艷，張培仁，等.自平衡控制系統的建模與仿真［J］.系統仿真學報，2004，4（16）：83-84.

［3］Rich Chi Ooi.Balancing a Two-Wheeled Autonomous Robot［M］.Final Year Thesis of USQ，2003.

［4］劉李鋒.有源網絡結構能控性分析與設計［D］.武漢：武漢理工大學，2012.

［5］Vander Linden G W，Lambrcchts P F.H-∞control of an experimental inverted pendulum with dry friction［J］.IEEE control system magazine，1993，13（4）：44-5.

Modeling and Control of Two Wheeled Self-balancing Vehicle

LI Yang1，ZHAN Yi1，ZHOU Xiao-ming2，YUAN Hui3
（1.Guangxi University，School of Mechanical Engineering，Nanning Guangxi 530004，China；2.Guangxi University Electrical Engineering College，Nanning Guangxi 530004，China；3.Shenzhen Aicrobo Technology Co.，Ltd.，Shenzhen Guangdong 518000，China）

The standing upright of two wheel vehicle can be realized by state feedback method and cascade PID control.First，according to the physical model of the two wheel vehicle for abstract modeling，through the actual physical parameter of the measured two car，according to dynamics and electrical relationship established mathematical model of the system.In the mathematical model based on，according to the control design theory of control algorithm to control of two wheeled cart and by MATLAB to simulate control effect.The simulation results show that in the two kinds of vertical control method based on state space The expression controller has better control effect and robustness than that based on the transfer function of the controller.

self-balancing car；control；simulation

TP13

A

1672-545X（2016）08-0027-04

2016-05-11

李楊（1991-），男，山東萊蕪人，研究生，研究方向：機電液一體化。