不同濕潤比下滴灌土壤入滲特性模擬試驗研究

王　平，胡笑濤，王文娥

(西北農林科技大學 旱區農業水土工程教育部重點實驗室， 陜西 楊凌 712100)

?

不同濕潤比下滴灌土壤入滲特性模擬試驗研究

王平，胡笑濤，王文娥

(西北農林科技大學 旱區農業水土工程教育部重點實驗室， 陜西 楊凌 712100)

為了研究滴頭流量和設計濕潤比對土壤水分運移規律及濕潤體特性的影響，前期利用粘壤土進行試驗研究，然后依據非飽和土壤水動力學理論和滴灌條件下土壤水分運移特征，建立了土壤水分運動模型，利用HYDRUS-3D對不同濕潤比下滴灌土壤入滲模型進行求解。通過所建模型，對11個觀測點的模擬結果與實測結果進行了對比，得出灌水結束時各觀測點模擬與實測含水率的相對誤差均小于10%，實測與模擬濕潤比的相對誤差為4.75%～11.78%。利用所建模型對不同情景下濕潤體運移規律進行了模擬，獲得了濕潤體特征變化規律：滴頭流量主要影響水平濕潤鋒的運移距離，而設計濕潤比對垂直濕潤鋒運移距離的影響較大；滴頭流量相同時，設計濕潤比越大，濕潤體內平均含水率越大，高含水區(含水率>0.410 cm3·cm-3)半徑也越大； 設計濕潤比相同時，濕潤體內含水率高于0.410 cm3·cm-3的濕潤半徑隨流量增大而增大。

滴灌；濕潤比；入滲特性；土壤含水率；數值模擬

滴灌是目前最先進的局部灌溉方法之一，節水增產效果良好。與漫灌、噴灌等不同，滴灌屬于點源入滲，地表濕潤范圍及蒸發量小，灌溉水入滲主要集中在作物根系，有效提高了水分利用效率，由于土壤入滲速率與滴頭流量同時影響到土壤水分運動及分布，進一步影響作物根系對水分吸收，因此國內外許多學者都對滴灌條件下土壤水分運移規律及濕潤體特性進行了試驗研究[1-2]和數值模擬分析。Cote和Siyal都運用Hydrus-3D軟件對滴灌條件下的土壤水分及溶質運移進行了模擬和分析[3-4]；張林和魏群也利用Hydrus -3D模型對單點源和多點源滴灌條件下土壤水分運移進行了模擬試驗研究[5-6]。但是以上研究主要側重于滴頭流量、土壤特性、初始含水率對濕潤體的影響，很少涉及關于濕潤比對濕潤體特性的影響。濕潤比[7]是滴灌系統設計的一個重要參數，是把滴灌系統和作物生長的水分狀況聯系起來的重要紐帶。自Keller[8]提出濕潤比的概念后，濕潤比(Wetted percentage, WP)在滴灌系統的設計中得到了廣泛應用，雷廷武[9-10]根據濕潤比的定義，從理論上導出了濕潤比計算公式的理論基礎以及實際應用時應滿足的條件；晏清洪[11]通過采用3種滴灌濕潤比，探討了滴灌濕潤比對根系分布的影響。本文以不同濕潤比、滴頭流量的點源滴灌入滲試驗為基礎，利用HYDRUS-3D軟件對水分運移規律進行模擬，研究滴灌土壤水分的運移特征及含水率分布規律，為滴灌系統設計提供理論依據。

1　數值分析模型

1.1土壤水分運動方程

地表點源滴灌土壤水分運動屬于典型的三維問題，HYDRUS模型的水流狀態為飽和-非飽和達西水流，根據達西定律、質量守恒定律[12]，假定土壤均質、各向同性，忽略水分運動時空氣、溫度和滯后效應對土壤水分運動的影響，土壤水分運動用Richard方程來描述：

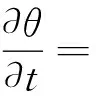
(1)

式中，φm為總水勢(MPa)；K(θ)為非飽和土壤導水率(cm·min-1)；θ為土壤體積含水率(cm3·cm-3)；t為水分運動時間(min)。

1.2定解條件

1.2.1初始條件求解土壤水分運動方程的初始條件[13]為：

h(x,y,z,t)=h0(x,y,z)0≤x≤X；

0≤y≤Y； 0≤z≤Z, t=0

(2)

式中，h(x,y,z,t)為計算區域的初始負壓水頭，cm；x、y、z分別為模擬計算區域水平長度、寬度和深度，根據土壤入滲試驗分別取x∈[0,30]、y∈[0,30]、z∈[0,70]，單位為cm。

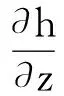
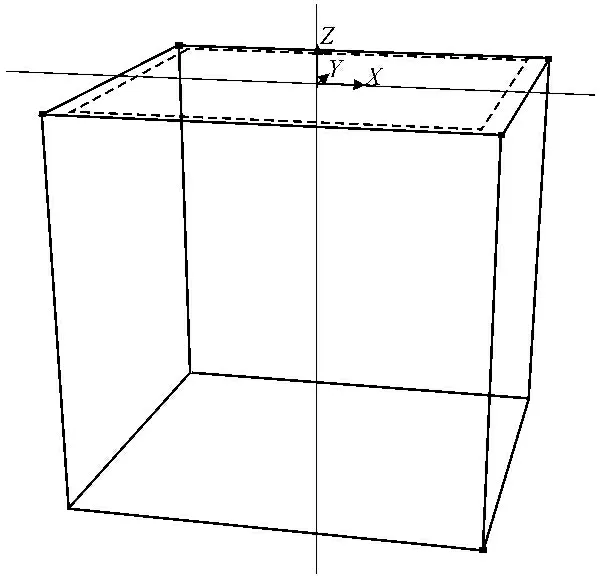
圖1數值模似計算區域

Fig.1Numerical simulation calculation region

上邊界是一個動態邊界，參考張林等[14]將上邊界分為兩種情況考慮：

(1) 滴頭流量較小，出流速率小于土壤的入滲速率，水分能夠瞬間滲入土壤中，即地表無積水。

在滴頭處有：

(3)

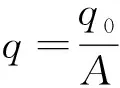
(2) 滴頭流量較大，出流速率大于土壤的入滲速率，水分不能迅速滲入土壤中，即地表有積水。

在地表飽和區有：

h=0 (0≤x≤Rs，X-Rs≤x≤X，z=0)

(4)

(5)

式中，Rs為地表積水半徑，cm。

模擬過程參考李久生[14]文獻中的方法：先假定地表積水的半徑，用數值模擬的方法來模擬水分運動(模擬灌水量與實際灌水量的誤差為5%左右)，將滴頭流量與時間的乘積近似為土體水量的增加，再通過數值模擬擬合地表積水半徑與滴頭流量的關系。

由于土箱深度較大，故下邊界可認為土壤水分和土壤壓力水頭保持不變，即：

h(x,y,z,t)=h0，0≤x≤X；t>0

(6)

1.3數值求解

采用商業軟件HYDRUS-3D對上述模型進行數值模擬，利用Galerkin有限單元法進行數學模型的數值計算[15]，利用隱式差分法對時間進行離散[16]。模型的模擬區域長、寬、高分別為60、60、70 cm的長方體，采用三棱柱進行單元網格劃分，網格大小為1.9 cm；滴頭附近由于土壤水勢梯度較大，對網格進行加密處理；為便于模擬結果的驗證，模擬時在沿滴頭位置處的1/4豎直剖面上設置了11個觀測點，相鄰觀測點的水平間距和垂直間距均為7.5 cm，觀測點具體布置如圖2所示。

圖2模擬區域觀測點布置

Fig.2 Layout diagram of observation points in simulation region

2　模型驗證

2.1供試土壤

供試土壤為陜西楊凌西北農林科技大學灌溉排水試驗站粘壤土，取土層次為0～40 cm。土壤容重為1.35 g·cm-3，土壤的機械組成為砂粒(0.02 mm)占62.00%，粉粒(0.002～0.02 mm)占32.36%，粘粒(<0.002 mm)占5.64%，土樣風干后過2 mm篩備用。

土壤水分特征曲線利用高速離心機測定，土壤飽和導水率用定水頭法進行測定，土壤水分特征曲線采用Van Genuchten模型擬合。

(7)

(8)

其中：

Se=(θ-θr)/(θs-θr)

(9)

m=1-1/n, n>1

(10)

式中，θs為土壤飽和導水率(cm3·cm-3)；θr為土壤殘余含水率(cm3·cm-3)；α,n,m為擬合參數；α是與土壤物理性質有關的參數(cm-1)。h為土壤負壓水頭(cm)；Ks為滲透系數(cm·min-1)；Se為土壤有效含水率(cm3·cm-3)；l為空隙連通性參數，一般情況取為0.5。本研究中土壤水分特性的參數值為θr=0.03cm3·cm-3；θs=0.48cm3·cm-3；α=0.036cm-1；n=1.56；Ks=0.125cm·min-1。

2.2試驗裝置與方法

通過室內單點源滴灌入滲試驗，對所建數學模型進行驗證。試驗裝置由供水系統、有機玻璃土箱和土壤水分測定儀ECH2O組成。供水系統由恒定水頭為10 m的水塔和滴頭組成，滴頭為兩種以色列NETAFIM管上式壓力補償滴頭，利用水塔向滴頭供水，滴頭實測流量分別為2.2 L·h-1和4.1 L·h-1；有機玻璃土箱尺寸為60 cm×60 cm×70 cm(長×寬×高)；試驗過程中采用ECH2O土壤水分測定儀實時監測土壤濕潤體內含水率的動態變化，ECH2O由傳感器和數據采集器兩部分組成。

試驗土壤按照容重1.35 g·cm-3分層裝土，底層裝土厚度為10 cm，上面每層為7.5 cm，裝土過程中埋設傳感器，共40個，傳感器布置圖如圖3所示，傳感器的橫向與垂向距離均為7.5 cm；裝土結束后自然沉降一天以獲得均勻穩定的土壤初始含水率。

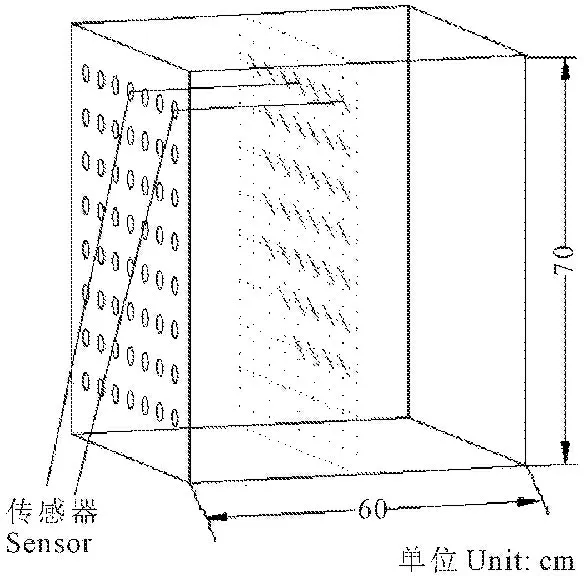
圖3傳感器布置

Fig.3Arrangement diagram of sensor

試驗在相同土壤初始含水率(7%)和相同土壤容重(1.35 g·cm-3)的條件下，分別選擇滴頭流量為2.2、4.1 L·h-1，設計濕潤比為40%、60%、80%水平下開展試驗。試驗于2014年4—6月在陜西楊凌西北農林科技大學旱區農業水土工程教育部重點實驗室進行，試驗開始后通過數據采集器監測48 h內濕潤體的含水率變化情況，觀測時間間隔為2 min。

2.3結果驗證

2.3.1土壤含水率表1列出了灌水結束時60%濕潤比、滴頭流量2.2 L·h-1時，11個觀測點實測與模擬土壤含水率的對比結果。由表1可以看出，土壤含水率的實測值與模擬值之間相對誤差的絕對值在1.6%～10%之間，此外還可以看出距離滴頭越遠，含水率的相對誤差越大，這可能是由于模擬是在土壤均質、各向同性的理想情況下進行，而實際試驗時沉降過程中下層土壤會比上層土壤壓實程度大，進而減小了土壤下層水分運移速率，導致實測與模擬含水率之間差值變大。但從總體來看，數值模擬的結果與試驗結果基本一致，說明利用所建立的數學模型可以對滴灌的土壤水分運移進行模擬。

2.3.2土壤含水率隨時間的變化規律圖4為灌水結束時，不同處理下的3個觀測點處含水率隨時間變化規律的模擬與實測對比情況。從圖中可以看出，灌水開始后，觀測點距離滴頭越近，該觀測點的含水率增長速度越快，隨著時間推移，含水率增長速度逐漸趨于平緩，總的來看，各觀測點處的含水率都呈先增大后趨于平緩的趨勢。通過模擬值與實測值對比，可知模擬和實測的含水率變化規律基本一致，各觀測點的模擬值與實測值均較接近，相對誤差(相對誤差=|模擬值-實測值|/實測值)均小于10%，模擬結果能較好地反映濕潤體內含水率的變化情況。

表1　土壤含水率實測值與模擬值的對比

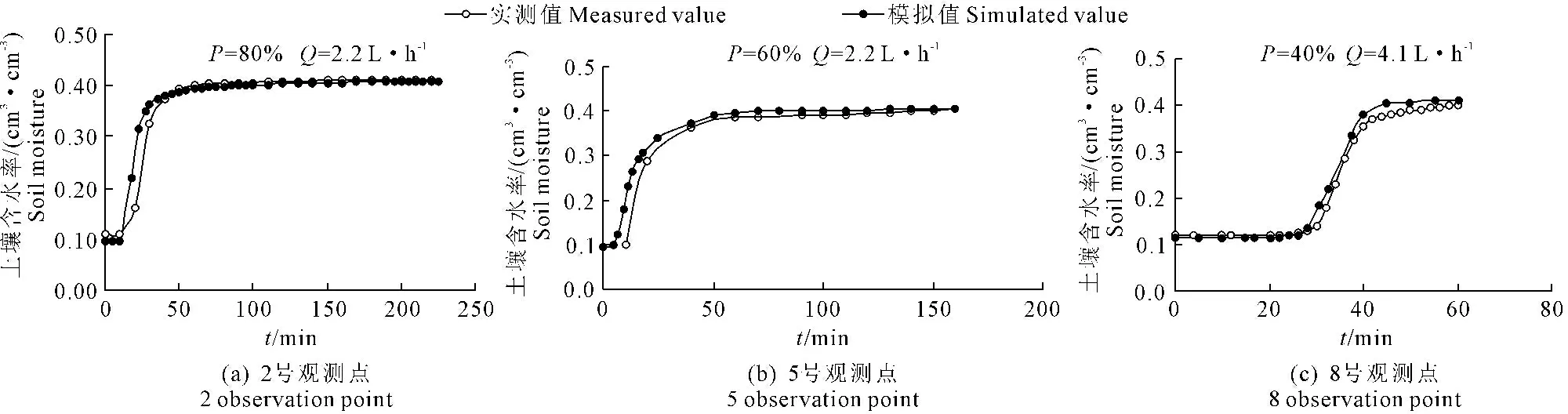
圖4土壤含水率試驗值與模擬值對比

Fig.4Comparison of measured and simulated soil moisture

2.3.3濕潤比的變化規律表2給出了灌水結束時，不同處理下實際與模擬濕潤比的對比情況，由表中可以看出，模擬濕潤比均稍大于實際濕潤比，實際與模擬濕潤比的相對誤差變幅在4.75%～11.78%之間，誤差原因可能是由于裝土階段土壤夯實不均勻或由于儀器測量誤差造成的。總體來看，模擬結果仍可以很好地代表實測結果，表明所建模型可用于實際濕潤比的計算。

3　結果與分析

利用所建模型對濕潤比分別為40%、50%、60%、70%、80%，滴頭流量分別為2.2、3.0、4.1、5.0 L·h-1情況下濕潤體的運移特征進行了模擬，并分析了模擬結果的濕潤體特性變化規律。

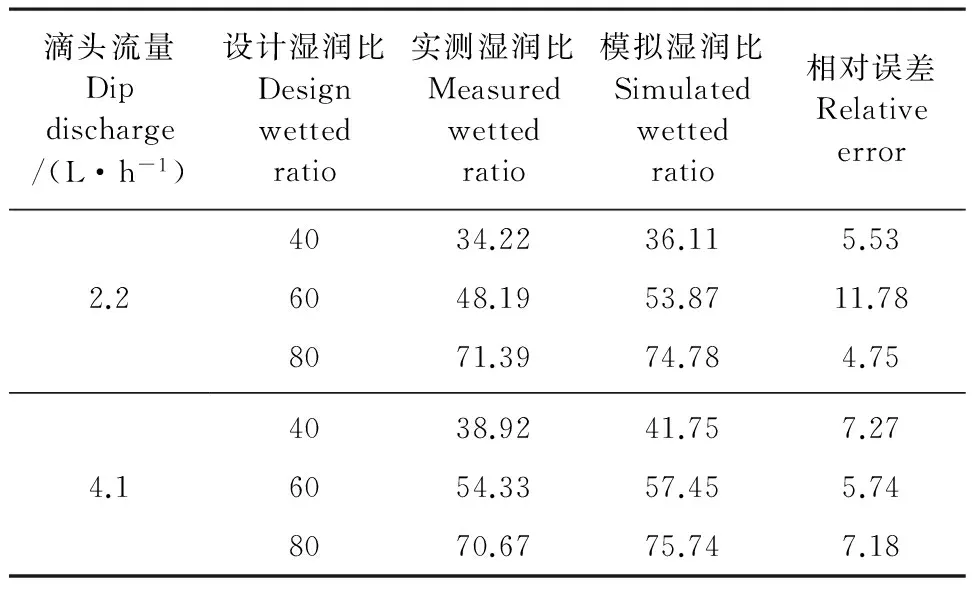
表2　濕潤比實測值與模擬值的對比/%

3.1流量和設計濕潤比對濕潤體形狀的影響

表3為模擬的不同設計濕潤比和滴頭流量下濕潤體的深寬比(H/x，濕潤體在垂直方向運移距離與水平方向運移距離的比值)變化規律。由表3可以看出，相同設計濕潤比時，深寬比隨滴頭流量增大而減小，說明滴頭流量對水平運移距離的影響較大，滴頭流量較小時(2.2、3 L·h-1)，濕潤鋒的垂直運移距離大于水平運移距離，這是因為滴頭流量越大，土壤入滲能力越小于供水強度，土壤表層積水半徑越大，加速了積水區在水平方向的運移速率；滴頭流量相同時，深寬比隨設計濕潤比的增大而增大，這說明設計濕潤比對垂直方向運移距離的影響大于對水平方向運移距離的影響，這是由于同一滴頭流量不會影響濕潤鋒在水平方向的擴散速率，但隨著設計濕潤比增大，灌水時間延長，而土水勢梯度又隨時間推移逐漸減小，在重力勢和基質勢共同作用下，土壤水分在垂直方向運移速率增大。因此滴頭流量主要影響濕潤體的水平運移距離，而設計濕潤比主要影響濕潤體的垂直運移距離。

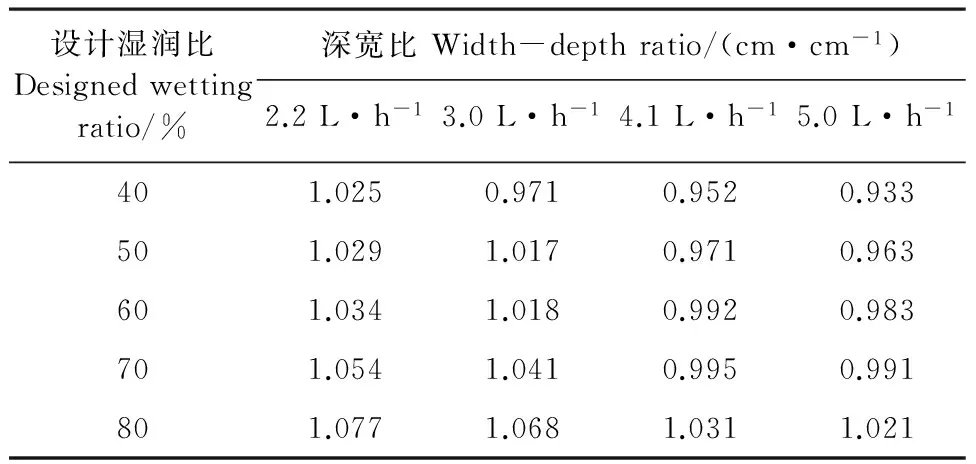
表3　不同設計濕潤比下滴頭流量對濕潤體深寬比的影響

3.2設計濕潤比對土壤水分分布的影響

設計濕潤比的選取對滴灌的灌溉效果有很大影響，圖5為灌水結束時，4.1 L·h-1滴頭流量、不同設計濕潤比下的土壤水分分布情況。從圖中可以得出，入滲所形成的濕潤體剖面均為1/4橢圓形，隨設計濕潤比增大，入滲的水平和垂直距離逐漸變大，濕潤體體積也相應變大。

設計濕潤比越大，濕潤體內高含水區(含水率>0.410 cm3·cm-3)半徑也越大，例如設計濕潤比為40%時，高含水區表層半徑為13 cm，而當設計濕潤比為80%時，高含水區表層半徑達到16 cm；設計濕潤比逐漸增大時，濕潤體內的平均含水率也依次增大，分別為0.251、0.256、0.262、0.268、0.272 cm3·cm-3，這是由于隨著濕潤比增大，雖然灌水量變大，但濕潤體積也會相應增大，導致濕潤體內的平均含水率變化較小。因此，對含水率值無太大要求的情況下，適當地減小設計濕潤比，可以達到節水效果，而且幾乎不會影響濕潤體內的平均含水率大小。

3.3滴頭流量對土壤水分分布的影響

滴頭流量影響濕潤體的大小、形狀和土壤水分分布的不均勻程度，將對作物生長產生影響[17]。圖6為灌水結束時設計濕潤比為60%、不同滴頭流量下濕潤體內的含水率分布情況，圖為濕潤體的1/4剖面。

由圖6可以看出滴頭流量不同時，濕潤體大小隨滴頭流量增大有小幅度的增加。以滴頭流量分別為2.2 L·h-1和4.1 L·h-1為例，滴頭流量為2.2 L·h-1時實際濕潤比為53.87%，而滴頭流量為4.1 L·h-1時實際濕潤比為57.45%，增長幅度僅為6.65%；濕潤體內高含水區表層半徑隨滴頭流量增大而增大，滴頭流量逐漸增大時，濕潤體內含水率高于0.410 cm3·cm-3的濕潤半徑分別為11、13、15、16 cm，這是因為設計濕潤比相同時，滴頭流量越大，灌水時間越短，地表附近的灌水無法及時下滲，形成積水區的范圍也會變大，濕潤體內的高含水區的范圍也相應增大；由于濕潤體大小隨滴頭流量的增大而增大，因此在設計濕潤比相同情況下，滴頭流量的增大反而會減小濕潤體內的平均含水率，從而有可能在滴頭流量較大時，濕潤體內的含水率無法滿足作物的生長需求。

4　結　論

本文根據非飽和土壤水動力學理論和單點源滴灌條件下土壤水分運移特征，按照試驗條件設定邊界，建立了單點源滴灌條件下土壤水分運動數學模型，并用商業化HYDRUS-3D軟件對模型進行了數值求解。通過對3種設計濕潤比、2種流量條件下滴灌土壤水分隨時間變化規律的模擬值與實測值進行對比可知：

1) 灌水結束時，觀測點處模擬與實測含水率的相對誤差均在10%以內；實測與模擬濕潤比的相對誤差變幅為4.75%～11.78%，總體上模擬結果可以很好地代表實測結果，表明所建模型可用于對實際入滲特性的模擬計算。

2) 滴頭流量對濕潤鋒水平運移距離的影響較大，設計濕潤比主要影響濕潤鋒在垂直方向的運移距離；相同滴頭流量(4 L·h-1)時，設計濕潤比越大，濕潤體內平均含水率越大，且濕潤體內高含水區(含水率>0.410 cm3·cm-3)半徑也越大；設計濕潤比相同(60%)，滴頭流量不同時，濕潤體大小隨滴頭流量

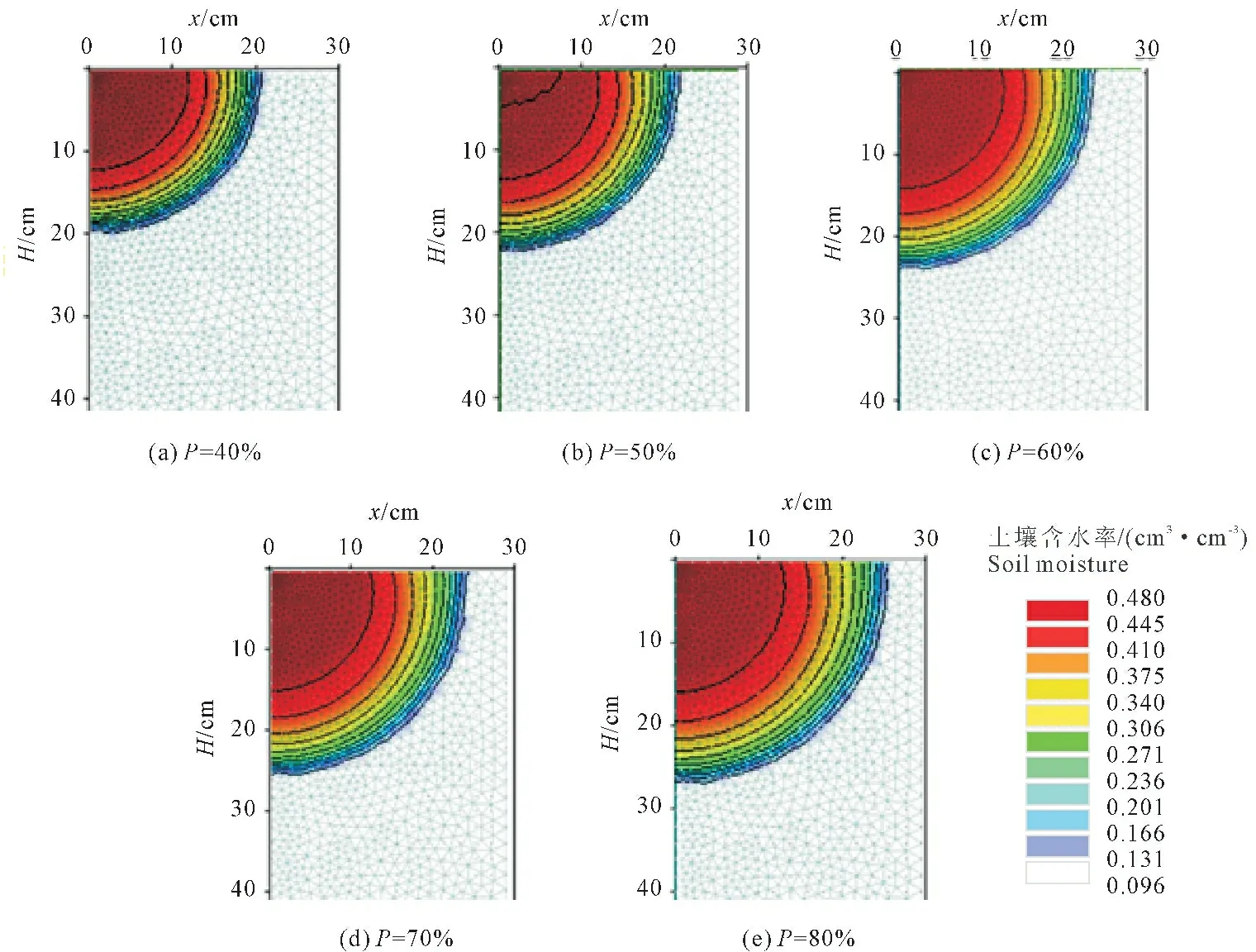
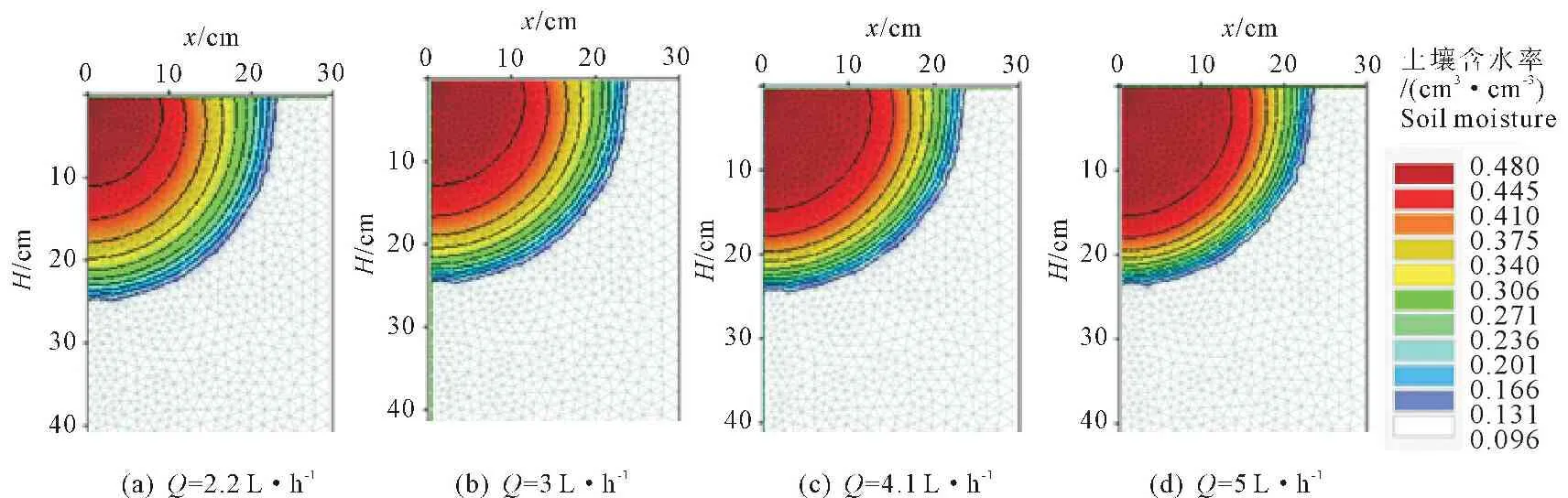
圖5　設計濕潤比對土壤水分分布的影響

圖6滴頭流量對土壤水分分布的影響(模擬)

Fig.6Effects of dripper discharge on soil water distribution (simulation)

增大有小幅度增加，濕潤體內含水率高于0.410 cm3·cm-3的半徑隨滴頭流量的增大而增大，但是滴頭流量增大反而會降低濕潤體內的平均含水率。

實際指導灌溉時，應結合作物根區分布情況，合理地選擇滴頭流量和設計濕潤比，使水分不至于造成無效蒸發和深層滲漏，例如滴灌條件下種植棉花、蔬菜等經濟作物，根系在垂直方向主要分布在0～30 cm土層，在水平方向是由作物植株處向兩側逐漸減小，適宜選擇較小的設計濕潤比和較大的滴頭流量，既不會造成深層滲漏，也可以達到很好的濕潤效果。

[1]張振華,蔡煥杰,郭永昌，等.滴灌土壤濕潤體影響因素的實驗研究[J].農業工程學報,2002,18(2):17-20.

[2]李道西,代小平,馮江,等.滴頭流量和灌水量對滴灌土壤水分運動的影響[J].節水灌溉,2012,(2):13-15.

[3]Cote C M, Bristow K L, Charlesworth P B, et al. Analysis of soil wetting and solute transport in subsurface trickle irrigation[J]. Irrigation Science, 2003,22(3/4):143-156.

[4]A. A. Siyal, T. H. Skaggs. Measured and simulated soil wetting patterns under porous clay pipe sub-surface irrigation[J]. Agricultural water Management, 2008,96(6):893-904.

[5]張林,吳普特,朱德蘭,等.多點源滴灌條件下土壤水分運移模擬試驗研究[J].排灌機械工程學報,2012,30(2):237-243.[6]魏群,費良軍.地表滴灌點源入滲土壤水分運動的模擬研究[J].廣東水利水電,2012,(z1):7-10,15.

[7]傅琳,董文楚,鄭耀泉.微灌工程技術指南[M].北京:水利電力出版社,1988:96-100.

[8]Keller J, Karmeli D. Trickle irrigation design parameters[J]. Transaction of the ASAE, 1974,17(4):678-684.

[9]雷廷武,鄭耀泉,聶光鏞.滴灌濕潤比的有理設計方法及應用[J].農業工程學報,1992,8(1):23-34.

[10]雷廷武.滴灌濕潤比的解析設計[J].水利學報,1994,(1):1-9. [11]晏清洪,王偉,任德新,等.滴灌濕潤比對成齡庫爾勒香梨生長及耗水規律的影響[J].干旱地區農業研究,2011,29(1):7-13.[12]李光永,鄭耀泉,曾德超,等.地埋點源非飽和土壤水運動的數值模擬[J].水利學報,1996,27(11):47-56.

[13]張林,吳普特,范興科.多點源滴灌條件下土壤水分運動的數值模擬[J].農業工程學報,2010,26(9):40-45.

[14]李久生,張建君,饒敏杰.滴灌施肥灌溉的水氮運移數學模擬及試驗驗證[J].水利學報,2005,36(8):932-938.

[15]Liping Pang, Murray E Close, James P.C Watt, et al. Simulation of picloram, atrazine, and simazine leaching through two New Zealand soils and into ground water using HYDRUS-2D[J]. Journal of Contaminant Hydrology, 2000,44(1):19-46.

[16]Prit Pal Singh Lubana, N.K. Narda. Soil water dynamics model for trickle irrigated tomatoes[J]. Agricultural Water Management, 1998,37(2):145-161.

[17]李明思,康紹忠,孫海燕.點源滴灌滴頭流量與濕潤體關系研究[J].農業工程學報,2006,22(4):32-35.

Simulation of soil infiltration characteristics under different wetted soil percentage

WANG Ping, HU Xiao-tao, WANG Wen-e

(KeyLaboratoryofAgriculturalSoilandWaterEngineeringinAridandSemiaridAreas,MinistryofEducation,NorthwestA&FUniversity,Yangling,Shaanxi712100,China)

Designed wetted percentage and dripper discharge are two important parameters in the design of drip irrigation system, affecting the size of wetted body and growth status of plant. With the aim of elucidating the influence of dripper discharge and thereby designing wetted percentage according to soil moisture migration and wetting soil characteristic, this paper based on the theory of unsaturated dynamics and the characteristics of soil moisture transfer under drip irrigation, and established a model of soil water movement, HYDRUS-3D software, to solve the soil infiltration model under different wetted soil percentage. The contrast of measured and simulated values showed that at the end of irrigation, the relative error between simulated and measured values of each observation point were less than 10%, and those for wetted soil percentage were 4.75%～11.78%. By simulating the wetted soil moisture migration under different condition using the established model, we obtained the rule of wetting body characteristics. Dripper discharge mainly affected the migration distance in horizontal direction, design wetted soil percentage had a greater influence on vertical direction. When the dipper discharge is the same, the larger the design wetted soil percentage, the greater the average moisture content in wetted body and the bigger radius of high water zone (water content>0.410 cm3·cm-3). When the design wetted percentage was the same, the radius of high water cut in wetted body increased as the dripper discharge increased.

drip irrigation; wetted percentage; infiltration characteristics; soil water content; numerical simulation

1000-7601(2016)04-0006-06

10.7606/j.issn.1000-7601.2016.04.02

2015-09-10

國家自然科學基金項目(51179163)

王平(1989—)，女，河北滄州人，碩士研究生，主要從事節水灌溉原理與新技術研究。 E-mail:1092443775@qq.com。

胡笑濤(1972—)，男，博士，教授，主要從事節水灌溉理論與新技術研究。 E-mail:huxiaotao11@nwsuaf.edu.cn。

doi:10.7606/j.issn.1000-7601.2016.04.02

S275.6

A

文章編號：1000-7601(2016)04-0006-06

收稿日期：2015-09-10

基金項目：國家自然科學基金項目(51179163)

作者簡介：王平(1989—)，女，河北滄州人，碩士研究生，主要從事節水灌溉原理與新技術研究。 E-mail:1092443775@qq.com。

通信作者：胡笑濤(1972—)，男，博士，教授，主要從事節水灌溉理論與新技術研究。 E-mail:huxiaotao11@nwsuaf.edu.cn。