基于馬爾科夫—Verhulst模型的鐵路貨運量預測研究
袁勝強,鮑學英,王起才
(蘭州交通大學土木工程學院,蘭州 730070)
?
基于馬爾科夫—Verhulst模型的鐵路貨運量預測研究
袁勝強,鮑學英,王起才
(蘭州交通大學土木工程學院,蘭州730070)
鐵路貨運量是一個地區經濟發展的先行指標之一,準確預測鐵路貨運量能夠為該地區的發展規劃起到指導作用。針對傳統灰色Verhulst模型在進行鐵路貨運量預測時模型誤差較大的問題,運用馬爾科夫鏈模型對傳統Verhulst模型的預測結果進行修正改進,以提高模型的預測精度。最后,通過引入實際案例,驗證了經過馬爾科夫鏈改進的灰色Verhulst模型在預測精度方面有了大幅度的提高,適用于甘肅省鐵路貨運量的預測。因此,應用該模型對甘肅省2015年到2017年的鐵路貨運量進行預測,為該地區的物流運輸及其他相關行業的發展提供可靠的指標依據。
物流運輸;鐵路貨運量;Verhulst模型;馬爾科夫鏈模型;預測
鐵路貨運是一個地區交通運輸的重要組成部分,更是這一地區經濟發展和居民生活所必需的,它不僅為該地區物流業提供便利,而且影響著該地區人民生活的各個方面。能夠系統準確地預測鐵路貨運量將會給該地區經濟發展提供一個有力的指標,并為鐵路運輸所帶來的環境影響提供可靠的數據分析。目前對于貨運量預測的方法種類很多,在國內研究方面,耿立艷等[1]運用了灰色關聯分析法、回歸預測法,趙闖等[2-3]運用了人工神經網絡等新型智能算法。吳華穩[4]成功地將混沌時間序列法應用到了鐵路貨運預測中,國外研究中,許多學者提出了多種對貨運量的預測方法,建立了混沌神經網絡貨運量預測模型[5],提出了遞歸神經網絡預測模型[6],采用混沌時間序列多變量預測模型[7],結合神經網絡并對混沌時間序列作出預測分析[8]。
通過以上研究可以發現,合理選擇方法雖能夠得到精度相對較高的預測,但仍然缺少改進,因此通過分析預測對象及各種預測方法的優缺點,進行模型的結合及改進才能夠保證預測的精度。本文以甘肅省2000年—2014年的鐵路年總貨運量數據(包括發送量和到達量)為基礎,對數據進行分析并結合前文所述提出了一種精度較高的改進模型對未來三年的鐵路貨運量進行預測,即運用馬爾科夫鏈對Verhulst模型的預測值進行改進,該模型既利用灰色Verhulst模型具有樣本數據量小、運算原理簡單、短期預測精度相對較高的特點,又結合了馬爾科夫鏈具有預測狀態劃分得出區間概率的特點,通過實例分析得出該結論可行。
1 灰色Verhulst模型的建立[9]
(1)非負原始數列為:X(0)={x(0)(1),x(0)(2),…,x(0)(n)}
對X(0)作一次累減得:X(1)={x(1)(1),x(1)(2),…,x(1)(n)}
其中:x(1)(k)=x(0)(k)-x(0)(k-1)x(1)(1)=x(0)(1)k=(1,2,…,n)
(2)生成X(1)的緊鄰均值數列
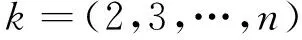
此時稱:X(0)+aZ(1)=b(Z(1))2為灰色verhulst模型,其微分方程為
(1)
式中,t為時間;a,b為待定參數。
此微分方程的解為
(2)
時間響應式
(3)
規定x(0)(1)=x(1)(1),累減還原,得到了原始序列的灰色Verhulst預測模型為
(4)
(3)確定Verhulst預測模型的參數。a,b為待估計參數向量,用最小二乘求解
即可解出參數a,b的值。
2 馬爾科夫鏈建模過程[11]
(1)建立一步狀態轉移矩陣
pij為由馬爾科夫鏈狀態Si轉移到Sj的概率。
mi為狀態Si出現的次數,mij為狀態Si轉移Sj到的次數。
(3)馬爾可夫鏈預測模型:A(n)=A(0)Pn
A(n)為n時刻的狀態概率向量,A(0)為初始時刻的狀態概率向量。
對于Verhulst模型得到的預測結果,可以根據馬爾科夫鏈的方法獲得Verhulst模型在已知年份的偏差規律(即偏差的狀況轉移矩陣)[13],并且依照此規律對Verhulst模型結果進行修正,由Verhulst模型結果的一個預測數值,修正成為區間和概率組成的預測范圍,增加預測的可信性,這就是馬爾科夫鏈改進方法的基本思路。
3 案例應用
以國家統計局資料中甘肅省2003年至2014年鐵路年貨運量數據為預測樣本,運用灰色Verhulst模型進行預測,再運用馬爾科夫鏈改進預測精度高的模型。數據見表1。
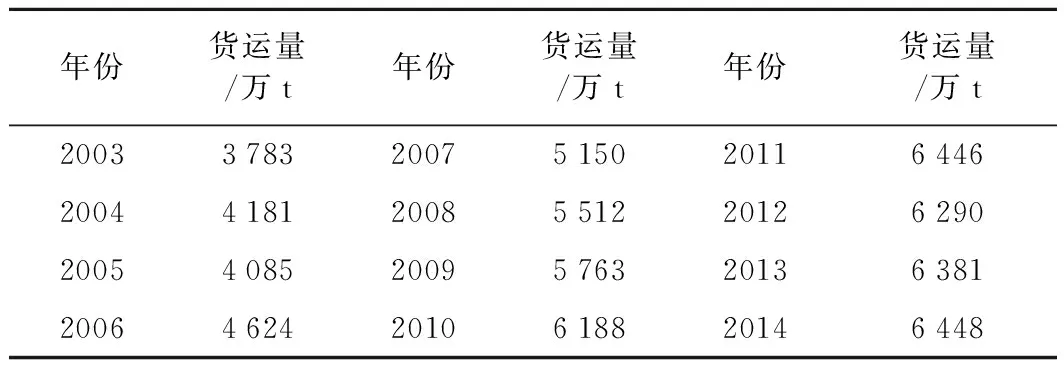
表1 甘肅省2003年至2014年鐵路貨運量
(1)設原始數據為
X(0)={3 783,4 181,4 085,4 624,5 150,5 512,5 763,6 188,6 446,6 290,6 381,6 448}
(2)累減序列為
X′(1)={3 783,398,-96,539,526,362,251,425,258,-156,91,67}
(3)緊鄰均值生成序列
Z(1)={3 982,4 133,4 354.5,4 887,5 331,5 637.5,5 975.5,6 317,6 368,6 335.5,6 414.5}
(4)在Verhulst模型中,計算得:a=-0.216 6b=-0.000 03
得到其時間響應式為
預測結果見表2。
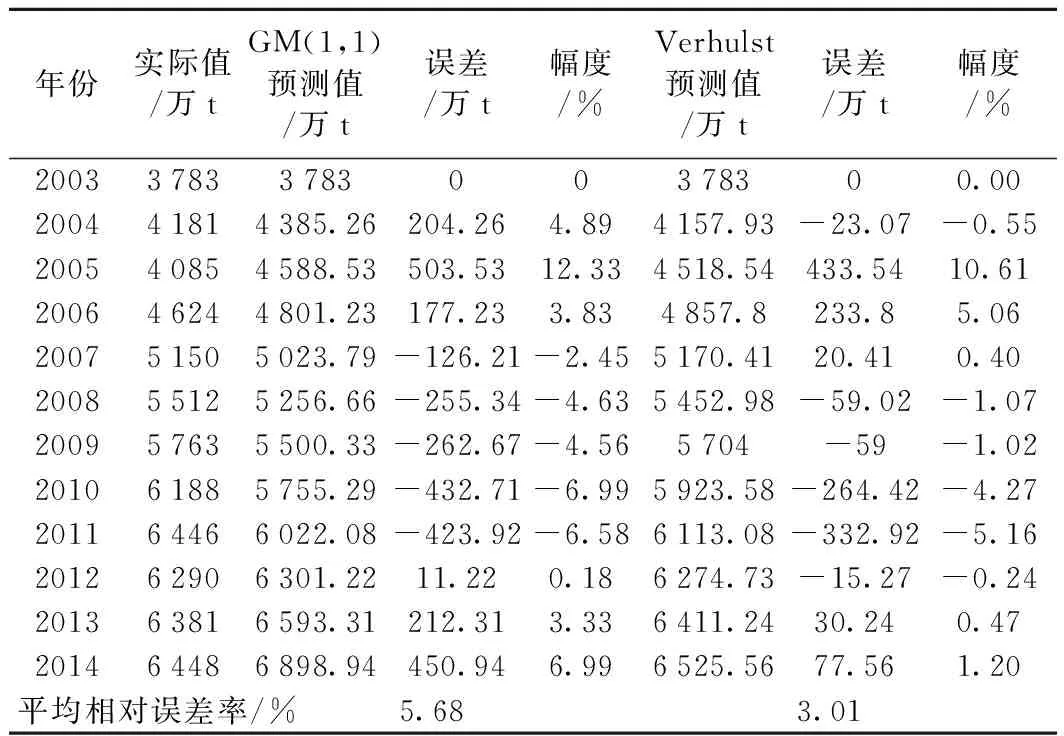
表2 甘肅省2003年至2014年鐵路貨運量預測
引入GM(1,1)模型[14]的預測數據作為對比發現,Verhulst模型擬合的預測值精度要比灰色GM(1,1)模型預測的高,所以選用2003年到2012年貨運量的Verhulst模型預測值為基礎數據建立馬爾科夫鏈模型并改進Verhulst模型預測值,與原始數據做對比,檢驗組合模型的改進精度。若改進模型精度提高,證明可行,可繼續用Verhulst模型預測甘肅省2015~2017年的鐵路貨運量,并建立馬爾科夫鏈進行改進。
(5)馬爾科夫鏈狀態轉移矩陣的獲得
根據馬爾科夫鏈分析方法的應用經驗和實際情況,按照年鐵路貨運量的增幅,可以劃分為5種狀態[15]:
①極高估狀態:即誤差幅度大于10%的狀態,僅有1年(2005);
②高估狀態:即誤差幅度在2%~10%之間的狀態,僅有1年(2006);
③穩定狀態:即誤差幅度在-2%~2%之間的狀態,有8年(2003,2004,2007,2008,2009,2012,2013,2014);
④低估狀態:即誤差幅度在-2%~10%之間,有2年(2010,2011);
⑤極低估狀態:即誤差幅度小于-10%的狀態,沒有此種狀態。
得出2003~2012年的狀態轉移矩陣見表3。
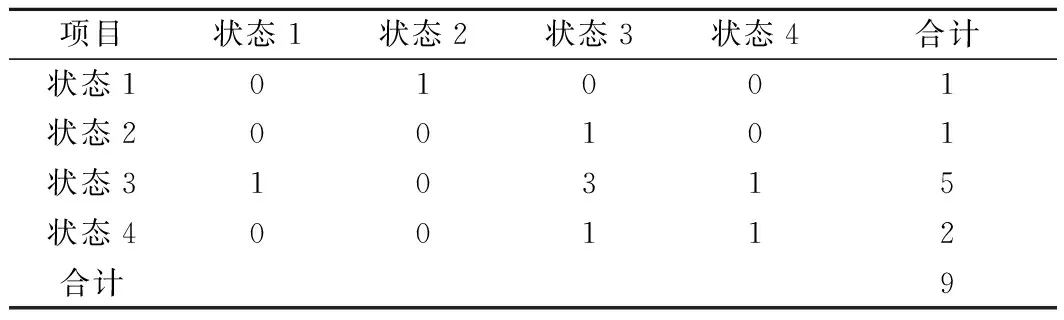
表3 馬爾科夫狀態轉移(2003~2012)
得到一步轉移狀態矩陣
根據馬爾可夫鏈預測原理,得到原始數據之后2年(2013~2014)的預測狀態向量
A(0)為原始向量,即2012年的狀態向量,由表2知2012年預測值誤差幅度為-0.24%,屬于狀態③,則狀態向量為[0,0,1,0],可得2013~2014年貨運量預測狀態向量
馬爾科夫鏈改進后的貨運量預測值(2013~2014)見表4。
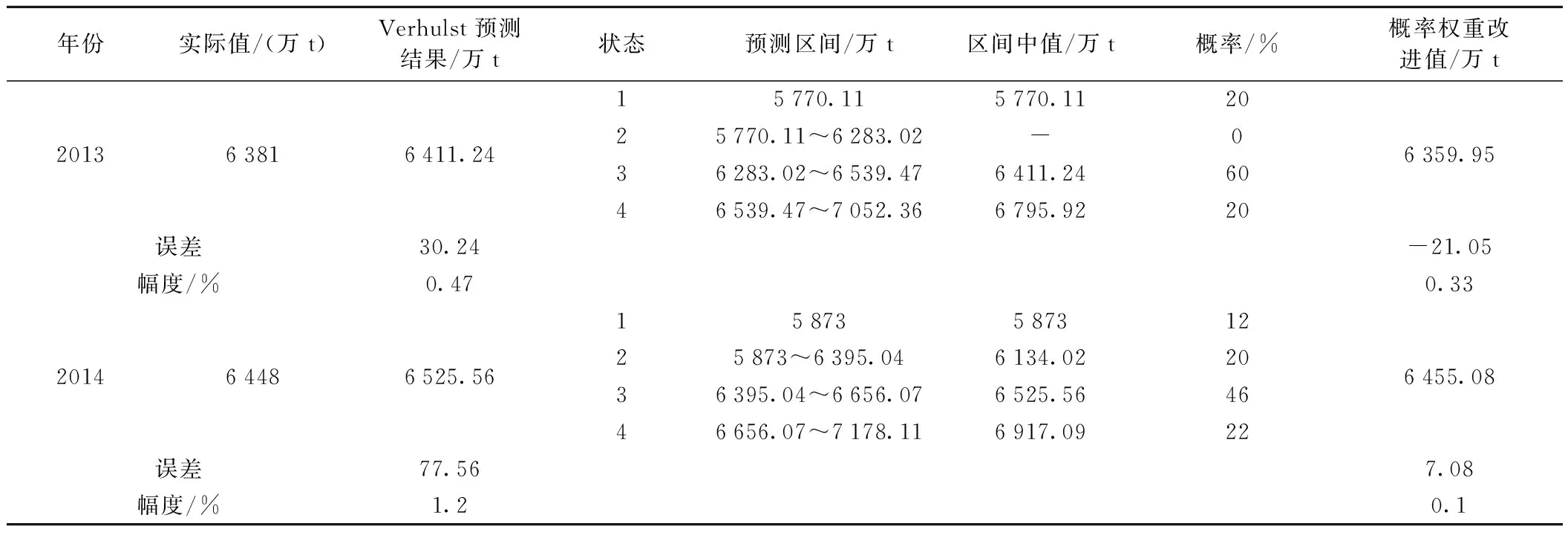
表4 馬爾科夫鏈改進后的貨運量預測值(2013~2014)
通過表4可以得出:經過馬爾科夫鏈改進后,2013年和2014年鐵路貨運量預測值的誤差和幅度均小于Verhulst模型的預測值,證明改進后的模型預測精度有所提高。可用于2015~2017年鐵路貨運量的預測。馬爾科夫狀態轉移見表5。
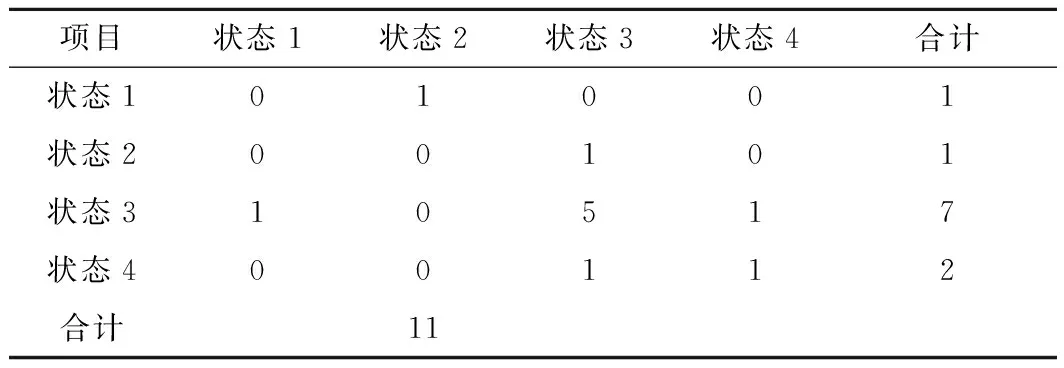
表5 馬爾科夫狀態轉移(2003~2014)
可得到一步轉移狀態矩陣

根據馬爾可夫鏈預測原理,得到原始數據之后3年(2015~2017)的預測狀態向量
A(0)為原始向量,即2014年的狀態向量,由表2知2014年預測值誤差幅度為1.2%,屬于狀態③,則狀態向量為[0,0,1,0],得2015~2017年貨運量預測狀態向量
A2015=[0.14,0,0.72,0.14]
A2016=[0.1,0.14,0.59,0.17]
A2017=[0.08,0.1,0.65,0.17]
馬爾科夫鏈改進后的貨運量預測值(2015~2017)見表6。
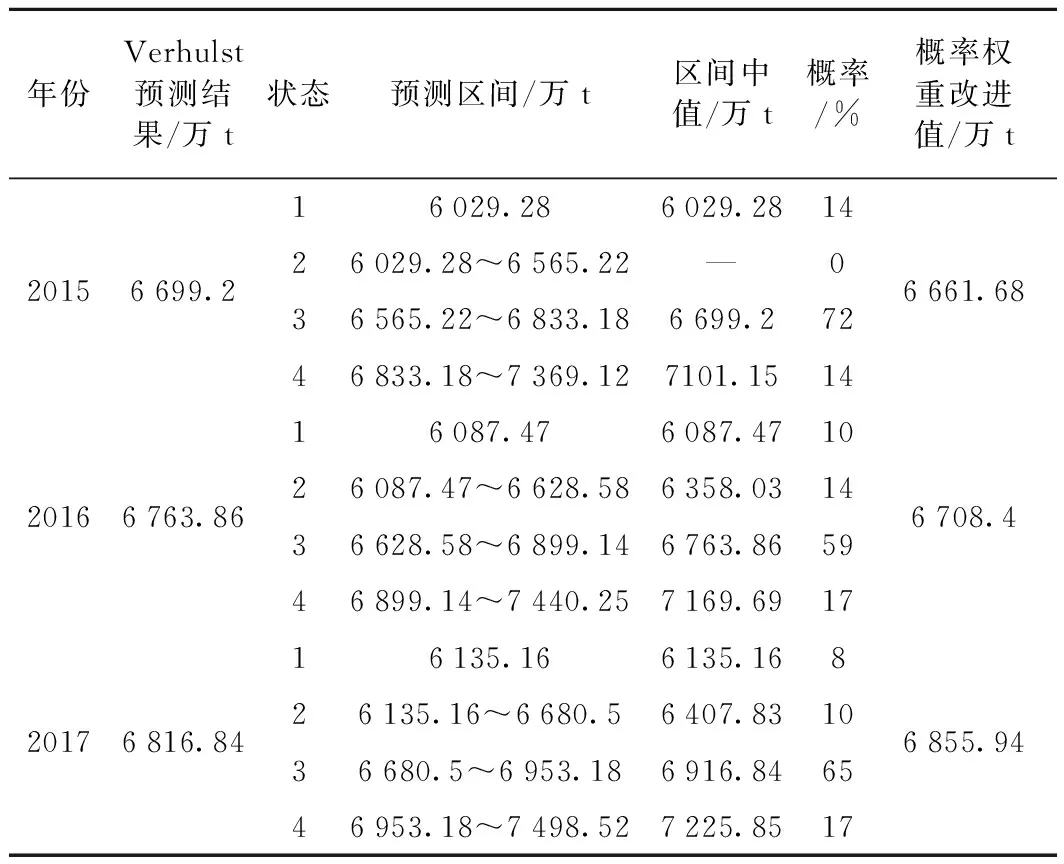
表6 馬爾科夫鏈改進后的貨運量預測值(2015~2017)
4 結論
(1)根據灰色Verhulst模型具有樣本數據需求量小,計算難度較低,預測精度較高,可預測原始數列呈現S增長的特點,對甘肅省2003~2014年鐵路貨運量數據進行擬合,構建灰色Verhulst模型預測。
(2)運用馬爾科夫鏈模型構造狀態轉移矩陣,可將預測數據按概率分布改進,從而再次提高其精度。
(3)通過實例分析驗證,選用馬爾科夫鏈改進的灰色Verhulst模型可用于甘肅省鐵路貨運量的預測。
(4)考慮到各種預測模型的適應性及優越性,合理構造多種模型組合的方法能夠有效地提高預測精度。在后續研究中不斷探索,創建精度更高的組合模型。
[1]耿立艷,張天偉,趙鵬.基于灰色關聯分析的LS-SVM鐵路貨運量預測[J].鐵道學報,2012,34(3):1-6.
[2]趙闖,劉凱,李電生.基于廣義回歸神經網絡的貨運量預測[J].鐵道學報,2004,26(1):12-15.
[3]劉志杰,季令,葉玉玲,等.基于徑向基神經網絡的鐵路貨運量預測[J].鐵道學報,2006,28(5):1-5.
[4]吳華穩.混沌時間序列分析及在鐵路貨運量預測中的應用研究[D].北京:中國鐵道科學研究院,2014.
[5]Aihara K,Takabe T,Toyoda M.Chaotic neural networks [J].Physics Letters A,1990,144(627):333-340.
[6]Suykens J A K,Vandewalle J.Learning a simple Recurrent neural state space model to behave like Chua’s double scroll[J].IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications,1995,42(8):499-502.
[7]Porporato A,Ridolti L.Multivariate nonlinear prediction of river flows[J].Journal of Hydrology,2001,248:109-122.
[8]D.R.Kulkarni,J.C.Parikh.Dynamic Predictions From Time Series Data-An Artificial Neural Network Approach[J].International Journal of Modern Physics C,1997,8(6):1345-1360.
[9]安永娥,鮑學英,王起才.基于無偏灰色Verhulst模型的鐵路貨運量預測研究[J].鐵道科學與工程學報,2016,13(1):181-186.
[10]戴文戰,熊偉,楊愛萍.灰色Verhulst模型的改進及其應用[J].化工學報,2010,61(8):2097-2100.
[11]楊琦,楊云峰,馮忠祥,等.基于灰色理論和馬爾科夫模型的城市公交客運量預測方法[J].中國公路學報,2013,26(6):169-174.
[12]林曉言,陳有孝.基于灰色-馬爾科夫鏈改進方法的鐵路貨運量預測研究[J].鐵道學報,2005,27(3):15-19.
[13]張誠,周湘峰.基于灰色預測-馬爾可夫鏈-定性分析的鐵路貨運量預測[J].鐵道學報,2007,29(5):15-21.
[14]曹飛.基于灰色殘差GM(1,1)模型的中國鐵路貨運量預測[J].北方經貿,2012(7):107-108.
[15]賈金平,吉莉.基于灰色加權馬爾可夫鏈的大連鐵路客運量預測[J].大連交通大學學報,2015,36(3):6-8.
Research on Railway Freight Volume Prediction Based on Markov Verhulst Model
YUAN Sheng-qiang,BAO Xue-ying,WANG Qi-cai
(School of Civil Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China)
Railway freight volume is one of the leading indicators of economic development in an area and accurate prediction of railway freight volume may serve as guidance to the development planning of this area.This paper is focused on the model error of the traditional grey Verhulst model used in railway freight volume forecasting to improve its prediction accuracy.Markov Chain model is used to modify and improve traditional Verhulst model.In the end,practical cases are introduced to verify the significance of Markov Chain to improve the prediction accuracy of the gray verhulst model,which is proved suitable for Gansu railway freight volume forecast.Therefore,the application of this model to predict the railway freight volume in Gansu province from 2015 to 2017 provides reliable indicators for the development of logistics,transportation and other related industries in the region.
Logistics and transportation; Railway freight volume; Verhulst model; Markov chain model; Prediction
2016-03-21;
2016-04-08
長江學者和創新團隊發展計劃滾動支持(IRT15R29)
袁勝強(1987—),男,碩士研究生。
鮑學英(1974—),女,教授,從事鐵路運輸管理及決策研究,E-mail:813257032@qq.com。
1004-2954(2016)10-0027-04
U294.1
A
10.13238/j.issn.1004-2954.2016.10.007

