多量測向量模型下基于貝葉斯檢驗的快速OMP算法研究

李少東 陳文峰 楊 軍 馬曉巖

?

多量測向量模型下基于貝葉斯檢驗的快速OMP算法研究

李少東*陳文峰 楊 軍 馬曉巖

(空軍預警學院三系 武漢 430019)

目前多量測向量(Multiple Measurement Vectors, MMV)模型的稀疏重構算法存在兩個問題：計算復雜度高和當重構的支撐集存在冗余時無法有效剔除。為同時提高MMV模型的重構效率和重構精度，該文提出一種MMV模型下基于貝葉斯檢驗的快速正交匹配追蹤(Fast Orthogonal Matching Pursuit based on Bayesian Testing, FOMP-BT)算法。首先，通過新原子組選和warm start求逆的思想來減少算法總的迭代次數以及每次迭代的運算量，以提高算法的重構效率；其次，利用貝葉斯檢驗的思想剔除冗余支撐集以提高重構精度；最后對所研究的算法從參數選擇以及計算復雜度等方面進行了理論分析。仿真結果表明，所提算法具有重構精度高、速度快以及對噪聲有較好的魯棒性等優勢。

多量測向量模型；快速正交匹配追蹤算法；迭代次數；貝葉斯檢驗

1 引言

作為一種信息獲取的新思路，壓縮感知(Compressive Sensing, CS)[1]自提出至今，理論日趨完善[2]。由于CS將采樣端的壓力“轉移”到解碼端，因此壓縮量測條件下的稀疏重構是CS的關鍵研究問題之一。多量測向量(Multiple Measurement Vector, MMV)問題作為CS的一個延伸發展方向，也引起了眾多學者的關注[3,4]。MMV模型是指不同矢量之間具有相同支撐集結構(對稀疏值的幅度不加約束)的模型，而對這種聯合稀疏特征的利用可提高重構精度、縮短重構時間[5]。因此，在生物特征識別[6]、圖像處理[7]、到達角估計[8]、空時自適應處理[9]以及雷達成像[10,11]等領域，眾多學者找到并構建了共享支撐集的MMV模型，取得了比單量測向量(Single Measurement Vector, SMV)模型更好的稀疏重構效果和抗噪性能。文獻[12]從信息論的角度揭示了MMV問題中支撐集恢復性能的邊界條件，奠定了使用MMV模型可改善重構性能的理論基礎。因此研究壓縮量測數據條件下對MMV問題的稀疏重構具有重要意義。

文獻[13]對較早時期MMV問題的重構算法進行了綜述與分析，并指出了每種算法的優缺點，給出了CS-MMV模型的發展趨勢。而近幾年求解MMV問題的稀疏重構算法主要分為兩大類：一是基于貪婪思想的重構方法，文獻[14]將DOA估計建模為MMV模型，基于導向矢量構成的冗余字典高度相關這一事實，對OMPMMV算法[4]進行了改進，使新算法可在冗余字典相關的條件下重構，但是并未考慮算法的快速實現問題；文獻[15]將5種典型重構SMV問題的算法拓展為求解MMV問題的算法，利用漸近RIP性質，推導了5種算法最優稀疏表示的充分條件，但是該文并未討論噪聲影響時的重構精度問題。總結此類算法可知，將貪婪算法思想拓展到求解MMV問題后，雖然在重構性能上比SMV條件下有所改善，但是貪婪算法固有的低信噪比下重構精度低、求逆運算量大的問題并未得到有效解決；二是基于稀疏貝葉斯學習(Sparse Bayesian Learning, SBL)理論的重構算法研究，文獻[16]利用子空間罰函數對MSBL進行改進，精度得到了提高；文獻[17]在進行DOA估計時，考慮了網格失配的問題，將聯合稀疏模型轉換為塊稀疏表示后，提出了OGBSBL算法，可在網格失配時獲得更好的DOA估計精度。但是此類算法受SBL的計算量影響，計算效率一直是值得進一步研究的問題。總結目前的研究成果可知，雖然有很多針對MMV問題的重構算法，但如何更好地利用聯合稀疏這一結構先驗信息，并從CS獲得的壓縮量測數據中快速魯棒地重構MMV問題依然值得進一步研究。

針對上述問題，本文提出了一種MMV模型下基于貝葉斯檢驗的快速正交匹配追蹤(Fast Orthogonal Matching Pursuit based on Bayesian Testing, FOMP-BT)算法。該算法主要的創新體現在兩個方面：重構效率和估計精度。首先，在提高算法的重構效率方面采用了兩種策略，一是減少算法總的迭代次數，即在每次迭代選擇新原子時，采用選擇一組原子(原子是指感知矩陣的某一列)代替原OMPMMV算法[4]每次只選擇一個原子的選擇機制以減少總的迭代次數；二是降低每次迭代的計算量，由于重構矩陣(由各次迭代獲得的原子合成的矩陣)每次迭代只增加一少部分的新原子，因此可采用“warm start”[18]的方式，充分利用前一次迭代獲得的重構原子信息，通過遞歸方法實現重構矩陣的求逆運算，從而降低求逆運算量；其次，在提高估計精度方面主要通過提高支撐集估計精度來實現，即利用貝葉斯檢驗的思想剔除冗余支撐集。最后，對所研究的算法從參數選擇、計算復雜性等方面進行了理論分析。此外，本文還構建了基于貪婪類算法的多向量重構算法的統一框架。將本文算法應用到圖像處理以及到達角估計等場合，具有較廣泛的應用前景。

2 MMV壓縮量測信號模型

首先對MMV問題進行建模，噪聲條件下MMV模型可表示為

文獻[3]對MMV模型的稀疏結構進行了詳細的說明，本文引用其假設條件，描述如下：

上述構建的模型又稱之為聯合稀疏模型。MMV模型對稀疏點的約束是其支撐集位置不隨列發生變化。為使模型更加合理，假設每一列的非零稀疏點幅度服從常用的伯努利高斯(Bernoulli Gauss, BG)模型。這里對MMV BG模型進行簡單介紹，為下文的支撐集貝葉斯檢驗奠定基礎。

在對模型稀疏點取非零值的概率和大小約束之后，下一步就是對其進行位置約束，為體現隨機性，本文假設信號非零行的位置是隨機的。至此，完成了壓縮MMV模型構建，下面針對此模型進行重構算法介紹。

3 FOMP-BT算法

>3.1 算法基本思想

由文獻[15]可知，求解MMV問題的貪婪類算法可由SMV的算法拓展得到，因此求解MMV問題的算法基本迭代格式是與SMV條件下一致的[15]。本文所提的FOMP-BT算法則是在OMPMMV算法[4]的基礎上，對重構效率和估計精度兩個方面進行改進，其算法流程如表1所示。

表1 FOMP-BT算法

從表1可以看出FOMP-BT算法的基本思想包括多原子識別、遞歸投影以及殘差更新3個步驟，其中迭代項為主要的計算量來源。而FOMP-BT算法對運算量的改進體現在前兩個步驟上，即多原子識別減少總的迭代次數，遞歸投影降低每次迭代求逆的運算量。此外FOMP-BT算法通過貝葉斯檢驗剔除冗余支撐集來減小誤差。下面重點對FOMP- BT的具體實現進行詳細分析。

3.2 算法實現步驟

首先分析如何降低算法的運算量，以第次迭代為例說明問題。

完成新重構原子組選后，便需要進行投影計算。令第次迭代得到的重構矩陣為，那么有，其中為第次迭代得到的重構矩陣，重構矩陣包含兩部分：一是前次迭代得到的；二是本次迭代時得到的新重構原子組。進行投影計算時，有

利用分塊求逆引理[18]，將式(5)的計算等價轉換為

相同的遞歸策略可以一直延續到算法迭代結束。至此，完成了對算法降低運算量部分的介紹，下面分析如何提高新算法的噪聲魯棒性。

同理依據貝葉斯公式以及式(10)，式(12)，可求得

得到參數的估計值后，需要進一步推導MMV模型下的非零行貝葉斯檢驗模型。

MMV條件下，當非零行數有冗余時，為正確識別真實的非零行數(剔除虛假冗余項)，本文采取貝葉斯模型對非零行進行檢驗。實際上，假設的其他非零行是已知，而檢驗的第行時，即對的檢驗對應式(16)所示事件：

令

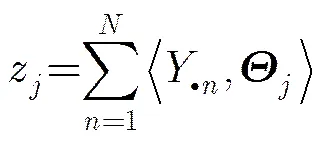
那么有

那么有

對式(22)取對數并化簡，可得到：

至此即完成對支撐集的檢驗。依次對所有的粗支撐集進行檢驗后可得到最終的檢驗結果。

從FOMP-BT算法的推導過程中可以看出，該算法在沿襲貪婪類算法的基本迭代框架(新原子識別、投影和殘差更新)基礎上，從降低運算量和提高精度的角度進行了創新。

3.3 參數設置

FOMP-BT算法待確定的參數主要有兩個：迭代停止條件與稀疏度預置值。下面對其選擇原則進行分析。

(1)迭代停止條件的選擇：目前關于貪婪類算法的迭代停止條件主要有兩種類型，一是在稀疏度已知條件下，迭代次。由于稀疏度先驗在實際情況中不易獲得，因而產生了稀疏度預估的思想，即利用量測長度、信號維度、稀疏度的關系預置稀疏度。文獻[21]提出了自適應稀疏度估計的思想，但其將稀疏度的先驗轉換為RIC常數的先驗，實際中RIC常數往往也是未知的。所以本文認為稀疏度自適應的重點應落腳于怎么將一個不合理的甚至是冗余的稀疏度經過算法處理之后逼近真實稀疏度。

第2種典型是利用殘差作為迭代停止條件。即在估計過程當中，殘差是逐步變小的，當殘差變大時，說明估計已經充分，剩余的為噪聲估計，因而出現變大的情況。此時需要噪聲的方差作為先驗，但是由于方差估計一般會存在誤差，因此也會造成最終的支撐集出現冗余。

4 算法性能分析

本文降低運算量和提高精度的思想適用于貪婪類的大部分算法，圖1為MMV模型下貪婪類算法的統一框架。從圖1可以看出，本文思想適用于識別和投影處理，具有較強的可移植性。

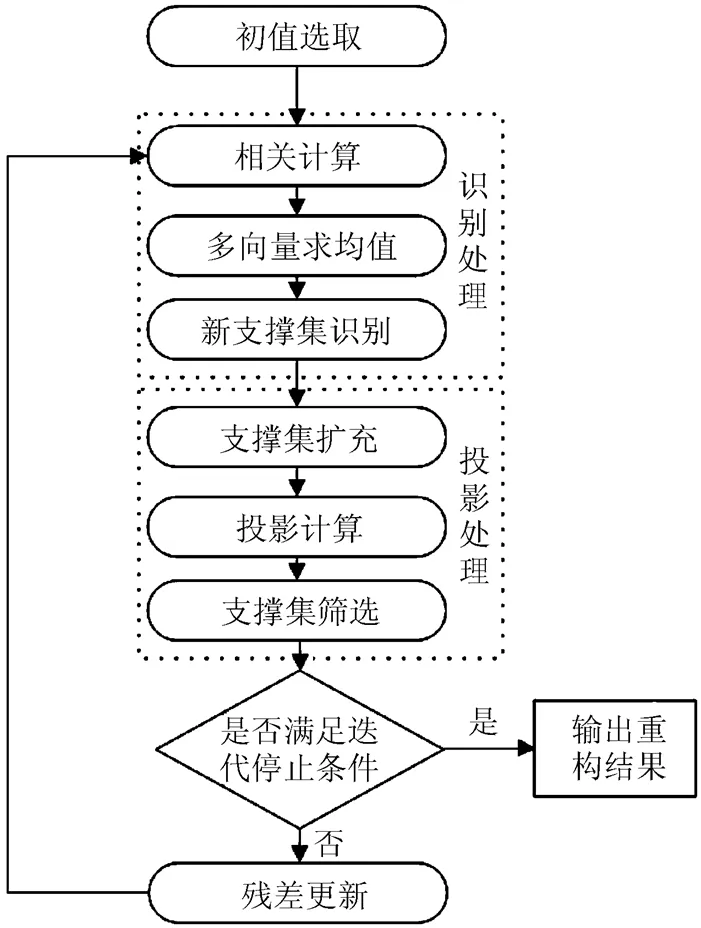
圖1 基于貪婪類算法的MMV算法統一描述框圖

此外，通過定量分析FOMP-BT算法的計算量來體現其優勢，下面分別從識別步和投影步出發，計算第次循環時算法的運算量。以一次乘法或者是加法的運算量為一個運算量單位，重點對比FOMP-BT算法與OMPMMV算法的計算量。首先計算FOMP-BT計算量。

在FOMP-BT算法中，主要計算量集中于新原子識別步和投影步。而一次迭代中新原子識別步的計算量為。在投影步時計算量主要集中于的計算。的維度是，因此對其求逆的計算量為。維度是，其計算量為，假設經過次迭代，那么算法總運算量約為

其次計算OMPMMV算法的計算量。

OMPMMV算法的主要計算量同樣是集中于新原子識別步和投影步。由于不存在快速操作，假設一共迭代0次，其總的計算量約為

5 仿真與分析

首先對噪聲添加方式和重構質量指標進行說明。信噪比定義為

其次，本文使用相對重構誤差來衡量重構質量，其定義為

仿真1 冗余稀疏度對重構結果的影響 為比較冗余稀疏度對重構結果的影響，仿真參數設置如下：測量值=300，信號維度為=500，真實稀疏度=12(即MMV模型有12個非零行)，向量數為10，每一列向量非零值的幅度服從方差為1的高斯分布。蒙特卡羅次數為100，信噪比為3 dB。冗余稀疏度從15增加到42，步長為3。分別與OMPMMV[4]以及SCoSaMP[15]算法作對比，圖2為仿真結果。

夫妻之間關系非常糟糕，因為妻子長期積怨而常年爭吵不休。起因是結婚前，妻子聽說她丈夫有十畝地和一份收入頗豐的工作。丈夫因妻子生了女兒而不是兒子十分生氣，所以他照顧妻子時態度惡劣。

圖2 不同算法重構誤差對比

從圖2對比可以看出，隨著冗余稀疏度變大，3種算法的誤差都相應增大，CoSaMP算法由于每次迭代時都選擇稀疏度的2倍個支撐集原子，因此當稀疏度存在冗余時，其錯誤重構的概率大于OMPMMV，性能劣于OMPMMV算法；而本文算法采用了貝葉斯檢驗剔除冗余支撐集，因此在相同的稀疏度條件下，重構誤差最小。從真實稀疏度為6和為12時算法誤差對比可以看出，當余稀疏度越大，本文剔除虛假支撐的能力越強。仿真驗證了本文算法對冗余稀疏度剔除的有效性。

仿真2 抗噪性能對比 為考察噪聲對算法精度的影響，將算法停止條件變為，仿真時取輸入信噪比為3~18 dB，其他條件與仿真1相同，仿真時分別與MFOCUSS[3], OMPMMV[4]以及CoSaMP[15]算法進行對比，結果如圖3所示。

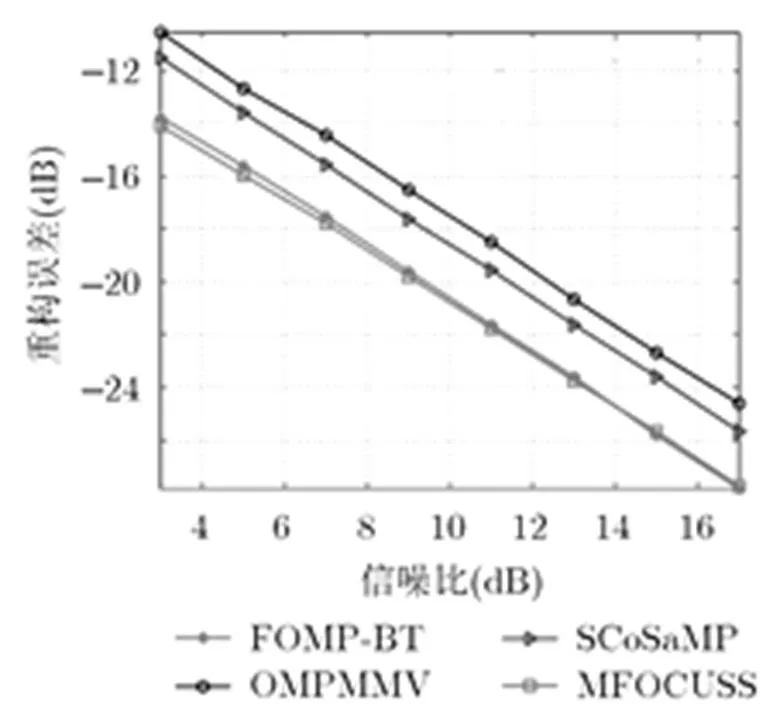
圖3 不同信噪比條件下的重構精度對比

從圖3中可以看出，隨著信噪比的提高，各類算法的重構誤差呈現遞減趨勢。從總體趨勢看，本文算法受噪聲影響與MFOCUSS基本相同。說明本文算法在經過支撐集剔除步驟之后，用于重構的支撐集最接近于信號的真實支撐集，參與最終重構的支撐集中包含的虛假成分最少，因而精度較高；而其他算法在重構時受到噪聲的影響，會存在冗余的稀疏度，因此影響了算法在噪聲條件下重構的精度。仿真驗證了本文算法在低信噪比條件下依然具有較好的重構能力。

仿真3 不同算法重構效率對比 本仿真主要用于對比不同算法的運行效率。仿真參數設置如下：取信號維度為變量，范圍是500~900，步長為50，量測值個數取為信號維度的0.6倍，即，信噪比為3 dB，蒙特卡洛次數為100，分別計算FOMP-BT, OMPMMV, SCoSaMP與MFOCUSS算法的運行時間，結果如圖4所示。

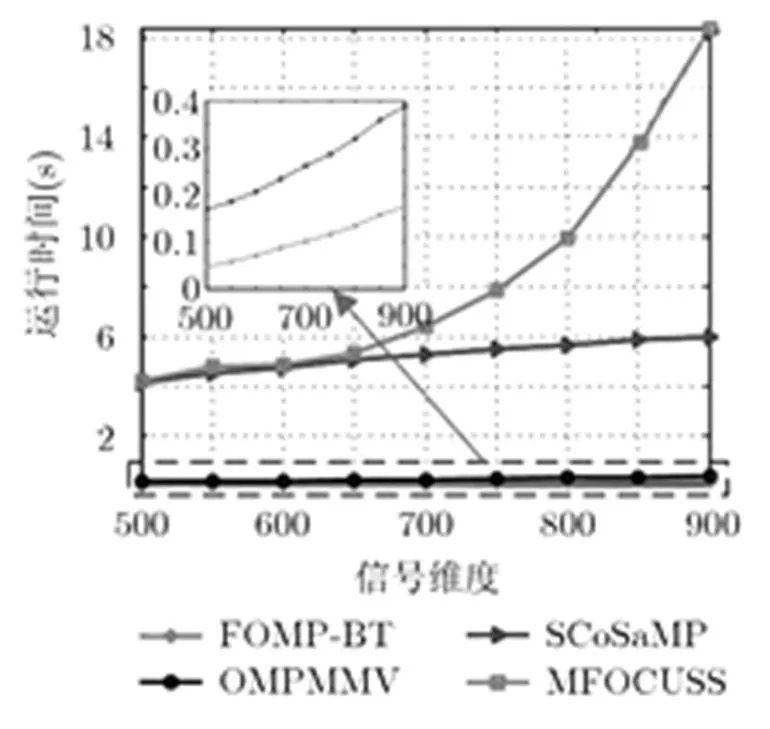
圖4 不同算法的運行時間比較

從圖4可以看出，由于MFOCUSS算法存在大矩陣求逆運算，隨著信號維度的增加其運行時間增加的最快；SCoSaMP算法由于每次迭代時都需要對個原子的重構矩陣進行求逆運算，因此其計算量高于OMPMMV和FOMP-BT；本文算法由于采取了減少迭代次數和優化每次迭代時逆矩陣的運算量，因此運算時間最短。仿真驗證了本文算法的高重構效率優勢。

6 結束語

MMV模型能夠提供更多的先驗信息，對此信息的利用可用于提高重構概率。本文針對目前求解MMV問題的算法復雜度高以及低信噪比條件下存在冗余支撐集的問題，提出了FOMP-BT算法，該算法的主要優勢在于兩個方面：(1)通過減少算法總的迭代次數和降低每次迭代的運算量的方式，使得算法的重構效率有了較大的提高；(2)利用貝葉斯檢驗的思想，可剔除冗余支撐集，由于剔冗的支撐集更加接近真實支撐集結構，因此可提高重構精度。在實際應用時，需要結合背景，尋找恰當的MMV模型場合。將本文算法應用到ISAR/SAR的距離向聯合成像是課題組下一步工作的研究重點。

[1] DONOHO D L. Compressed sensing[J]., 2006, 52(4): 1289-1306.

[2] ELDAR Y C. Sampling Theory Beyond Band Limited Systems[M]. Cambridge University Press, 2015: 1-8. doi: http: //dx.doi.org/10.1017/CBO9780511762321.

[3] SHANE F C, BHASKAR D R, KJERSTI E,Sparse solutions to linear inverse problems with multiple measurement vectors[J]., 2005, 53(7): 2477-2488.

[4] CHEN Jie and HUO Xiaoming. Theoretical results on sparse representations of multiple-measurement vectors[J]., 2006, 54(12): 4634-4643.

[5] 陳一暢, 張群, 陳校平, 等. 多重測量矢量模型下的稀疏步進頻率SAR成像算法[J]. 電子與信息學報, 2014, 36(12): 2987-2993. doi: 10.3724/SP.J.1146.2013.01831.

CHEN Yichang, ZHANG Qun, CHEN Xiaoping,Imaging algorithm of sparse stepped fequency SAR based on multiple measurement vectors model[J].&, 2014, 36(12): 2987-2993. doi: 10.3724/SP.J.1146.2013.01831.

[6] HEKHAR S, PATEL V M, NASRABADI N M ,. Joint sparse representation for robust multimodal biometrics recognition[J]., 2014, 36(1): 113-126.

[7] 李志林, 陳后金, 李居朋, 等. 一種有效的壓縮感知圖像重建算法[J]. 電子學報, 2011, 39(12): 2796-2800.

LI Zhilin, CHEN Houjin, LI Jupeng,. An eficient algorithm for compressed sensing image reconstruction[J]., 2011, 39(12): 2796-2800.

[8] ZHAO Tan and NEHORAI A. Sparse direction of arrival estimation using co-prime arrays with off-grid targets[J]., 2014, 21(1): 26-29.

[9] 王澤濤, 段克清, 謝文沖, 等. 基于SA-MUSIC 理論的聯合稀疏恢復STAP算法[J]. 電子學報, 2015, 43(5): 846-853.

WANG Zetao, DUAN Keqing, XIE Wenchong,. A joint sparse recovery STAP method based on SA-MUSIC[J]., 2015, 43(5): 846-853.

[10] FANG Jian, XU Zongben, ZHANG Bingchen,. Compressed sensing SAR imaging with multilook processing [OL]. http://arxiv.org/abs/1310.7217v1, 2013.

[11] TAO Yu, ZHANG Gong, and ZHANG Jindong. Guaranteed stability of sparse recovery in distributed compressive sensing MIMO Radar[J]., 2015, Article ID 421740: 1-10.

[12] JIN Yuzhe and RAO B D. Support recovery of sparse signals in the presence of multiple measurement vectors[J]., 2013, 59(5): 3139-3156.

[13] 王法松, 張林讓, 周宇. 壓縮感知的多重測量向量模型與算法分析[J]. 信號處理, 2012, 28(6): 785-792.

WANG Fasong, ZHANG Linrang, and ZHOU Yu. Multiple measurement vectors for compressed sensing: model and algorithms analysis[J]., 2012, 28(6): 785-792.

[14] GUAN Gui, WAN Qun, and ADACHI F. Direction of arrival estimation using modified orthogonal matching pursuit algorithm[J]., 2011, 6(22): 5230-5234.

[15] BLANCHARD J D, CERMAK M, HANLE D,. Greedy algorithms for joint sparse recovery[J]., 2014, 62(7): 1694-1704.

[16] YE J C, KIM J M, and BRESLER Y. Improving M-SBL for joint sparse recovery using a subspace penalty[OL]. http:// arxiv:1503.06679v1, 2015.

[17] ZHANG Y, YE Z F, XU X,. Off-grid DOA estimation using array covariance matrix and block-sparse Bayesian learning[J]., 2014, 98: 97-201.

[18] 張賢達. 矩陣分析與應用(第2版)[M]. 北京: 清華大學出版社, 2013: 54-64.

ZHANG Xianda. Matrix Analysis and Applications (Second Edition)[M]. Beijing: Tsinghua University Press, 2013: 54-64.

[19] ZHANG Jingxiong and YANG Ke. Informational analysis for compressive sampling in radar imaging[J].2015, 15(4): 7136-7155. doi: 10.3390/s150407136.

[20] 甘偉, 許錄平, 蘇哲, 等. 基于貝葉斯假設檢驗的壓縮感知重構[J]. 電子與信息學報, 2011, 33(11): 2640-2646. doi: 10. 3727/SP.J.1146.2011.00151.

GAN Wei, XU Luping, SU Zhe ,. Bayesian hypothesis testing based recovery for compressed sensing[J].&, 2011,33(11): 2640-2646. doi: 10.3727/SP.J.1146.2011.00151.

[21] 楊成, 馮巍, 馮輝, 等. 一種壓縮采樣中的稀疏度自適應子空間追蹤算法[J]. 電子學報, 2010, 38(8): 1914-1917.

YANG Cheng, FENG Wei, FENG Hui,. A sparsity adaptive subspace pursuit algorithm for compressive sampling[J]., 2010, 38(8): 1914-1917.

Fast OMP Algorithm Based on Bayesian Test for Multiple Measurement Vectors Model

LI Shaodong CHEN Wenfeng YANG Jun MA Xiaoyan

(,430019,)

There are two issues in the Sparse Reconstruction (SR) algorithm of Multiple Measurement Vectors (MMV). One is the high computation complexity and the other is that redundant support set can not be effectively removed. In order to improve the efficiency and accuracy of SR algorithm simultaneously for MMV model, a Fast Orthogonal Matching Pursuit algorithm based on Bayesian Test (FOMP-BT) is presented in this paper. Firstly, the total number of iterations and the computation of each iteration are reduced through the new atomic group selection and warm start matrix inversion, thus the efficiency of the algorithm is improved. Secondly, using the idea of the Bayesian test to eliminate redundant support set, the accuracy of reconstruction is improved. Finally, the theoretical analysis of the algorithm is carried out from the aspects of parameter selection and computation complexity. The simulation results show that the proposed algorithm has the advantages of high accuracy, fast speed and good robustness to noise.

Multiple measurement vectors model; Fast Orthogonal Matching Pursuit (FOMP) algorithm; Number of iterations; Bayesian test

TN957.52

A

1009-5896(2016)07-1731-07

10.11999/JEIT151131

2015-10-10；改回日期：2016-02-25；網絡出版：2016-04-07

李少東 liying198798@126.com

李少東： 男，1987年生，博士，研究方向為壓縮感知理論在雷達成像中的應用.

陳文峰： 男，1989年生，博士，研究方向為雷達目標檢測與識別.

楊 軍： 男，1973年生，副教授，碩士生導師，研究方向為雷達目標檢測、現代信號處理.

馬曉巖： 男，1962年生，教授，博士生導師，研究方向為雷達目標檢測與識別.