知識庫中的信息測度

黃衛華

（文山學院 數學學院，云南 文山 663099）

知識庫中的信息測度

黃衛華

（文山學院 數學學院，云南 文山 663099）

在粗糙集理論中，基于度量決策表中屬性重要性大小的需要，有學者提出了互補信息熵的概念。在此基礎上，定義了條件熵和互信息等概念，并驗證了三者之間的關系，即互補信息熵是條件熵與互信息的和；類似于互補信息熵，互信息同樣具有單調性。

信息測度；互補信息熵； 條件熵；互信息

1948年美國數學家ShannonC.E在《貝爾系統技術》雜志上發表了一篇“通信的數學理論”的論文，該論文的發表標志一門新的學科──信息論的誕生。在這篇論文中，Shannon定義了信息熵，給出了關于信息系統實際結構的不確定性度量，并成功應用于許多不同的研究領域。一些學者利用Shannon熵的定義以及Shannon熵的變式度量了粗糙集理論的不確定性[1-7]。梁吉業[8]等定義了粗糙集理論的互補信息熵，并驗證該信息熵具有單調性，本文在此基礎上定義了條件熵和互信息，給出了三者之間的關系。

1　預備知識

定義1[9]設K=(U, R)是一個近似空間，U是一個非空有限論域，R是U上的一個等價關系，U/R={X1, X2…Xm}表示R的所有等價類構成的集合，[x]R表示包含元素x∈U的R等價類。特別地，U的劃分(U)={{x}|x∈U}稱為恒等關系，劃分?(U)={U}稱為全域關系。一個近似空間K=(U, R)可以看作是一個關于U的知識庫。

定義2[9]給定知識庫K=(U, R)，對于每一個KU，一個等價關系R，定義兩個子集

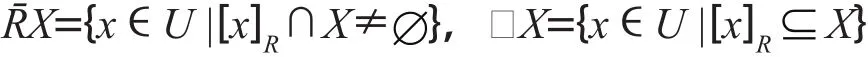
分別稱它們為X的R上近似集和R下近似集。

定義3[10]設K=(U, R)是一個近似空間，P, Q是U的兩個劃分，U/P={P1, P2…, Pm}，U/Q={Q1, Q2…, Qn},如果對于任意的Xi∈U/P，均有Yj∈U/Q，使得XiYj，稱U/P是U/Q的加細，記作U/PU/Q。

定義4[8]設K=(U, R)是一個近似空間，U是一個非空有限論域，U/R={X1, X2…Xm}是U上的一個等價關系，粗糙集的互補信息熵定義為

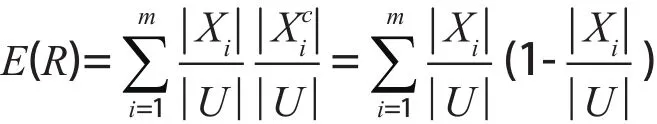
定義5設U是一個非空有限論域，K1=(U, P)和K2=(U, Q)是關于U的兩個知識庫，其中U/P={P1, P2, …, Pm}，U/Q={Q1, Q, …, Qn}，Q關于P的條件熵E(Q/P)定義如下

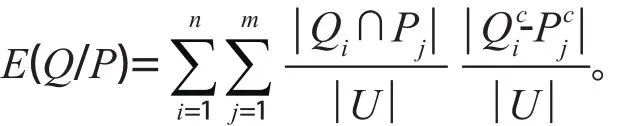
定義6設U是一個非空有限論域，K1=(U, P)和K2=(U, Q)是關于U的兩個知識庫，其中U/P={P1, P2, …, Pm}，U/Q={Q1, Q, …, Qn}，Q和P的互信息E(Q; P)定義如下

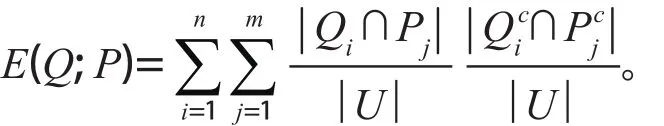
2　主要結論

定理1設U是一個非空有限論域，K1=(U, P)和K2=(U, Q)是關于U的兩個知識庫，那么E(Q; P)=E(Q)-E(Q/P)。

證明：設U/P={P1, P2, …, Pm}，U/Q={Q1, Q, …, Qn}，由集合論知，所以

所以E(Q; P)=E(Q)-E(Q/P)。

定理2設U是一個非空有限論域，K1=(U, P)和K2=(U, Q)是關于U的兩個知識庫，D是U的決策屬性集，如果U/PU/Q，那么E(D; P)≥E(D; Q)。

證明：設U/P={P1, P2, …, Pm}，U/Q={Q1, Q2, …, Qn}，U/D={d1, d2, …, dr}。因為U/PU/Q，所以m>n且存在集合{1, 2, …, m}的一個劃分C={C1, C2, …, Cn}，滿足因此

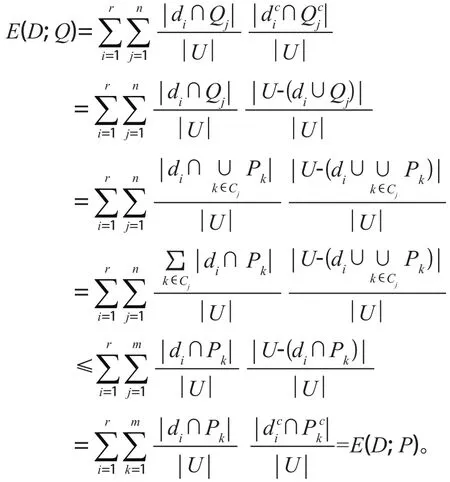
定理2表明隨著劃分的加細，信息粒度的互信息單調增加。定理2的逆命題一般情況下不成立。

例1設U={1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }，U/Q={{1, 5}{2, 3, 4, 6, 7}{8, 9, 10 }}，U/P={{1, 3, 4}{2, 5, 6}{7, 8, 9, 10 }}，U/D={{1, 3, 5, 8, 9}{2, 4, 6, 7, 10 }}。

計算

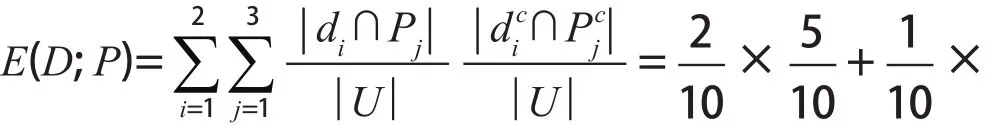
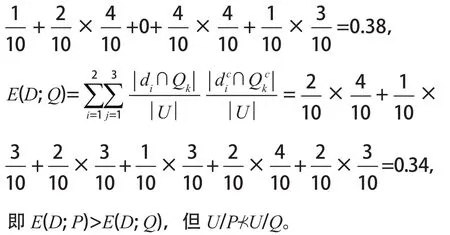
定理3設U是一個非空有限論域，K1=(U, P)和K2=(U, Q)是關于U的兩個知識庫，則U/PU/Q成立的充要條件是E(Q/P)=0。

證明：設U/P={P1, P2, …, Pm}，U/Q={Q1, Q2, …, Qn}。

3　結論

[1] Shannon C E. The mathematical theory of communication[J]. Bell Syst Technol J, 1948(3, 4): 373-423, 623-656.

[2] Beaubouef, T., Petry, F.E. and Arora, G. Information-theoretic measures of uncertainty for rough sets and rough relational databases[J]. Information Sciences, 1998 (59)：185-195.

[3] De Luca, A. and Termini, S. A definition of a nonprobabilistic entropy in the setting of fuzzy theory[J].Information and Control,1972(6):301-312.

[4] Liang, J.Y., Xu, Z.B. Uncertainty measures of roughness of knowledge and rough sets in incomplete information systems[C]//Proceedings of the 3rd World Congress on Intelligent Control and Automation (Press of University of Science and Technology of China, Hefei)，2000(2)：2526-2529.

[5] Liang, J.Y., Xu, Z.B. and Miao, D.Q. Reduction of knowledge in incomplete information systems[C]//Proceedings of Conference on Intelligent Information Processing in 16th World Computer Congress (Publishing House of Electronics Industry, Beijing) ，2000(7)：528-532.

[6] Wierman, M.J.Measuring uncertainty in rough set theory[J]. International Journal of General Systems, 1999(4)：283-297.

[7] Düntsch, I. , Gediga, G. Uncertainty measures of rough set prediction[J].Artificial Intelligence，1998, 106：109-137.

[8] Liang J Y, Chin K S, Dang C Y, et al. A new method for measuring uncertainty and fuzziness in rough set theory[J].Int J Gen Syst, 2002(4)：331-342.

[9] 張文修，吳偉志，梁吉業，等.粗糙集理論與方法[M].北京：科學出版社，2001：151-152.

[10] Pawlak Z. Rough sets[J]. International Journal of Computer and Information Sciences, 1982(5)：341-356.

The Information Measure in Knowledge Library

HUANG Weihua
(School of Mathematics, Wenshan University, Wenshan Yunnan 663099, China)

The concept of complementary information entropy based on the needs of the importance of attributes in measuring decision table is proposed in rough set theory. On this basis, condition entropy and mutual information are defi ned and the relationship among the three is verifi ed, i.e. the sum of condition entropy and mutual information is complementary information entropy; Mutual information also has the monotonicity similar to complementary information entropy.

information measure; complementary information entropy; conditional entropy; mutual information

TP18

A

1674 - 9200（2016）03 - 0042 - 03

（責任編輯劉常福）

2016 - 03- 03

云南省教育廳科研基金項目“基于粗糙集的數據挖掘算法研究”（ 2015Y470 ）。

黃衛華，女，河南中牟人，文山學院數學學院講師，碩士，主要從事信息代數和粗糙集理論研究。