干氣密封的實(shí)際氣體焦耳-湯姆遜效應(yīng)分析

鄧成香，宋鵬云，馬愛(ài)琳

?

干氣密封的實(shí)際氣體焦耳-湯姆遜效應(yīng)分析

鄧成香，宋鵬云，馬愛(ài)琳

（昆明理工大學(xué)化學(xué)工程學(xué)院，云南 昆明 650500）

干氣密封系統(tǒng)中氣體通過(guò)過(guò)濾器、閥門(mén)、孔板和密封端面等組件時(shí)會(huì)發(fā)生焦耳-湯姆遜（JT）效應(yīng)，可能導(dǎo)致密封氣溫度降低，甚至出現(xiàn)液相凝析。焦耳-湯姆遜效應(yīng)一般通過(guò)焦耳-湯姆遜系數(shù)來(lái)反映。針對(duì)干氣密封常面臨的氫氣、氮?dú)狻⒖諝夂投趸迹肰DW方程、RK方程、SRK方程和PR方程4個(gè)經(jīng)典狀態(tài)方程（EOS）分別計(jì)算了相應(yīng)的焦耳-湯姆遜（JT）系數(shù)，并與文獻(xiàn)實(shí)驗(yàn)數(shù)據(jù)進(jìn)行了比較，選擇最佳狀態(tài)方程作出各氣體的JT系數(shù)曲線和焦耳-湯姆遜反轉(zhuǎn)曲線（JTIC），并利用編程計(jì)算出空氣和氮?dú)馔ㄟ^(guò)干氣密封端面時(shí)，由于JT效應(yīng)引起的氣體溫降。結(jié)果表明：實(shí)際氣體的焦耳-湯姆遜效應(yīng)，對(duì)干氣密封的節(jié)流環(huán)節(jié)會(huì)產(chǎn)生重要影響。常溫條件下，氫氣發(fā)生致熱效應(yīng)，而氮?dú)狻⒖諝夂投趸細(xì)怏w發(fā)生致冷效應(yīng)。采用4種狀態(tài)方程計(jì)算焦耳-湯姆遜系數(shù)時(shí)，RK方程的平均相對(duì)誤差和最大相對(duì)誤差最低且分別小于4%和10%。干氣密封氣體的實(shí)際氣體焦耳-湯姆遜效應(yīng)能引起較大的溫度變化，其中氣體介質(zhì)壓力比介質(zhì)溫度對(duì)溫差的影響更大。壓力較小時(shí)JT效應(yīng)引起的溫降可以忽略。

干氣密封；實(shí)際氣體；狀態(tài)方程；焦耳-湯姆遜系數(shù)；反轉(zhuǎn)曲線

引 言

實(shí)際氣體流動(dòng)過(guò)程，由于節(jié)流效應(yīng)，氣體發(fā)生絕熱不可逆膨脹導(dǎo)致溫度變化的現(xiàn)象稱為焦耳-湯姆遜效應(yīng)。氣體在膨脹后溫度降低，稱為冷效應(yīng)；溫度保持不變時(shí)稱為零效應(yīng)；溫度升高時(shí)稱為熱效應(yīng)。密封氣通過(guò)干氣密封系統(tǒng)中過(guò)濾器、閥門(mén)、孔板和密封端面等組件時(shí)一般會(huì)發(fā)生焦耳-湯姆遜冷效應(yīng)，導(dǎo)致密封氣溫度降低，并可能出現(xiàn)凝析現(xiàn) 象[1]。如果析出液體進(jìn)入干氣密封端面，就會(huì)改變干氣密封的工況條件，導(dǎo)致氣膜狀態(tài)和作用力發(fā)生改變，從而影響干氣密封的使用效果及使用壽命[2]，甚至導(dǎo)致密封失效等重大安全問(wèn)題。許靜等[3-4]利用求解雷諾方程和數(shù)值分析的方法對(duì)螺旋槽干氣密封進(jìn)行了研究，得出氣體熱黏效應(yīng)對(duì)干氣密封性能的影響。針對(duì)干氣密封的研究一般把氣體處理為理想氣體，但是隨著干氣密封性能研究的不斷深入，其應(yīng)用范圍從低速、常壓擴(kuò)大到高速、高壓，且在高壓工況下，氣體的行為與理想氣體有較大差異[5-6]。通過(guò)分析、評(píng)價(jià)密封氣的焦耳-湯姆遜效應(yīng)可以預(yù)先評(píng)估干氣密封系統(tǒng)的安全可靠性能，并可采取有效措施克服由于焦耳-湯姆遜效應(yīng)帶來(lái)的不利影響。但是，到目前為止，尚未發(fā)現(xiàn)對(duì)干氣密封封氣介質(zhì)的實(shí)際氣體焦耳-湯姆遜效應(yīng)的研究。

本文針對(duì)干氣密封常面臨的氫氣、氮?dú)狻⒖諝夂投趸迹治霾煌瑲怏w狀態(tài)方程用于求解焦耳-湯姆遜系數(shù)的準(zhǔn)確性，利用最佳狀態(tài)方程作出JT系數(shù)曲線和JT反轉(zhuǎn)曲線，并計(jì)算出干氣密封中JT效應(yīng)引起的空氣在不同介質(zhì)溫度和不同外部壓力時(shí)的溫差。

1 焦耳-湯姆遜（JT）系數(shù)

實(shí)際氣體在等焓節(jié)流過(guò)程中溫度隨壓力的變化速率，即溫熵圖（-）中的等焓線上任一點(diǎn)的斜率稱為焦耳-湯姆遜（JT）系數(shù)[7]。JT系數(shù)的準(zhǔn)確計(jì)算對(duì)評(píng)價(jià)實(shí)際氣體的焦耳-湯姆遜效應(yīng)至關(guān)重要。焦耳-湯姆遜系數(shù)表達(dá)式[8]為

其中

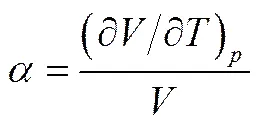
式中，JT為JT系數(shù)，K·MPa-1；為溫度，K；為壓力，MPa；為摩爾體積，m3·mol-1；為壓縮因子；為氣體常數(shù)，8.314 J·mol-1·K-1；,real為實(shí)際氣體的摩爾比定壓熱容，J·mol-1·K-1。

1.1 立方型狀態(tài)方程

氣體狀態(tài)方程可化為的三次展開(kāi)式，也可以根據(jù)化為的三次展開(kāi)式，稱為立方型狀態(tài)方程，其形式簡(jiǎn)單，方程中一般只有兩個(gè)常數(shù)，且常數(shù)可以通過(guò)純物質(zhì)臨界性質(zhì)和偏心因子計(jì)算。各氣體的臨界參數(shù)和偏心因子如表1所示。

表1 臨界參數(shù)和偏心因子[10]

4種經(jīng)典立方型狀態(tài)方程式如下[11]。

VDW:

(3)

RK:

(4)

SRK:

(5)

PR:

(6)

以上4種立方型方程式（3）～式（6）中的參數(shù)，如表2所示。

表2 4種立方型狀態(tài)方程的壓縮因子展開(kāi)式的參數(shù)[11]

對(duì)空氣可視為由摩爾分?jǐn)?shù)分別為0.7812和0.2188的氮和氧組成的二元混合氣體。立方型狀態(tài)方程中的參數(shù)和采用混合規(guī)則計(jì)算[12-14]

其中交叉項(xiàng)可按式（9）計(jì)算

式中，為氮?dú)獾哪柗謹(jǐn)?shù)；為氧氣的摩爾分?jǐn)?shù)；為氮?dú)馀c氧氣的二元交互作用參數(shù)。

1.2 壓縮因子

雖然對(duì)壓縮因子的研究比較豐富，有大量的實(shí)驗(yàn)數(shù)據(jù)和經(jīng)驗(yàn)公式，但通過(guò)理論方法計(jì)算壓縮因子的研究較少。本文用代入式（3）～式（6）得到狀態(tài)方程的壓縮因子三次展開(kāi)式如式（10）所示，其中參數(shù)如表2所示。

利用卡爾丹公式[15]可解得符合條件的壓縮因子值。

其中

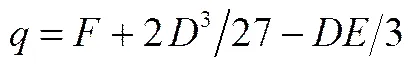
得到符合條件的壓縮因子值

1.3 實(shí)際氣體摩爾比定壓熱容

實(shí)際氣體的比定壓熱容,real既是溫度的函數(shù)，又是壓力的函數(shù)，它由理想氣體的比熱容（,ideal）和剩余比熱容（?c）兩部分組成[16]。本文采用VDW方程、RK方程、SRK方程和PR方程的剩余焓（R）推導(dǎo)出剩余比熱容（?）的計(jì)算公式。

聯(lián)立式（3）～式（6）和式（14）～式（16），即可得分別按照VDW方程、RK方程、SRK方程和PR方程推導(dǎo)出的剩余比熱容（）的計(jì)算公式分別如下所示。

VDW：

RK：

SRK：

PR：

計(jì)算理想氣體比定壓熱容公式[8]如式（21）所示，其中的參數(shù)見(jiàn)表3。

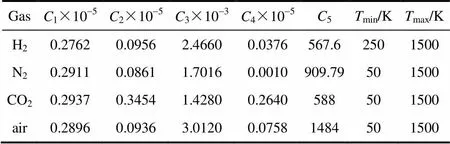
表3 理想氣體比定壓熱容的參數(shù)[10]

聯(lián)合式（2）、式（12）和式（13），可分別求得氮?dú)狻⒖諝夂投趸荚诓煌瑴囟群筒煌瑝毫ο碌腏T系數(shù)，按照VDW方程、RK方程、SRK方程和PR方程計(jì)算的JT系數(shù)，與文獻(xiàn)[10]的實(shí)驗(yàn)數(shù)據(jù)進(jìn)行比較，部分結(jié)果如表4～表6所示。實(shí)際計(jì)算了壓力分別等于0.1、1、2、6、10 MPa的數(shù)據(jù)，表4～表6示出了壓力等于0.1 MPa和壓力等于10 MPa的結(jié)果。各種壓力下JT系數(shù)計(jì)算結(jié)果與文獻(xiàn)實(shí)驗(yàn)結(jié)果的相對(duì)誤差如表7所示。由于目前為止，尚未發(fā)現(xiàn)有關(guān)氫氣的JT系數(shù)的實(shí)驗(yàn)數(shù)據(jù)，通過(guò)計(jì)算氮?dú)狻⒖諝夂投趸嫉腏T系數(shù)選擇最佳狀態(tài)方程，并認(rèn)為該狀態(tài)方程同樣適用于計(jì)算氫氣的JT系數(shù)。表中EXP表示來(lái)自文獻(xiàn)[10]的實(shí)驗(yàn)數(shù)據(jù)，VDW、RK、SRK和PR分別表示利用相應(yīng)方程求得的JT系數(shù)，RE表示相對(duì)誤差，AVE表示平均相對(duì)誤差，Min表示最小相對(duì)誤差，Max表示最大相對(duì)誤差。其中。

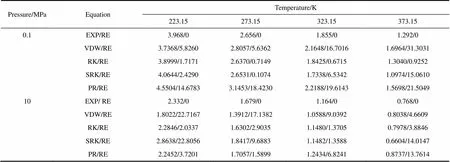
表4 不同溫度和不同壓力下氮?dú)獾腏T系數(shù)計(jì)算結(jié)果比較

Note: Results are (JT/K·MPa-1)/(RE/%).

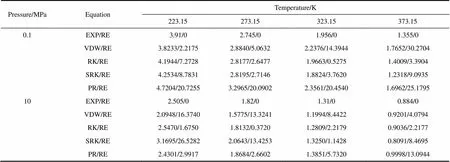
表5 不同溫度和不同壓力下空氣的JT系數(shù)計(jì)算結(jié)果比較

Note: Results are (JT/K·MPa-1)/(RE/%).

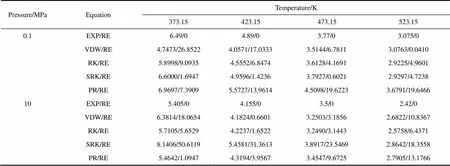
表6 不同溫度和不同壓力下二氧化碳的JT系數(shù)計(jì)算結(jié)果比較

Note: Results are (JT/K·MPa-1)/(RE/%).

通過(guò)利用VDW方程 、RK方程、SRK方程和PR方程分別計(jì)算氮?dú)狻⒖諝夂投趸嫉腏T系數(shù)與文獻(xiàn)[10]實(shí)驗(yàn)數(shù)據(jù)比較，其計(jì)算的平均相對(duì)誤差、最小相對(duì)誤差和最大相對(duì)誤差如表7所示。

表7 各種算法的相對(duì)誤差對(duì)比

從表7可以看出：通過(guò)4種狀態(tài)方程計(jì)算JT系數(shù)的誤差分析，RK方程平均相對(duì)誤差和最大相對(duì)誤差最低且分別小于4%和10%。4種狀態(tài)方程中，RK方程用于計(jì)算干氣密封氣的JT系數(shù)時(shí)，精度較高。

1.4 焦耳-湯姆遜（JT）系數(shù)曲線

通過(guò)對(duì)各種氣體利用不同算法得到的JT系數(shù)與文獻(xiàn)[10]的實(shí)驗(yàn)數(shù)據(jù)比較的平均相對(duì)誤差可以看出：各種氣體采用RK方程計(jì)算JT系數(shù)均能獲得較高的精度。分別通過(guò)編程利用RK方程作出干氣密封常用工業(yè)氣體氫氣、氮?dú)狻⒖諝夂投趸紝?duì)應(yīng)的焦耳-湯姆遜系數(shù)曲線，如圖1所示。

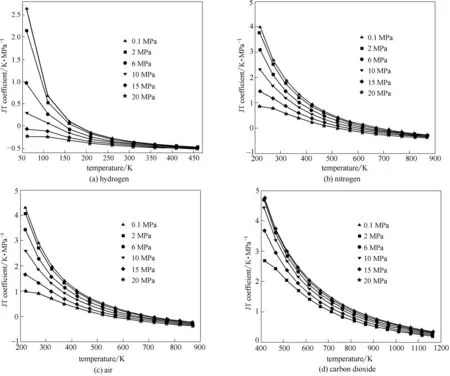
圖1 4種氣體的JT系數(shù)曲線

由圖1可以看出：4種氣體的JT系數(shù)均隨溫度和壓力的升高而降低，且變化幅度逐漸減小。根據(jù)相同溫度和壓力下不同氣體的JT系數(shù)比較，可判斷4種氣體的JT效應(yīng)的冷效果由強(qiáng)到弱依次為二氧化碳、空氣、氮?dú)夂蜌錃狻?/p>

2 焦耳-湯姆遜反轉(zhuǎn)曲線（JTIC）

對(duì)于實(shí)際氣體，隨著氣體壓力的升高，JT系數(shù)由大變小，甚至出現(xiàn)負(fù)值。JT系數(shù)從正值變到負(fù)值，必經(jīng)過(guò)JT系數(shù)等于零的點(diǎn)。當(dāng)JT系數(shù)為正值，即，發(fā)生致冷效應(yīng)；當(dāng)JT系數(shù)為負(fù)值，即，發(fā)生致熱效應(yīng)；當(dāng)JT系數(shù)為零，即，為理想氣體，既不致冷，也不致熱。可通過(guò)的點(diǎn)來(lái)判斷的正負(fù)，將一系列的點(diǎn)連接起來(lái)就形成一條曲線，稱為焦耳-湯姆遜反轉(zhuǎn)曲線（JTIC），即通過(guò)此曲線時(shí)，焦耳-湯姆遜效應(yīng)反 轉(zhuǎn)[17-20]。通過(guò)JTIC很容易判斷出實(shí)際氣體的致冷區(qū)域和致熱區(qū)域。在低壓側(cè)，即在JTIC內(nèi)側(cè)是致冷區(qū)域；在高壓側(cè)，即JTIC外側(cè)是致熱區(qū)域。令，由式（2）可以得到JTIC方程表達(dá)式。

聯(lián)合式（4）和式（22）化解得的方程為

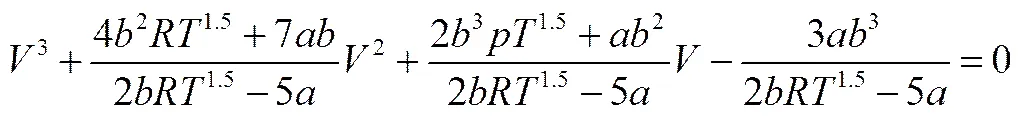
按照式（10）～式（12）求壓縮因子的方法將式（23）轉(zhuǎn)化為卡爾丹公式形式，并解出用表示氣體值的表達(dá)式為

其中

將式（24）代入式（4）得到溫度與壓力關(guān)系的JTIC方程表達(dá)式為

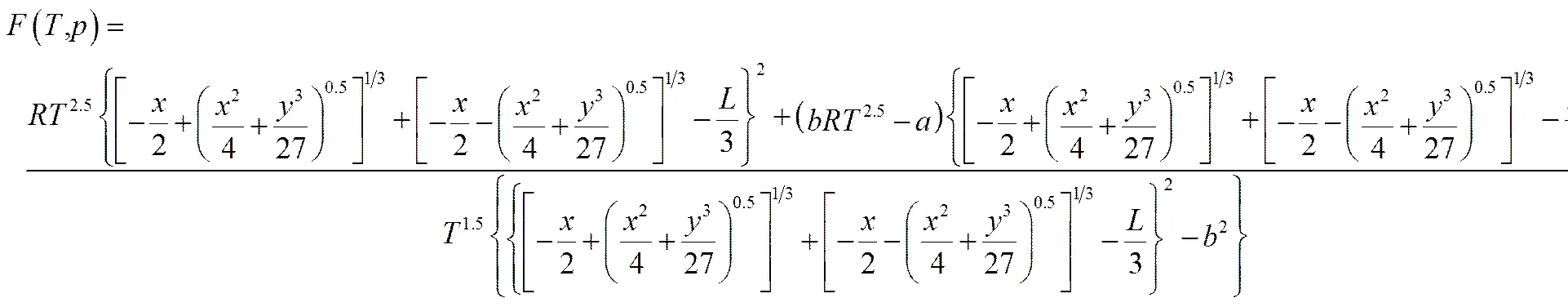
令(,)0，通過(guò)編程利用RK方程作出氫氣、氮?dú)狻⒖諝夂投趸紝?duì)應(yīng)的JTIC，如圖2所示。

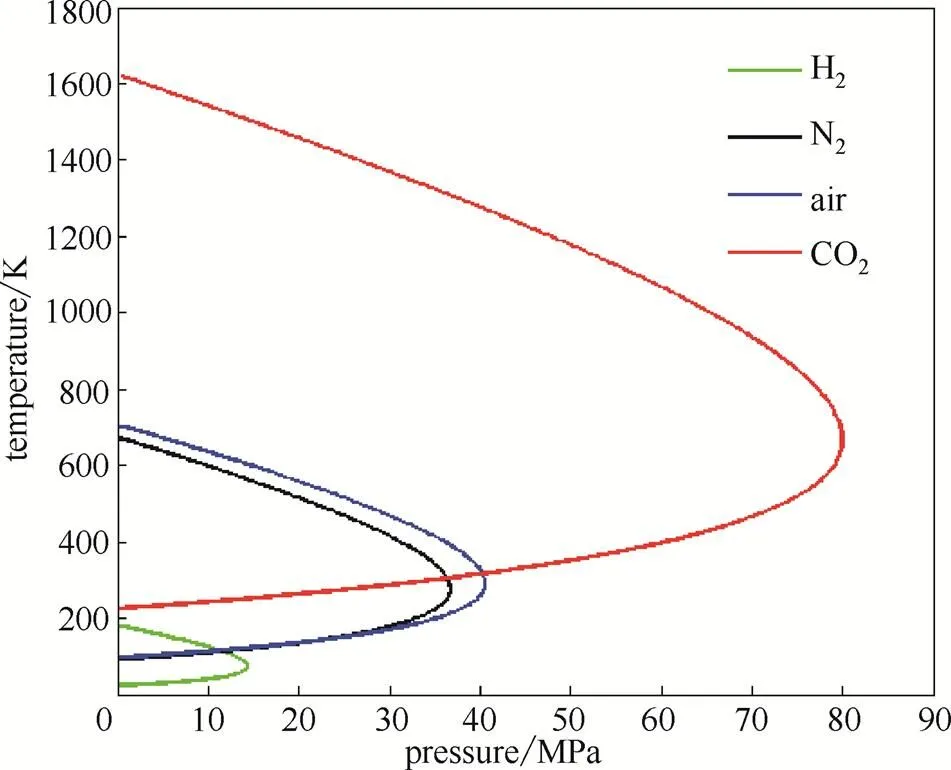
圖2 4種氣體的JT反轉(zhuǎn)曲線

由圖2可以清晰地看出：利用RK方程作出的4種氣體JT反轉(zhuǎn)曲線中，氫氣和二氧化碳的JT反轉(zhuǎn)曲線相差較大。二氧化碳反轉(zhuǎn)曲線的溫度范圍為200～1600 K，最高轉(zhuǎn)化壓力超過(guò)80 MPa，二氧化碳極易發(fā)生致冷效應(yīng)。而氫氣的最高轉(zhuǎn)化溫度低于200 K，氫氣只有在預(yù)冷到很低的溫度時(shí)，節(jié)流后才會(huì)發(fā)生致冷效應(yīng)。在常溫情況下，氫氣均發(fā)生致熱效應(yīng)。這在氫氣的常溫充裝過(guò)程中，會(huì)發(fā)生溫度升高現(xiàn)象，這正是氫氣焦耳-湯姆遜致熱效應(yīng)的表現(xiàn)[21]。各種氣體在反轉(zhuǎn)曲線上對(duì)應(yīng)的溫度和壓力工況，可視為理想氣體，不發(fā)生焦耳-湯姆遜效應(yīng)，或稱為焦耳-湯姆遜零效應(yīng)。但在干氣密封的實(shí)際運(yùn)行過(guò)程中，很難保證密封氣的溫度和壓力能穩(wěn)定在反轉(zhuǎn)曲線上，所以干氣密封很容易發(fā)生焦耳-湯姆遜致冷效應(yīng)或致熱效應(yīng)。一般壓力范圍內(nèi)的干氣密封，氫氣容易發(fā)生致熱效應(yīng)，而氮?dú)狻⒖諝夂投趸細(xì)怏w容易發(fā)生致冷效應(yīng)。

3 計(jì)算實(shí)例

3.1 JT效應(yīng)引起的溫差計(jì)算

考慮氣體通過(guò)干氣密封端面的焦耳-湯姆遜效應(yīng)時(shí)，將氣體通過(guò)干氣密封端面的過(guò)程視為等焓節(jié)流膨脹過(guò)程，僅考慮JT效應(yīng)引起的溫度變化，即溫差。其溫差ΔH的定義式如下[22]

聯(lián)合式（1）、式（4）、式（13）、式（18）和式（21）求得利用RK方程表示的JT系數(shù)

由于JT系數(shù)與壓力可近似為直線關(guān)系[23]，為了提高ΔH的計(jì)算精度，采用辛普森數(shù)值積分法可將式（26）的溫差ΔH的表達(dá)式轉(zhuǎn)化為

用高級(jí)程序語(yǔ)言編程計(jì)算在不同介質(zhì)溫度o和不同外部壓力o時(shí)溫差ΔH的變化情況。不考慮密封端面的具體結(jié)構(gòu)尺寸，僅考慮壓差的變化。選擇空氣作為密封介質(zhì)，環(huán)境壓力為i0.1013 MPa，外部壓力o為0.3～20 MPa，介質(zhì)溫度o為278～333 K。聯(lián)合式（28）和式（29）計(jì)算所得的密封端面內(nèi)外徑的溫差ΔH如表8所示。

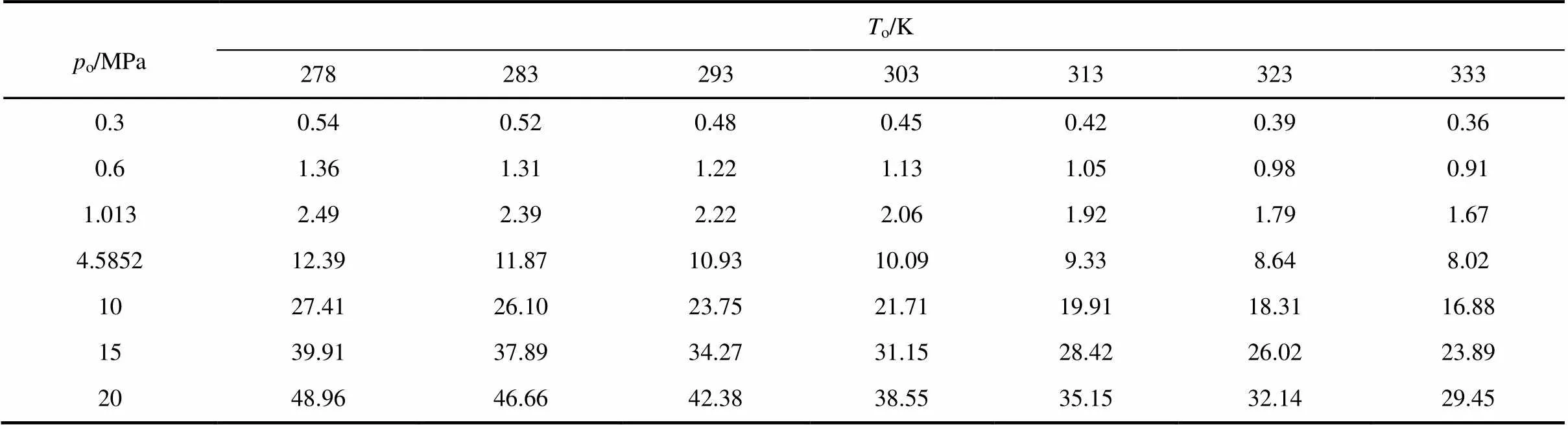
表8 不同溫度和壓力下空氣的溫差變化

表8計(jì)算結(jié)果的合理性，可由文獻(xiàn)[24]提供的案例得到支持。文獻(xiàn)[24]提供的案例為：空氣在293 K時(shí)，從1.013 MPa節(jié)流到0.1013 MPa，溫度可降低到290.7 K，即下降2.3 K。在相同情況下由式（22）編制程序計(jì)算的溫度下降2.22 K。兩者吻合。利用高級(jí)程序語(yǔ)言編制的程序，將表8中的密封介質(zhì)換成氮?dú)猓渌麉?shù)不變，計(jì)算密封端面內(nèi)外徑的溫差ΔH如表9所示。

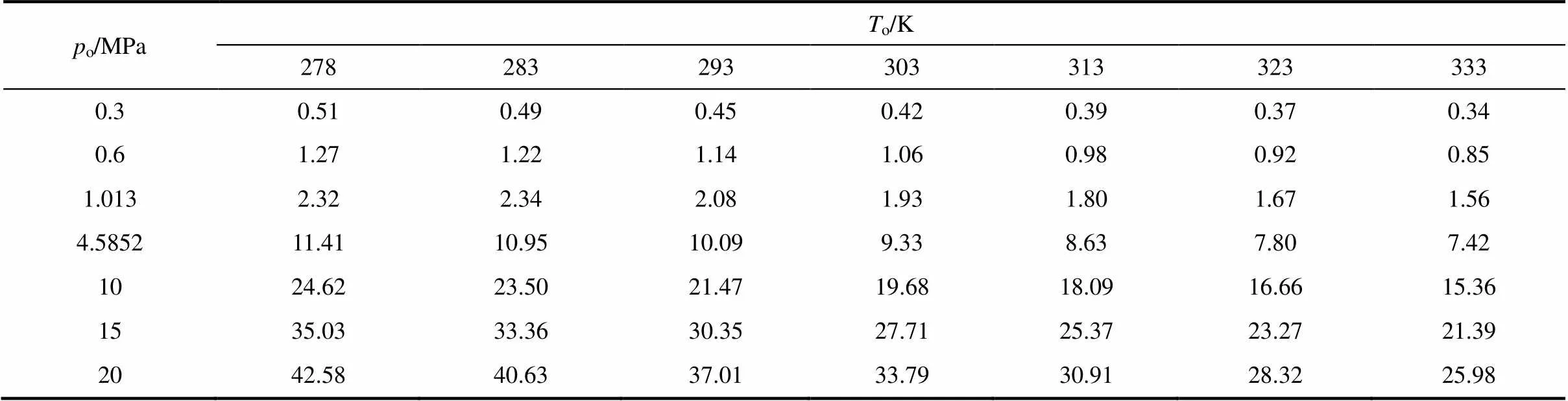
表9 不同溫度和壓力下氮?dú)獾臏夭钭兓?/p>

由表8和表9的數(shù)據(jù)可以看出，由于圖2中空氣和氮?dú)獾慕苟?湯姆遜系數(shù)曲線類似，且空氣的JT系數(shù)略高于氮?dú)猓谙嗤r下空氣的溫差均略大于氮?dú)狻烧叩臏夭钭兓哂邢嗤囊?guī)律，當(dāng)介質(zhì)溫度一定時(shí)，溫差隨外部壓力增大而增大。盡管JT系數(shù)隨壓力的增加而降低，但總的溫差仍隨壓力的增加而增加。只不過(guò)低壓區(qū)由于JT系數(shù)大對(duì)總體溫差的貢獻(xiàn)較大，而高壓區(qū)由于JT系數(shù)小，對(duì)總體溫差的貢獻(xiàn)較小。當(dāng)外部壓力一定時(shí)，溫差隨密封介質(zhì)溫度增大而減小，這是因?yàn)镴T系數(shù)隨溫度的增加而降低。外部壓力比介質(zhì)溫度對(duì)溫差的影響更大。干氣密封封氣介質(zhì)的實(shí)際氣體焦耳-湯姆遜效應(yīng)能引起較大的溫度變化，只有在壓力較小時(shí)方可不用考慮。

3.2 空氣含水的溫差計(jì)算

考慮到空氣含有水蒸氣的情況，作出不同濕度下的空氣對(duì)應(yīng)的露點(diǎn)曲線，同時(shí)作出某一溫度和壓力下的膨脹線和JT效應(yīng)引起的溫降曲線。

將濕空氣看為水和干空氣的混合物，其安托因參數(shù)見(jiàn)表10[25]。利用安托因方程式（30）便可以計(jì)算出水的飽和蒸氣壓[26]。

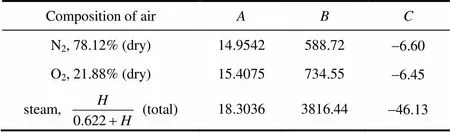
表10 安托因參數(shù)[25]

對(duì)于濕空氣來(lái)說(shuō)，其相對(duì)濕度和濕度的表達(dá)式分別為

密封氣流過(guò)密封端面、孔板等組件時(shí)，假設(shè)發(fā)生不可逆膨脹過(guò)程，其壓力溫度關(guān)系符合過(guò)程方程[27]

式中，1、1為膨脹初始?jí)毫统跏紲囟龋?、2為膨脹后的壓力和溫度。為過(guò)程指數(shù)，絕熱膨脹時(shí)，過(guò)程指數(shù)等于絕熱指數(shù)，則。

利用高級(jí)程序語(yǔ)言編制程序，作出不同濕度空氣的露點(diǎn)曲線，并在同一個(gè)圖中作出初始溫度和壓力為373.15 K和10 MPa的膨脹線以及JT效應(yīng)引起的溫降線，同時(shí)將絕熱膨脹和JT效應(yīng)組合，作出兩者共同作用引起的溫降曲線如圖3所示。

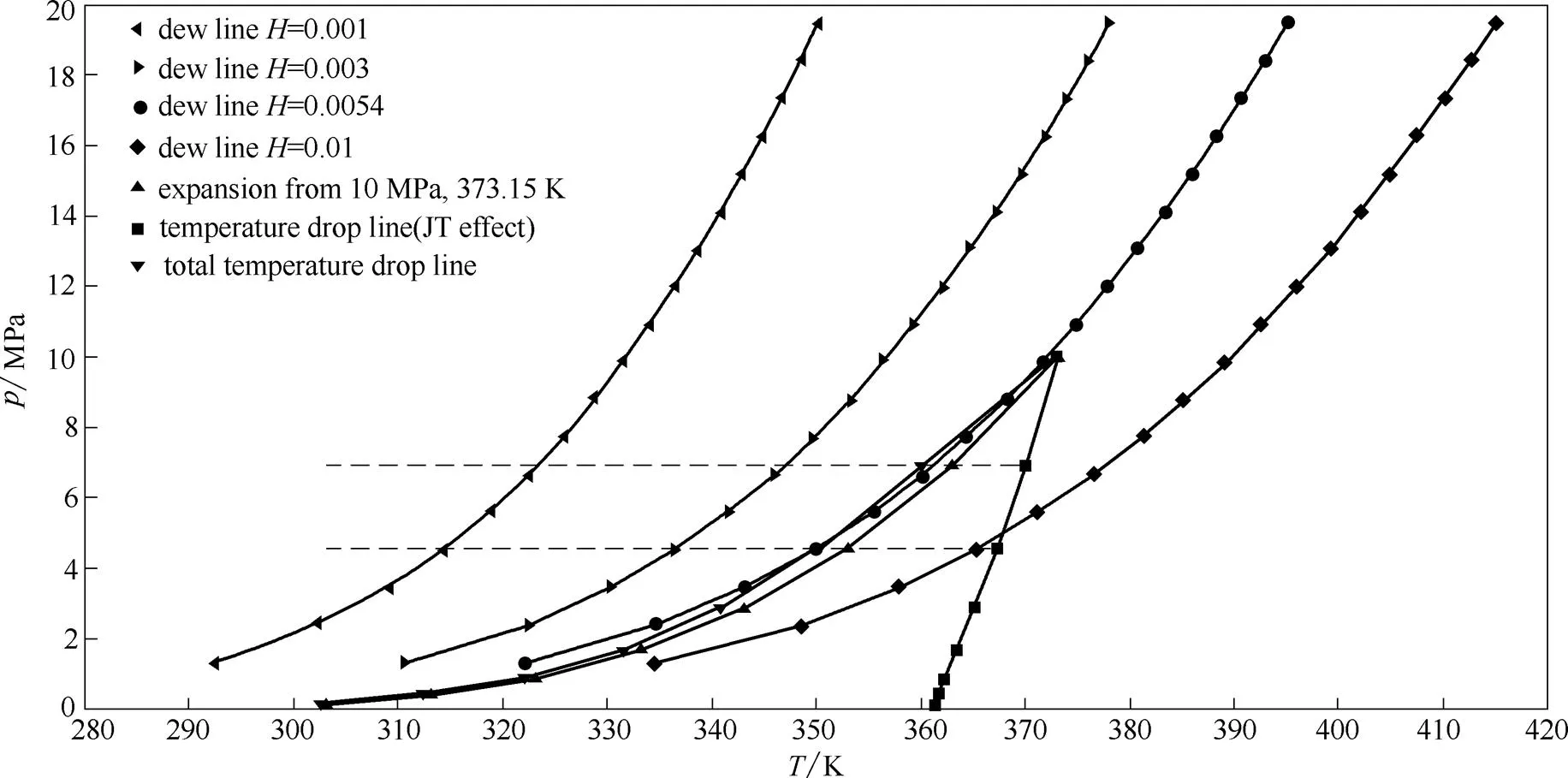
圖3 露點(diǎn)線、膨脹線和JT效應(yīng)引起的溫降線

4 結(jié) 論

（1）實(shí)際氣體的焦耳-湯姆遜效應(yīng)，對(duì)干氣密封的節(jié)流環(huán)節(jié)會(huì)產(chǎn)生重要影響。常溫條件下，氫氣發(fā)生致熱效應(yīng)，而氮?dú)狻⒖諝狻⒍趸細(xì)怏w發(fā)生致冷效應(yīng)。

（2）分析干氣密封的焦耳-湯姆遜效應(yīng)時(shí)，采用RK狀態(tài)方程計(jì)算壓縮因子和比定壓熱容,real較為合理。

（3）獲得了一種計(jì)算焦耳-湯姆遜效應(yīng)反轉(zhuǎn)曲線的方法和程序。

（4）獲得了一種考慮焦耳-湯姆遜效應(yīng)確定節(jié)流溫差的計(jì)算方法和程序。

References

[1] 鐘桂香, 羅瀟, 郗祥遠(yuǎn). 干氣密封失效原因分析與有效性措施 [J]. 油氣儲(chǔ)運(yùn), 2014, 33 (3): 335-339. DOI: 10. 6047/j.issn.1000- 8241.2014.03.026.
ZHONG G X, LU X, XI X Y. Failure analysis and effective measures in the dry gas seal [J]. Oil & Gas Storage and Transportation, 2014, 33 (3): 335-339. DOI: 10.6047/j.issn.1000-8241.2014.03.026.

[2] 馬麗芳. 干氣密封氣析出液處理 [J]. 蘭州石化職業(yè)技術(shù)學(xué)院學(xué)報(bào), 2010, 10 (4): 7-9.
MA L F. Processing for separation fluid of dry gas seal gas [J]. Journal of Lanzhou Petrochemical College of Technology, 2010, 10 (4): 7-9.

[3] 許靜, 彭旭東, 白少先, 等. 氣體熱黏效應(yīng)對(duì)干氣密封性能影響的數(shù)值分析 [J]. 上海交通大學(xué)學(xué)報(bào), 2012, 46 (5): 722-728.
XU J, PENG X D, BAI S X,. Numerical analysis of gas thermal viscosity effect on performance of a spiral-groove gas face seal [J]. Journal of Shanghai Jiaotong University, 2012, 46 (5): 722-728.

[4] 許靜, 彭旭東, 白少先, 等. 端面微尺度效應(yīng)和熱黏效應(yīng)對(duì)干氣密封性能的影響 [J]. 化工學(xué)報(bào), 2013, 64 (9): 3291-3330. DOI: 10.3969/j.issn.0438-1157.2013.09.030.
XU J, PENG X D, BAI S X,. Effect of surface micro-scale and thermal viscosity on sealing performance of spiral-groove dry gas seal [J]. CIESC Journal, 2013, 64 (9): 3291-3330. DOI: 10.3969/j.issn.0438- 1157.2013.09.030.

[5] 丁雪興, 劉勇, 張偉政, 等. 螺旋槽干氣密封微尺度氣膜的溫度場(chǎng)計(jì)算 [J]. 化工學(xué)報(bào), 2014, 65 (4): 1353-1358. DOI: 10.3969/j.issn.0438- 1157.2014.04.027.
DING X X, LIU Y, ZHANG W Z,. Calculation of temperature filed of micro-scale gas film in spiral groove dry gas seal [J]. CIESC Journal, 2014, 65 (4): 1353-1352. DOI: 10.3969/j.issn.0438- 1157.2014.04.027.

[6] 宋鵬云, 胡曉鵬, 許恒杰, 等. 實(shí)際氣體對(duì)T槽干氣密封動(dòng)態(tài)特性的影響 [J]. 化工學(xué)報(bào), 2014, 65 (4): 1344-1352. DOI: 10.3969/ j.issn.0438-1157.2014.04.026.
SONG P Y, HU X P, XU H J,. Effect of real gas on dynamic T-groove dry gas seal [J]. CIESC Journal, 2014, 65 (4): 1344-1352. DOI: 10.3969/j.issn.0438-1157.2014.04.026.

[7] 朱自強(qiáng), 吳有庭. 化工熱力學(xué) [M]. 北京: 化學(xué)工業(yè)出版社, 2010: 126-147.
ZHU Z Q, WU Y T. Chemical Engineering Thermodynamics [M]. Beijing: Chemical Industry Press, 2010: 126-147.

[8] 李西平, 司云森.物理化學(xué) [M]. 昆明: 云南大學(xué)出版社, 2006: 40-41.
LI X P, SI Y S. Physical Chemical [M]. Kunming: Yunnan University Press, 2006: 40-41.

[9] 王竹溪. 熱力學(xué) [M]. 2版. 北京: 北京大學(xué)出版社, 2014: 67-72.
WANG Z X. Thermodynamics [M].2nd ed. Beijing: Peking University Press, 2014: 67-72.

[10] PERRY R H. Perry’s Chemical Engineers’ Handbook [M]. 7th ed. New York: McGraw-Hill, 1997: 132-182.

[11] 陳鐘秀, 顧燕飛, 胡望明. 化工熱力學(xué) [M]. 3版. 北京: 化學(xué)工業(yè)出版社, 2011: 184-185.
CHEN Z X, GU Y F, HU W M. Chemical Engineering Thermodynamics [M]. 3rd ed. Beijing: Chemical Industry Press, 2011: 184-185.

[12] 曾彪, 張旭, 鮑謙. 濕空氣絕熱節(jié)流系數(shù)計(jì)算及討論 [J]. 暖通空調(diào), 2011, 41 (9): 115-119.
ZENG B, ZHANG X, BAO Q,. Calculation and discussion of adiabatic throttling coefficient for moist air [J]. Heating Ventilating and Air Conditioning, 2011, 41 (9): 115-119.

[13] 馬沛生, 宣愛(ài)國(guó), 周彩榮，等. 化工熱力學(xué) [M]. 北京: 化學(xué)工業(yè)出版社, 2009: 40-42.
MA P S, XUAN A G, ZHOU C R,. Chemical Engineering Thermodynamics [M]. Beijing: Chemical Industry Press, 2009: 40-42.

[14] 程陽(yáng), 李東升, 胡佳成. 空氣靜壓潤(rùn)滑焦耳-湯姆遜系數(shù)的計(jì)算方法 [J]. 潤(rùn)滑與密封, 2014, 39 (6): 103-107.
CHEN Y, LI D S, HU J C. The calculation method of Joule-Thomson coefficient in air aerostatic lubrication [J]. Lubrication Engineering, 2014, 39 (6): 103-107.

[15] 清華大學(xué). 數(shù)學(xué)手冊(cè) [M]. 北京: 高等教育出版社, 2004: 88-89.
Tsinghua University. Mathematics Handbook [M]. Beijing: Higher Education Press, 2004: 88-89.

[16] 石玉冰. 真實(shí)氣體等壓熱容的關(guān)聯(lián) [J]. 化肥設(shè)計(jì), 2010, 48 (3): 11-13.
SHI Y B. Correlation of heat capacity at constant pressure for real gas [J].Chemical Fertilizer Design, 2010, 48 (3): 11-13.

[17] MATIN N S, HAGHIGHI B. Calculation of the Joule-Thomson inversion curves from cubic equation of state [J]. Fluid Equilibria, 2000, 175 (1): 273-284. DOI: 10.1016/S0378-3812(00)00443.

[18] WISNIAK J, AVRAHAM H. On the Joule-Thomson integral inversion curves [J]. Thermochimica Acta, 1996, 286 (1): 33-40.

[19] MAYTAL B Z, SHAVIT A. On the Joule-Thomson integral inversion curves of quantum gases [J]. Cryogenics, 1997, 37 (1): 33-38. DOI: 10. 1016/S0011-2275(96)00094 -X.

[20] COLINA C M, OLIVERA-FUENTS C. Prediction of the Joule-Thomson inversion curve of air from cubic equations of state [J]. Cryogenics, 1998, 8 (7): 721-728. DOI: 10.1016/S0011- 2275(98)00036-8.

[21] 劉延雷. 高壓氫氣快充溫升控制及泄漏擴(kuò)散規(guī)律研究 [D]. 杭州: 浙江大學(xué), 2009.
LIU Y L. Investigating on control of temperature rise in fast filling of high pressure hydrogen and diffusion due to its leakage [D]. Hangzhou: Zhejiang University, 2009.

[22] 胡登輝. 非理想氣體節(jié)流過(guò)程熱力學(xué)研究及實(shí)踐應(yīng)用 [D]. 大慶: 東北石油大學(xué), 2011.
HU D H. Non-ideal gas throttling process thermodynamic analysis and applied research [D]. Daqing: Northeast Petroleum University. 2011.

[23] 劉豐, 李晶晶. 基于HYSYS的焦耳-湯姆遜效應(yīng)實(shí)驗(yàn)裝置設(shè)計(jì)與模擬分析 [J]. 廣州化工, 2014, 42 (14): 164-166.
LIU F, LI J J. Experimental design and simulation of Joule-Thomson effect based on HYSYS [J]. Guangzhou Chemical Industry, 2014, 42 (14): 164-166.

[24] 高光華, 童景山. 化工熱力學(xué) [M]. 北京: 清華大學(xué)出版社, 2007: 204-207.
GAO G H, TONG J S. Chemical Engineering Thermodynamics [M]. Beijing: Tsinghua University Press, 2009: 204-207.

[25] 馬沛生, 夏淑倩, 夏清. 化工物性數(shù)據(jù)簡(jiǎn)明手冊(cè) [M]. 北京: 化學(xué)工業(yè)出版社, 2013: 17-18.
MA P S, XIA S Q, XIA Q. Chemical Property Data Concise Guide [M]. Beijing: Chemical Industry Press, 2013: 17-18.

[26] 郭天明. 多元汽-液平衡和精餾 [M]. 北京: 化學(xué)工業(yè)出版社, 2002: 161-300.
GUO T M. Diverse Vapor-Liquid Equilibrium and Distillation [M]. Beijing: Chemical Industry Press, 2002: 161-300.

[27] 李云, 姜培正. 過(guò)程流體機(jī)械 [M]. 2版. 北京: 化學(xué)工業(yè)出版社, 2008: 13-21.
LI Y, JIANG P Z. Process Fluid Machinery [M]. 2nd ed. Beijing: Chemical Industry Press, 2008: 13-21.

Analysis of Joule-Thomson effect of real gas system sealed by dry gas

DENG Chengxiang, SONG Pengyun, MA Ailin

(Faculty of Chemical Engineering, Kunming University of Science and Technology, Kunming 650500, Yunnan, China)

In a system sealed by dry gas, the Joule-Thomson (JT) effect occurs when the gas flows through the components of filters, valves, orifices and end faces, which may cause the temperature drop of sealing gas, even the appearance of liquid condensation. Generally, the Joule-Thomson effect is represented by Joule-Thomson coefficient. As to the hydrogen, nitrogen, air and carbon dioxide, which are often encountered for the cases of sealing by dry gas, the corresponding Joule-Thomson (JT) coefficients were calculated by four classical equations of state (EOS) of VDW, RK, SRK and PR. Subsequently, those calculated coefficients are compared with the experimental data in the literatures. The JT coefficient curves and Joule-Thomson inversion curves (JTIC) were plotted using the optimal equation of state. As to air and nitrogen through the end faces of dry sealing gas, the gas temperature drops caused by JT effect were calculated by applying the computer program. It shows that the Joule-Thomson effect of real gas, which have important influence on the throttle of dry sealing gas. At room temperature, hydrogen showed exothermic effect, while nitrogen, air and carbon dioxide endothermic (cooling) effect. The corresponding Joule-Thomson (JT) coefficients were calculated by the four classical EOS, the average relative error and maximum relative error of RK equation were the minimum, less than 4% and 10%, respectively. The JT effect of real gas causes large temperature difference in the dry sealing gas, of which the gas pressure more influences on the temperature drop than the gas temperature does. When the pressure is small, the temperature drop by the JT effect can be negligible.

dry gas seal; real gas; equation of state; Joule-Thomson coefficient; inversion curve

supported by the National Natural Science Foundation of China (51465026).

date: 2015-12-14.

Prof. SONG Pengyun, songpengyunkm@ ina.com

TB 42；TQ 031.1

A

0438—1157（2016）09—3833—10

10.11949/j.issn.0438-1157.20151892

國(guó)家自然科學(xué)基金項(xiàng)目(51465026)。

2015-12-14收到初稿，2016-06-23收到修改稿。

聯(lián)系人：宋鵬云。第一作者：鄧成香（1989—），男，碩士研究生。