考慮風向角的地面光伏陣列風壓折減特性研究

■ 姜濤 牛斌

中國建筑設計研究院（集團）中國建筑設計咨詢有限公司

考慮風向角的地面光伏陣列風壓折減特性研究

■ 姜濤 牛斌*

中國建筑設計研究院（集團）中國建筑設計咨詢有限公司

針對地面光伏電站流場不均勻且各陣列所受風壓復雜的特性，采用CFD方法分析不同風向下多排陣列風載荷的變化情況，并討論最不利條件下陣列間距對折減特性的影響。結果表明：當來流風向為北風和南風時，風載荷折減效應最明顯，隨著風向角向橫向靠近，折減效應趨于平緩，最大載荷也逐漸減小；在地面光伏電站中，受風載荷影響最大的為外圍光伏結構，在陣列排布及結構設計時應基于流體力學計算結果考慮風壓折減，劃分風載荷區域。

光伏陣列；風向角；風載荷；凈力系數；折減特性

0　引言

隨著不可再生能源儲備的減少及清潔能源需求的增加，綠色建筑和低碳節能理念越來越受到重視，促進了光伏產業的興起。而強風下光伏陣列所受載荷是整個光伏系統設計與建造的關鍵之一，因而必須研究強風對光伏陣列風載荷的影響規律，以作為光伏支撐結構設計的依據。

目前關于光伏電站陣列風載荷的研究主要有2種方法：風洞實驗［1-3］和理論計算。理論計算分為3種方法：一是在整個風荷載區域采用單一結構體型系數的工程算法；二是基于工程算法改進，考慮光伏陣列所受風壓不均勻的半經驗法；三是基于CFD方法的數值計算。由于光伏陣列不同區域所受風壓不同、陣列受力不均勻等特點，傳統的工程算法和半經驗法對風載荷的計算會造成工程設計中不必要的浪費。基于CFD方法的數值計算結果則與實際更相符，但對計算條件要求較高，計算時間也較長。目前基于CFD方法的光伏風載荷計算國內公開發表的文獻較少，國外學者對光伏結構受風力影響較為重視，并應用數值模擬開展了相關研究。Banks［4］率先提出光伏陣列風壓的計算機模擬會直接影響未來光伏產業的發展。Chung等［5］對光伏結構所受風吸力及壓力系數進行了研究。Bitsuamlak等［6］采用流體力學計算軟件對光伏陣列進行風載模擬。Yu［7］基于CFD方法采用不同湍流模型模擬穩態條件下光伏陣列在強風下的受力情況，通過與現場實測結果對照驗證了計算機模擬的可行性和有效性。但上述文章均未考慮光伏陣列間的折減效應。Warsido等［8］以陣列間距為參數研究了其對光伏結構風壓的影響。V?sie?等［9］在2012年對有無女兒墻的平屋頂上安裝的光伏結構進行數值模擬分析，文章基于計算機模擬結果對結構設計提出指導。但上述文章均未考慮不同風向角下結構風載荷的變化規律。如何運用計算流體力學方法刻畫光伏陣列風壓特性，并將其應用于光伏結構的風載評估，為光伏陣列的結構設計提供指導，尚缺少系統的研究。

本文應用CFD方法研究地面光伏陣列的風壓特性，通過分析不同來流風向角及不同陣列間距下流場及光伏陣列氣動力特性，對光伏陣列及結構進行風載荷評估，為光伏結構設計提供技術指導。

1　理論與方法

本文首先計算強風下光伏陣列流場域的定常解，之后以定常解為初始條件求得光伏陣列流場域的非定常解。

對于定常解，流場求解方程采用基于Favre平均的N-S方程，其數學描述如下［10］：

對于不可壓縮流動，密度ρ不隨坐標變化。為保證上述方程封閉，選用（SST）k-ω雙方程湍流模型，其中湍動能k和耗散率ω由式（4）和式（5）確定。

式中，F1為調配函數； vt為湍流渦粘性系數，由式（6）確定。

該模型中各變量的物理意義及求解可見文獻［11］。

通過給定風速、流場域及物理模型相關參數，求解流體控制方程，得到流體區域的穩態場解，即可獲得光伏陣列壁面的壓力分布，繼而求得光伏陣列穩態條件下的風載荷大小。

對于非定常解，理論模型采用大渦模擬模型。對N-S方程組進行空間濾波，得到大渦模擬的基本方程：

為保證上述方程封閉，采用Boussinesq假設，亞格子尺度應力由式（9）計算：

通過給定入口風速邊界條件，以穩態解為初始條件，求解流體控制方程，得到流體區域的流場分布，即可獲得光伏陣列所受風壓情況，繼而積分可求得各陣列所受風載荷的大小及其折減系數。

2　計算模型與參數

計算模型選用我國某地面光伏電站標準光伏組件，光伏陣列幾何尺寸：20 m×0.1 m×3.5 m，安裝傾角為30°，底部距地面高0.5 m，各陣列間距為5.8 m；選用來流風向角Angle為計算參數，取值范圍：Angle=0°+n×30°，n取值范圍為0～6。Angle取值、陣列編號及坐標如圖1所示。

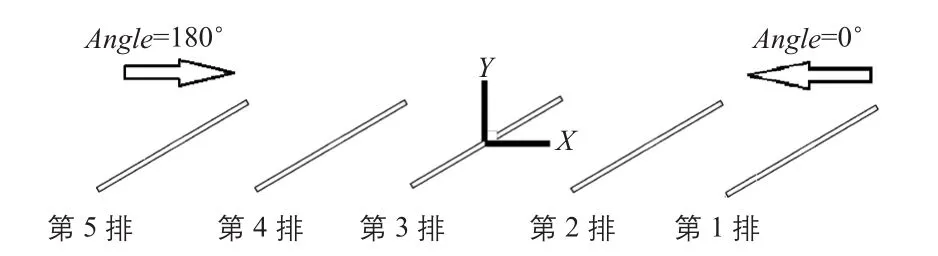
圖1　風向角取值及坐標方向示意圖

計算5排陣列，流體幾何模型大小為：100 m×10 m×55 m，采用有限體積法離散控制方程，非定常計算時間40 s。為保證計算精度，靠近結構壁面區域網格逐漸加密。壁面邊界層為10層，最小尺寸0.001 m，增長系數1.2，單元總數125萬。計算模型及邊界層附近網格劃分見圖2。來流參數：v=30 m/s，P=1.01×105Pa，Re=2.5×106，T=288 K，下游流出為壓力邊界，相對壓力為0；底部及光伏陣列為無滑移邊界。

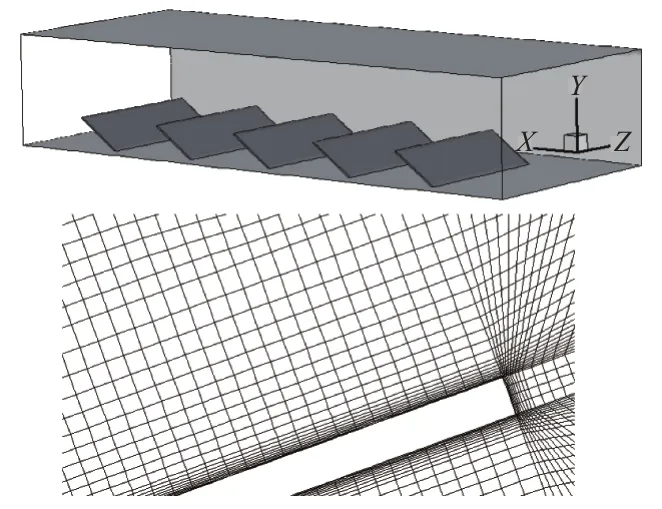
圖2　計算模型及壁面附近網格劃分

3　計算結果和分析

3.1流場計算結果

圖3為Angle=0°時對稱面流線分布圖。由圖3可得，來流進入光伏陣列中，繞過首排光伏陣列后在板后形成一主漩渦，其尺度與Re和光伏陣列傾角有關；同時由于剪切層分離后再附，產生了一定的回流，在光伏陣列間也會有局部渦的存在；中心大渦與局部渦方向相反，這些渦都會對陣列產生一定吸力。圖4為Angle=180°時對稱面流線分布圖，由于板傾斜方向與來流方向一致，主漩渦位置在第1、2排之間，各排間均有一尺度較大的局部渦。渦旋結構的相互影響使流動變得十分復雜，不同排的光伏陣列，乃至同一排光伏陣列的不同位置所受風壓均不同。證明了光伏陣列中采用CFD方法預測風載的必要性。

圖3　Angle=0°時對稱面流線分布

圖4　Angle=180°時對稱面流線分布

3.2光伏陣列氣動力特性

由流場結果可得光伏陣列的氣動力分布情況，圖5為不同來流風向角下光伏陣列迎風、背風面壓力分布云圖。由圖5a可得，Angle=0°時第1排迎風處風壓最大（585 Pa），由于板間渦旋的存在，第1排迎風面處為正壓、背風面為負壓，兩方面作用使得陣列承受掀起力，其余順風向組件所受氣動力均有不同程度的折減。圖5b和圖5c分別為Angle=60°和120°時光伏陣列壁面壓力分布云圖，由圖可知，因板間遮擋而引起的折減效應較為明顯。由圖5d可知，Angle=180°時第5排迎風處風壓最大（539 Pa），陣列承受下壓力，其余各排由于遮擋作用附近風壓相對較小。

圖5　光伏陣列壁面壓力云圖

3.3光伏陣列風載荷計算

將壁面壓力值以參考動壓為基準做歸一化處理，可得光伏陣列無量綱壓力系數：

式中，P為光伏陣列壁面壓力；ρa為空氣密度；為參考高度下的平均風速。定義凈壓力系數為迎風面與背風面壓力系數之差，則其時間歷程ΔCPN（t）如式（11）所示：

式中，下標N、W、L分別表示凈壓力、迎風面和背風面。對其進行面積分得到垂直壁面方向的總凈力：

式中，m、n分別為迎風面、背風面上網格數量；AWi、ALi分別為CPWi、CPLi對應的壁面單元面積。通過歸一化處理將FN（t）轉為如下無量綱形式：

式中，B、L分別為光伏板的寬度和長度。

至此，在光伏結構設計中起關鍵作用的風載荷計算轉變為凈力系數CFN（t）的計算和分析。

圖6為光伏陣列各排CFN隨風向角的變化曲線。由圖6可知，Angle=0°時第1排的CFN為最大值（0.93），光伏陣列受掀起力最大；Angle=180°時第5排的為最小值（-0.81），光伏陣列受下壓力最大；各排CFN均以Angle=90°為拐點，由掀起力過渡至下壓力。

圖7給出了Angle=0°～90°和Angle=90°～180°時各風向角下CFN在不同陣列間的變化曲線。由圖可知，當Angle=0°和Angle=90°時，陣列迎風向的折減最明顯，分別為12.8%和8.4%，后續陣列所受載荷有所增加但變化較小；隨著風向角向90°靠近，最大載荷逐漸減小，曲線趨于平緩，折減效應也逐漸減小。由上述分析可得，光伏陣列排布時，受風載荷影響最大的為外圍光伏結構，其余陣列受首排保護受力較小。在大型地面光伏電站設計中應劃分風載荷區域，使其更具有經濟合理性。

圖6　各陣列CFN隨風向角變化曲線

圖7　各風向角下CFN在不同陣列間的變化曲線

此外，針對光伏陣列承受風壓最大（北風，Angle=0°）的最不利情況，對不同光伏陣列間距下的風壓折減特性進行了分析。以間距為計算參數，取值范圍為4.76 m+n×0.5 m，n取0～7，得到不同間隔下光伏陣列各排CFN結果見表1。由表1可知，在間距較小（4.76～5.76 m）時，CFN負值出現在第4排；間距較大（7.26～8.26 m）時，負值在第3排。這是因為整體渦的位置與雷諾數相關，渦心與首排板距離基本不變，隨著板間距的增大，整體渦由第3排與第4排之間轉至第2排與第3排之間，而相應板后側的局部渦強度不及整體渦（參考圖3），因此光伏陣列受整體渦吸引作用較大，凈力系數的弱負值由第4排轉至第3排。但折減整體趨勢基本相同。

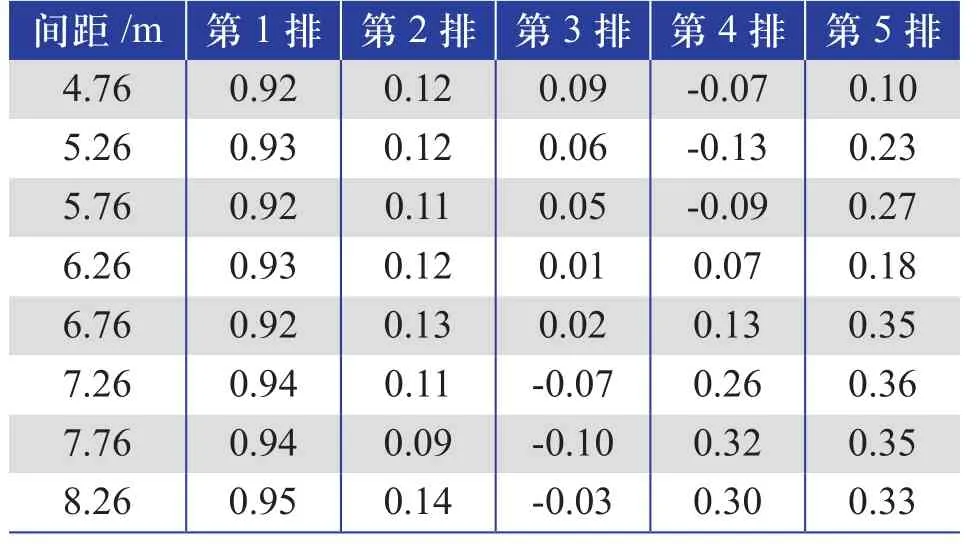
表1　不同間隔下光伏陣列各排CFN計算結果

由于中心渦位置的相對固定性及不同間距對首排風載影響較小，衰減趨勢相對變化不大，另外受光伏電站場地對間距的限制及成本影響等，研究陣列排布間距對風載影響的意義并不大。不同間距下的計算從側面證明了風載荷折減效應的通用性。

4　結論

本文采用CFD方法研究了地面光伏陣列的風壓折減特性。通過分析不同風向角和不同間距下流場及光伏陣列的氣動特性，說明了基于CFD計算結果進行結構設計的必要性。研究表明：在地面電站陣列排布中，當來流風向為北風和南風時，風載荷折減效應最明顯；隨著風向角向橫向靠近，折減效應趨于平緩，但最大載荷也逐漸減小。考慮到光伏陣列排布時，受風載荷影響最大的為外圍光伏結構，提出在光伏陣列排布及結構設計時基于CFD計算結果考慮風壓折減，劃分風載荷區域，節約成本。

［1］Pratt R N， Kopp G A. Velocity measurements around lowprofile， tilted， solar arrays mounted on large flat-roofs， for wall normal wind directions［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2013， 123， Part A: 226-238.

［2］Kopp G A， Farquhar S， Morrison M J. Aerodynamic mechanisms for wind loads on tilted， roof-mounted， solar arrays［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2012，111: 40-52.

［3］Abiola-Ogedengbe A. Experimental investigation of wind effect on solar panels［D］. Canada: University of Western Ontario， 2013.

［4］Banks D. How wind load studies will impact the solar industry ［EB/OL］. https://ases.conference-services.net/resources/252/2859/ pdf/SOLAR2012_0419_full%20paper.pdf.

［5］Chung K， Chang K， Liu Y. Reduction of wind uplift of a solar collector model［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2008， 96（8-9）: 1294-1306.

［6］Bitsuamlak G， Dagnew A， Erwin J. Evaluation of wind loads on solar panel modules using CFD［A］. 5th International Symposium on Computational Wind Engineering （CWE2010）［C］， Chapel Hill，North Carolina， USA， 2010.

［7］Yu Y. Numerical simulation of wind load on roof mounted solar panels［D］. Canada: University of Western Ontario， 2012

［8］Warsido W P， Bitsuamlak G T， Barata J， et al. Influence of spacing parameters on the wind loading of solar array［J］. Journal of Fluids and Structures， 2014， 48: 295-315.

［9］V?sie? G， Axinte E， Teleman E C. Numerical simulation of wind action on solar panel placed on flat roofs with and without parapet［J］. Bulletin of the Politehnic Institute of Iasi - Construction and Architecture， 2012， 58（1）: 139-155.

［10］Biswas G， Eswaran V. Turbulent flows:Fundamentals，experiments and modeling［M］. America: CRC Press， 2002.

［11］Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications［J］. AIAA Journal， 1994， 32（8）: 1598-1605.

2015-05-28

牛斌（1989—），男，工程師、助理研究員，主要從事光伏電站風載荷預測、結構設計及發電效率優化方面的研究。niubin@cadg.cn